General Bounds for Maximum Mean Discrepancy Statistics

HE Yulin(何玉林),HUANG Defa(黃德發(fā))DAI Dexin(戴德鑫),HUANG Zhexue(黃哲學(xué))

(College of Computer Science & Software Engineering,Shenzhen University,Shenzhen 518060,China)

Abstract: The classical maximum mean discrepancy statistics,i.e.,MMDb(F,X,Y)and MMD2u(F,X,Y),to test whether two samples X = {x1,x2,··· ,xm} and Y = {y1,y2,··· ,yn} are drawn from the different distributions p and q.MMDb and MMD2u are two very useful and effective statistics of which the bounds are derived based on the assumption of m = n.This paper relaxes this assumption and provides the general bounds for these two statistics statistics MMDb and MMD2u.The derived results show that the traditional bounds derived in previous study are the special cases of our general bounds.

Key words: Two-sample test;Maximum mean discrepancy (MMD);Reproducing kernel Hilbert space (RKHS);McDiarmid’s inequality

1.Two MMD Statistics MMDb and MMD2u

In order to determine how to test the difference between two distributionspandqbased on the independent and identical samplesX={x1,x2,··· ,xm}andY={y1,y2,··· ,yn}drawn from them,wheremandnare the numbers of sample belonging toXandY,respectively.Gretton,et al.[1]designed two MMDband MMD2ubased on the maximum mean discrepancy(MMD)principle,whereFis a class of smooth functions in a characteristic reproducing kernel Hilbert space (RKHS)[2].MMDband MMD2uare the generalizations ofL2statistic[3].The calculations of MMDband MMD2uwere provided as follows in [1],respectively:

and

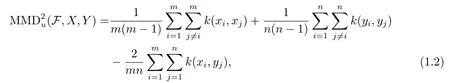
wherek(,)is a RKHS kernel function.

2.Traditional Bounds of MMDb and MMD2u When m=n

Assume 0≤k(·,·)≤K,whereKis the upper bound of kernel function.Corollary 9 and Corollary 11 in [1] gave the bounds of MMDband MMD2ubased on the assumption ofm=n.

Corollary 1[1]A hypothesis test of levelαfor the null hypothesis has the acceptance region

Corollary 2[1]A hypothesis test of levelαfor the null hypothesis has the acceptance region

3.General Bounds of MMDb and MMD2u When mn

Eq.(2.1)and Eq.(2.2)provide the useful and effective statistics for testingp=q.However,the above-mentioned bounds of MMDband MMD2uare derived based on the assumptionm=n.In this section,we relax this assumption and derive the more general bounds for MMDband MMD2u.

Corollary 3When,a hypothesis test of levelαfor the null hypothesisp=qhas the acceptance region

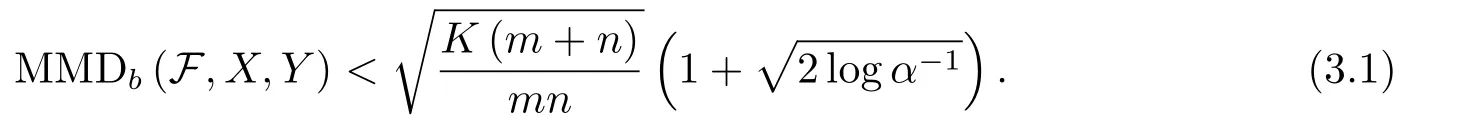
ProofWhenp=qandmn,we get

According to Theorem 7 in [1],we let

Combining Eq.(3.2)and Eq.(3.3),the McDiarmid’s inequality[4]

formnis yielded.In Eq.(3.3),we derive

and then the bound

is obtained.This completes the proof.

Corollary 4Whenmn,a hypothesis test of levelαfor the null hypothesisp=qhas the acceptance region

ProofAccording to the definition of MMD2u(F,X,Y)in Eq.(1.2),we calculate

Then,we derive

and

Based on the McDiarmid’s inequality[4],we get

and then the bound of MMD2u(F,X,Y)is obtained for the null hypothesisp=q.This completes the proof.

We can find that the bounds of MMDb(F,X,Y)and MMD2u(F,X,Y)whenm=nare the special cases of Eq.(3.1)and Eq.(3.7),i.e.,

4.Conclusions and Future Works

This paper relaxes the assumption ofm=nfor the classical bounds of two statistics MMDband MMD2uand derives the general bounds based onmn.The yielded results show that the classical bounds derived in [1] are the special cases of our general bounds.The random sample partition (RSP)[5]is a new big data representation model.In future,we will use the MMD statistics with general bounds to determine RSP for big data management and analysis.In addition,we will evaluate the complexity of RSP data block based on these general bounds.