Similar Early Growth of Out-of-time-ordered Correlators in Quantum Chaotic and Integrable Ising Chains?

Hua Yan (顏華), Jiao-Zi Wang (王驕子), and Wen-Ge Wang (王文閣)

Department of Modern Physics, University of Science and Technology of China, Hefei 230026, China

Abstract Previous studies show that, in quantum chaotic and integrable systems, the so-called out-of-time-ordered correlator (OTOC) generically behaves differently at long times, while, it may show similar early growth in one-body systems.In this paper, by means of numerical simulations, it is shown that OTOC has similar early growth in two quantum many-body systems, one integrable and one chaotic.

Key words:quantum chaotic system, quantum integrable system, out-of-time-ordered correlator

1 Introduction

In recent years, the so-called out-of-time-ordered correlator(OTOC)has attracted a lot of attention in several fields of physics, particularly high-energy physics, condensed matter physics, and quantum information.[1?15]Experimentally, it has been studied via nuclear magnetic resonance[16]and ion traps.[17]Study of this quantity can be traced back to an earlier work by Larkin and Ovchinnikov in 1969[1]in the context of superconductivity, as a measure for the instability of semi-classical trajectories of electrons scattered by impurities in a superconductor; its growth rate was found given by the classical Lyapunov exponentλL.Recently, it was proposed that OTOC may be used as a measure for quantum chaos in interacting quantum many-body systems.[18]

Quantitatively, denoted byC(l,t), OTOC is written as

whereWl(t)=eiHtWle?iHtindicates the Heisenberg evolution of an operatorWlandTr(e?βHO)/Tr(e?βH) indicates the initial thermal average at a temperature with 1/β=kBT.Here,Wlrepresents a local operator at a sitelandV0is an operator at another site (usually fixed).

In the specific case thatWlandV0are Hermitian and unitary (e.g., when they are Pauli operators), it was found thatC(l,t)=1?ReF(l,t), whereF(l,t)≡and grows exponentially at early times

whereλcis a parameter andvBis the so-called butterfly velocity.[5,11]Under nature assumptions, it was found thatλcis bounded by 2π/βin quantum systems.[2?4,6]Moreover, for local interactions in spatially extended lattice models, Eq.(2) is not valid for long times andC(l,t)is bounded according to the Lieb-Robinson theorem,[7,19]

wherevLRis certain parameter.

One should note that,althoughλcis usually called the Lyapunov exponent,it is not necessarily the one that characterizes the sensitivity of chaotic motion in classical systems, namely, the parameterλLdiscussed above.In fact,in the kicked rotor model[20?21]and in the Dicke model,[22]OTOC was found to grow asC(t)～Furthermore, early growth of OTOC was found to show similar behaviors in some integrable and chaotic one-body systems (billiards).[23?25]While, it is unclear whether OTOC may show this type of similar behavior in manybody systems.

It is known that, for systems such as an integrable quantum Ising chain,[12]a Luttinger liquid,[26]and some models exhibiting many-body localization,[27?28]OTOC shows early power-law growths.But, a comparison of these early behaviors and those in quantum chaotic systems has not been done.In this paper, we carry out this study and compare the early growth of OTOC in two Ising chains as quantum many-body systems, one being integrable and the other chaotic.These two chains have similar overall properties such as energy size and averaged density of states.This feature makes it sensible to give a quantitative comparison for the OTOC’s early growths.Our numerical simulations show that the two growths are very close, implying that the parameterλchas nothing to do with whether the system is integrable or chaotic.

2 Models Employed

We study OTOC in two models of spin chain.One is the well-known quantum Ising chain in transverse field,which is integrable, with the following Hamiltonian,

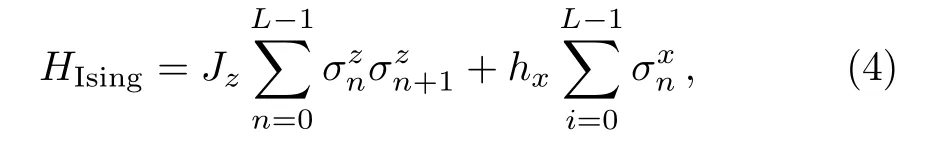
and the other is a defect Ising chain,

withk≠ 0,L.We study under both the periodic boundary condition withσz0=σzLand the open boundary condition.In both Ising chains,Jz=hx=1.In the defect Ising chain, the parametersd1anddkare adjusted, such that the chain is a quantum chaotic system, that is, the nearest-level-spacing distributionP(s)is close to the Wigner-Dyson distributionPW(s)=(π/2)sexp(?(π/4)s2).Specifically,d1=0.5,dk=1.0,k=6, andL=11 (see Fig.1).

Recently, based on semiclassical analysis it was found that certain statistical property of eigenfunctions can also be employed as a measure for quantum chaos,and this is also useful in systems without any classical counterpart.[29?30]Let us consider eigenstatesof the defect Ising chain,Hdefect=Eα, and their expansions in the spin configuration basis, i.e.,Cαi=.The difference between the distribution of the following rescaled components of eigenfunctions,

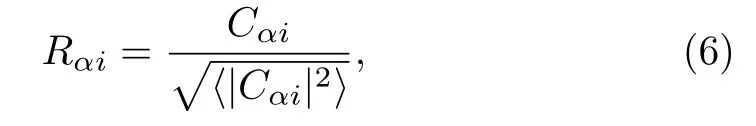
and the Gaussian distribution can be regarded as a measure to quantum chaos.Here,indicates the average shape of the eigenfunctions.As seen in Fig.1,this measure gives results in consistency with those given by the spectral measure discussed above.

Fig.1 (Color online) (a) The nearest-level-spacing distribution P(s) (histogram) of the defect Ising chain under the periodic boundary condition.The dashed line (red) indicates the Wigner-Dyson distribution and the dashed-dotted line (blue) represents the Poisson distribution.(b) Similar to (a), but under the open boundary condition.(c) The distribution of rescaled components Rαi of eigenfunctions in the middle energy region (squares).The dashed line (red)indicates the Gaussian distribution.Parameters: d1=0.5, dk=1.0, k=6, and L=11 (the same for the following figures).

3 Numerical Simulations for OTOC

Below, we first discuss early growth of OTOC in the quantum chaotic system, namely in the defect Ising chain with parameters given above.Then, we compare growths of OTOC obtained in chaotic and integrable Ising chains.

In the computation of OTOC, the operatorsWlandV0are taken as Pauli matrices at thel-th site and at the first site, respectively,

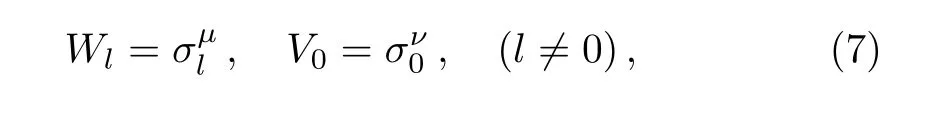
whereμ,ν=x,y,zindicate directions for the Pauli operators.For these operatorsWlandV0, the OTOC has a relatively simple expression,

where

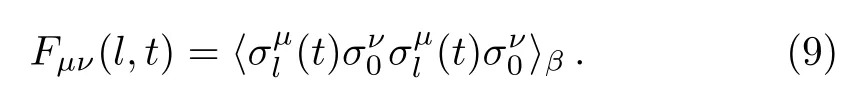
Below, we focus on the two cases of (μ,ν)=(x,x) and(z,z).As discussed in Ref.[12], OTOC behaves differently in these two cases in the integrable Ising chain.

It is useful to give a brief discussion for behaviors of OTOC.Sincel≠ 0, initially,Wl(0) is commutable withV0and, hence,Cμν(l,0)=0.To get an idea about OTOC’s time evolution,let us consider a Baker-Campbell-Huasdorff expansion ofWl(t),[7]which gives

For extremely short timest,Wl(t).With the increase of time, higher-order terms on the right-hand side(rhs)of Eq.(10)should be taken into account in the computation of OTOC.In the two spin chains discussed above,each site is coupled to its neighboring sites only.Hence,for sufficiently short timet,Wl(t) is approximately commutable withV0and, hence,Cμν(l,0)0.

With further increase of the timet, beyond some time scale denoted bytB, thel-th term (it)l[H,...,[H,Wl]]/l!on the rhs of Eq.(10) becomes nonnegligible and, thus,the OTOC gets nonnegligible values.Clearly, the value oftBshould increase withlunder the open boundary condition.These features can be seen in Fig.2, where the early evolution of ReFμν(l,t)=1?Cμν(l,t) is plotted.When Eq.(2) is valid,tBmay be defined by the relationtB=l/vB.Then, one can compute the butterfly velocity, which givesvB ?2.0 as shown in the inset of Fig.2, in agreement with the theoretical prediction given byvB=2Jz/hx=2.[12]

Fig.2 (Color online)Variation of ReFzz(l,t)=1?Czz(l,t)with the time t in the defect Ising chain under the open boundary condition.Inset:Change of a time scale tB with the site number l.

Numerical simulations for the dependence of the time evolution of the OTOC on the initial condition,namely,on the temperatureβ, is shown in Fig.3 for the defect Ising chain under the open boundary condition.It is seen that the early growth of OTOC is almost independent of the value ofβ.In other words, the early growth is insensitive to the initial energy for initial states lying in the middle energy region of the model.We found that a common feature of the eigenfunctions in this region of the model is that they spread over almost all the spin configuration basis states.[29?31]Perhaps, this wide-spreading feature plays an important role in the early growth of OTOC.For long times, OTOC behaves differently depending on the value ofβ; it drops faster for larger value ofβ.

Fig.3 (Color online) Variation of Cxx(l,t) with the time t at different initial temperature β, in the defect quantum Ising chain with l=5 and under the open boundary condition.The early increase of the OTOC is almost independent of the value of β.

Fig.4 (Color online) Comparison of early growths of OTOC in integrable and nonintegrable (chaotic) systems,for (Wl,V0)=(σzl,σz0) and (σxl,σx0) with l=5.(a):open boundary condition, and (b):periodic boundary condition.

Under the periodic boundary condition, the early growth of OTOC was also studied.The obtained results are basically similar to those given in the above two figures, particularly, with similar Butterfly velocityvBbut with different values of the growth-starting timetB.

Finally, we discuss a main observation of this paper.That is,in the two spin chains as quantum many-body systems, our numerical simulations show that OTOC shows similar early growth in integrable and chaotic systems.We have studied OTOC for two pairs of local operators,i.e., (Wl,V0)=(σzl,σz0) and (σxl,σx0), under both the periodic and open boundary conditions (Fig.4).Under the periodic boundary condition, in the early-growth region,the values ofCμμ(l,t) (μ=x,z) in the integrable Ising model are very close to the corresponding values in the nonintegrable (chaotic) defect Ising model.For the open boundary condition, the values are also close, though not as close as in the above case.

The above-discussed closeness of early growth of OTOC in integrable and chaotic systems shows that early growth of OTOC can not be employed as a measure for quantum chaos.For relatively long times, the numerical results in Fig.4 show certain difference between integrable and chaotic systems, except for the squares in the lower panel which are close to the values of chaotic systems.To show the difference more clearly,one needs to compute for even longer times, at which OTOC has power-law decay in the integrable Ising chain.[12](See Ref.[32]for a recent study,which shows qualitative difference between OTOC’s long-time behaviors in integrable and chaotic systems.)

4 Concluding Remarks

It is found by numerical simulations that the OTOC in two quantum many-body systems, one integrable and the other chaotic, show very close early growth under the periodic boundary condition, and close early growth under the open boundary condition.The early growth is important in quantum chaotic systems, because the OTOC approaches its saturation value after this early growth.

Theoretical understanding of the above observation is still lacking.One clue for future investigation is given by the following property of classical systems, that is, the early motion of an integrable system, which has many degrees of freedom with incommensurable frequencies, may exhibit quite irregular features.In fact, it is this behavior of integrable systems that leads to the so-called Fermigolden-rule decay of quantum Loschmidt echo in integrable systems, which was first found in quantum chaotic systems.[33]

A note.After this work was finished, the authors got to know that a similar behavior of the early growth of OTOC was reported in Ref.[32],where a different chaotic Ising chain had been studied.