Unifying quantum heat transfer and superradiant signature in a nonequilibrium collective-qubit system:A polaron-transformed Redf ield approach*

Xu-M in Chen(陳許敏) and ChenWang(王晨)

1DepartmentofPhysics,Hangzhou DianziUniversity,Hangzhou 310018,China

2DepartmentofPhysics,Zhejiang NormalUniversity,Jinhua321004,China

(Received 27December2018;revisedmanuscript received 7 February 2019;published online4 April2019)

Keywords:quantum transport,heat conduction,phonons or vibrational states in low-dimensional structures

1.Introduction

Understanding themechanism of nonequilibrium quantum transport in low dimensional systems is a long-standing challenge,which has been extensively investigated from solid-state physics,[1]quantum thermodynamics,[2]molecular electronics[3]to quantum biology.[4]In particular,quantum thermal transport,where the particle and heat f lows are modulated by the temperature bias,has triggered the emergence of phonics.[5–7]Phonons have been successfully utilized to fabricate various functional devices,such as thermal diode,memory,and transistor.[8–11]In analogy to phonics,quantum heat transfermediated by the spin(e.g.,anharmonic molecule or qubit)has also been intensively analyzed in a sim ilar way,which leads to the realization of quantum spinthermal transistor,[12,13]spin heatengine,[14–16]and nonequilibrium spin network.[17,18]

As a genericmodel to describe quantum heat transfer at the nanoscale,the nonequilibrium spin-bosonmodel(NESB)is composed of a two-level-system(TLS)that is coupled to two thermalbaths,[19]whichwasoriginally proposed to study the quantum dissipation.[20–22]Many approaches have been explored to investigate the underlying mechanism of heat transfer in the NESB.[23–34]Analytically,the Redf ield scheme is properly introduced to investigate the sequential process in theweak spin–bath interaction regime,where two thermal baths show additive contributions to the heat transfer.[14,35]However,the Redf ield approach breaks down in the strong spin–bath interaction regime,where themultiphonon excitations should be involved to characterize the nonequilibrium heat-exchange.Then,the nonequilibrium noninteracting blip approximation(NIBA)can be applied to study baths induced nonadditive and cooperative transfer processes.[23,36–39]However,bothmethodsare found tohave theirown limitations;i.e.,the Redf ield approach is unable to capture themulti-phonon processes in the strong coupling regime,and the heat current based on thenonequilibrium NIBA schemedoesnotshow linear proportion to the coupling strength in the weak coupling regime.[38]Recently,the nonequilibrium polaron-transformed Redf ield equation(NE-PTRE)was proposed to successfully unify the steady stateheatcurrent in the NESB.[32,40,41]However,an exploration of the NE-PTRE to studymore nonequilibrium spin systems is lacking butisurgently required for the spin-based quantum heat transfer.This paper aims to f ill this gap by applying the NE-PTRE to analyze the heat transfer in the collective-qubitmodel.

Recently,a superradiantsignatureof quantum heat transfer has been discovered in the collective-qubit system with weak qubit–bath interaction.[42,43]The steady state superradiance describes the effect that qubits collectively exchange energy with thermal baths,resulting in the current scaling as J～N2s,with Nsthe number of qubits.In sharp contrast,the superradiantheat transfer vanishes in the strong coupling regime based on the nonequilibrium NIBA under the Marcusapproximation.[44]Hence,the steady state behavior of the collective-qubit system is signif icant distinct from each other in lim iting interaction regimes.It is consequently demanding to analyze the heat transfer feature from weak to strong couplings from aunif ied perspective.

To address these problems,we extend the NE-PTRE combined with full counting statistics(FCS)[45,46]to investigate quantum heat transfer in the collective-qubit system.The counting-f ield dependent NE-PTRE successfully unif ies the currentand f luctuations(e.g.,heat current,currentnoise,skewness),with the incoherent picture in the weak quit–bath coupling lim itand themulti-phonon excited transfer picture in thestrong coupling lim it.Moreover,superradiantheattransfer is investigated at large temperaturebias,[42]and thedisappearance of the superradiant signature is explained by enlarging thenumberofqubitsbeyond theweak qubit–bath interaction.

This paper is organized as follows.In Section 2,the collective-qubitmodel and the NE-PTRE are described.In Section 3,FCS isbrief ly introduced and the counting-f ield dependentNE-PTRE isderived,which enablesus to analyze the steady stateheattransfer.In Section4,theheatcurrent,current noise,and skewness are all found to hold the unif ied features by extending theapplication of theNE-PTRE.In Section 5,we study the transition of superradiantheat transfer from weak to strong couplings,and explain the vanishingmechanism of superradiantsignaturewith large number of qubits.In the f inal section,we presenta concise summary.

2.Nonequilibrium collective-qubit system

2.1.M odel

The nonequilibrium energy transfer in the collectivequbitsystem,which interactswith two thermalbaths,ismodeled as?H=?Hs+∑u=L,R(?Hub+?Vu).Thecollective-qubitmodel isdescribed as where the collective angular-momentum operators are?Ja=(a=x,y,z)withbeing the Paulioperator of the i-th qubit,Nsis thenumberofqubits,εandΔare the Zeeman splitting energy and the coherent tunneling strength of the angularmomentum operator,respectively.In the lim itof Ns=1,the Ham iltonian in Eq.(1)is reduced to the sem inalnonequilibrium spin-bosonmodel.[19,35]The u-th thermalbath iscomposed ofnoninteracting bosons,shown aswherecreates(annihilates)one phonon with frequencyωk.The system–bath interaction isgiven by

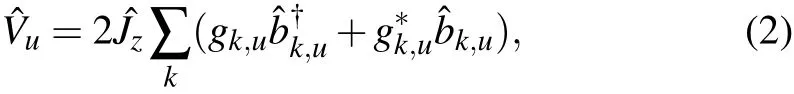
where gk,uis the coupling strength between the angularmomentum and the u-th thermal bath,and is characterized by the spectral function Gu(ω)=4π∑k|gk,u|2δ(ω-ωk).In this paper,we select the spectral function having the super-Ohm ic form Gu(ω)=παuω3/ω2cexp(-ω/ωc),whereαuis the coupling strength andωcis the cutoff frequency of the thermal baths.The super-Ohm ic spectrum has been extensively considered to investigate the quantum dissipative dynam ics and transport in molecular electronics,[47–49]solidstate devices,[50]and light-harvesting complexes.[51,52]

To analyze the multi-phonon involved energy transfer processes,we apply the canonical transformation?U=exp[i?Jz∑u?Bu]to the Ham iltonian?H as?H′=?U??H?U=?H′s+[53,54]where the collective phononmomentum is?Bu=2i.A fter the transformation,

themodif ied system Ham iltonian isgiven by where the factorη=〈cos?B〉isspecif ied as

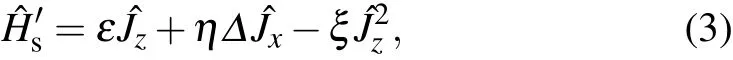
2.2.Nonequilibrium polaron-transformed Red f ield equation

Weapply theNE-PTRE to investigate thedynam icsof the collective-qubitmodel.The NE-PTRE,which is one type of thequantum masterequation,hasbeen successfully applied to unify the nonequilibrium energy transfer in the sem inal spinbosonmodel.[32,41]It isknown that themodif ied system–bath interaction disappears under the thermal average(〈?V′u〉=0).Hence,itmay be safe to perturb〈?V′u〉up to the second order to obtain the quantum master equation.Under the Born approximation,the density operator of thewhole system can be decomposed as?ρ(t)=?ρs(t)??ρb,where?ρs(t)is thedensity operatorof the qubitsand?ρb=e-∑u?Hub/kBTu/Trb{e-∑u?Hub/kBTu}is the density operatorof the bathsatequilibrium.The quantum masterequation in theMarkovian lim it isobtained as

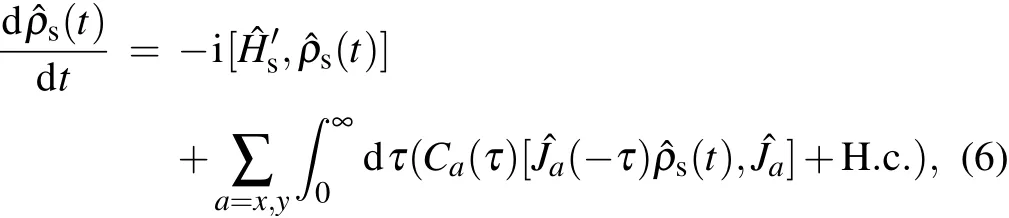
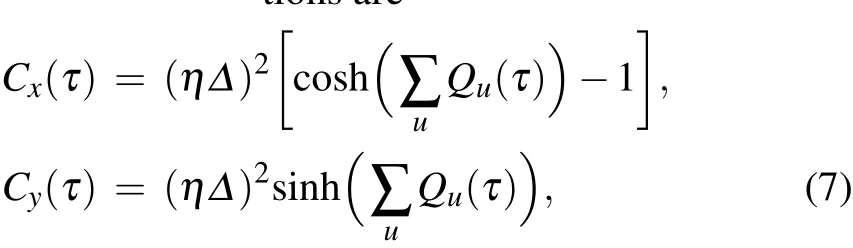
where the correlation functionsare with the phonon propagator in u-th thermal bath Qu(τ)=4∑k|gk,u/ωk|2[cosωkτ(2nk,u+1)-isinωkτ].Furthermore,in the eigen-basis?H′s|φn〉=En|φn〉,the dynam ical equation can be re-expressed as

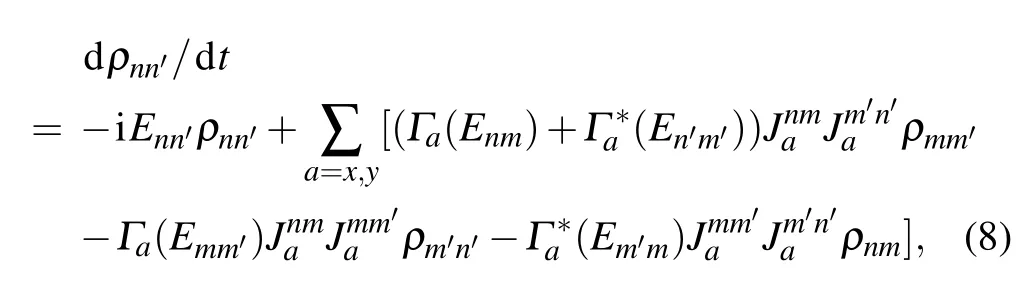
where the transition rate isΓa(ω)=∫∞0dτCa(τ)e-iωτand the element isρnn′=〈φn|?ρs(t)|φn′〉.The rateΓx(y)(Enm)describes that even(odd)number phonons are involved in the transfer processbetween thestates|φn〉and|φm〉.

In the weak qubit–bath coupling lim it,the heat transfer is dom inated by the sequential process andη≈1.Thus,the correlation function Cy(τ)is reduced to Cy(τ)≈Δ2[∑uQu(τ)],and Cx(τ)≈0 by ignoring the high-order correlations. Accordingly,the lowest order of the transition rateΓ(1)y(ω)includes the termΔ2(QL(ω)+QR(ω)),with Qv(ω)=∫dτe-iωτQv(τ).Moreover,allof the off-diagonal elements of the qubits density matrix approach zero at the steady state(not shown here,which is quite sim ilar to the resultin Fig.1).Considering thecommutating relation[?H′s,?Jz]=-iΔ?Jy,thequantum masterequation in Eq.(8)after long time evolution issimplif ied as

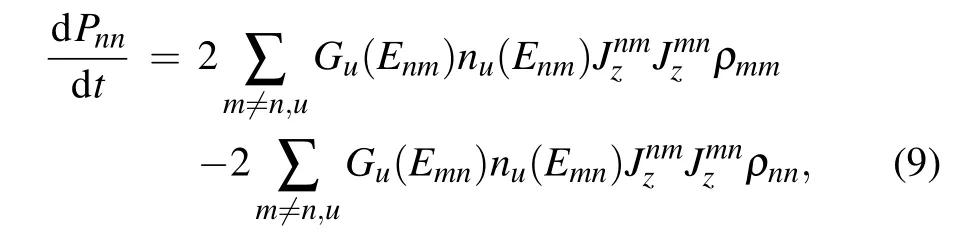
which isidentical to thedynamicalequation based on theRedf ield scheme(see Appendix A for the details).

In the strong qubit–bath interaction lim it,the coherent tunneling ofqubits in Eq.(3)isdramatically suppressed(η≈0),and thecorrelation factorη2e-∑uQu(τ)vanishes.However,the other factorη2e∑uQu(τ)is kept f inite,which contributes to the quantum heat transfer.Hence,the correlation functions in Eq.(7)are reduced to Cx(τ)=Cy(τ)=(ηΔ)2[exp∑uQu(τ)].Consequently,themasterequation in Eq.(8)on the localbasis{|φn〉}with(ε?Jz-ξ?J2z)|φn〉=(εn-ξn2)|φn〉is changed to

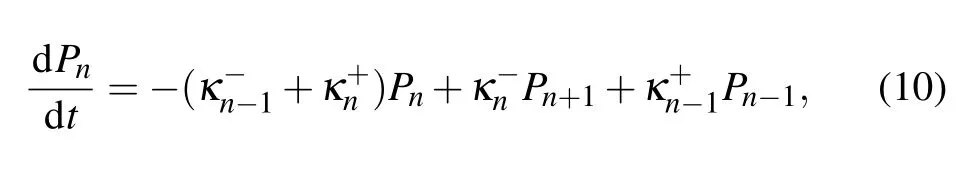
3.Fullcounting statisticsof heat current

3.1.Thegeneral theory

Full counting statistics is a two-time projection protocol tomeasure the current and f luctuations.[45,46]For the energy transfer in themulti-terminal setup,thegenerating function is generally given by[55]

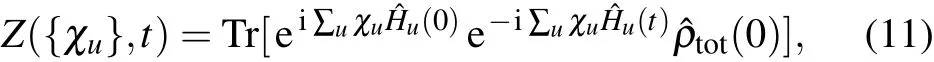
whereχuis the counting-f ield parameter to count the energy f low into the u-th bath with the Ham iltonian ?Hu, ?Hu(t)= ?U??Hu?U with the propagator ?U=e-i?Ht,and ?ρtot(0)is the initial density matrix of the whole system. Moreover,considering the modif ied propagator ?U{χu}(t)= ei∑uχu?Hu/2?U(t)e-i∑uχu?Hu/2,it can be reexpressed as ?U{χu}(t)=exp(-i?H{χu}t),with ?H{χu}=ei∑uχu?Hu/2?H e-i∑uχu?Hu/2.Hence,the generating function is re-expressed as

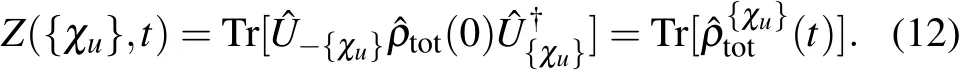
After the long-time evolution,the cumulantgenerating function isobtained as

Therefore,the n-th cumulantof heat current f luctuations into the u-th bath isgiven by Specif ically,the lowest cumulant is the steady state heat current

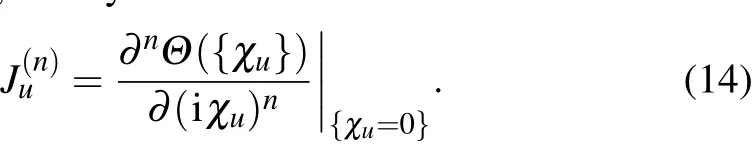
3.2.Counting-f ield dependent NE-PTRE

To count the heat f low into the right-hand thermal bath,we introduce the counting f ield parameters as?Hχ=ei?HRbχ/2?H e-i?HRbχ/2,[55]which results in

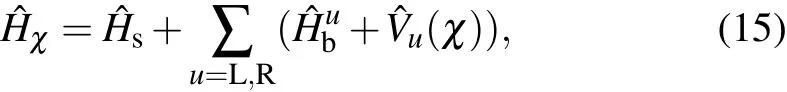
where the system–bath interactionwith the counting f ield parameter isexpressed as

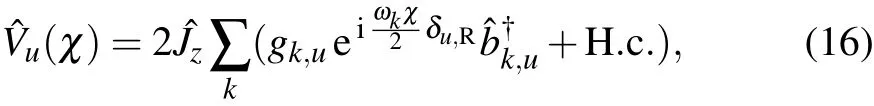
withδR,R=1 andδL,R=0.Then,after the canonical transformation?H′χ=U?χ?HχUχwith transformation operator U=exp[i?Jz∑u?Bu(χ)]and themodif ied Hamiltonian isgiven by

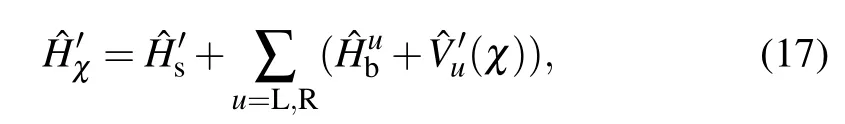
where the modif ied system–bath interaction with counting f ield parameter isgiven by

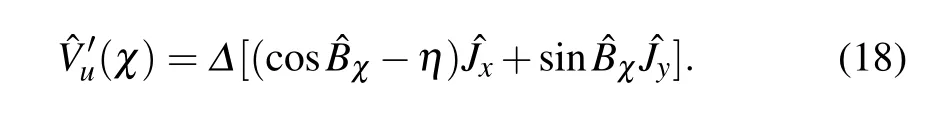
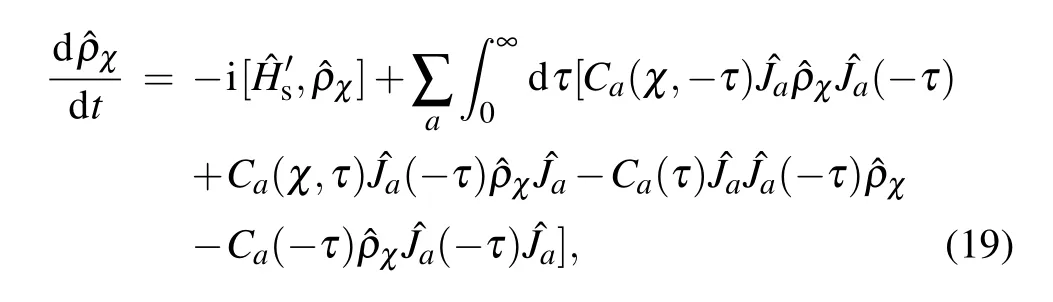
By perturbing?V′u(χ)under the Born–Markov approximation,weobtain the second-orderquantum masterequation as where the correlation functionswith counting f ield parameter are In absence of the counting f ield parameter,the correlation functions are reduced to the standard version in Eq.(7).In the eigen-basis,the dynam ics of the density matrix elements can be specif ied as where the transition ratesare

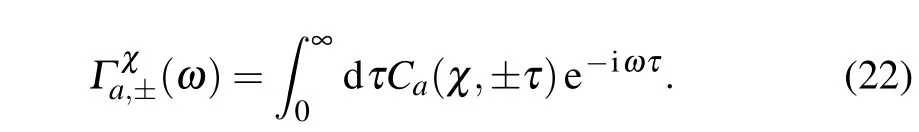
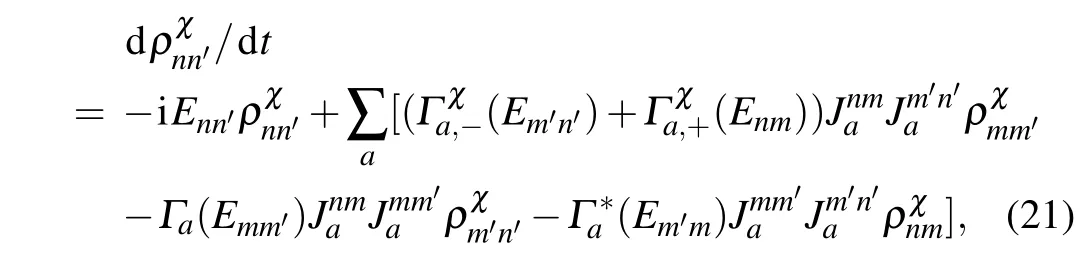
Ifwe reorganize the reduced densitymatrix of collectivequbit from thematrix form to the vector expression,the dynam icalequation in Eq.(21)isexpressed as where??(χ)is thesuperoperator to dom inate thesystem evolution.Then,the cumulantgenerating function at t-time isgiven by

where|ρ(0)〉is the vector form of the initial system density matrix,and〈I|is the left-eigenvector of??as〈I|??=0,with the normalization relation〈I|ρχ=0(t)〉=1.Hence,heat current f luctuations at the steady state can be straightforwardly obtained by follow ing Eq.(14).4.Unif ied steady stateheat current

Quantum heat transfer in the NESB has been successfully investigated based on the Redf ield and noninteractingblip approximation schemesin theweak and strongqubit–bath coupling lim its,respectively.However,the steady state heat currentwas found to be distinct from each other in a broad coupling regime.[38]Recently,the nonequilibrium polarontransformed Redf ield equation combined with full counting statisticswasproposed to unify theheatcurrentbetween these two lim iting approaches.[32,41]

Here,we try to extend the counting-f ield dependent NE-PTRE to unify the heat transfer in the nonequilibrium collective-qubitmodel in Fig.1.At resonance(ε=0),we f irst analyze the steady state heat current in Figs.1(a)and 1(d).It clearly exhibits the turnover behavior,which unif ies the counterpartswithin theRedf ield and NIBAmethodsas the qubit–bath coupling strength approaches theweak and strong coupling lim its.Although we admit that to gain an analytical expression of theheatcurrentatarbitrary qubit–bath coupling is ratherdiff icult,itcan beobtained in lim iting regimes.Here,westudy theanalyticalexpression of thesteady stateheatcurrentwith Ns=2.Specif ically,in the weak interaction lim it,the heat current is analytically expressed as(see Eq.(A9)in Appendix A)

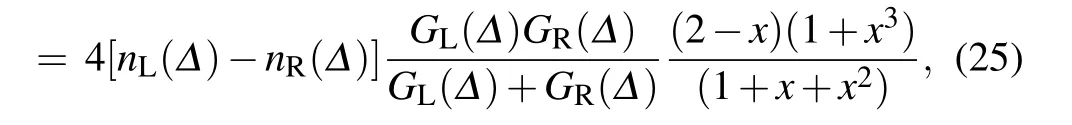
J weak where the coeff icient

which is linearly proportional to the qubit–bath coupling strength.The current in Eq.(25)is the special case of the general expression in Eq.(A9).It is found in Fig.1(a)that Jweakbecomes identical to the counterpart from NE-PTRE in theweak coupling lim it(e.g.,α=0.001).Moreover,itshould be noted that the current Jweakin Eq.(25)with Ns=2 has a sim ilar expression to the case in the standard NESB(Ns=1)in theweak coupling lim it,which are both proportional to the thermodynam ic bias(i.e.,J∝[nL(Δ)-nR(Δ)]).[23]

While in the strong coupling limit,the dynamical equation in Eq.(19)with thenumberof qubits Ns=2 is reduced to the kinetic form(see Eq.(B4)in Appendix B)

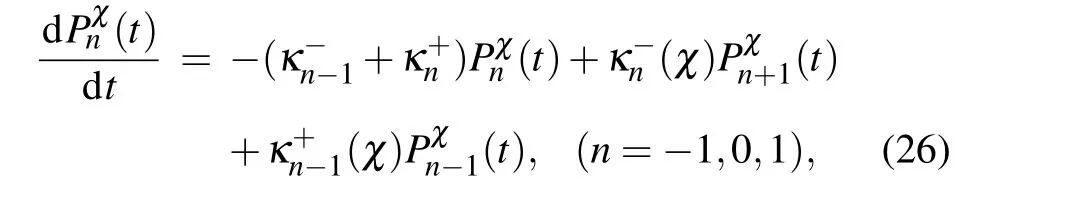
where the population is Pχn=〈1,n|?ρχ(t)|1,n〉with?Jz|1,n〉=n|1,n〉.The transition rate is

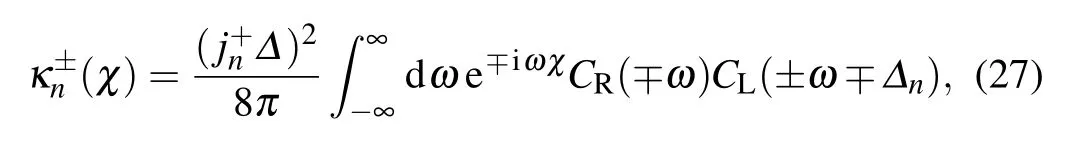
Fig.1.Comparisons of steady state current f luctuations based on the NE-PTRE with counterpartswithin the Redf ield and NIBA schemes:(a)–(c)at resonance(ε=0)and(d)–(f)atoff-resonance(ε=1),by tuning qubit–bath coupling strengthα.Theother parametersare N s=2,Δ=1,ωc=6,T L=1.5,and T R=0.5.

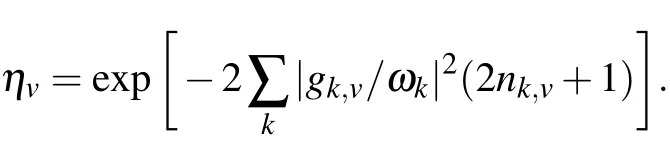
-1/2=1),then the rateκ±n(χ)is reduced to the standard NESB result(see Eq.(20)in Ref.[36]).Thus,the cumulantgenerating function atsteady state isgiven by

whereκ±-1(χ)=κ?0(χ).Consequently,the heat current is given by

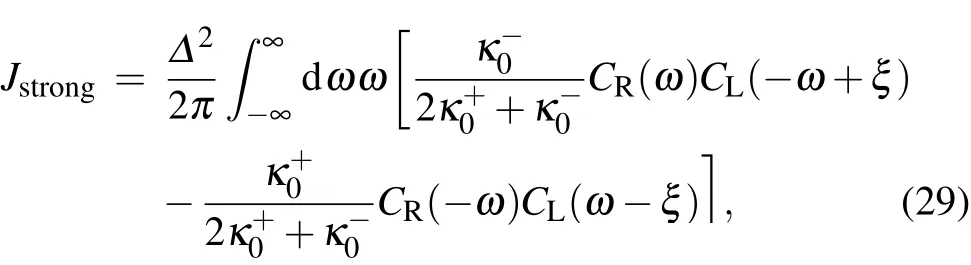
where the f irst(second)term describes the process thatas the qubits release(gain)energyξ,the right-hand bath absorbs(emits)phonon energyωand the left-hand bath obtains(provides)the remaining energyξ-ω.Jstrongshows a similar structurewith the counterpart in the standard NESB,which is jointly contributed by the two thermalbaths.[36]Moreover,the expression of Jstrongcaptures the turnover feature of heat current in Figs.1(a)and 1(d)as shown by the dashed-blue lines with squares.Hence,we conclude that the steady state heat f lux is clearly unif ied in the nonequilibrium collective-qubit model.

Next,we analyze the zero-frequency current noise and skewness in Figs.1(b),1(c),1(e),and 1(f).It is interesting to f ind that the results based on the NE-PTRE also perfectly bridge the limiting counterparts in theweak and strong coupling regimes,which may demonstrate the unif ication of current f luctuations in the extended spin-boson systems(e.g.,collective-qubit model). Moreover,the turnover behavior which is presented in the current is unraveled for the second and the third cumulants.A lthough notshown here,higher cumulantsof current f luctuationsalso show suchunif ied features.We should note that all above results are valid both at resonant and off-resonant conditions,which clearly exhibits that full counting statisticsof the heat current isgenerally unif ied within the NE-PTRE scheme.

5.Suppression of superradiantheat transfer

The superradiant effect,which describes that the system exhibits collective response under themodulation of the external f ield or thermalbath,hasbeen extensively investigated in quantum phase transition,[56,57]criticalheatengine,[58]and quantum transport.[42,43]In particular,quantum heat transfer in the nonequilibrium large-spin system shows the superradiant signature in the weak spin–bath coupling regime.[42]Specif ically,undera large temperaturebias(e.g.,TL?TR),the steady stateheatcurrent isexpressed as

which follows the condition x/(1-x)?Ns.Itshould benoted thatequation(30)isa special case of the current in Eq.(A9)in Appendix A.However,with thestrong spin–bath interaction based on theNIBA schemecombinedwith theMarcusapproximation,itis found thatsuch superradianttransfervanishes.[44]Hence,we apply the NE-PTRE to clarify this apparent paradox.

We f irst study the effect of the temperature biasΔT on the heat current in Fig.2(a)with spin-bath coupling strength α=0.01?{Δ,ωc},which is considered weak for the seminal spin-boson model(η≈1).It is found that the current shows monotonic enhancement by increasing bothΔT and Ns.Moreover,at large temperature bias(e.g.,TL=8 and TR=0.4),thecurrentbecomesnearly stablewith largenumber ofqubits,which isclearly exhibited in Fig.2(b)(e.g.,Ns=32).While for relatively small number of qubits(e.g.,Ns＜20)in Fig.2(b),the superradiantsignature of heatcurrent isnumerically obtained as J∝Nγswithγ=2.0±0.1(forboth resonance and off-resonance).Thus,it is known that the expression of superradiantheatcurrent in Eq.(30)becomes invalid at large N s.

Fig.2.Behaviors of steady state heat current J by tuning:(a)temperature biasΔT=T L-T R with T R=0.4,ε=0,andα=0.01;(b)the number of qubits N s with T L=8,T R=0.4,andα=0.01;(c)qubit–bath coupling strengthαwith T L=8,T R=0.4,andε=0.The other parametersareΔ=1 andωc=6.

To exploit the origin,we plot the current as a function of the qubit–bath coupling strengthαfor different Nswith TL=8,TR=0.4,andε=0,as shown in Fig.2(c).It is shown that for small Ns(e.g.,Ns=8),the heat f lux exhibits approximately linear increasing behavior in theweak coupling regime(e.g.,α≤0.01).The heat f lux demonstrates the sequential transfer process,where a superradiantheat transfer is accordingly observed,which could be described by the Redf ield scheme.While the current shows distinct behavior for large Nsfrom that for small Nsin the same coupling regime.Forexample,thecurrent for Ns=32with thecoupling strength α=0.01 has already surpassed the turnover pointof the current,while the current for Ns=8 is almost linearly dependent on the coupling strength in the same coupling regime.It is known that the appearance of the turnover point of the current is the signif icant signature of themulti-phonons involved coherent transfer,as exploited in the nonequilibrium spin-bosonmodel.[32]Sinceηisnearly equal to 1 in these two casesand theheatcurrentshowsdifferent features in the same coupling regime,we conclude thatη≈1 doesnotnecessarily correspond to theweak coupling condition.Furthermore,the behavior of the current should be properly described by the NIBA scheme,which resultsin theabsenceofnonequilibrium superradiant signature.Therefore,the effect of superradiant heat transfer in the collective-qubitmodelw illbedramatically suppressed in the large Nsregime;i.e.it is an Ns-dependent phenomenon.

6.Conclusion

In summary,we investigate the quantum heat transfer in the nonequilibrium collective-qubit system by applying the nonequilibrium polaron-transformed Redf ield equation combined with full counting statistics.We f irstanalyze the effect ofqubit–bath coupling on the steady stateheatcurrent,which results in a turnoverbehaviorand issimilar to the counterpart in the nonequilibrium spin-boson model.Interestingly,the currentconsistently bridges the results in theweak and strong coupling lim its,which clearly demonstrates that the heat currentcan beunif ied in themulti-qubitscase.A lthough itshould beadmitted that thegeneralsolution of theheatcurrent isdiff icult to obtain even for Ns=2,the analyticalexpression can be still obtained in the weak and strong couplings based on the Redf ield(Eq.(25))and NIBA(Eq.(29))schemes,respectively.Moreover,the current noise and skewness are shown to be unif ied accordingly.A lthough not shown in the present paper,the unif ication of higher cumulants of heat current can also be observed.Therefore,we propose that full counting statisticsofheatcurrentatsteady state can beunif ied by using the NE-PTRE.

Next,we study the superradiantheat transfer in the high temperature bias regime.It is found thatwith small number of qubits,the heat transfer is described by the sequential process under the Redf ield scheme.The heat current exhibitsan apparent signature of the steady state superradiance.While with the large number of qubits,the superradiant signature of the heat f lux vanishes.The corresponding physical process is described by the NIBA scheme becausemulti-phonons should be involved to contribute to the heat transfer.Therefore,we conclude that the superradiant transfer in the collective-qubitmodel isa size-dependentphenomenon,and itw illbe strongly suppressed by increasing the qubitsnumber.

We believe that based on the counting-f ield dependent NE-PTRE,theunif ied featureofsteady stateheat transfermay be realized in amuch bigger fam ily of the quantum nonequilibrium system,such asaquantum spin-boson network.[18]

Appendix A:Quantum thermal transfer within the Redf ield scheme

The nonequilibrium collective-qubitsystem is expressed as?H=?Hs+∑v=L,R(?Hvb+?Vv),where the qubits Hamiltonian isgiven by the v-th thermal bath is,and the system–bath interaction is

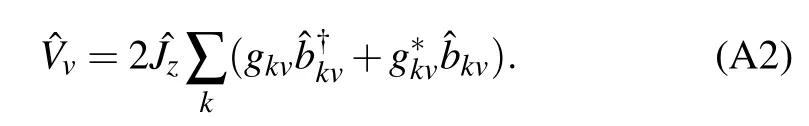
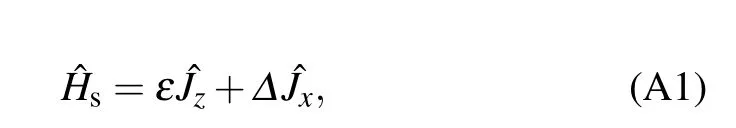
To count the energy f low into the right bath including the full counting statistics,the total Hamiltonian is changed to ?H(χ)=eiχ?HRb/2?H e-iχ?HRb/2=?Hs+∑v(?Hvb+?Vχv),where

Considering theweak qubit–bath interaction,we directly perturb the system–bath interaction in Eq.(A3)up to the second order.Then,based on the Born–Markov approximation,the Redf ield equation isgiven by

d?ρχ(t)d t =-i[?Hs,?ρχ(t)] (A4)-∑v∞0dτTrb{[?Vχv,[?Vχv(-τ),?ρχ(t)??ρb]χ]χ},with the commutating relation[?Aχ,?Bχ]χ=?Aχ?Bχ-?Bχ?A-χ.In the eigen-basis{|φn〉}with?Hs|φn〉=En|φn〉,the dynam ical equation of the system densitymatrix element isgiven by where the counting-f ield dependent density matrix element is,the transition rate is Gv(ω)=,and theBose–Einstein distribution function is nv(ω)=1/[exp(ω/kBTv)-1].

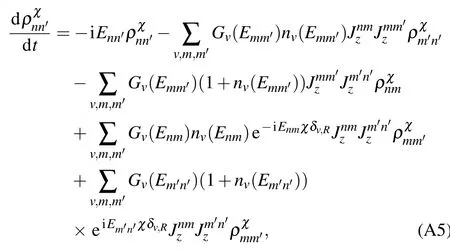
At resonance(ε=0),it is found that the off-diagonalelements of the qubits system in eigen-space vanish at steady state in Figs.A1(a)–A1(c),in theabsenceof the counting f ield(χ=0).Hence,the steady state equation isgiven by

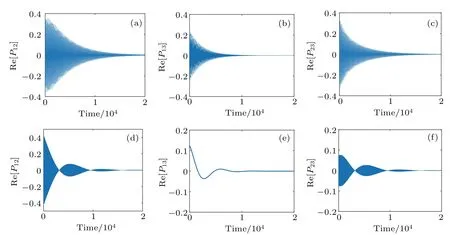
Fig.A1.Dynam icsof theoff-diagonalelementsof the collectivequbits system Pij=〈φi|?ρs(t→∞)|φj〉(a)–(c)at resonance(ε=0)and(d)–(f)atoff-resonance(ε=1),with theeigen-solution?H s|φi〉=Ei|φi〉.The initialstate isgiven by?ρs(0)=|1,-1〉〈1,-1|.Theother parametersare N s=2,Δ=1,α=0.005,ωc=6,T L=1.5,and T R=0.5.

Actually,the system Hamiltonian at resonance is?Hs=Δ?Jx,with the eigen-solution ?Hs|j,m〉x=Δm|j,m〉x(m=-Ns/2,-Ns/2+1,...,Ns/2).Thus,the coeff icient Jnmzcan be specif ied as-m(m±1).Consequently,the steady state population can be analytically obtained as

with the coeff icient

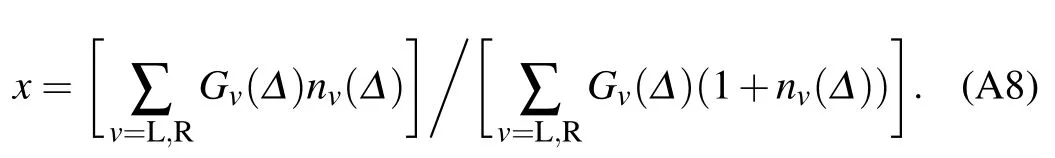
Finally,the steady stateheat f lux isgiven by

where the current factor isexpressed as

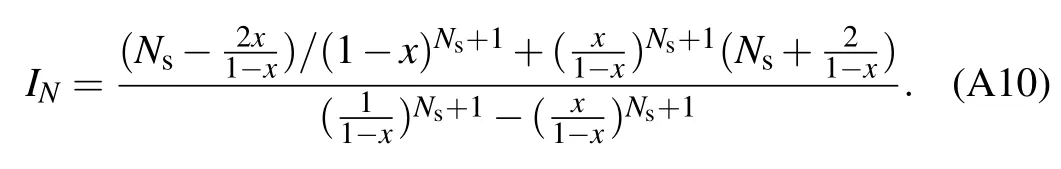
While at the off-resonantcondition(e.g.,ε=1),the offdiagonal elements after long time evolution also vanish,as shown in Figs.A1(d)–A1(f).Hence,the heatcurrent into the right thermalbath isgenerally expressed as

Appendix B:Quantum thermal transfer within the NIBA schemeto obtain themodif ied Hamiltonian of thewholesystem?H′χ=?U?χ?Hχ?Uχas

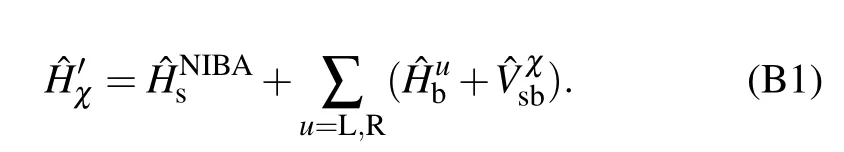
Themodif ied system Hamiltonian isgiven by where the renormalization energy isξ=The eigen-solution isgiven bywith En=εn-ξn2and n=-Ns/2,...,Ns/2.Themodif ied system–bath interaction isgiven by Hence,by perturbing?Vχ

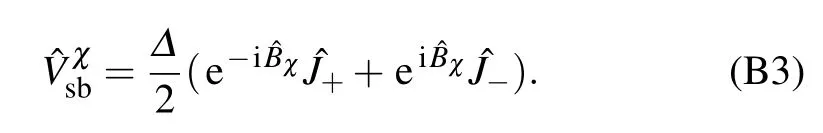
sbup to thesecond order,weobtain the quantum kinetic equation

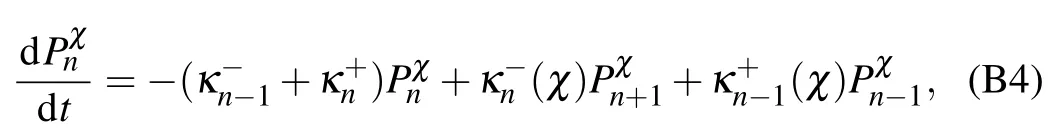
where the counting-f ield dependent population element is Pχn=〈φn|?ρχ(t)|φn〉and themodif ied transition ratesare

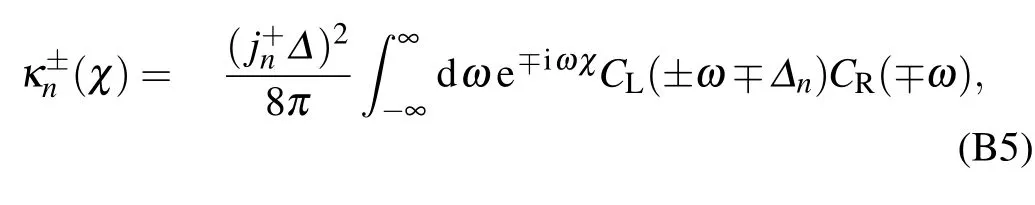
where the coeff icient is j+n=Ns/2(Ns/2+1)-n(n+1),the energy gapΔn=En+1-En=ε-ξ(2n+1),and the correlation function in the frequency domain is with the renormalization factorηv=and the correlation phase In the absence of the counting-f ield parameter(χ=0),this modif ied kinetic equation is identical to the dynam ical equation in Eq.(10).Hence,the heat currentatsteady state isobtained as

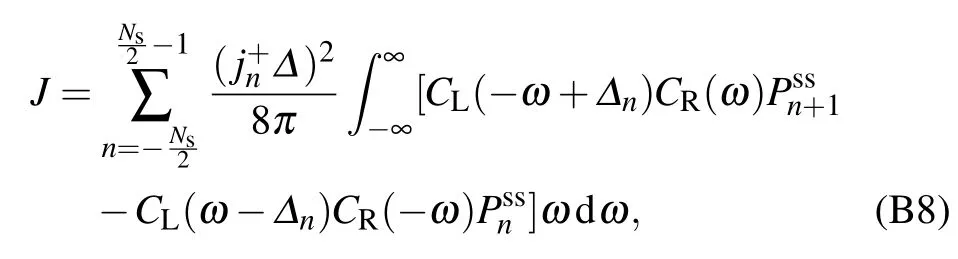
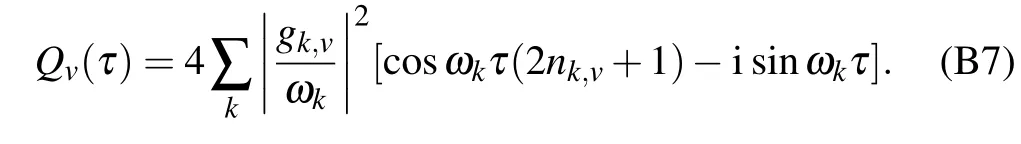
where the steady state population is given by Pnss=〈Ns/2,n|ρ?s(t→∞)|Ns/2,n〉.