一道課本練習題的研究性學習案例一則
北京市北京師范大學出版集團(100875) 岳昌慶
由于篇幅所限,課堂上的實際過程略去,只將主線展示如下:
人民教育出版社義務教育教科書數(shù)學九年級上冊(2014年3月第1版)第83頁練習第2題
例1 如圖1,在⊙O中,AB,AC是互相垂直且相等的兩條弦,OD⊥AB于點D,OE⊥AC于點E,求證:四邊形ADOE是正方形.
分析與略證這是一道練習級別的課本習題,題中涉及一些概念與結(jié)論:AB,AC是交于圓上一點A的兩條互相垂直的弦,且OD,OE分別為其弦心距.由垂徑定理,在同圓或等圓中,等弦對等弦心距.所以OE=OD,故四邊形ADOE是正方形.
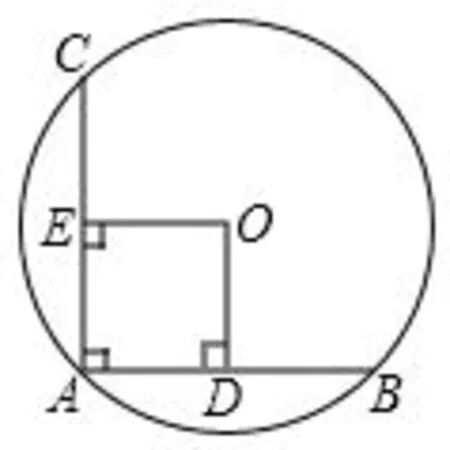
圖1
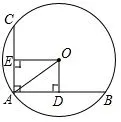
圖2
當我們將“AC=AB”這一條件變?yōu)椴幌嗟葧r,我們看:
例2 (2005年中考四川省卷第12題4分)如圖2,在⊙O中,AB,AC是互相垂直的兩條弦,OD⊥AB于點D,OE⊥AC于點E,且AB=8cm,AC=6 cm,那么⊙O的半徑OA長為___.
分析與略解這時,正方形ADOE變?yōu)榫匦蜛DOE,AD=4,OD=3,所以⊙O的半徑OA長為5 cm.
當我們將垂足A由圓上移至圓內(nèi)時,我們有:
例3 (2011年中考安徽省卷第13題5分)如圖3,⊙O的兩條弦AB,CD互相垂直,垂足為E,且AB=CD,已知CE=1,ED=3,則⊙O的半徑是___.
分析與略解過O作OF⊥CD于點F,過O作OG⊥AB于點F,所以,EF=OG=1,AG=2,故⊙O的半徑為
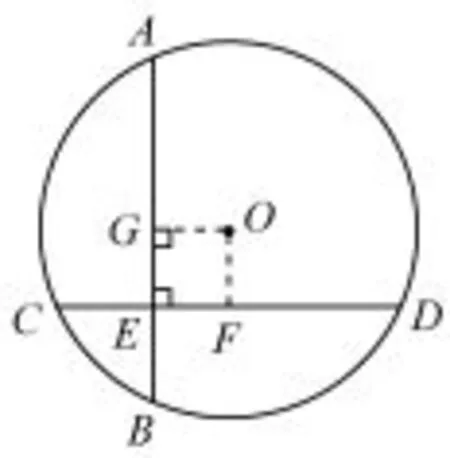
圖3
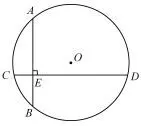
圖4
例4 如圖4,⊙O的兩條弦AB,CD互相垂直,垂足為E,且AB=10,CE=2,ED=10,則⊙O的半徑是____.
分析與略解
當我們將例1中的“AC⊥AB”這一條件變?yōu)樾苯粫r,我們有:
例5 (2011年中考上海市卷第17題4分)如圖5,AB,AC都是⊙O的弦,OM⊥AB,ON⊥AC,垂足分別為M,N,如果MN=3,那么BC=___.
分析與略解由垂徑定理,顯然MN為△ABC的中位線,所以BC=2MN=6.
評注BC的長與AB,AC是否相等沒有關(guān)系,此時四邊形OMAN仍然四點共圓.
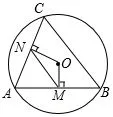
圖5
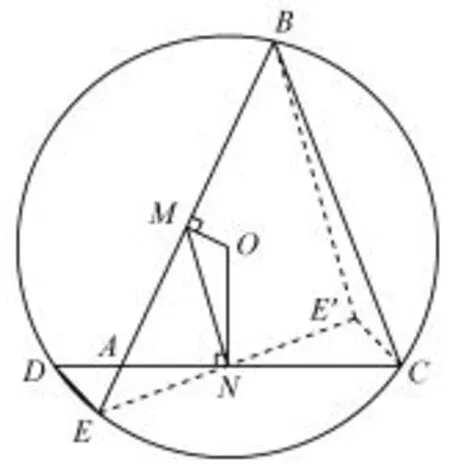
圖6
當我們將例5中的點A由圓上移至圓內(nèi)時,我們有:
例6 如圖6,△ABC的頂點B,C在⊙O上,點A在⊙O內(nèi),CA,BA分別交⊙O于D,E,OM⊥AB于M,ON⊥AC于N,學生課上猜出以下結(jié)論:
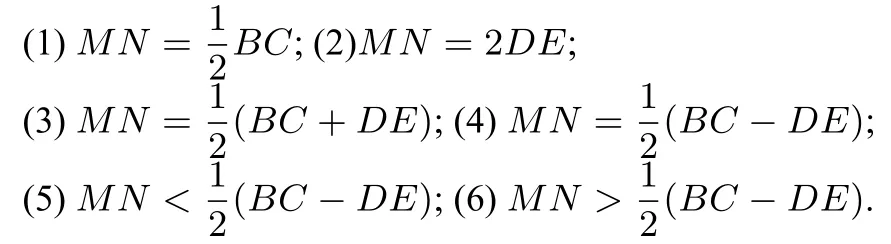
分析與略解由垂徑定理EM=MB,DN=NC,連接EN,延長EN至E′,使EN=NE′,連接CE′,BE′,可得△NDE△NCE′,所以DE=CE′.在△EBE′中,MN為中位線,在△BCE′中,BE′>BC?CE′.所以故(1)~(5)均不成立.實際上,(6)是在學生尋證(1)~(5)的過程中,被動發(fā)現(xiàn)的.
類似不等關(guān)系的中考題,還可順手再舉一例:
例7 (2007年中考四川省成都市A卷第20題9分壓軸題)已知:如圖7,△ABC中,∠ABC=45°,CD⊥AB于D,BF平分 ∠ABC,且BF⊥AC于F,與CD相交于點E,H是邊BC的中點,連結(jié)DH與BF相交于點G.
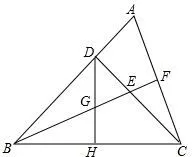
圖7
(1)求證:BE=AC;(2)求證:
(3)CF與BG的大小關(guān)系如何?試證明你的結(jié)論.
分析與略解(1)略;(2)略;(3)CF<BG.
以上探究讓我們看到一道課本練習題,在命題專家的妙手中是怎樣一步步演繹出令人拍案叫絕的中考題,也似是看到了他們各自的心路歷程;同時也給考生提個醒兒:探究題并不總是能找到等量關(guān)系的,不等關(guān)系也是一種關(guān)系.

