兩個正規(guī)p-超可解子群的積

毛月梅馬小箭湯興政

(1.山西大同大學量子信息科學研究所,山西大同 037009)

(2.中國科學技術(shù)大學數(shù)學學院,安徽合肥 230026)

兩個正規(guī)p-超可解子群的積

毛月梅1,2,馬小箭1,湯興政2

(1.山西大同大學量子信息科學研究所,山西大同 037009)

(2.中國科學技術(shù)大學數(shù)學學院,安徽合肥 230026)

本文研究了兩個正規(guī)的p-超可解子群的積構(gòu)成的極小非p-超可解群的結(jié)構(gòu)的問題.利用有限群論和群類論的一些基本方法,獲得了兩個正規(guī)的p-超可解子群的積仍為p-超可解群的一些充分條件,并推廣了文[1]中關(guān)于超可解群的情況.

有限群;超可解群;p-超可解群;Sylow子群

1 引言

有限群論研究中一個基本的事實是兩個正規(guī)可解子群的積是可解群;兩個正規(guī)冪零子群的積是冪零群;但是,兩個正規(guī)超可解(p-超可解)子群的積不一定是超可解群(p-超可解群).自然地,產(chǎn)生了以下兩個問題:

問題1在何種條件下,兩個正規(guī)超可解(p-超可解)子群的積仍然是超可解(p-超可解)的?

問題2(見文獻[2,第II章,問題6.34])能分解為兩個(正規(guī))超可解(p-超可解)子群的積的非超可解群(p-超可解群)有什么樣的結(jié)構(gòu)?

許多群論學者都研究過問題1,比如,文[3–13].特別地,Baer[5]證明了:設G是兩個正規(guī)超可解子群的積,如果G′是冪零的,那么G是超可解的;Friesen[7]證明了:設G是兩個正規(guī)超可解子群M和N的積,如果指數(shù)(|G:M|,|G:N|)=1,那么G是超可解的.最近,郭文彬和Kondrat’ev在文獻[8,11]中研究了能分解為兩個正規(guī)超可解(p-超可解)子群的積的極小非超可解(非p-超可解)群的結(jié)構(gòu),他們證明了:G是兩個正規(guī)超可解(p-超可解)子群的積的極小非超可解群(非p-超可解群)當且僅當G/F(G)是準素數(shù)的極小非交換群.令P1是由所有可以表示成兩個超可解正規(guī)子群積的有限群所構(gòu)成的群類.記P={G|G是非超可解的P1-群,且G的任意P1-真子群和非平凡商群都是超可解的}.文[1]的第五章給出了P-群的結(jié)構(gòu).

作為此類問題的推廣,本文將討論p-超可解群的情況.令(P1)p是由所有可以表示成兩個p-超可解正規(guī)子群積的有限群所構(gòu)成的群類.記Pp={G|G是非p-超可解的(P1)p-群,且G的任意(P1)p-真子群和非平凡商群都是p-超可解的}.本文將分類所有的Pp-群.

本文中用符號G(Gp),U(Up)分別表示所有群(p-群),超可解群(p-超可解群)組成的群類,符號A(p?1)表示所有冪指數(shù)整除p?1的交換群作成的群類.易見,U和A(p?1)都是飽和群系.由文[14,引理2.3]知Up也是一個飽和群系.文中所涉及的群均是有限群.未交待的概念和符號參見文獻[2,15].

2 準備知識

首先介紹兩種p-群,令

注意到Mp(n,1)的極大子群只有〈ap〉=Z(Mp(n,1)),所以Mp(n,1)是一個極小非交換p-群.同樣地,Ep(1,1,1)也是一個極小非交換p-群.文[1]中的定理5.2.6已證明以下四類群是僅有的P-群.

群1設p,q是兩個素數(shù),其中q|p?1且q＞2.P=Fpv1+Fpv2+···+Fpvq是一個域Fp上的q-維向量空間.設ω為Fp上的一個q次本原單位根.令

且令Q=〈α,β,γ〉,這里Q是由元素α,β,γ在矩陣的乘法運算下所生成的一個群,于是Q?Eq(1,1,1).令G=PQ,M=P〈α,β〉且N=P〈α,γ〉,那么M和N是G的兩個正規(guī)的超可解子群且G=MN,但G不是超可解的.將群G記為E(p,q,1).

群2設p,q是兩個素數(shù),其中qn|p?1且n≥2.P=Fpv1+Fpv2+···+Fpvq是一個域Fp上的q-維向量空間.設ω,θ分別為Fp上的一個q,qn次本原單位根.令

且令Q=〈β,γ〉,于是Q?Mq(n,1).令G=PQ,M=P〈β〉和N=P〈βq,γ〉,那么M和N是G的兩個正規(guī)的超可解子群且G=MN,但G不是超可解的.將群G記為M(p,q,n,θ,ω),根據(jù)文[1]中的命題5.2.5,群M(p,q,n,θ,ω)可以簡記為M(p,q,n).

設G=FH,如果H正則地作用在F上.稱G是一個以F為核以H為補的Frobenius群.

群3設p是一個素數(shù)且4|p?1.P=Fpv1+Fpv2是域Fp上的一個2-維向量空間.設θ是Fp上的一個4次本原單位根.令且Q=〈β,γ〉,那么Q?Q8.令G=PQ,M=P〈β〉且N=P〈γ〉,那么M和N均是G的正規(guī)超可解子群且G=MN,但G是一個非超可解的以P為核,以Q為補的Frobenius群,將G記為Q(p,2).

群4設p是一個素數(shù)且4 ?p?1.P=Fpv1+Fpv2是域Fp上的一個2-維向量空間.

令

且Q=〈α,β,γ〉,那么Q?D4.令G=PQ,M=P〈α,β〉且N=P〈α,γ〉,那么M和N均是G的正規(guī)超可解子群且G=MN.但G是一個非超可解群,將G記為D(p,2).

引理2.1(見文獻[1,定理5.2.6])如果群G是一個P-群,那么|π(G)|=2且存在素數(shù)p,q使得G與E(p,q,1),M(p,q,n),Q(p,2)和D(p,2)中的一個同構(gòu).

引理 2.2(見文獻[15,定理1.8.17])假定M是群G的一個正規(guī)冪零子群,如果M∩Φ(G)=1,則M是G的一些極小正規(guī)子群的直積.

引理2.3(見文獻[16,定理2.1.6])假定G是一個p-超可解群且Op′(G)=1,那么p是π(G)中的最大素數(shù),G是超可解的且G有正規(guī)的Sylowp-子群.

下述引理是顯然的.

引理2.4假定N是群G的一個正規(guī)p-子群.如果N≤ZU(G),那么G/CG(N)∈GpA(p?1).

引理2.5(見文獻[17,第1章,定理1.4])設N是群G的一個極小正規(guī)p-子群.如果G/CG(N)∈A(p?1),那么|N|=p.

引理 2.6(見文獻[15,引理1.7.11])假設H/K是群G的一個pd-主因子,則Op(G/CG(H/K))=1.

3 主要結(jié)果

定理3.1假定G是一個Pp-群,則存在素數(shù)q|p?1使得π(G)={p,q}且G與E(p,q,1),M(p,q,n),Q(p,2)和D(p,2)中的某個群同構(gòu).

證因為G是一個Pp-群,所以G是非p-超可解的(P1)p-群且G的任意(P1)p-真子群和任意非平凡商群均是p-超可解的.不妨假設G=MN,其中M,N是G的兩個正規(guī)的p-超可解子群.通過以下步驟實現(xiàn)定理的證明.

(1)Op′(G)=Φ(G)=1且G是p-閉的可解群.

如果上面斷言之一不成立,那么N≠1,其中N=Op′(G)或N=Φ(G).易見,G/N滿足定理的假設.對|G|進行歸納知G/N是p-超可解的.因此G是p-超可解的,矛盾.所以Op′(G)=Φ(G)=1.因為M,N是p-超可解的,所以由引理2.3知p是π(M)和π(N)的最大素數(shù),且M和N均是超可解的.又G=MN,因此p是π(G)中的最大素數(shù)且G是p-閉的可解群.

(2)G有唯一的極小正規(guī)子群K滿足G/K是p-超可解的且K=F(G)=Op(G).

設K是G的一個極小正規(guī)子群.由定理假設知G/K是p-超可解的,因為所有p-超可解群組成的群類是一個飽和群系,所以K是G的一個唯一極小正規(guī)子群.由(1)和引理2.2知1≠F(G)=K1×K2×···×Ks,其中Ki(i=1,···,s)是G的一些極小正規(guī)子群.顯然,由K的唯一性有K=F(G),從而得K=F(G)=Op(G).

(3)M/K∈A(p?1),N/K∈A(p?1)且G/K是一個非交換q-群,其中q|p?1.

由(2)知F(M)=K.因為M是超可解的,所以M/K=M/F(M)是交換的.由(1)知 Φ(M)=1,所以由引理2.2,K=A1× ···×Ar,其中Ai(i=1,···,r)是M的極小正規(guī)子群.因M是超可解的,所以對任意的i均有M/CM(Ai)∈A(p?1).于是M/(CM(A1)∩···∩CM(Ar))∈A(p?1).注意到

所以M/K∈A(p?1).同理可得N/K∈A(p?1).

假設|π(G/K)|≠1,令q∈π(G/K)且Q1/K和Q2/K分別是M/K和N/K的Sylowq-子群.由于M/K∈A(p?1),N/K∈A(p?1),所以Q1,Q2是G的正規(guī)超可解子群且(Q1Q2)/K是G/K的一個正規(guī)的Sylowq-子群.因此Q1Q2是G的一個(P1)p-真子群,由G的假設知Q1Q2是超可解的.又因為K=F(G)=F(Q1Q2),于是(Q1Q2)/K是交換的.因此G/K的任意Sylow子群在G/K中均是正規(guī)且交換的,于是G/K是交換群.又因M/K∈A(p?1),N/K∈A(p?1),所以G/K∈A(p?1).由引理2.5知K是循環(huán)的,那么G是超可解的,矛盾.所以|π(G/K)|=1且存在一個素數(shù)q＜p使得G/K是一個q-群.顯然,G/K是非交換的且q|p?1.因此(3)成立.

(4)G是一個P-群.

顯然,G是一個非超可解的P1-群.由(2)和(3),G的任意非平凡商群是超可解的.

另一方面,設A是G的一個P1-真子群.易見,A是G的一個(P1)p-真子群.由G的假設知A是p-超可解的.由于G是p-閉的,所以A也是p-閉的.又因為π(G)={p,q},所以A是超可解的.故G是一個P-群.

(5)得出最后結(jié)論.

由(3),(4)和引理2.1知G同構(gòu)于E(p,q,1),M(p,q,n),Q(p,2)和D(p,2)中的某個群.容易驗證E(p,q,1),M(p,q,n),Q(p,2)和D(p,2)都是Pp-群.定理得證.

定義3.2設A是一個群,如果G存在子群H,K使得HK且K/H≌A,則稱G有一個A-截斷.

推論3.3假設G=MN,其中M,N是G的正規(guī)p-超可解子群.那么G是p-超可解的當且僅當G沒有A截斷,這里A與E(p,q,1),M(p,q,n),Q(p,2)和D(p,2)中的某個群同構(gòu).

命題3.4假設G=MN,這里M,N是G的正規(guī)p-超可解子群.如果π(p?1)∩π(M)∩π(N)=?,那么G是p-超可解的.

證因為G/(M∩N)=M/(M∩N)×N/(M∩N),所以只需證明包含于M∩N的G的pd-主因子均是循環(huán)的即可.令H/K是G的一個包含在M∩N中的pd-主因子.由引理2.6知Op(G/CG(H/K))=1.又因M/K是p-超可解的,所以H/K≤ZU(M/K).由引理2.4,M/CM(H/K)∈GpA(p?1).注意到

且

所以

從而

同理可得

由于π(p?1)∩π(M)∩π(N)=?,所以

因此[MCG(H/K)/CG(H/K),NCG(H/K)/CG(H/K)]=1,從而有G/CG(H/K)∈A(p?1).由引理2.5知H/K是循環(huán)的.所以G是p-超可解的.

定義3.5設p是一個素數(shù),H是一個初等交換p-群.如果|H|=pn,那么記r(H)=n,并且稱H的秩為n.

定理3.6假設G=MN,其中M,N是G的正規(guī)p-超可解子群.設q是π(p?1)∩π(M)∩π(N)的最小素數(shù).如果G的任何包含于M∩N的pd-主因子H/K都滿足r(H/K)＜q,那么G是p-超可解的.

證由命題3.4,不妨假設π(p?1)∩π(M)∩π(N)≠?.假設定理不成立,并設G是使得|G|最小的反例.按照以下步驟得出矛盾:

(1)Φ(G)∩M=Φ(G)∩N=1.

假設上面的斷言之一不成立,即Φ(G)∩M≠1或Φ(G)∩N≠1.不妨假設Φ(G)∩M≠1,令A=Φ(G)∩M.由于M/A∩NA/A=(M∩N)A/A,所以(G/A,M/A,NA/A)滿足定理的假設.由G的選取知G/A是p-超可解的.因此G是p-超可解的,矛盾.

(2)Op′(M)=Op′(N)=1且G是p-閉的可解群.

假定Op′(M)≠1或者Op′(N)≠1,這兩種情況是類似的,所以不妨設B=Op′(M)≠1.通過與(1)相似的討論,知G/B是p-超可解的,由此得G是p-超可解的,矛盾.所以Op′(M)=Op′(N)=1.由引理2.5知p是π(M)和π(N)的最大素數(shù)因子且M,N都是p-閉的超可解子群.因G=MN,所以p是π(G)的最大素因子且G是p-閉的可解群.

(3)K是包含于M∩N的G的唯一極小正規(guī)子群且K=Op(G)=F(M)=F(N).

設K是G的包含于M的極小正規(guī)子群.顯然,(G/K,M/K,NK/K)滿足定理假設,那么由G的選取知G/K是p-超可解的.因此K是G的包含于M的唯一極小正規(guī)子群.由(1)和引理2.2知F(M)=K1×K2×···×Kn,其中Ki(i=1,···,n)是G的極小正規(guī)子群.由K的唯一性知F(M)=K.令H是G的包含于N的極小正規(guī)子群.同理可得G/H是p-超可解的,H是G的包含于N的唯一的極小正規(guī)子群且F(N)=H.顯然,K=H.又因為

所以(3)成立.

(4)設A,B是G的兩個正規(guī)子群且A≤M,B≤N,那么(AB,A,B)滿足定理假設.

如果π(A)∩π(B)=?,由于AB是超可解的,所以(AB,A,B)仍滿足假設條件.因此假設π(A)∩π(B)≠?,令q′是π(A)∩π(B)中的最小的素數(shù).顯然,q′≥q.如果斷言不成立,那么存在AB的一個包含于A∩B的主因子H/K使得r(H/K)≥q′.顯然,A∩B是G的包含于M∩N的正規(guī)子群,所以由Jordan-H?lder定理可知M∩N含有一個G的主因子H′/K′使得r(H′/K′)≥r(H/K)≥q′≥q,而這與定理假設矛盾,所以(4)成立.

(5)M/K∈A(p?1),N/K∈A(p?1)且G/K是一個非交換q-群,其中q|p?1.

由(1),Φ(M)=Φ(N)=1.類似于定理3.1的步驟(3)的證明,有

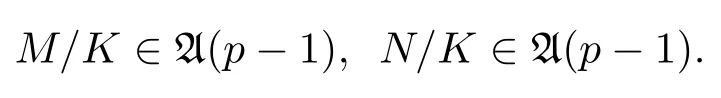
假定|π(G/K)|≥2.設r∈π(G/K)且R1/K,R2/K分別是M/K,N/K的Sylowr-子群.因為M/K,N/K都是交換群且M,N都是超可解群,所以R1≤M,R2≤N是G的兩個超可解正規(guī)子群.記R=R1R2.易見,G≠R且R/K是G/K的正規(guī)的Sylowr-子群.所以由(4)知R是p-超可解的.由引理2.4知R/CR(K)∈GpA(p?1).因為

且Op(G/CG(K))=1,所以

又因為K≤CG(K),所以RCG(K)/CG(K)是G/CG(K)的正規(guī)交換的Sylowr-子群,這就推出G/CG(K)是一個交換群.因此G/CG(K)∈A(p?1).由引理2.5知K是循環(huán)的.因為K是G的正規(guī)Sylowp-子群,所以G是p-超可解的,矛盾.因此|π(G/K)|=1,即存在一個素數(shù)r＜p使得G/K是一個r-群.顯然,G/K是非交換的且r|p?1.

如果r=q,那么(5)成立.假定r≠q.因為π(G)={p,r},所以p=q且p＞r.因此r/∈π(M)∩π(N).又因為G=MN,所以M和N中有一個包含G的某個Sylowr-子群.不妨假設M包含G的某個Sylowr-子群.由(3)知K是G的包含于M∩N的正規(guī)Sylowp-子群,所以G=M,因此G是p-超可解的,矛盾.故(5)成立.

(6)得出最終矛盾.

由(5),π(G)={p,q}且q|p?1.因為K是G的一個包含于M∩N的極小正規(guī)子群,所以由定理假設知r(K)＜q,即|K|＜pq.由(5)和推論3.3知G中存在一個截斷H/J使得H/J同構(gòu)于E(p,q,1),M(p,q,n),Q(p,2)和D(p,2)中的某個群.如果H/J同構(gòu)于Q(p,2)或D(p,2),那么q=2.注意到H/J的Sylowp-子群的階為pq.因為K是G的一個Sylowp-子群,所以|K|≥pq,矛盾.定理得證.

定理3.7假設G=MN,其中M,N是G的正規(guī)p-超可解子群.設q是π(p?1)∩π(M)∩π(N)的最小素數(shù)且P是M∩N的一個Sylowp-子群.如果r(P/Φ(P))＜q,那么G是p-超可解的.

證不妨假設π(p?1)∩π(M)∩π(N)≠?.令q′是

的最小素數(shù),顯然q′≥q.因為

所以POp′(M)/Op′(M)為M/Op′(M)∩NOp′(M)/Op′(M)的一個Sylowp-子群且

于是(G/Op′(M),M/Op′(M),NOp′(M)/Op′(M))滿足定理的假設.對|G|進行歸納知G/Op′(M)是p-超可解的,因此G是p-超可解的.所以不失一般性,可以假設Op′(M)=1或Op′(N)=1.由引理2.3知M,N均是p-閉的.因此PG,于是Φ(P)G.由于r(P/Φ(P))＜q,所以(G/Φ(P),M/Φ(P),N/Φ(P))滿足定理3.6的假設.注意:如果

仍然認為(G/Φ(P),M/Φ(P),N/Φ(P))滿足定理3.6的假設.所以對|G|進行歸納有G/Φ(P)是p-超可解的,從而知G是p-超可解的.

推論3.8假設G=MN,其中M,N是G的正規(guī)超可解子群.若對任意的p∈π(M∩N),令q是π(p?1)∩π(M)∩π(N)的最小素數(shù),如果對于G的任意包含于M∩N的pd-主因子H/K均有r(H/K)＜q,那么G是超可解的.

推論3.9假設G=MN,其中M,N是G的正規(guī)超可解子群.若對任意的p∈π(M∩N),令q是π(p?1)∩π(M)∩π(N)的最小素數(shù),如果P是M∩N的一個Sylowp-子群且滿足r(P/Φ(P))＜q,那么G是超可解的.

[1]湯興政.有限群的超可解性和關(guān)于正規(guī)超可解群的積的一些問題[D].合肥:中國科學技術(shù)大學,2016.

[2]Guo Wenbin.Structure theory for Canonical classes of finite groups[M].Berlin:Springer,2015.

[3]Arroyo-Jordá M,Arroyo-Jordá P,Martínez-Pastor A,Pérez-Ramos M D.On finite products of groups and supersolubility[J].J.Alg.,2010,323:2922–2934.

[4]Asaad M,Shaalan A.On the supersolvability of finite groups[J].Arch.Math.,1989,53(4):318–326.

[5]Baer R.Classes of finite groups and their properties[J].Illinois J.Math.,1957,1:115–187.

[6]Ballester-Bolinches A,Pérez-Ramos M D,Pedraza-Aguilera M C.Mutually permutable products of finite groups[J].J.Alg.,1999,213(1):369–377.

[7]Friesen D R.Products of normal supersolvable subgroups[J].Proc.Amer.Math.Soc.,1971,30(1):46-48.

[8]Guo Webin,Kondrat’ev A S.Finite minimal non-supersolvable groups decomposable into the product of two normal supersolvable subgroups[J].Commun.Math.Stat.2015,3(2):285–290.

[9]Guo Webin,Shum K P,Skiba A N.X-quasinormal subgroups[J].Sib.Math.J.,2007,48(4):593–605.

[10]Guo Wenbin,Skiba A N.On quasisupersoluble andp-quasisupersoluble finite groups[J].Alg.Coll.,2010,17(4):549–556.

[11]Guo Wenbin,Kondrat’ev A S.New examples of finite non-supersolvable groups factored by two normal supersoluble subgroups[J].International Conference“Mal’tsev meeting”Collection of Abstracts,p.92.Sobolev Institute of Mathematics,Novosibrisk:Novosibirsk State University,2012,12–16.

[12]Guo Wenbin,Skiba A N.On the intersection of the F-maximal subgroups and the generalized F-hypercentre of a finite group[J].J.Alg.,2012,366:112–125.

[13]Huppert B.Monomiale darstellung endlicher gruppen[J].Nagoya J.Math.,1953,6:93–94.

[14]查明明,郭文彬,李保軍.關(guān)于有限群的p-超可解性[J].數(shù)學雜志,2007,27(5):562–568.

[15]Guo Wenbin.The theory of classes of groups[M].Beijing,New York:Science Press;Kluwer,Academic Publishers,2000.

[16]Ballester-Bolinches A,Esteban-Romero R,Asaad M.Products of finite groups[M].Berlin,New York:Walter de Gruyter,2010.

[17]Weinstein M.Between nilpotent and solvable[M].Passaic,New York,Jersey:Polygonal Publishing House,1982.

THE PRODUCT OF TWO NORMALP-SUPERSOLUBLE SUBGROUPS

MAO Yue-mei1,2,MA Xiao-jian1,TANG Xing-zheng2
(1.Institute of Quantum Information Science,Shanxi Datong University,Datong 037009,China)
(2.School of Mathematical Sciences,University of Science and Technology of China,Hefei 230026,China)

In this paper,we study the stucture of minimal non-p-supersoluble groups which are the product of two normalp-supersoluble subgroups.By using basic methods of finite group theory,some sufficient conditions under which the product of two normalp-supersoluble subgroups is stillp-supersoluble are obtained.Meanwhile,some results in[1]about supersoluble groups can be generalized.

finite groups;supersoluble groups;p-supersoluble groups;Sylow subgroups

20D10;20D15;20D20

O152.1

A

0255-7797(2017)06-1309-08

2016-05-27接收日期:2016-09-05

國家自然科學基金(11371335).

毛月梅(1980–),女,山西大同,博士,主要研究方向:群論.