A scheme for Sagnac-effect quantum enhancement with Fock state light input?
Kun Chen(陳坤),Shu-Xin Chen(陳樹新),De-Wei Wu(吳德偉), Chun-Yan Yang(楊春燕),and Qiang Miao(苗強)
Information and Navigation College,Airforce Engineering University,Xi’an 710077,China
A scheme for Sagnac-effect quantum enhancement with Fock state light input?
Kun Chen(陳坤),Shu-Xin Chen(陳樹新)?,De-Wei Wu(吳德偉), Chun-Yan Yang(楊春燕),and Qiang Miao(苗強)
Information and Navigation College,Airforce Engineering University,Xi’an 710077,China
Sagnac effect enhancement can improve optical gyro precision.For a certain input intensity,we suggest that the other input port of beam splitter(BS)should be fed with some quantum light to break through shot noise limit(SNL)to improve Sagnac effect without increasing radiation-pressure noise(NRP).We design a Sagnac effect quantum enhancement criterion (SQEC)to judge whether some quantum light can enhance Sagnac effect and present a Sagnac effect enhancement scheme that utilizing Fock state light and parity measurement technique to extract the output phase.The results of the theoretical analysis show that the maximum sensitivity can be reached at θ=0,and the phase precision can break through SNL and even achieve Heisenberg limit(HL).When the Fock state average photon number n is far less than coherent state,the minimum measurable angular rate is improved withtimes,which can deduce shot noise and increase NRP little.
optical gyro,radiation-pressure noise,parity measurement,Heisenberg limit
1.Introduction
The enhancement scheme of Sagnac effect which is the physical basis of gyroscope,is an interesting topic for the improvement of gyroscope precision.[1–4]Many melioration schemes have been proposed via atoms[5–7]and trapped ions.[8,9]In optical regime,the optical gyroscope fed with laser in coherent states,[10]of which the phase sensitivity is restricted by shot noise limit(SNL)whereis the total mean photon number in the interferometer.The gyroscope precision can be improved mainly by increasing the laser power(increasing),whereas radiation-pressure noise(NRP)will dominate and nonlinear effects will be introduced.[12]An effective method is to improve the precision under a certain source power.
Quantum metrology pointed out that some entanglement properties of input states(N00N state,twin-Fock state,Yurke state,etc.)can be used to break through SNL and even reach the fundamental limit,[13]Heisenberg limit(HL),showing a new way to improve gyroscope precision with quantum techniques.Bertocchi et al.firstly studied Sagnac quantum effect at the single-photon level whose results are no below SNL due to that there is no entanglement in the input states.[14]Kolkiran et al.obtained the HL by entering two-photon entangled states generated via parametric down-conversion.However,in such technical applications,high intensity sources are needed.[15]Caves suggested that sub-shot noise uncertainty can be achieved when a high-intensity coherent state in one input port and the other input port fed with a low-intensity squeezed vacuum state in an interferometer.[16]We utilized the squeezed vacuum light and quantum balanced homodyne detection technique to improve the phase precision obviously[17]and further discussed the optimal measurement method for the coherent state and the squeezed vacuum state in the Sagnac interferometer.[18]However,the squeezed vacuum technique cannot achieve the highest sensitivity at θ=0 unless introducing phase biasing technique.In this paper,we discuss whether there are other useful states in the other input port which can obtain sub-shot-noise phase sensitivity.We design a Sagnac effect quantum enhancement criterion(SQEC)to judge whether a quantum state is useful and develop a Fock state scheme for Sagnac effect enhancement.
This manuscript is organized as follows.In Section 2, we make a theoretical description for Sagnac effect and design the SQEC based on quantum Fisher information(QFI). In Section 3,we use the SQEC to judge some common quantum states,such as coherent state,Fock state,squeezed vacuum state,and coherent superposition state.In Section 4,we present a Sagnac effect enhancement scheme with Fock state light input and parity measurement technique to extract the output phase.In Section 5,we make an analysis of the scheme. Finally,we discuss the physics underlying phase sensitivity improvement with Fock state light and draw a conclusion.
2.Sagnac effect quantum enhancement criterion
Due to the phaseθ precision restricted with shotnoise,for the improvement of measurement precision,we suggest thatthe other input port should be fed with some quantum light. We make a brief theoretical description for Sagnac effect,and then design the SQEC to judge whether a quantum state is useful.
2.1.Theoretical description for Sagnac effect
Sagnac effect was first proposed by Georges Sagnac in 1913 for rotation detection in inertial space with optical systems.[19]As illustrated in Fig.1,if Sagnac interferometer rotates with an angular rate ? along the clockwise direction, the two parts of light split at point A will take different time for a circle along clockwise and anti-clockwise direction separately and the time difference is Δt=4πr2?/c2(λ is wavelength,r is the radius of interferometer,and c is the speed of light).Accordingly,the optical path difference is
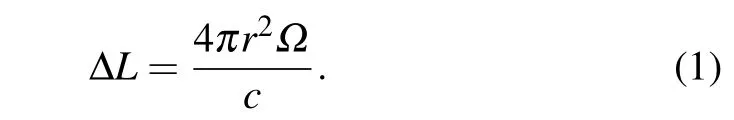
Furthermore,we can obtain a linear relation between the relative phase θ and rotation rate ? as[20]

where L is the optical path length.The accuracy of rotating rate ? depends on the measurement precision of phase θ.Therefore,Sagnac effect enhancement is to improve the precision of phase θ essentially.
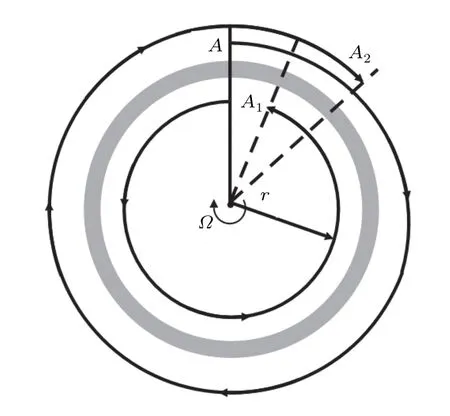
Fig.1.A schematic diagram of Sagnac effect.[17]
Next,we describe the Sagnac effect in the Schwinger representation with quantum theory.[21]When the two input quantum states|in〉inject into the input ports P1and P2of the Sagnac interferometer depicted in Fig.2 respectively, they are both split into two beams by the beam splitter(BS) and mix with each other.The state upon leaving the BS is |?〉=exp(?iπ/2Jx)|in〉where Jx≡(a+b+b+a)/2 is an angular momentum operator.The quantum state|?〉accumulates a relative phase θ due to the interferometer rotation and becomes|?′〉=exp(?iθJz)|?〉where Jz≡(a+a?b+b)/2. |?′〉joins at the BS and leaves the interferometer.The output state is|out〉=exp(iπ/2Jx)|?′〉.We can obtain the relationship between input and output states as
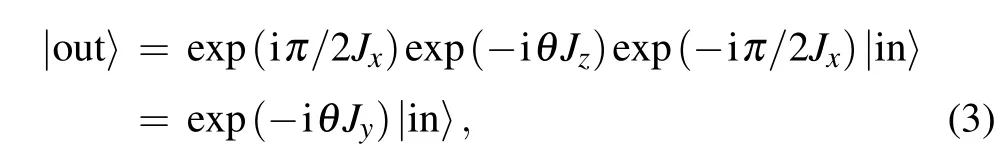
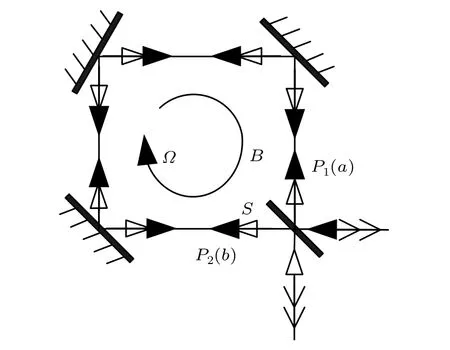
Fig.2.A schematic diagram of Sagnac interferometer.
2.2.SQEC design
The current optical gyro is fed with coherent light into one input port of BS and detected at another output port.In fact,the other input port is fed with vacuum instead of nothing, which restricts the phase precision at the SQL theoretically,as shown below.
When the Sagnac interferometer shown in Fig.2 has two input ports injected with quantum states,the relationship between input and output ports in Eq.(3)can be written in a density matrix as
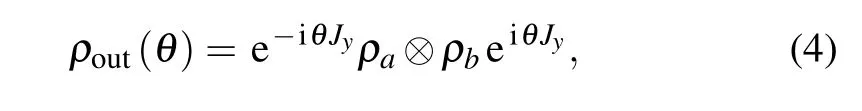
where ρaand ρbare density operators of the quantum state entering into input ports P1and P2,respectively.The estimation precision of phase θ can be described with quantum Cramer–Rao bound(QCR)[22]
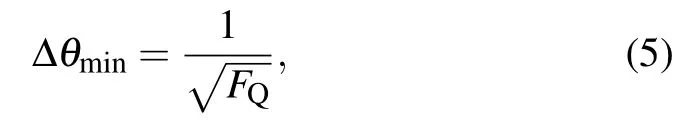
where FQis the so-called QFI,which can be calculated by maximizing the Fisher information over all possible positive operator valued measures(POVM)[23]
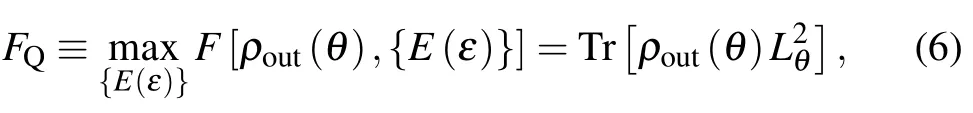
where{E(ε)}are a set of Hermitian positive-operators and Lθis the Hermitian operator of symmetric logarithmic derivative (SLD),defined as
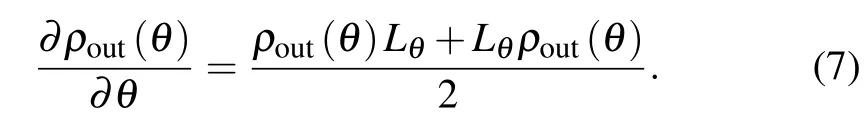
If ρaand ρbare pure states,we can obtain the relation ρout(θ)=ρout(θ)2from Eq.(4),of which the derivative of θ is?θρout(θ)=?θρout(θ)2=[?θρout(θ)]ρout(θ)+ ρout(θ)[?θρout(θ)].Comparing with Eq.(7)of the SLD def inition,we have
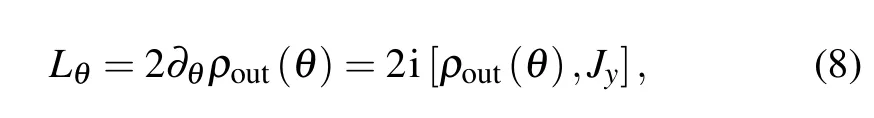
and then
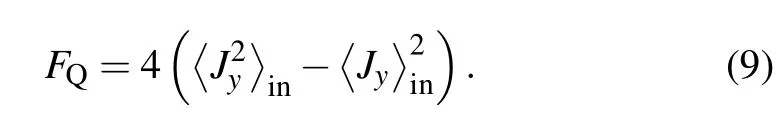
With further calculation,we can obtain the QFI
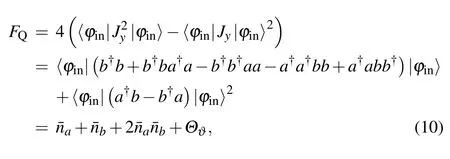
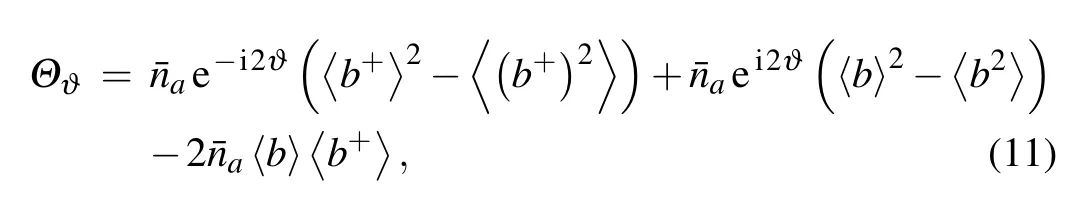
In the system,the total photon number,the SNL and HL are defined respectively as

Substituting Eq.(10)into Eq.(5)and comparing with Eq.(12),we can obtain the SQEC,namelyIf SQEC is satisfied,the phase precision can break through SNL and Sagnac effect can be enhanced with certain light power.If one conditionis satisfied,HL can be achieved.If only one quantum state enters into the interferometer,whatever ρaor ρb,it is easy to verify that the system can only achieve SNL.This agrees with the conclusion of Caves that if only one quantum state enters into the BS,the other input port will introduce vacuum fluctuation restricting the parameter estimation precision.
3.SQEC analysis of quantum states
In order to improve the Sagnac phase accuracy and break through SNL with a fixed total photon number,we need to choose a suitable quantum state entering the input port b to satisfy SQEC and make Θ?as large as possible.We will make an analysis of some common quantum states such as coherent state,Fock state,squeezed vacuum state,and coherent superposition state,which can be produced in experiment.
3.1.Coherent state|β〉
If coherent state|β〉fed into the input port P2,where β= |β|e?i?β,we can obtainandwhich does not satisfy SQEC.It can be found that QFI cannot be improved by entering a coherent state into the other port. Therefore,the coherent state cannot enhance the Sagnac effect.
3.2.Fock state|n〉
The Fock state,also known as the photon number state,is in extensive research for quantum metrology which can be produced through parametric down-conversion in experiment.[24]If port P2fed with Fock state|N〉,we obtain Θ?=0 andwhich suggests that the Fock state in port b can improve QFI.If the power of coherent state|α〉is much higher than Fock state|N〉,namelywe getand the phase precisionwhich means that the phase precision increases effectively as the photon number of Fock state increases.
3.3.Squeezed vacuum state|ξ〉
The squeezed vacuum state has been extensively studied in quantum communication,gravitational wave detection, and precision measurement due to that the quantum fluctuation of a quadrature component is smaller than vacuum fluctuation,and can be produced through a parametric amplifier or a four-wave mixing experimentally.[25]If port P2fed with squeezed vacuum state|ξ〉,we getandwhich satisfy SQEC and the precision increases with the squeezed strength r exponentially.In particular,owing towhen,we obtainandwhich reaches HL.It is obvious that the squeezed vacuum state can enhance Sagnac effect effectively, which have been discussed in detail in Ref.[17].
3.4.Coherent superposition state
The coherent superposition state|αb〉,or Schrodinger cat state,is defined as[26]
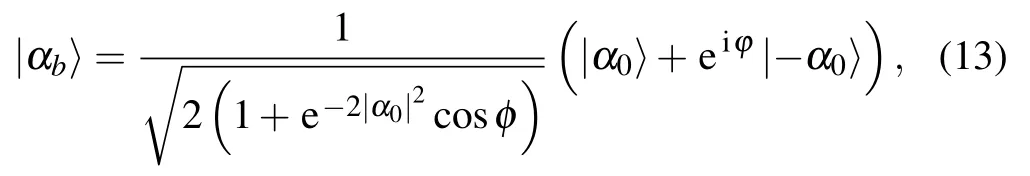
where|αb〉is called even coherent state when φ=0;when φ=π/2,|αb〉is called Yurke–Stoler coherent state;when φ=π,|αb〉is called odd coherent state.Without loss of generality,we take α0as a real number.When selecting the optimal phase matching condition ?=π/2,we have
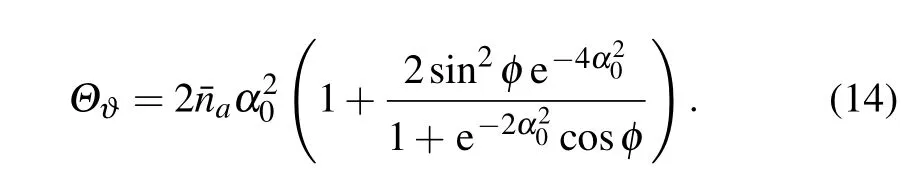
When|αb〉is the odd or even coherent state,Θ?=When|αb〉is the Yurke–Stoler coherent state,Θ?=When,we can obtain≈and
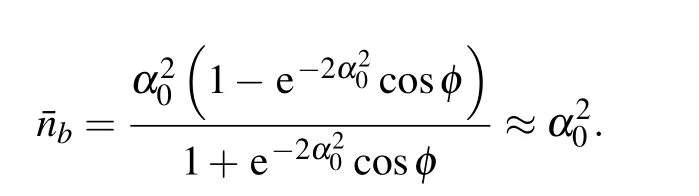
When the coherent superposition state is fed into the input port P2,the sub-shot-noise uncertainty can be approached and the QFI isIn particular,whenwe havewhich means that the coherent superposition state can also achieve an HL-like squeezed vacuum state.The coherent superposition state is also a kind of macroscopic superposition states,which is conducive to enhance the Sagnac effect in experiment.
Through the analysis above,the other input port of Sagnac BS fed with some quantum light in Fock state, squeezed vacuum state,or coherent superposition state can break through SNL and increase phase precision to a certain degree in theory.Here,we choose Fock state light to enter into the BS for Sagnac effect enhancement(the enhancement scheme based on coherent superposition state input will be published elsewhere).Nevertheless,the QCR and SQEC are obtained based on POVM,which is a difficult task for design in experiment.How to design a POVM or implement optimal measurement to reach QCR experimentally is still an open question.The key problem is how to effectively extract the phase information of the output light.Parity measurement technique is suggested as follows.
4.Parity measurement for Fock state input
In the Sagnac effect enhancement scheme with Fock state light inputas shown in Fig.3,coherent state|α〉and Fock state |N〉respectively enter into the input ports P1and P2of BS.As the BS will be used twice as input and output,we set an optical circulator under port P2for input and output isolation.
Parity measurement technique was firstly put forward by Bollinger et al.for spectrum measurement,and then introduced into the optical interferometry.[27]As experimenters only need to measure the parity of the photon number at one of the output ports,parity measurement is easy for manipulation. For any mode a,the parity operator can be expressed as[28]
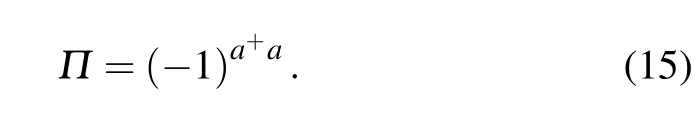
Generally,it is difficult to calculate parity operator expectation〈Π〉directly.As the expectation〈Π〉is proportional to the value of the Wigner function of output quantum state at the origin of the phase space,it can be obtained by calculating the Wigner function of the output state.
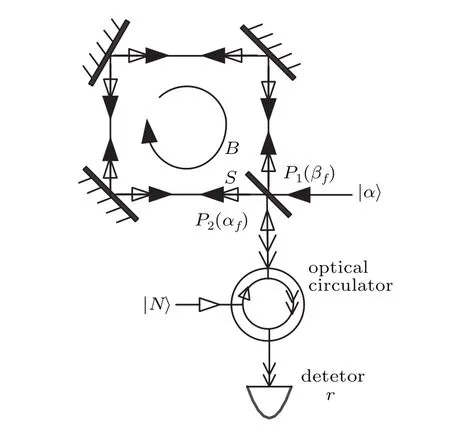
Fig.3.Sagnac effect enhanced scheme.
The Wigner function of the input state ρa?ρbin Eq.(4) is the product of two Wigner functions of ρaand ρb[29]
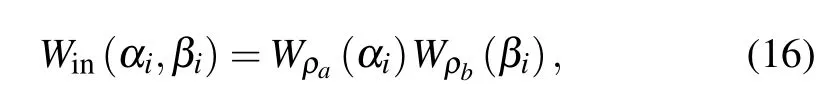
where Wρa(αi)and Wρb(βi)are Wigner functions of input state ρaand ρbrespectively.When ρaand ρbare coherent state and Fock state,there are

where the Laguerre polynomials Ln(·)is written in the form of its generation function[30]
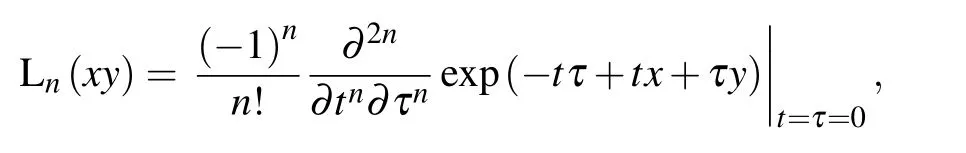
for convenient calculation later.For the two output ports αfand βfin the interferometer,substituting the input and output relation[31]
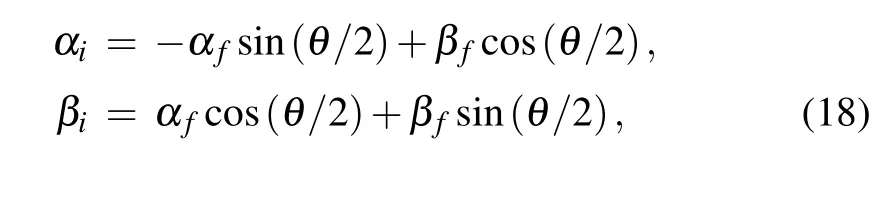
and Eq.(17)into Eq.(16),we can obtain the Wigner function of the output state as

As we measure the photon number parity at the output port af,the origin of the Wigner function value of output state of port afis needed.Integrating βfof Eq.(19)and setting αf=0,we can obtain
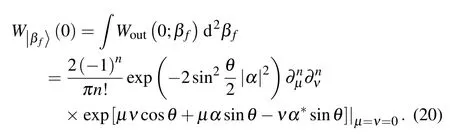
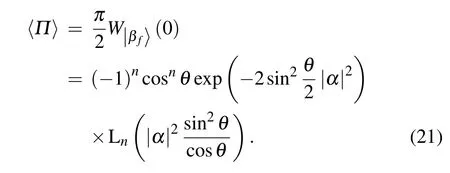
In Eq.(21),when θ→0,〈Π〉→(?1)nwhich corresponds to the parity operator expectation of Fock state and indicates that the output is Fock state without coherent state;when θ→π,which corresponds to parity operator expectation of coherent state and indicates that the output is coherent state without Fock state.This can be understood that the output state is the statistical mixture between Fock state and coherent state modulated by the relative phase θ.
When cosθ=0(θ=π/2 or 3π/2),the parity operator expectation is
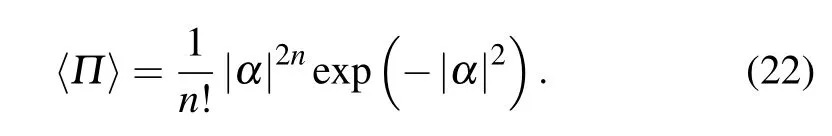
The parity operator expectation with different average photon numbers of Fock state is shown in Fig.4,where the average photon number of coherent state is|α|2=2.The peak of parity operator expectation is at θ=0,at which we can reach the highest sensitivity.When Fock state injectsinto the Sagnac interferometer,even if there is only one photon,the wave crest becomes steeper,which indicates that the phase sensitivity has been improved effectively.Figures 4(b)and 4(c)respectively describe the relationships between parity operator expectation and the average photon number n of Fock state which changes from 0 to 20.It can be clearly found that the wave crest becomes steeper and steeper as n increases.Next to the wave crest,the expectation curve exists a fluctuation and then is relatively stable in a rather long phase scope(Fig.4(c)).The sensitivity of wave crest and wave trough increase as n increases, and there is more large angle range with low sensitivity.In the next section,theory analysis is given.
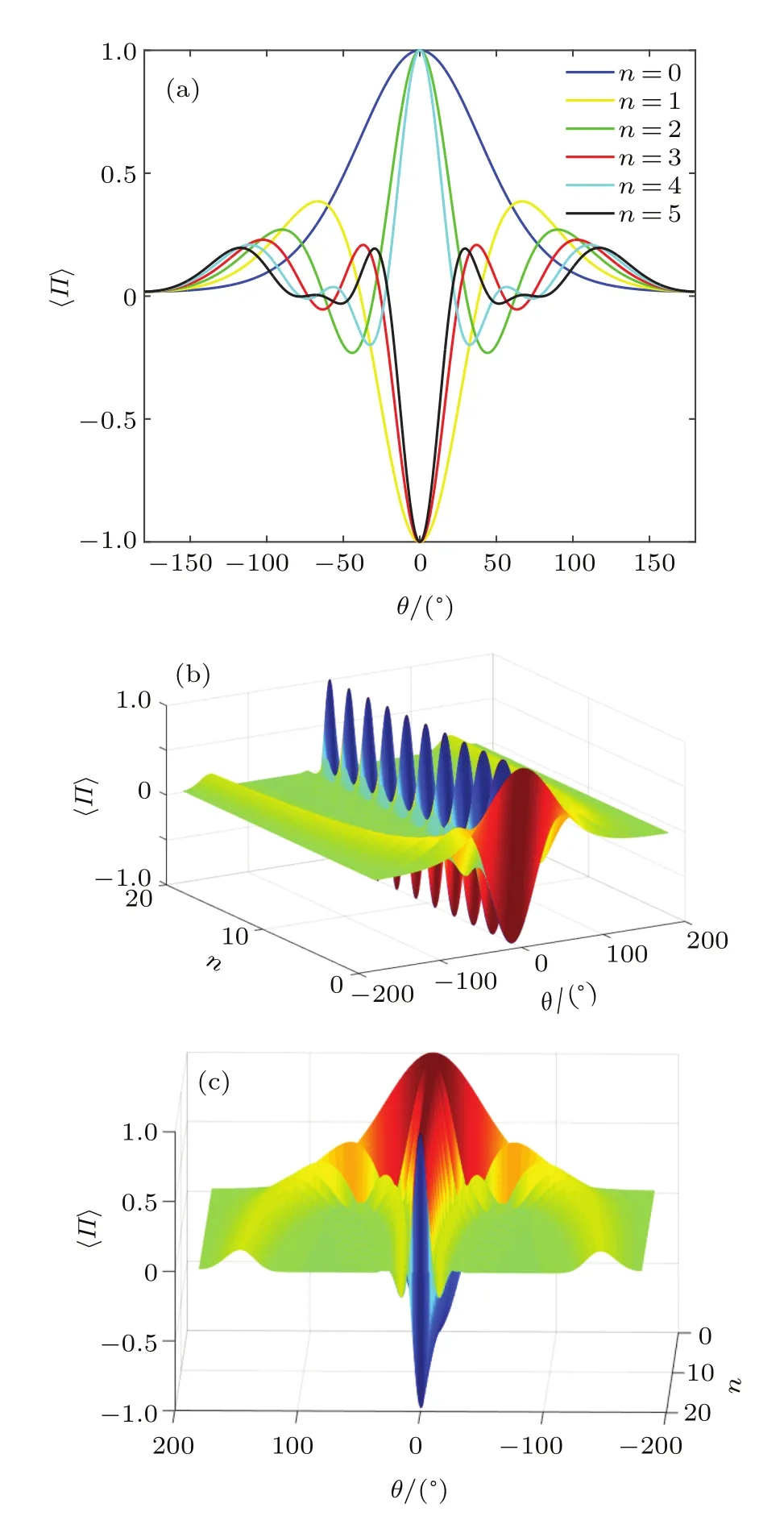
Fig.4.(color online)Parity operator expectation against phase θ for different mean photon numbers of Fock state n(the mean photon number of coherent state|α|2=2).(a)The curve of parity operator expectation for different n;(b)the three-dimensional(3D)plot of parity operator expectation against phase θ as n increases;(c)the 3D plot of parity operator expectation against phase θ as n decreases.
5.Performance analysis
As the laguerre polynomials can be written as

which can achieve QCR and indicate the phase with the highest sensitivity at θ=0.Although the error achieves QCR, showing that the parity measurement is a kind of optimal measurement method,we cannot break through SNL without Fock state input,as shown in Fig.5.

Fig.5.(color online)The curve of phase error with only coherent light input.
When n≥1,the derivative of parity operator expectation is
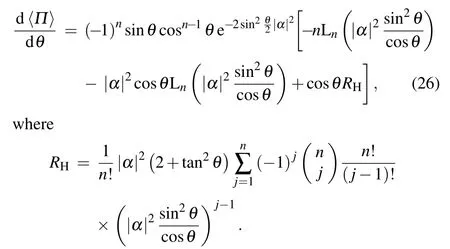
If there is only Fock state input,namely|α|2=0,the parity operator expectation is〈Π〉=(?1)ncosnθ and its derivative is d〈Π〉/dθ=?(?1)nn cosn?1θ sinθ.We can obtain the phase error
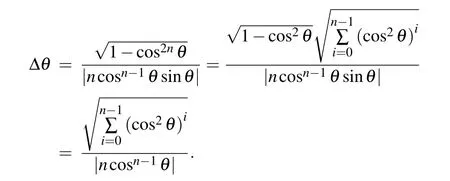
When θ→0 or θ→π,Δθ can reach QCR,as shown in Fig.6.We cannot break through the SNL only with Fock state input either.
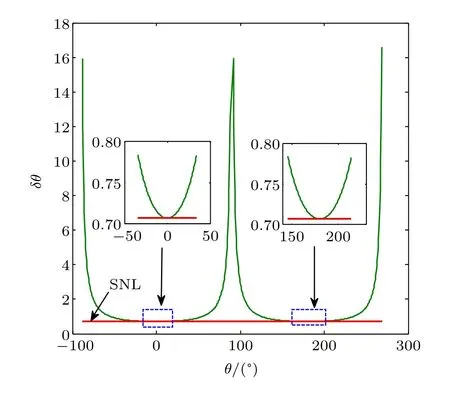
Fig.6.(color online)The curve of phase error with only Fock state light input.
When|α|2>0,the phase error with both Fock state and coherent state input is
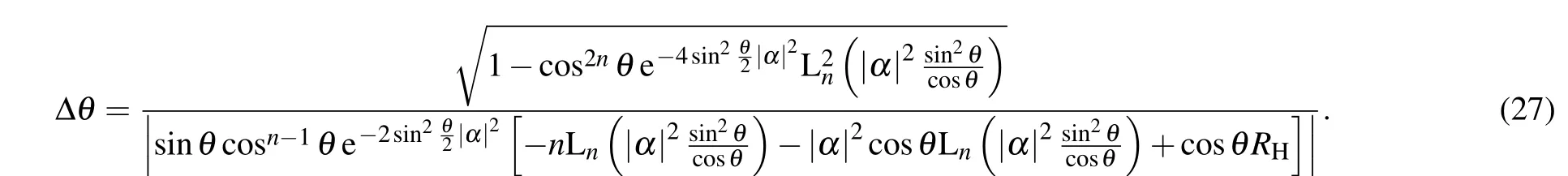
When θ→0,the minimum error can be obtained as
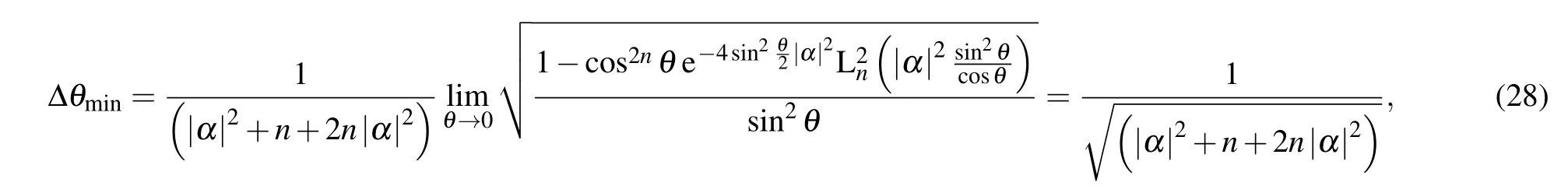
which suggests that the best sensitivity is at θ→0 and parity measurement can achieve HL as shown in Fig.7.Because the denominator of Eq.(27)will become 0 at several values of θ as the photon number n changes,some errors become large and several peaks emerge in the error curve,which means that the performance of this method is poor at some values of phase. The error curve is relatively flat near 0°,and reaches the minimum at 0°.To facilitate the analysis of the minimum error, we draw the error curve near 0°area as shown in Fig.7(b), where n=1.It can be found that the error indeed reaches HL which proves the validity of Eq.(28).The proposed scheme can reach the highest sensitivity when θ→0 directly.

Fig.7.(color online)Phase errors of coherent state and Fock state input (the mean photon number of coherent state|α|2=2).(a)The phase error at different values of θ and mean photon number of Fock state; (b)the phase error curve near 0°area.
The analysis above indicates that parity measurement technique is a feasible and optimal method to reach QCR and break through SNL.As a result of the Fock state input, compared with only increasing the pure coherent light photon number(power),one extra item 2n|α|2emerges in the denominator of Eq.(28),which is the key role to improve the phase accuracy under the same power,as shown in Fig.8.
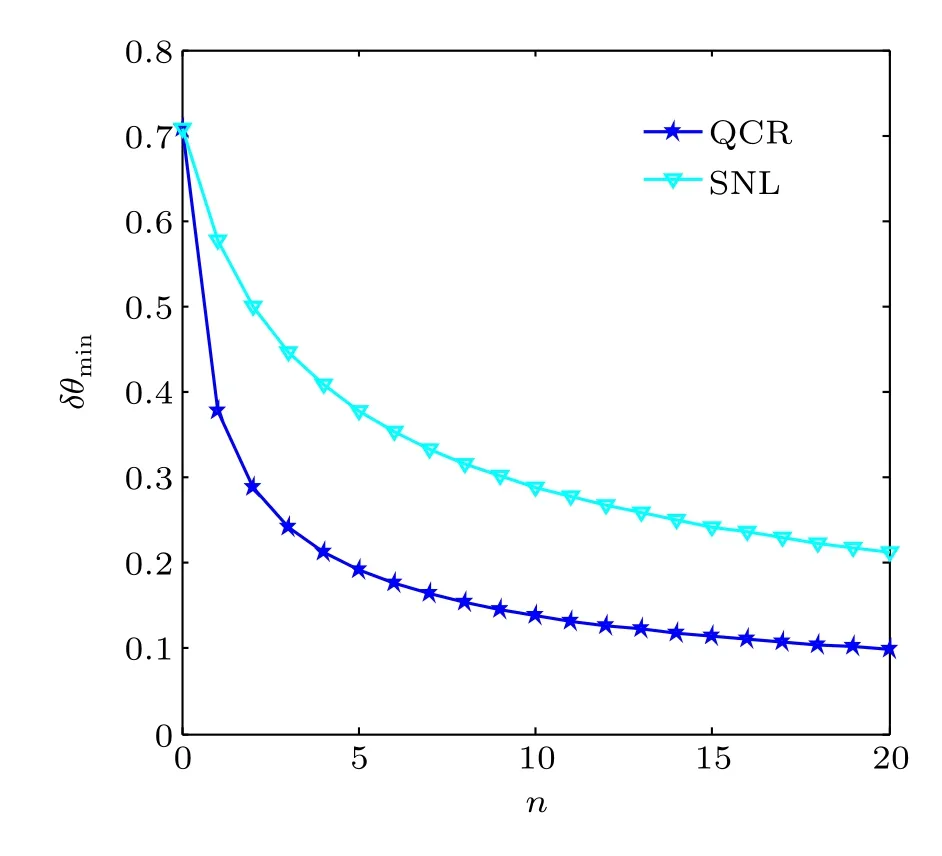
Fig.8.(color online)The phase error comparison between suggested scheme and SNL.
Specifically,we take the fiber optic gyro(FOG)for example to discuss the performance with this technique as follows. The measurable minimum angular rate is a very important indicator.Usually,the best phase sensitivity corresponds to the measurable minimum angular rate
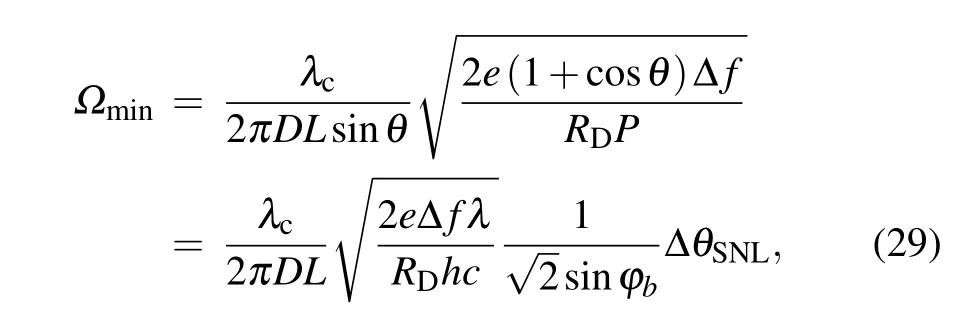
where h is the Planck constant,e is electron energy,and c is the speed of light.For a FOG of the wavelength λ= 1550 nm,the length of optical fiber L=5 km,coil diameter D=0.2 m,detector responsivity PD=1 A/W,signal bandwidth Δf=0.01 Hz,the optical power P=250μW,and phase bias ?b=3π/4.We can obtain the minimum detectable angular rate ?min=4.2×10?5(°)/h with the first equation.
When the mean photon number of coherent state and Fock state respectively are|α|2and n,the phase SNL isCombining with Eqs.(28)and(29),we have
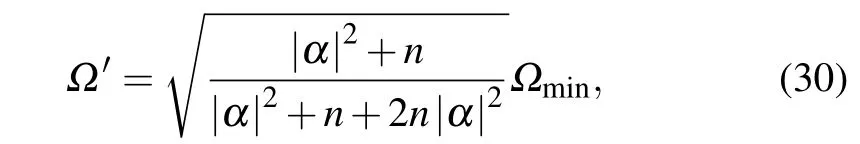
where ?′can reach the minimum valuewhen|α|2=n.If the optical power P=250μW,according to the formula P=hcn/λ,the average photon number is 1.9×1015approximately and n=9.5×1014.We can calculate the minimum detectable angular rate in the proposed schemewhich is enhanced 7 orders without any input power increase.
The dynamic range of FOG is the ratio of the maximum input angular rate to the minimum angular rate.The dynamic range of the classical method can achieve π/Δ?SNL,and this proposed method can increasetimes,which shows that the dynamic range is increased with the square root of the average photon number of Fock state.
Although it is difficult to make the power of Fock state equal to coherent state,the precision of gyro can be improved under the same power by entering the Fock state into the interferometer.When the Fock state average photon number is far less than that of coherent state,there iswhich means that the minimum detectable angular rate can be improved with a factor ofFor example,as long as the input Fock state average photon number reaches 50,the accuracy can be improved with 10 times while NRP increases little.
6.Discussion
What is the essential physics for phase sensitivity improvement in the interferometer?In the Sagnac linear interferometer,it is the particle entanglement of input states that provide sub-shot-noise phase uncertainty.Pezze pointed out that not all the entangled states can overcome SNL,but the one,and only one,which satisfied with the sufficient condition for entanglement judgeIf the sufficient condition is satisfied,the input states ρinare entangled and can achieve the sub-shot-noise phase uncertainty Δθmin=suggesting ρinare useful for Sagnac effect enhancement.When the input states are coherent state ρaand Fock state|N〉,we can calculate the QFI of input states ρin=ρa?|N〉〈N|and obtainindicating that the input states are in entangled states and can overcome SNL.The squeezed vacuum state and coherent superposition state mentioned above can both be in the useful entangled states with coherent state.
In particular,when passing through the BS,the quantum states ρin=ρa?|N〉〈N|are transformed as
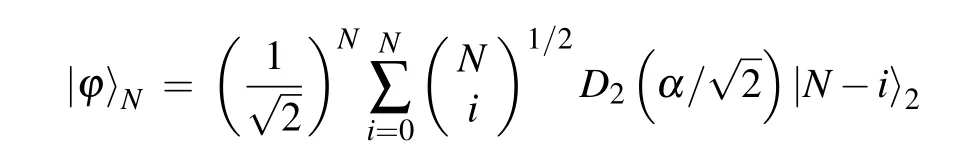

where D(α)=exp(αa+?α?a)is the displacement operator. It is easy to find that|?〉Nhas strong correlations between the displaced Fock states of the two modes,[33]which is similar to the macroscopic maximally entangled state,entangled coherent state.The distinction is that the entangled coherent state is entangled between coherent state and vacuum state,as|?〉Nis statistical mixture with the entangle states between displaced Fock states.When entering a Fock state with only one photon, equation(31)can be simplified as
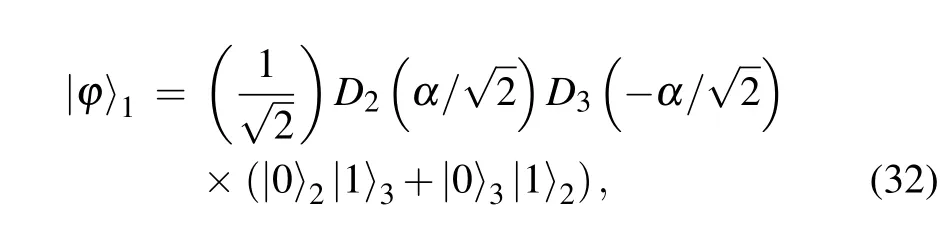
which is entangled between coherent state(displaced vacuum state)and displaced Fock state.It is the one input photon that produces an entangled state with large photon numbers, which is the physical reason why 2.4 dB sensitivity gain can be achieved with only one photon injection.
If the other input port fed with coherent state|β〉, the input quantum states|α〉|β〉will be transformed intoafter the BS,which is direct product state of two coherent states but not entangled.This is distinct from Fock state input.Obviously,coherent state is not able to increase phase sensitivity,which is consistent to the conclusion of SQEC.
Through the analysis above,the most important reason for Sagnac effect enhanced with Fock state input is that the quantum states after BS in two modes are entangled,which can provide sub-shot-noise phase sensitivity with appropriate measurement method at the output.
7.Conclusions
We design a SQEC to judge whether the quantum light can enhance Sagnac effect and present a Sagnac effect enhancement scheme by utilizing Fock state light and parity measurement technique to extract the output phase.The results of the theoretical analysis show that the maximum sensitivity can be reached at θ=0,and the phase precision can break through SNL and even achieve Heisenberg limit(HL). When the Fock state average photon number n is far less than that of coherent state,the minimum measurable angular rate is improved withtimes,which can deduce the shot noise and increase NRP little.We can achieve much higher accuracy with a relative small power of Fock state input.The proposed scheme is an effective way to improve the precision of gyro.
[1]Joseph S 2014 Gen.Relativ.Gravit.46 1710
[2]Jing J,Li Y,Zhang Z C,Wu C X and Song N F 2016 Chin.Phys.B 25 084213
[3]Wu Q,Yu J L,Wang J,Wang W R,Jia S,Huang G B,Hei K F and Li L J 2015 Acta Phys.Sin.64 044205(in Chinese)
[4]Liu J,Zhang T E,Zhang W,Lei L H,Xue C Y,Zhang W D and Tang J 2015 Acta Phys.Sin.64 107802(in Chinese)
[5]Luo C,Huang J,Zhang X and Lee C 2017 Phys.Rev.A 95 023608
[6]Gauguet A,Canuel B,Leveque T,Chaibi W and Landragin A 2009 Phys.Rev.A 80 063604
[7]Tackmann G,Berg P,Schubert C,Abend S,Gilowski M,Ertmer W and Rasel E M 2012 New J.Phys.14 015002
[8]Rico-Gutierrez L M,Spiller T P and Dunningham J A 2015 New J. Phys.17 043022
[9]Campbell W C and Hamilton P 2016 arXiv:1609.00659
[10]Schreiber K U,Klugel T,Wells J P R,Hurst R B and Gebauer A 2011 Phys.Rev.Lett.107 173904
[11]Giovanetti V,Lloyd S and Maccone L 2011 Nat.Photon.5 222
[12]William N P and Jonathan P D 2010 New.J.Phys.12 083014
[13]Xiang G Y and Guo G C 2013 Chin.Phys.B 22 110601
[14]Bertocchi G,Alibart O,Ostrowsky D B,Tanzilli S and Baldi P 2006 J. Phys.B 39 1011
[15]Kolkiran and Agarwal G S 2007 Opt.Express 15 679
[16]Caves C M 1981 Phys.Rev.D 23 1693
[17]Chen K,Chen S X,Wu D W,Yang C Y and Wu H 2016 Acta Phys.Sin. 65 054203(in Chinese)
[18]Chen K,Chen S X,Wu D W,Yang C Y,Wang X,Li X,Wu H and Liu Z W 2016 Acta Phys.Sin.65 194203(in Chinese)
[19]Barrett B,Geiger R and Dutta I 2014 C.R.Physique 15 875
[20]Scully M O and Zubairy M S 1997 Quantum Optics(Cambridge:Cambridge University Press)pp.101–106
[21]Yurke B,McCall S L and Klauder J R 1986 Phys.Rev.A 33 4033
[22]Alex M 2006 Phys.Rev.A 73 033821
[23]Luca P and Augusto S 2014 arXiv:1411.5164v1[quant-ph]
[24]Luca P and Augusto S 2013 Phys.Rev.Lett.110 163604
[25]Baune C,Gniesmer J,Sch?nbeck A,Vollmer C E,Fiurasek J and Schnabel R 2015 Opt.Express 23 16035
[26]Jaewoo J,Kimin P,Hyunseok J,William J M,Kae N and Timothy P S 2012 Phys.Rev.A 86 043828
[27]Gerry C C 2000 Phys.Rev.A 61 043811
[28]Campos R A,Gerry C C and Benmoussa A 2003 Phys.Rev.A 68 023810
[29]Hu L Y,Wei C P,Fang J,Huang J H and Liu C J 2014 Opt.Commun. 323 68
[30]Xu X F and Fan H Y 2015 Chin.Phys.B 24 010301
[31]Tan Q S,Liao J Q,Wang X G and Franco N 2014 Phys.Rev.A 89 053822
[32]Luca P and Augusto S 2009 Phys.Rev.Lett.102 100401
[33]Windhagera A,Suda M,Pacher C,Peev M and Poppe A 2011 Opt. Commun.284 1907
19 December 2016;revised manuscript
23 May 2017;published online 2 August 2017)
10.1088/1674-1056/26/9/094212
?Project supported by the National Natural Science Foundation of China(Grant Nos.61573372 and 61603413).
?Corresponding author.E-mail:chenshuxin68@163.com
?2017 Chinese Physical Society and IOP Publishing Ltd http://iopscience.iop.org/cpb http://cpb.iphy.ac.cn
- Chinese Physics B的其它文章
- Relationship measurement between ac-Stark shift of 40Ca+clock transition and laser polarization direction?
- Air breakdown induced by the microwave with two mutually orthogonal and heterophase electric field components?
- Collective motion of active particles in environmental noise?
- Temperature dependence of heat conduction coefficient in nanotube/nanowire networks?
- Analysis of dynamic features in intersecting pedestrian flows?
- Heat transfer enhancement in MOSFET mounted on different FR4 substrates by thermal transient measurement?

