Numerical investigation of the time-resolved bubble cluster dynamics by using the interface capturing method of multiphase flow approach*
Ying Chen (陳瑛), Chuan-jing Lu (魯傳敬), Xin Chen (陳鑫), Jie Li (李杰), Zhao-xin Gong (宮兆新)
MOE Key Laboratory of Hydrodynamics, School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China, E-mail: cyofjs@sjtu.edu.cn
Numerical investigation of the time-resolved bubble cluster dynamics by using the interface capturing method of multiphase flow approach*
Ying Chen (陳瑛), Chuan-jing Lu (魯傳敬), Xin Chen (陳鑫), Jie Li (李杰), Zhao-xin Gong (宮兆新)
MOE Key Laboratory of Hydrodynamics, School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China, E-mail: cyofjs@sjtu.edu.cn
2017,29(3):485-494
The present paper proposes a multiphase flow approach for capturing the time-resolved collapse course of bubble clusters in various geometrical configurations. The simulation method is first verified by computing the dynamic behavior of an isolated vapor bubble placed in a uniform ambient pressure. The comparison between the numerical result and the theoretical solution indicates that the method can accurately capture the bubble shape, the characteristic time and the extremely high pressure induced by the collapse. Then the simulation method is applied to investigate the behavior of two kinds of bubble clusters in hexagonal and cubic geometrical configurations. The predicted collapsing sequence and the shape characteristics of the bubbles are generally in agreement with the experimental results. The bubbles transform and break from the outer layer toward the inner layers. In each layer, the bubbles on the corner first change into a pea shape and cave before collapsing, then the bubbles on the sides begin to shrink. It is also found that, in comparison with the case of an isolated single bubble, the central bubble in the cluster always contracts more slowly at the early stage and collapses more violently at the final stage.
Bubble cluster, collapse, numerical simulation, cavitation model
Introduction
Cavitation often occurs in a wide range of hydraulic devices when the static pressure in the fluids drops greatly due to the local high speed. The cavitation erosion effect is caused by the cyclic impact loads of the bubble cluster collapse acting on the tiny area of the solid surface in a very short time. The cavitation erosion was extensively studied, especially, experimentally. It has been a common sense that the internal structure of the bubble cluster inside the cavitation cloud and its collapse process should be more precisely studied, if one intends to go further in the erosion mechanism research. However, the microscopic scale of the bubbles makes experimental techniques impractical in studying the interaction between the bubbles in the course of collapse.
In these days, numerical approaches are playing akey role in the bubble cluster dynamics investigation. A great deal of numerical studies of the bubble evolution were based on solving the Rayleigh-Plesset equation or its modified forms[1,2]. In the cavitating flows, the local vapor fraction often exceeds the dilute limit and the Rayleigh-Plesset equation does not hold true. Therefore the bubble-bubble interaction is an important effect in the bubble flows, as shown by the studies of Seo et al.[3]. Also, some studies concentrated on how the collapse of the neighboring bubbles is affected by their conjunct interaction[4]. Nevertheless, the bubble dynamics equations alone are not enough to well resolve the interaction between the bubbles.
The boundary element method (BEM) based on the inviscid fluid model was widely used for the computation of the bubble dynamics and the bubble-boundary interaction in axisymmetric cases[5-7]and in full 3-D geometric configurations[8,9]. In the multiphase flow framework, the mixture models based on the macroscopic conservation laws coupled with simplified bubble equations were used to simulate the bubble cluster behavior[10]. The most essential issue for such methods is the technique of capturing the bubble surfaces, such as with the VOF method, the level-set method, and the front-tracking method. They were usedto study dilute bubbly flows and were shown to be capable of resolving the flow features. The radial dynamics of the bubbles in compressible fluids were also studied extensively[11-14], where the main focus is on the final stage of the collapse. Recently, Zhang et al.[15]developed a complete model for studying the mutual interaction between cavitation bubbles with the effects of liquid compressibility fully included.
In this paper, the multiphase flow approach based on the homogeneous cavitation model is used to capture the collapse course of the bubble clusters in various geometrical configurations. The primary objective is to investigate the dynamic behavior of the bubble clusters during their collapse and the interaction between the bubbles.
1. Multiphase flow approach
1.1 Volume fraction function
In the traditional bubble dynamics approach, the differential equation for the bubble size or even its spatial distribution function is directly solved, the results obtained are not field-resolved and the bubble surface is regarded as a discontinuous interface. In real flows, the finite distance between the bubbles and the non-symmetric environment invalidate the basis upon which the bubble dynamics equation is founded. Furthermore, the deformation of the bubbles is hard to be taken into account in the traditional way.
This shortcoming can be overcome by using the multiphase flow approach. The transient location and shape of each bubble surface in the cluster are interpolated from the vapor’s volume fraction function,a(r, t ), which denotes the local proportion of the vapor phase inside the liquid/vapor mixture at the coordinatesrand at any given instant t. The distribution of a(r, t) in the 3-D domain is directly resolved and can be written as:

where a0? (0,1) is a selected value which determines the geometry of the bubble surfaces.
In another way, the discrete bubble surface G encircling any vaporous region can be instantaneously constructed from the continuous distribution of a(r, t):


where0a is not required to be explicitly specified.
Equation (2) reveals the fact that the gradient ofa(r, t) across the bubble surface always vertically points out. Numerous contour lines of a can be determined in this way. Using Eq.(3) we can select the most reasonable contour line from those described by Eq.(2). This is because that the change rate of ?a /?n along the radial direction of any bubble reaches its inflection point in the middle of the density transitional region around the bubble interface. Therefore a middle surface for the bubble is picked out through Eq.(3). Additionally, the influence of the interaction between the bubbles on the bubble shapes is also directly observed.
1.2 One-fluid homogeneous model
The volume fraction function (,)taris governed by a phase change process suggested by Zwart et al.[16], and is derived from the Rayleigh-Plesset bubble dynamics equation. A transport equation of the volume fraction is solved, where the mass transfer between the liquid and vapor phases is modeled through the evaporation and condensation source terms:
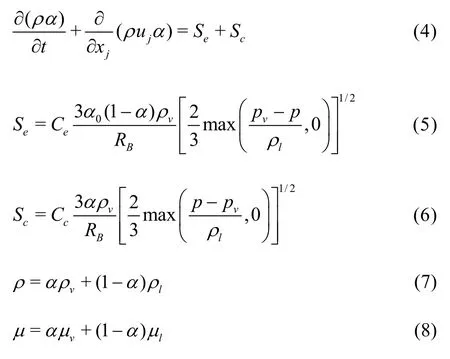
where Ceand Ccare the empirical constants, which are chosen as 50 and 0.01, respectively, a0denotes the initial void fraction of the water due to the dissolved gas nucleus, and RBdenotes the nucleus radius.
With this model, the evolution of the bubble shapes is computed according to the time-dependent dynamic equilibrium between the non-uniform ambient pressure outside any bubble and the vapor pressure inside the bubble. When the local ambient pressure p becomes lower than the vapor pressurevp, the evaporation source described in Eq.(5) works. In this way, theouter liquid close to the bubble may be turned into vapor. The different source intensities distributed along the entire bubble surface produce the 3-D shape of the bubble during its expansion. On the other hand, when the relation p > pvholds, the condensation source in Eq.(6) works and the bubble is changed in the opposite direction.
2. Mathematical model and equations
2.1 Governing equations for bubble cluster simulation
The present study considers the dynamic behavior of the bubbles of initial radius in the millimeter scale. For the collapsing bubbles placed in an initially stationary pressure field, the induced flow is assumed to be entirely in the laminar state, therefore, the turbulence effect is not required to be modeled.
To simulate the evolution of the bubble clusters in any geometrical configuration with the one-fluid homogeneous model, the laminar Navier-Stokes equations are to be solved:

where r and m denote the density and the viscosity of the two-phase mixture, respectively, to be calculated by Eqs. (7) and (8). The gravity effect is neglected because it is one order of magnitude smaller than the pressure and viscous effects, especially, while the bubble radius tends to zero.
Additionally, many experiments indicated that, an extremely high temperature can be produced inside the bubble at the final stage of collapse. Thus the energy conservation is coupled into the model to consider the thermal effect
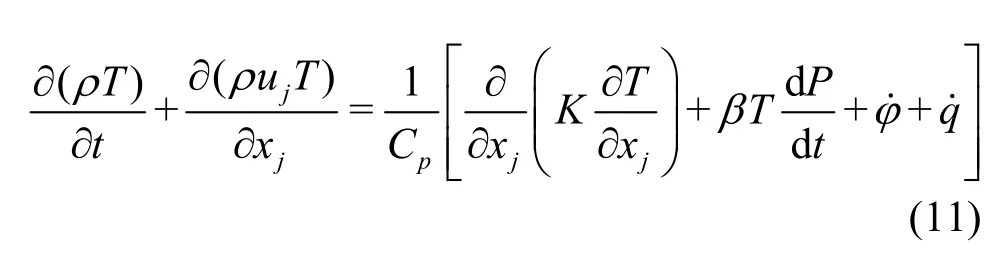
where ? denotes the dissipation term in the energy equation, and b is the thermal expansion coefficient, which is equal to 1/T for an ideal gas.
The specific heat and the thermal conductivity of the mixture are also evaluated as the arithmetic means between the liquid and the vapor values:

The vapor density inside the bubble responds to the local pressure, which may change several orders of magnitude during the bubble evolution. An ideal gas law is employed for the vapor phase. Additionally, to make the pressure-velocity correction algorithm executable, an auxiliary parameter is used to link the density and the pressure, as follows

2.2 Bubble dynamics model and formulation
The bubble dynamics equation was established by Rayleigh and Plesset in the last century for the behavior of an isolated bubble in a uniform ambient pressure

where R denotes the radius of the bubble, p¥denotes the ambient pressure far away from the bubble,0gp denotes the initial partial pressure of the air inside the bubble, and S denotes the surface tension coefficient. In the equation, the effect of the viscosity, the surface tension or the air content inside the bubble can be neglected in different situations to acquire the respective approximate solution.
The change rate of the radius can be obtained by integrating the Rayleigh equation, for which only the pressure term in the right hand side of Eq.(15) is considered. The following is the ultimate normalized expression in the Rayleigh theory:
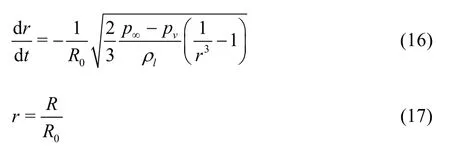
where0R denotes the initial radius of the bubble in equilibrium.
Zhang et al.[17]provided an approximate analytic relation between the radius and the time. If the dimensionless quantityis substituted intoEq.(16), we have

The term (1+ x)-1/6in the above equation is close to unity due to the range x? [0,1]. Thus if this term is replaced by its mean value 0.94, Eq.(18) can be integrated to obtain an explicit expression of the radius

This expression will be used in the following study to verify the numerical simulation result of the collapse of a single bubble.
3. Numerical strategy
The numerical strategy is based on the pressurebased segregated solver developed using the node-centered finite volume method, accelerated by an algebraic multigrid (AMG) method, to solve the governing equations with a fully implicit discretization at any given time step. A SIMPLE-type coupling correction method for arbitrary Mach number is employed, where the correction equation of the pressure contains the convective and unsteady terms, i.e., we have a convected wave equation.
Experiments and mathematical deductions[18-21]both indicate that the speed of sound in the bubbly flow is reduced to several meters per second, much lower than that in single phases. Thus the local Mach number in the entire field will distribute in a wide range. At a low Mach number, the Laplacian term in the correction equation dominates and it is reduced to the Poisson equation. At a high Mach number, the convective term dominates, reflecting the hyperbolic nature of the flow. Thus the coupling correction method automatically adjusts the local nature of the flow and the same method can be applied to the entire flow.
A least squares cell-based evaluation method using the Gram-Schmidt process is used to compute the gradients of the variables appearing in the governing equations.
3.1 Spatial and temporal discretizations
The governing equations in the integral form are used in the finite volume method. To help describe the algorithm, the equation of the scalar f (u, v, w, T and a) on any computational cell with the volume
DV restricted by its faces with the outward area vectorA, can be written in the half-discretized form as

A second order upwind scheme is used to calculate the convection in the momentum equation. The QUICK scheme is used when solving the volume fraction equation describing the evolution of the bubble cluster. These convective terms are treated by using a deferred correction approach, where the convective term is written as the hybrid of an implicit upwind scheme (UDS) and the higher-order convection (HOC) schemes explicitly calculated from the variables obtained in the last iteration. This treatment has advantages in both the computational robustness and the numerical accuracy.
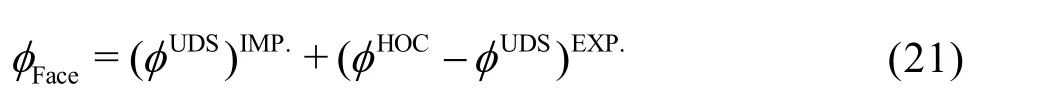
The third-order accuracy will automatically be achieved when the iteration is converged. Some iterative algorithms fail to converge when being applied to the algebraic equation system. This is because the matrix may not be diagonally dominant. In our study, we obtain an algebraic equation having strictly diagonally dominated matrix. The implicit part of the convective term can be split into two parts:
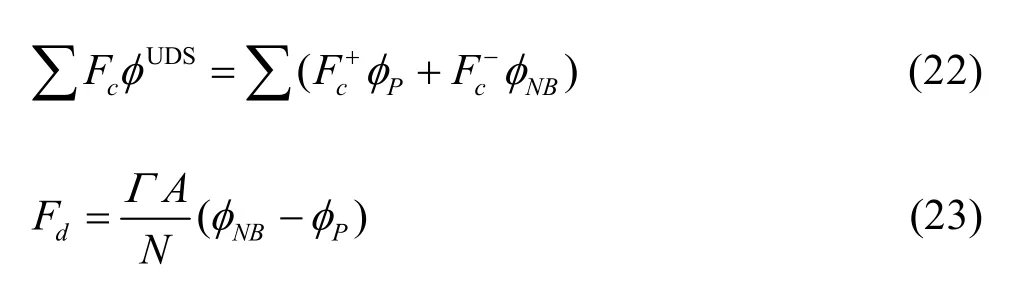
wherecF denotes the mass flux through one of faces on the cell, anddF denotes the diffusive flux. Theanddenote the outward and inward mass fluxes. The continuity equation can be written in a halfdiscretized form as
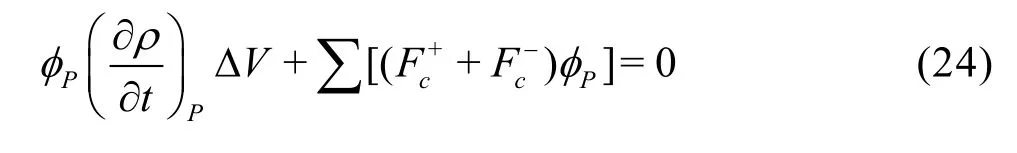
A second order implicit transient formulation is used in the time-dependent computation, to achieve a relatively accurate capture for the bubble collapse. The scheme is discretized as

By substituting these Equations into Eq.(20), the linearized algebraic equation for the variable f is obtained as
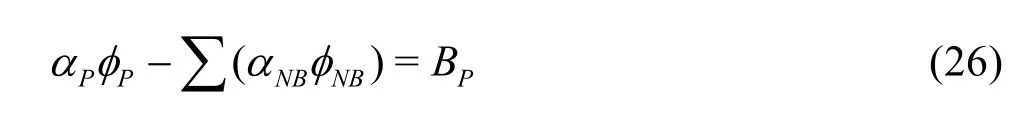
where the coefficient matrix is diagonally dominated as shown below:

3.2 Pressure-velocity-density coupling Algorithm
Two basic computational procedures are adopted at every step within the iteration cycle of the time step t +Dt. First the discretized momentum equation is solved by iteration, as shown below for the iteration step n
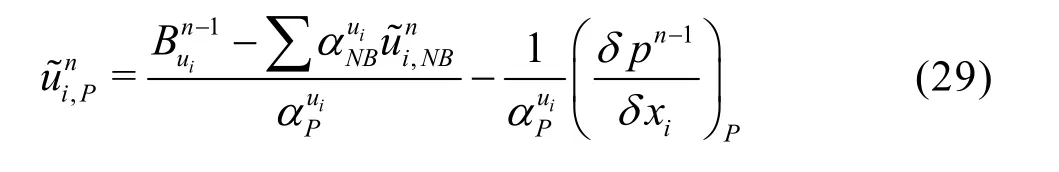
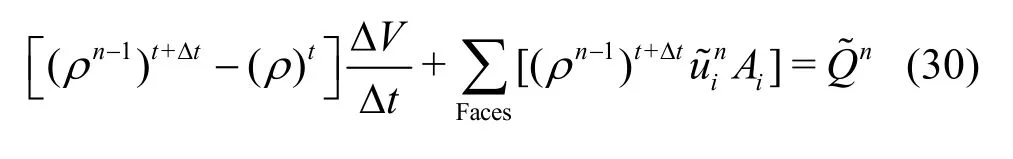
whereiA denotes the normal area vector of the face.
The discretized continuity equation and the corrections for the variables are:
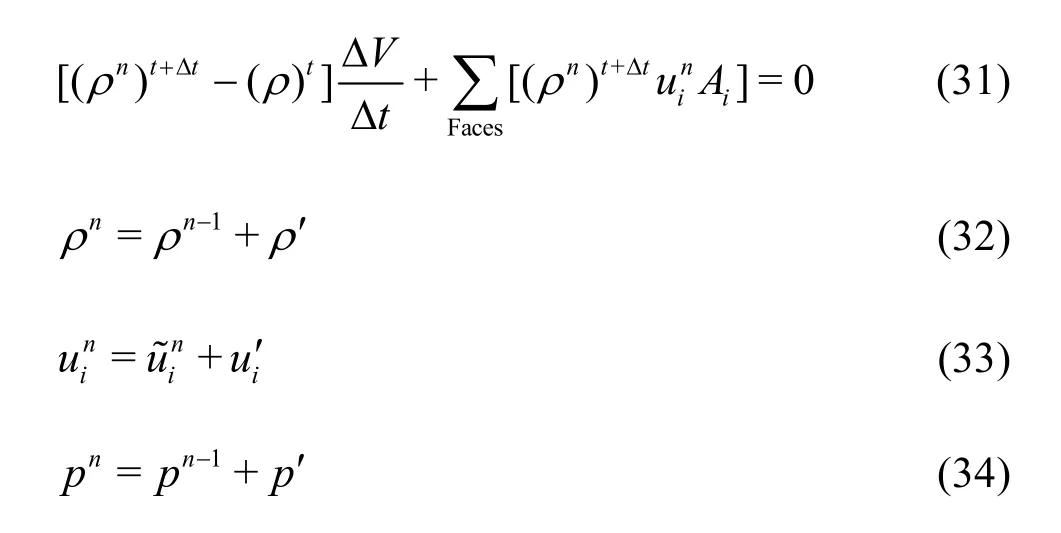
The approximate relations between the corrections for the quantities are


By combining all equations from Eqs.(29) through (36), with the higher order quantities neglected, the final coupling correction equation is obtained as
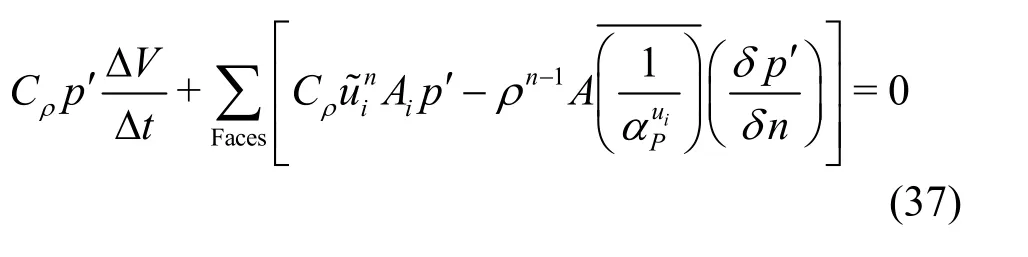
The corrections for the pressure, the velocity and the density can be ultimately computed using this equation and the compressibility relation between r¢and p¢, then the corrections of the velocity and the density can be obtained.
4. Collapse of isolated single bubble
First of all, we have verified the simulation method by computing the dynamic process of an isolated vapor bubble placed in a stationary uniform pressure field. The typical size of the bubble in the cavitating flow is less than 1 mm, and the duration of collapse of the bubble of 1 mm in radius under an external pressure of one bar is about 0.1 ms. We put this bubble in the center of a cubic computational domain with the length of each side being 20 mm.
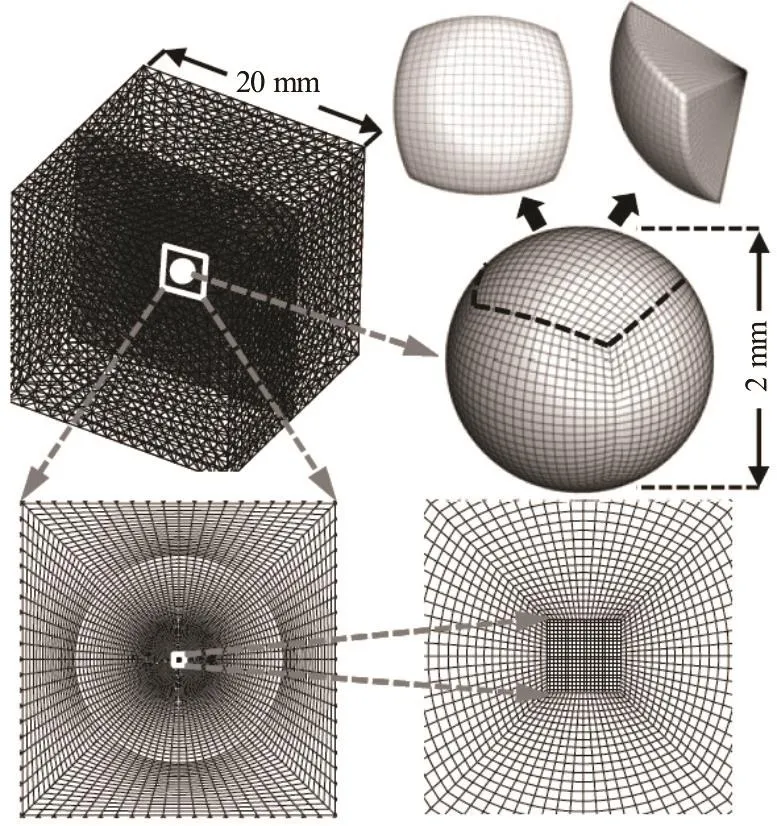
Fig.1 The computational meshes for a single bubble placed in uniform pressure field
The configurations of the computational domain and the meshes are shown in Fig.1. The volume occupied by the initial bubble is cut out in a spherical shape and is divided into six blocks of structured meshes. The center of the sphere is embedded with a micro cube divided into Cartesian meshes with a minimalcell size of 0.5 mm. The rest of the domain is filled with the tetrahedral unstructured meshes. The number of the total computational nodes is 6.8′105.
A zero velocity is initialized in the whole domain, and a uniform pressure of 105Pa is set outside the bubble with an initial pressure pv=3540Pa . A constant pressure p¥=105Pa is specified on the outside boundary of the domain. Since the shrinkage of the bubble keeps accelerating during the collapse, the time step of a variable size is employed from Dt=10-6s at the initial stage to Dt =10-8s at the final stage of the collapse.
The simulated variation process of the bubble shape is shown in Fig.2. The numerical result reflects the primary feature described by the bubble dynamics theory that, the bubble contracts slowly at the early stage and collapses violently to disappear at the final stage. The characteristic time and the time history of the bubble radius are verified quantitatively. The results are shown in Fig.3, in comparison with the theoretical solution and the approximate formula in Eq.(19).
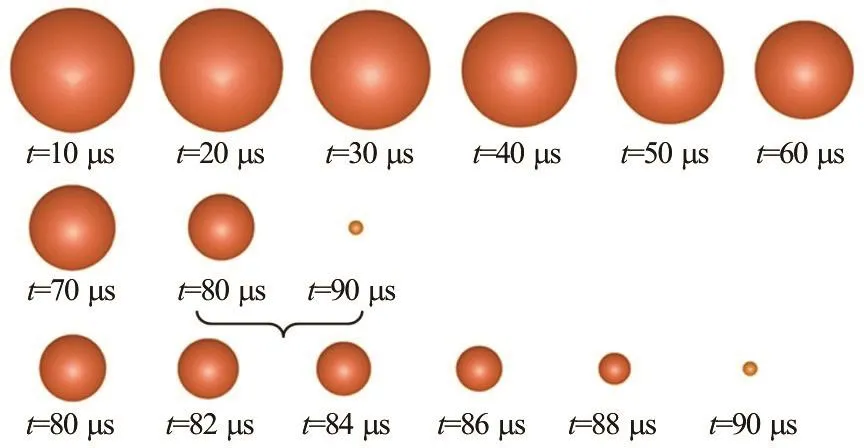
Fig.2 (Color online) A series of snapshots of bubble shapes during the collapse

Fig.3 Time histories of the non-dimensional bubble radius
In this figure the bubble radius is normalized by the initial radius, R0=1mm . It is indicated that there is almost no difference between the results of the Rayleigh-Plesset equation with any effect neglected or not. Also, our numerically predicted radius is acceptable compared with the theoretical ones, especially the acceleration trend in the collapse period and the socalled Rayleigh time which is the total time duration of the collapse. The Rayleigh time obtained in our study is about TR=90 m s , very close to the 91.5 ms predicted by the theory.
According to the bubble dynamics theory with neglect of the fluid viscosity, the distribution of pressure coefficient outside the bubble can be calculated as
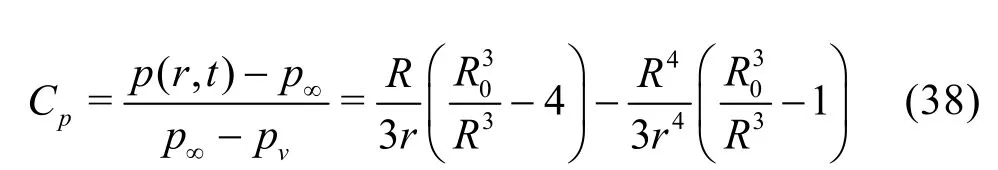
where R denotes the bubble radius at any instant, and r is the local radial coordinate from the center of the bubble.

Fig.4 Comparison between the numerical and analytical pressure distributions outside the bubble at several instants

Fig.5 Capturing of the extremely high pressure around the collapse moment
Figure 4 shows the comparison between the numerically obtained pressure represented by the lines and the analytical ones represented by the symbols. It is indicated that the numerical method can provide a good prediction for the focusing process of the high pressure during the collapse period. The deviation between the parts of the relatively low pressure on the curves is due to the fact that the fluid viscosity is considered in the numerical solution. The curves in Fig.5reflect the fact that the extremely high pressure up to thousands of atmospheric pressure around the collapse moment can be well captured by our numerical simulation.
5. Bubble cluster in planar configuration
Subsequently, we simulate the evolution of a cluster of 37 bubbles placed in a planar hexagon configuration as shown in Fig.6. Bremond et al.[22]produced this multi-bubble system using a negative pressure pulse on a silicon plate with micro-cavities, and investigated the dynamic behavior of this bubble cluster. To compare with their experimental results, the initial size of each bubble in our simulation is0=R 0.0667 mm, and the interval between the centers of two neighboring bubbles is Dr=0.2mm.
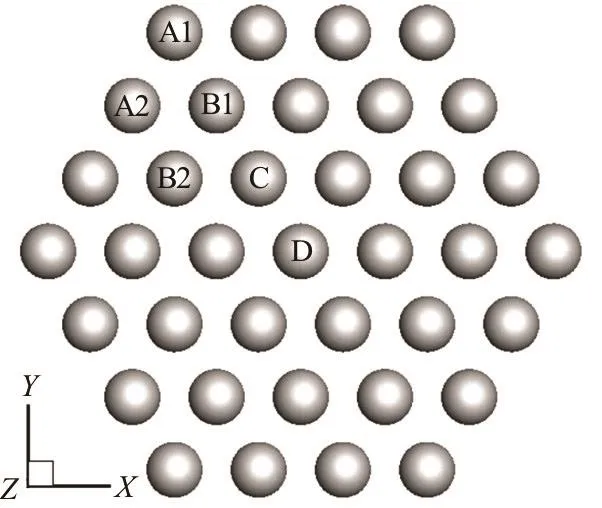
Fig.6 Configuration of the planar bubble cluster composed of 37 bubbles

Fig.7 Computational meshes for the planar bubble cluster
The bubbles shown in Fig.6 can be classified into 6 types according to their respective positions marked by the “A1”, “A2”, “B1”, “B2”, “C”, and “D”. Since the configuration of the bubble cluster is symmetrical about the central bubble, the fluid area is divided and only one eighth of it is adopted as the computational domain, thus three symmetrical boundaries are employed, as shown in Fig.7. The structure of the meshes inside the bubbles is similar to that in the single bubble situation. The space between the bubbles is filled with unstructured meshes with a smooth transition of mesh fineness. The pressure on the outside boundary is also set as p¥=105Pa .

Fig.8 Numerically simulated evolution of the planar hexagonal bubble cluster

Fig.9 Experimental photos of the shapes of the planar hexagon bubble cluster during its collapse

Fig.10 (Color online) A series of snapshots of the course of pressure focusing induced by the collapse of the bubble cluster
The evolution of the bubble cluster is successfully simulated, and the shapes of the bubbles at some typical moments are shown in Fig.8, in comparison to the experimental photos in Fig.9 taken by Bremond et al.[22]. The predicted collapsing sequence and the shape characteristics of the bubbles are generally in agreement with the experimental results. The life period of the bubble cluster is around TR=12 ms , much shorter than 55 ms, the Rayleigh time of a single bubble with a size similar with the bubble cluster, viz.? 0.6mm.
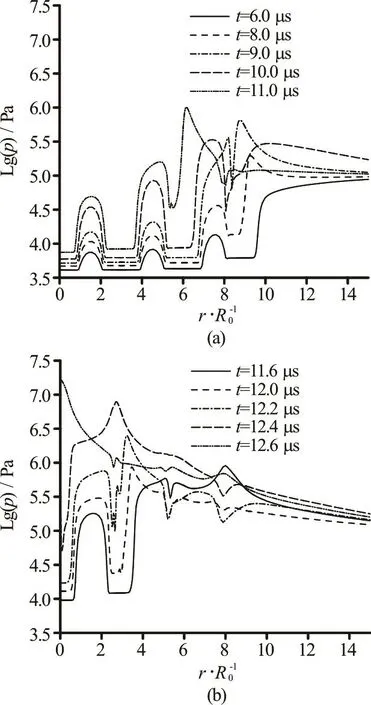
Fig.11 Time-variation of the pressure distribution along the diagonal line of the haxagon through the bubble centers
A primary tendency during the collapse is as follows: the bubbles deforms and breaks from the outer layer “A” toward the inner layers “B”, “C” and“D”. In each of the layers, the bubble on the corner of the hexagon collapses first, as marked by the “A1”and “B1” in Fig.6. Then the bubbles at each side of the hexagon begin to shrink, indicated by the “A2” and “B2”. Each bubble on the outer layer transforms into a pea shape before it collapses completely, but the inner bubbles do not experience such process. The bubble on the center of the cluster contracts along with the evolution of the outer bubble as well, but the contraction is slower than that in the single bubble case. However it collapses more violently after all bubbles outside it have disappeared.
The evolution of the bubble cluster induces the variation of the transient pressure distribution, which conversely affects the behavior of the bubbles until they collapse. The pressure field as well as the bubble shapes at some typical instants are presented in Fig.10. The filled contours in each picture only represent the pressure scope at the corresponding instant, not generally. It is clear that the peak pressure first appears next to the corner bubble around the instant of t =7.5ms. Then the bubbles collapse layer by layer, and the high pressure appears close to the side bubbles and the corner bubbles alternately.

Fig.12 Comparison of the time history of bubble radius for the cases of central bubble in cluster and isolated single bubble
In Fig.11, the pressure distribution along one of the diagonal lines of the bubble cluster is picked out to analyze the time-variation in the course of the collapse. A high pressure peak on the curve is induced around the collapse moment of any bubble. The pressure inside the cluster, especially at the location between twoneighboring bubbles, keep rising as a whole accompanying with the inward moving of the pressure peak.
The speed-up effect of the central bubble collapsing can be clearly seen in Fig.12, as compared with the case of a single bubble. As is verified in Section 4.

Fig.13 Computational meshes for the cubic bubble cluster
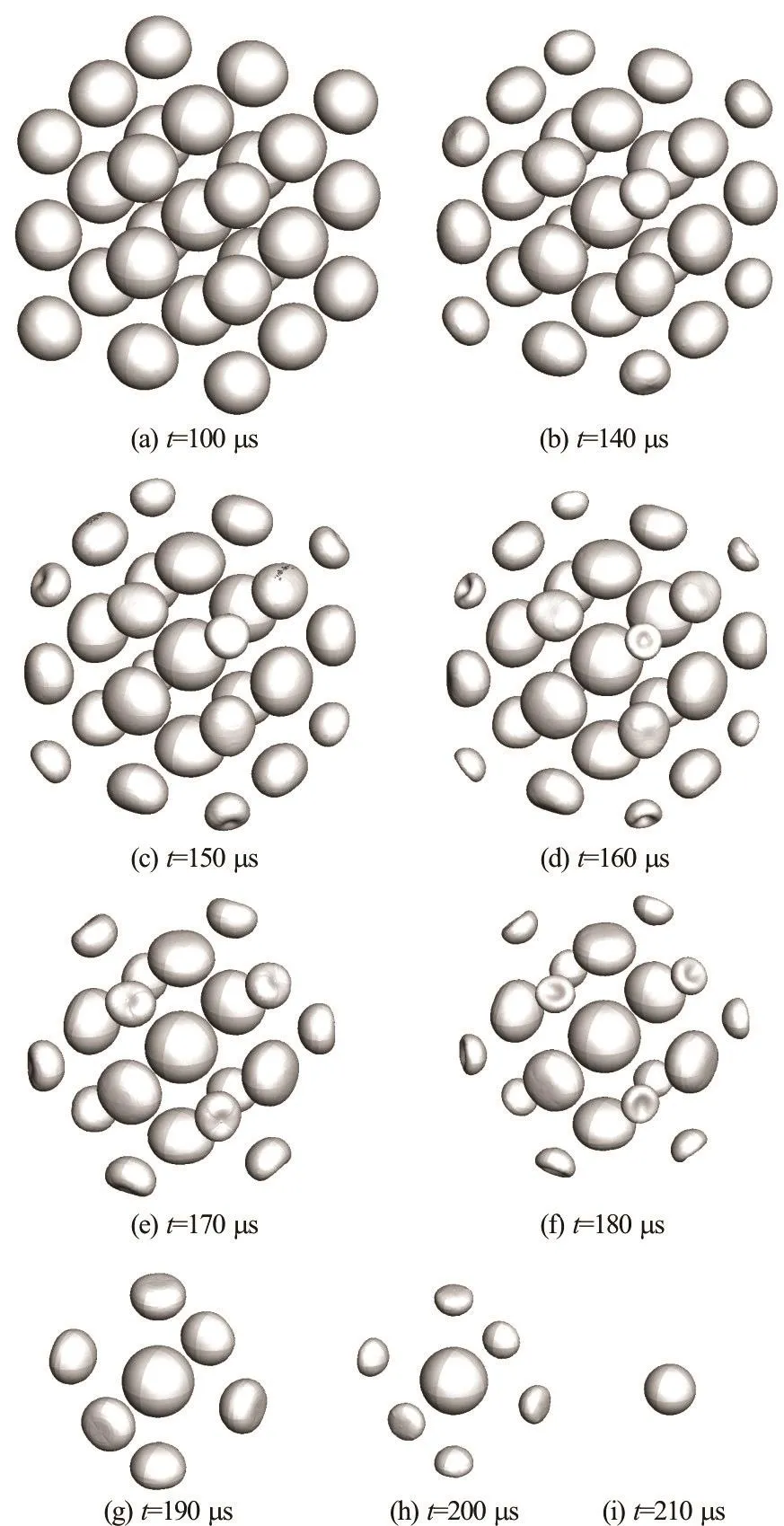
Fig.14 Numerically simulated evolution of the cubic bubble cluster
6. Bubble cluster in cubic configuration
The numerical study is extended to the condition of a cluster of bubbles distributed in a spatial area. We consider the case of 27 bubbles arranged in a cubic shape. Due to the symmetry of the fluid area, we take one eighth of the area as the computational domain, whose meshes are shown in Fig.13.
The simulated evolution of the cubic bubble cluster is shown in Fig.14, where the interaction between the bubbles make each bubble at different positions to transform its shape in order. The bubbles on the corner of the cube are caved greatly along with its shrinkage. Although the bubbles on the side or the face center of the cube also suffer a large pressure outside them, they are just flattened rather than caved inwards.
7. Conclusions
This study adopts a multiphase flow simulation approach based on the homogeneous cavitation model and its corresponding numerical methods to capture the time-resolved collapse process of the bubble clusters in various geometrical configurations.
The simulation method is firstly verified by computing the dynamic behavior of an isolated vapor bubble placed in a stationary uniform pressure field. The comparison between the numerical result and the theoretical solution indicates that the method can provide an accurate capturing for the collapse process, the characteristic time and the extremely high pressure induced by the collapse.
Then the numerical simulation method is applied to investigate the behavior of two kinds of bubble clusters in hexagonal and cubic geometrical configurations. The predicted collapsing sequence and the shape characteristics of the bubbles are generally in agreement with the experimental results. The bubbles transform and break from the outer layer toward the inner ones. In each layer, the bubbles on the corner first change into a pea shape and cave before collapsing, then the bubbles on the sides begin to shrink. It is also found that, in comparison with the case of an isolated single bubble, the central bubble in the cluster always contracts more slowly at the early stage and collapses more violently at the final stage.
[1] Vedadi M. Structure and dynamics of shock-induced nanobubble collapse in water [J]. Physical Review Letter, 2010, 105(1): 014503.
[2] Xu W. L., Bai L. X., Zhang F. X. Interaction of a cavitation bubble and an air bubble with a grid boundary [J]. Journal of Hydrodynamics, 2010, 22(4): 503-512.
[3] Seo J. H., Lele S. K., Tryggvason G. Investigation andmodeling of bubble-bubble interaction effect in homogeneous bubbly flows [J]. Physics of Fluids, 2010, 22(6): 063302.
[4] Brujan E. A., Ikeda T., Yoshinaka K. et al. The final stage of the collapse of a cloud of bubbles close to a rigid boundary [J]. Ultrasonics Sonochemistry, 2011, 18(1): 59-64.
[5] Lind S. J., Phillips T. N. The influence of viscoelasticity on the collapse of cavitation bubbles near a rigid boundary [J]. Theoretical and Computational Fluid Dynamics, 2012, 26(1-4): 245-277.
[6] Curtiss G. A., Leppinen D. M., Wang Q. X. et al. Ultrasonic cavitation near a tissue layer [J]. Journal of Fluid Mechanics, 2013, 730: 245-272.
[7] Wang Q. X. Underwater explosion bubble dynamics in a compressible liquid [J]. Physics of Fluids, 2013, 25(7): 072104.
[8] Jayaprakash A., Hsiao C. T., Chahine G. Numerical and experimental study of the interaction of a spark-generated bubble and a vertical wall [J]. Journal of Fluids Engineering, 2012, 134(3): 031301.
[9] Jayaprakash A., Singh S., Chahine G. Experimental and numerical investigation of single bubble dynamics in a two-phase bubbly medium [J]. Journal of Fluids Engineering, 2011, 133(12): 121305.
[10] Bonhomme R., Magnaudet J., Duval F. et al. Inertial dynamics of air bubbles crossing a horizontal fluid-fluid interface [J]. Journal of Fluid Mechanics, 2012, 707: 405-443.
[11] Wang Q. X., Blake J. R. Non-spherical bubble dynamics in a compressible fluid. Part 1. Travelling acoustic wave [J]. Journal of Fluid Mechanics, 2010, 659: 191-224.
[12] Wang Q. X., Blake J. R. Non-spherical bubble dynamics in a compressible fluid. Part 2. Acoustic standing wave [J]. Journal of Fluid Mechanics, 2011, 679: 559-581.
[13] Yang Y. X., Wang Q. X., Keat T. S. Dynamic features of a laser-induced cavitation bubble near a solid boundary [J]. Ultrasonics Sonochemistry, 2013, 20(4): 1098-1103.
[14] Wang Q. X. Multi-oscillation of a bubble in a compressible liquid near a rigid boundary [J]. Journal of Fluid Mechanics, 2014, 745: 509-536.
[15] Zhang Y. N., Min Q., Du X. Z. Effects of liquid compressibility on bubble-bubble interactions between oscillating bubbles [J]. Journal of Hydrodynamics, 2016, 28(5): 832-839.
[16] Zwart P. J., Gerber A. G., Belamri T. A two-phase flow model for predicting cavitation dynamics [C]. The 5th International Conference on Multiphase Flow. Yokohama, Japan, 2004.
[17] Zhang L. X., Yin Q., Shao X. M. Theoretical and numerical studies on the bubble collapse in water [J]. Chinese Journal of Hydrodynamics, 2012, 27(1): 68-73(in chinese).
[18] Shin B. R., Iwata Y., Ikohagi T. Numerical simulation of unsteady cavitating flows using a homogeneous equilibrium model [J]. Computational Mechanics, 2003, 30(5-6): 388-395.
[19] Saito Y., Takami R., Nakamori I. et al. Numerical analysis of unsteady behavior of cloud cavitation around a NACA0015 foil [J]. Computational Mechanics, 2007, 40(1): 85-96.
[20] Chen Y., Lu C. J., Chen X. et al. Numerical investigation on the cavitation collapse regime around the submerged vehicles navigating with deceleration [J]. European Journal of Mechanics B/Fluids, 2015, 49: 153-170.
[21] Chen Y., Chen X., Li J. et al. Large eddy simulation and investigation on the flow structure of the cascading cavitation shedding regime around 3D twisted hydrofoil [J]. Ocean Engineering, 2017, 129: 1-19.
[22] Bremond N., Arora M., Ohl C. et al. Controlled multibubble surface cavitation [J]. Physical Review Letters, 2006, 96(22): 224501.
10.1016/S1001-6058(16)60760-6
October 6, 2015, Revised January 7, 2016)
* Project supported by the National Natural Science Foundation of China (Grant Nos. 11472174, 11572194 and 11372185).
Biography:Ying Chen (1979-), Male, Ph. D.,
Associate Professor
 水動(dòng)力學(xué)研究與進(jìn)展 B輯2017年3期
水動(dòng)力學(xué)研究與進(jìn)展 B輯2017年3期
- 水動(dòng)力學(xué)研究與進(jìn)展 B輯的其它文章
- Standing wave at dropshaft inlets*
- Shedding frequency of sheet cavitation around axisymmetric body at small angles of attack*
- Numerical analysis of bubble dynamics in the diffuser of a jet pump under variable ambient pressure*
- Shock waves and water wing in slit-type energy dissipaters*
- Optimal contract wall for desired orientation of fibers and its effect on flow behavior*
- The influence of nonlinear shear stress on partially averaged Navier-Stokes (PANS) method*
