Comparison of two projection methods for modeling incompressible flows in MPM*

Shyamini Kularathna, Kenichi Soga

1. Department of Engineering, Geotechnical and Environmental Research Group, University of Cambridge, Cambridge, UK, E-mail:srhgk2@cam.ac.uk

2. Department of Civil and Environmental Engineering, University of California Berkeley, Berkeley, USA

Comparison of two projection methods for modeling incompressible flows in MPM*

Shyamini Kularathna1, Kenichi Soga2

1. Department of Engineering, Geotechnical and Environmental Research Group, University of Cambridge, Cambridge, UK, E-mail:srhgk2@cam.ac.uk

2. Department of Civil and Environmental Engineering, University of California Berkeley, Berkeley, USA

2017,29(3):405-412

Material point method (MPM) was originally introduced for large deformation problems in solid mechanics applications. Later, it has been successfully applied to solve a wide range of material behaviors. However, previous research has indicated that MPM exhibits numerical instabilities when resolving incompressible flow problems. We study Chorin’s projection method in MPM algorithm to simulate material incompressibility. Two projection-type schemes, non-incremental projection and incremental projection, are investigated for their accuracy and stability within MPM. Numerical examples show that the non-incremental projection scheme provides stable results in single phase MPM framework. Further, it avoids artificial pressure oscillations and small time steps that are present in the explicit MPM approach.

Chorin’s projection method, material point method (MPM), incompressible flow, time step

Introduction

Traditionally, material point method (MPM) is implemented using a dynamic explicit formulation. The presence of numerical instabilities in the explicit MPM implementations of incompressible problems have been highlighted in a number of previous studies.

In incompressible fluid mechanics applications, the explicit time integration in the standard MPM leads to a weakly compressible formulation. The pressure field is approximated using an equation of state (EOS) which relates pressure to the volume change of the flow. This artificial relationship causes pressure oscillations for small fluctuations in the volume change at near incompressible conditions.

This weakly compressible MPM with strain enhancement techniques and pressure smoothing is capable of avoiding severe numerical issues such as volume locking. However, it requires a significantly small time step to minimize numerical instabilities. An implicit formulation appears to be a suitable solution to the problem of small time steps. However, implementing non-linear problems and incompressibility in the implicit MPM is not trivial. Most importantly, the computational cost of the implicit formulation is not desirable in most practical applications such as problems involving history dependent materials and large deformations.

On the other hand, MPM can be augmented with an operator splitting technique as can be seen in many fluid mechanics applications. Chorin-style projection method which was first introduced in the ground breaking study[1]is the most employed splitting method in the literature. Projection methods have also been successfully used in finite element modeling of viscous incompressible materials[2-4].

Projection-type splitting of governing equations is first applied within MPM in a recent work[5]. They demonstrate that this novel MPM formulation can handle a wide variety of material behaviors. Using a marker and cell (MAC) grid based MPM solver, this study[5]successfully solves phase transition and heat transfer problems such as melting and solidifying. We presented a similar splitting of incompressible governing equations in Ref.[6]. A recent study[7]also employs a projection type splitting algorithm in MPM for modeling free surface fluid flow problems. In their study, finite difference approach with asemi-staggered grid is used to spatially discretise the governing equations forincompressible fluid.

The MPM formulation presented in this paper and the original work in Ref.[6] mainly differs from studies[5,7]by the spatial discretization. Furthermore, this paper investigates two different projection schemes for their stability and accuracy within the single phase MPM framework using a linear structured mesh. Therefore, this study makes an important contribution to the field of incompressible MPM by investigating the applicability of popular projection-type schemes in MPM.

The first section of this paper presents the governing equations for incompressible flow followed by the projection-type splitting of governing equations. The formulation of MPM based on these two projection methods is presented in the next section. Numerical examples which show the accuracy of the two methods within MPM framework are presented. Finally, the conclusion gives a brief summary and critique of the findings.

1. Formulation of single phase MPM based on projection method

This section presents the formulation of MPM based on the projection method. Two projection-type schemes, non-incremental projection and incremental projection, are investigated for their accuracy within MPM. An overview of different schemes of projection method and their strengths/limitations are presented in Ref.[8].

1.1 Governing equations and incompressibility constraint

The motion of a continuum body (?)is governed by the balance equations for mass, Eq.(1) and momentum Eq.(2).

with Dirichlet boundary condition as

whereρis the density,vis the velocity,σis the Cauchy stress tensor andbis the body force.

A constitutive relationship between stressσand deformation which is specific to the material completes the governing equations of the physical problem. In order to employ the projection method, it is necessary to split the Cauchy stress tensorσinto a dilational partp and a deviatoric partτas

whereΙis the identity matrix.

In the case of incompressible flow which is essentially a volume preserving motion of materials, the kinematic requirement is a divergence free velocity field as

1.2 Time discretisation and splitting of governing equations

A fully implicit time integration scheme results in a coupled set of equations for the velocity and pressure fields. However, a semi-implicit time integration scheme is employed in this study in order to preserve the MPM approach of solving constitutive equations at material points.

The time discretised governing equations are

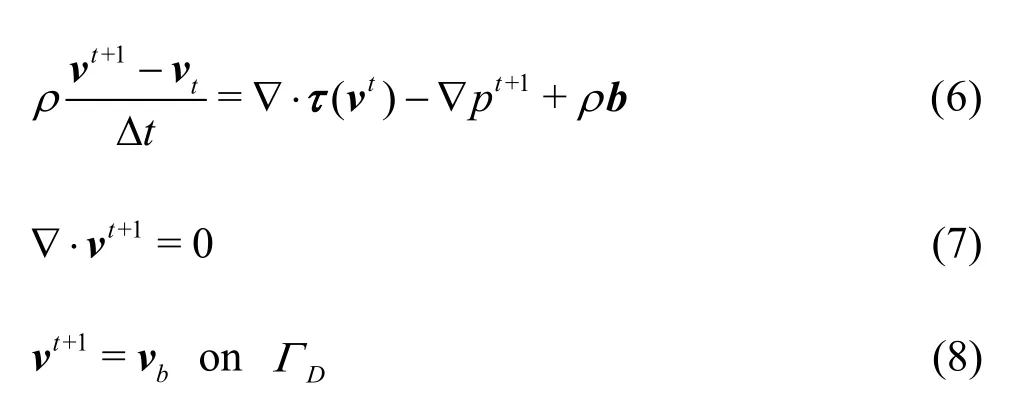
Solving velocity,vt+1and pressure,pt+1using the coupled Eqs.(6) and (7) is a tedious process. Hence, in 1968, Chorin[1]first introduced splitting the equations using an intermediate velocity field,v?. This solution scheme is well known as the projection method. Later, different classes of projection-type solution scheme were investigated in order to obtain a higher order of accuracy for the incompressible problem.

This study aims to investigate the performance of two different projection-type solution schemes, nonincremental projection and incremental projection, within MPM. In both methods, the equation of motion (6) is split into two sub steps. The two variations use the pressure term in the first sub step in different ways as shown in the following sections.

In the non-incremental projection method, the pressure is omitted from the first sub step. Splitting Eq.(6) gives

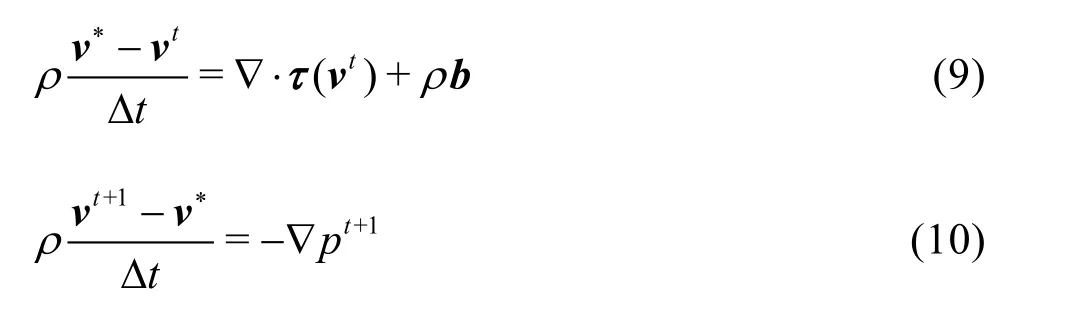
Taking the divergence of Eq.(10) and substituting Eq.(7) for ??vt+1yields

Incremental projection method treats the pressure term explicitly in the first sub step as

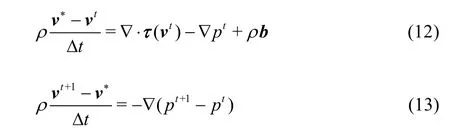
Similarly, taking the divergence of Eq.(13) and substituting Eq.(7) for ??vt+1gives a Poisson-like equation for the pressure as

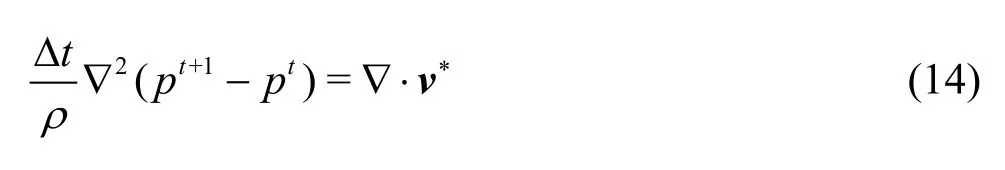
A unified set of Eqs.(15)-(17) for the two projection-type methods is used in the following sections for the simplicity of presentation.

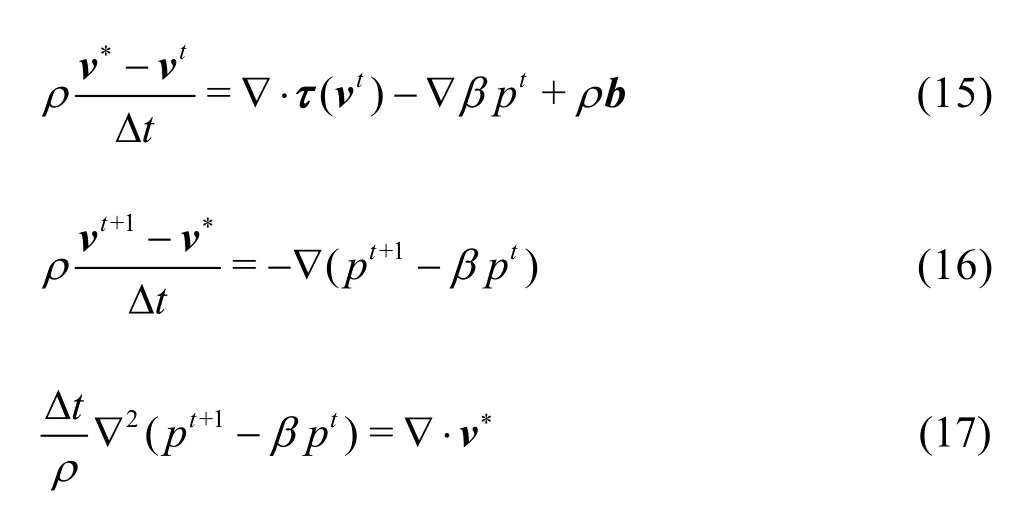
where β=0for non-incremental solution scheme and β=1for incremental projection type.

1.3 Weak formulation and spatial discretisation

MPM describes the whole material domain?with a set of Lagrangian material points npthat are tracked throughout the deformation process. A Eulerian grid is used to solve the equation of motion. The background mesh consists of a total number of nodes,nnthat are located at xiwith shape functions Ni(x) (i =1,2,L ,nn). A mixed integration scheme as described in Ref.[6] is used to avoid poorly constructed matrices resulting from randomly positioned material points. This approach basically applies Gauss integration for the elements filled with particles and material points based integration for the elements partially filled with particles.

The matrix forms of the fully discretised equations can be written as

where Mijis the consistent mass matrix defined by

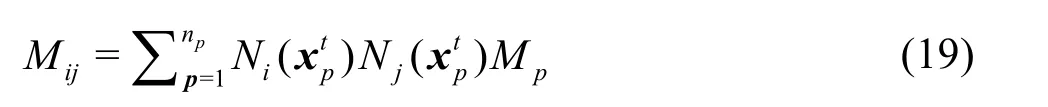
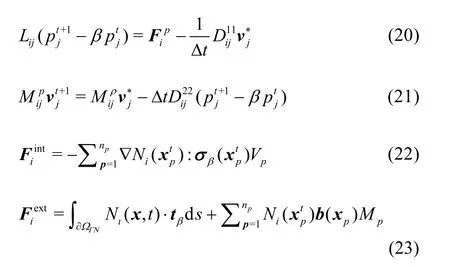
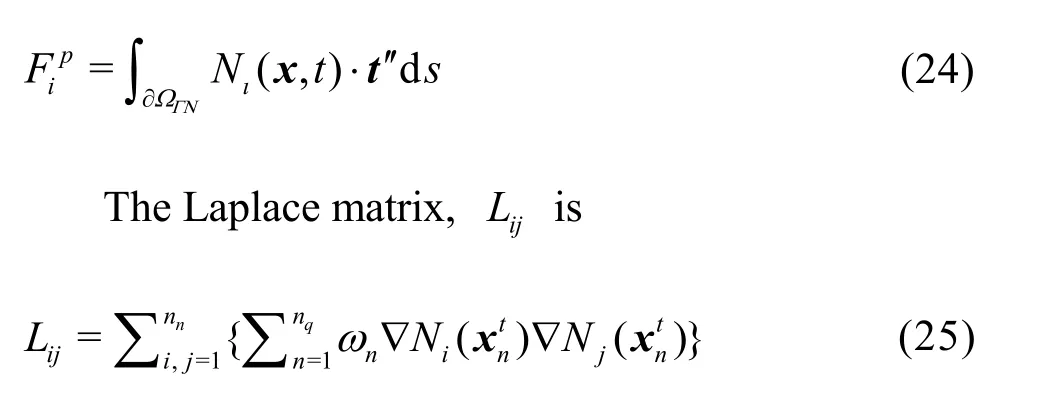
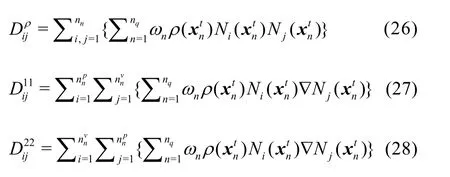
In these equations,is the total/deviatoric stress tensor depending on the scalar value ofβ,?nis the surface traction force andt′=? (pt+1? βpt)?nis an artificial pressure boundary force.nis the normal vector to the boundary/?t is an intermediate acceleration field,nqis the number of integration points which can be either material particles or Gauss points,andnare respectively pressure and velocity degrees of freedom.

2. MPM implementation of projection method

The numerical implementation of the projection-MPM formulation at each Lagrangian time step consists of three main sub-steps as:

(1) Solve intermediate velocity field,v?using Eq.(18).

(2) Solve pressure Eq.(20).

(3) Correct the intermediate velocity using Eq.(21).

2.1 Computation of the intermediate velocity field

Equation (18) for the intermediate velocity field in projection-MPM is equivalent to the discretised equation of motion in the standard explicit MPM formulation with a different interpretation for the acceleration. Therefore, Eq.(18) is solved by replacing the consistent mass matrix with a diagonal lumped mass matrix. This gives

The intermediate velocity at nodes is then calculated by

In order to solve Eqs.(29) and (30), the mass,mpand the velocity,of material particles are extrapolated to the background grid nodes as

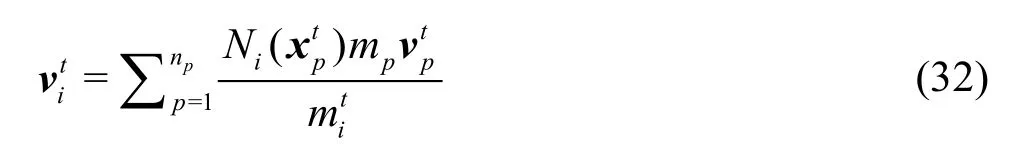
2.2 Pressure calculation

The symmetric positive definite matrix Eq.(19) is then solved in order to obtain the pressure,pt+1. With zero homogeneous Neumann pressure boundary condition as described in Ref.[6], the pressure Poisson Eq.(19) is solved as

where

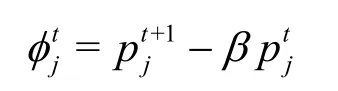
The non-incremental Chorin’s projection method can be deduced from Eq.(33) for β=0which gives

For the incremental projection method (i.e., for β=1), the pressure,is updated at nodes using

2.3 Velocity update

The final sub step is to solve Eq.(20) which gives the final velocity field,vt+1. Note that the consistent mass matrix is used in this computational step contrary to the lumped mass matrix which is commonly seen in MPM. Then, the nodal acceleration at timetis computed as

2.4 Particle update

At the end of each Lagrangian time step, the material particles are updated using the nodal values. The velocity of the material points is updated as

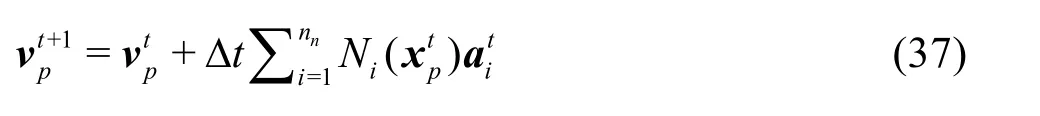
and the particle positions are updated using

Finally, the pressure at the material points is updated as

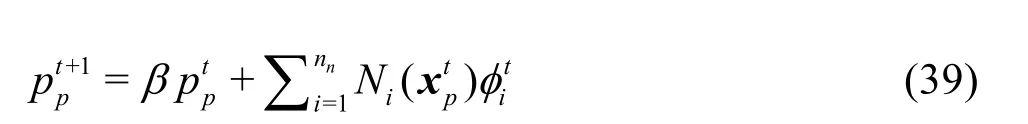
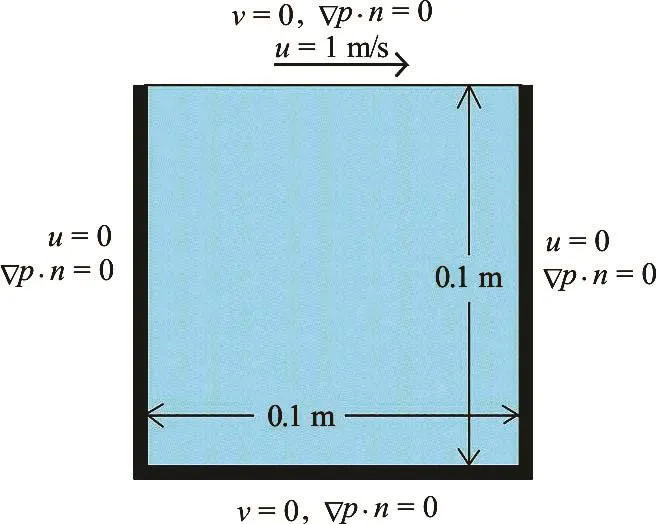
Fig.1 (Color online) Geometry and boundary conditions for shear driven cavity problem

3. Numerical examples

3.1 Shear driven lid driven cavity problem

Traditionally, shear driven cavity has served as a model problem for validating numerical methods in fluid dynamics. In this problem, a laminar incompressible flow is driven by the top lid which is moving at uniform velocity inx-direction (see Fig.1).

The Reynolds number(R e)as defined by Eq.(40) governs the flow characteristics such as eddies and vortices inside the cavity. ForRe=1, the flow is almost symmetric with respect to the center vertical line of the cavity. As Re increases, the main vortex moves towards the downstream of the cavity and eddies are formed at corners. Numerical results are presented for a wide range of values of Re in many studies[9-12].

wherev is the fluid velocity,dis the length of the flow andμis the dynamic viscosity of the fluid.

Since the material particles in MPM move with the velocity field, the corner eddies present in the lid driven cavity create numerical instabilities. This can be solved by splitting the particles which are located at eddies. Particle splitting algorithm is not considered in this study. However, this can be considered for more important practical problems in future studies.

Without a particle splitting algorithm or an alternative technique in MPM, the shear driven cavity problem cannot be modeled for high Reynolds number. Therefore, in MPM analysis, the positions of particles were not updated during the computation. More importantly, the problem was analysed only for Re=10 with nearly symmetric flow. Using this simplified approach, the accuracy and the stability of the two projection methods in MPM algorithm for incompressible materials are investigated.

The problem was analysed using the two projection methods:β=0for non-incremental approach andβ=1for incremental approach. The cavity was divided into a 20×20 quadrilateral (2-D) mesh. 16 particles per cell (PPC) were used to represen3t water. The density of water was taken as 1 000 kg/m. Newtonian model was assumed for water with dynamic viscosity (μ)taken as 10 Pa?s. The problem was analysed for 0.5 s with time step size of 0.001 s.

Figure 2 shows the pressure distribution at the end of MPM analysis using the two projection schemes. The incremental projection method was unable to produce a smooth pressure field. On the other hand, the non-incremental projection scheme successfully resolved the pressure field without artificial oscillations. The velocity distribution as shown in Figs.3 and 4 also follows the same patterns of pressure variation.

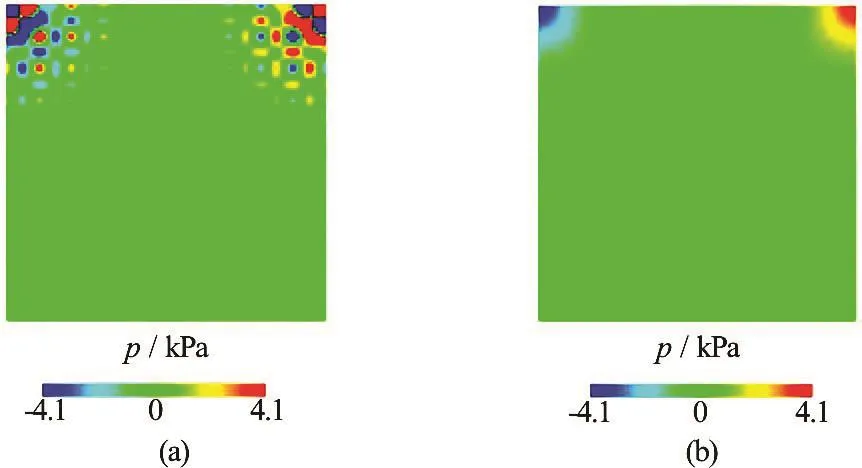
Fig.2 (Color online) MPM pressure distribution for shear driven cavity problem for Re=10

Fig.3 (Color online) MPM velocity distribution in x-direction for shear driven cavity problem forRe=10

Fig.4 (Color online) MPM velocity distribution in y-direction for shear driven cavity problem forRe=10

The poor performance of the incremental projection method is related to the equal order interpolation functions for velocity and pressure employed in the MPM algorithm. Generally, the projection method is considered as stable for the finite elements that are not compatible with the inf-sup condition. However, the incremental projection method provides unstable results for equal order elements. On the other hand, the non-incremental projection method exhibits intrinsic pressure stability. This difference of the stability between the two projection methods is also illustrated in Ref.[13].

3.2 Dam break problem

In this numerical example, the collapse of a rectangular water column is analysed. The initial configuration of the problem is shown in Fig.5. The water column with height,H and length,Lis initially supported by a gate which is removed at the beginning of the test. This problem is commonly adopted in many studies as a benchmark test to investigate the performance of numerical methods in free surface flow applications[14-16].

The MPM simulations of dam break problem in this study was carried out according to the experimental work presented by Ref.[16] as shown in Fig.5(a). The 2-D MPM model with boundary conditions is shown in Fig.5(b). A water column of aspect ratio, Ar=2was considered. A 37×39 quadrilateral mesh was used. The water column was represented by 16 particles per cell. The Newtonian fluid properties are: density,ρ=1000kg/m3and dynamic viscosity, μ=0.001Pa?s. The analysis was carried out for 1.0 s with a time step size of 0.001 s.

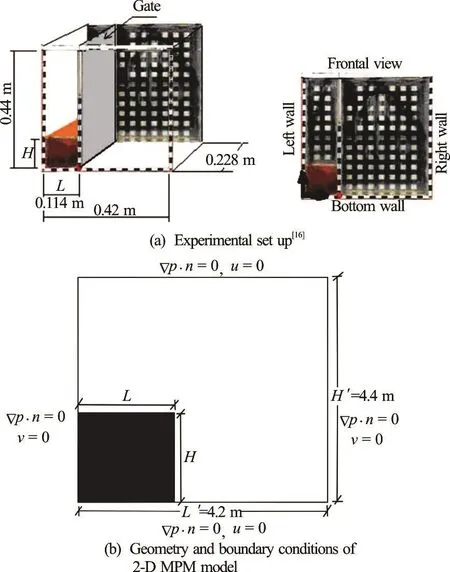
Fig.5 (Color online) Dam break problem

The incremental projection method was unable to provide stable results for the dam break problem. It suffered from severe numerical instabilities when material particles started to cross grid elements. It was observed that a high particle density such as 100 PPC avoids some of the instabilities. However, the incremental projection method failed to successfully model the complex flow characteristics of the water column.

On the other hand, the non-incremental projection method successfully analysed the flow of water column. As shown in Fig.6, the experimental results for 0.1 s-0.5 s are successfully approximated by the nonincremental projection method in MPM. The slight deviation of the numerical results from the experimental data from 0.6 s to 1.0 s is due to the coarse mesh. The isolated particles (see Figs.6(f)-6(j)) in the MPM analysis are produced as a result of grid crossing error and the free surface algorithm. As the flow evolves in time, a number of elements has a low particle density. The free surface capturing algorithm adopted in the formulation identifies these elements and assigns the free surface condition. Consequently, these elements have a zero pressure gradient and therefore, the velocity field is not resolved accurately. This issue can be avoided using a fine mesh. Alternatively, the volume of fluid method coupled with a level set method can produce a more accurate interface.

Overall, there is a close agreement between the numerical and experimental results for the dam break problem. Further, the non-incremental projection MPM method provides a satisfactory pressure distribution throughout the computation (see Fig.6).

4. Conclusions

This paper investigates the accuracy and stability of two projection type solution schemes within MPM framework for modeling incompressible materials. The numerical results show that the incremental projection method exhibits numerical instabilities for equal order finite elements while the non-incremental projection method successfully resolves incompressible flow problems. The key strengths of the present MPM formulation are large time steps compared to significantly small time steps in explicit formulations, less numerical instabilities in incompressible flow conditions and the ability to use a linear structured mesh. The findings of this study provide additional evidence to the work[6]and together, this work makes several note worthy contributions to incompressible MPM applications.

The present MPM algorithm can be further improved with a more accurate interface capturing method. This will avoid isolated particles in MPM simulations of free surface problems. More importantly, the current study has only examined fluid mechanics applications. It would be interesting to assess the performance of MPM with projection method inproblems with complex material behaviors.

Acknowledgements

This study has been financially supported by the Cambridge Commonwealth Trust and the European Union’s Seventh Framework Programme 662 for research, Technological Development and Demonstration under Grant Agreement No. PIAP-GA-663 2012-324522 (MPM Dredge).

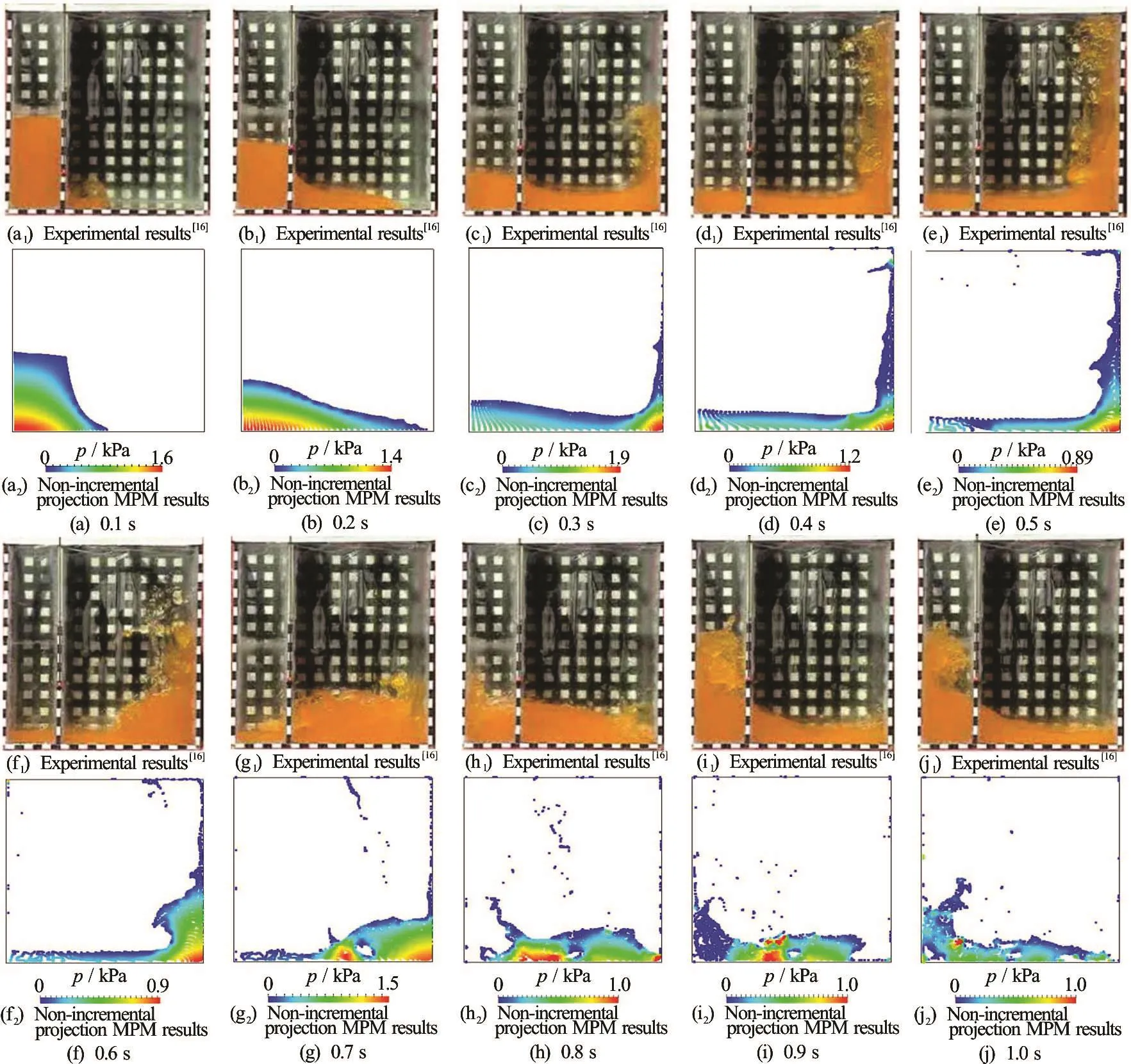
Fig.6 (Color online) Dam break problem with a water column of aspect ratio,Ar=2

[1] Chorin A. J. Numerical solution of the navier-stokes equations [J]. Mathematics of Computation, 1968, 22(104): 745-762.

[2] Schneider G., Raithby G., Yovanovich M. Finite element solution procedures for solving the incompressible, Navier-Stokes equations using equal order variable interpolation [J]. Numerical Heat Transfer, 1978, 1(4): 433-451.

[3] Kawahara M., Ohmiya K. Finite element analysis of density flow using the velocity correction method [J]. International Journal for Numerical Methods In Fluids, 1985, 5(11): 981-993.

[4] Guermond J., Quartapelle L. Calculation of incompressible viscous flows by an unconditionally stable projection fem [J]. Journal of Computational Physics, 1997, 132(1): 12-33.

[5] Stomakhin A., Schroeder C., Jiang C. et al. Augmented MPM for phase-change and varied materials [J]. ACM Transactions on Graphics, 2014, 33(4): 1-11.

[6] Kularathna S., Soga K. Implicit formulation of material point method for analysis of incompressible materials [J]. Computer Methods in Applied Mechanics and Engineering, 2017, 313(1): 673-686.

[7] Zhang F., Zhang X., Lian Y. P. et al. Incompressible material point method for free surface flow [J]. Journal of Computational Physics, 2017, 330: 92-110.

[8] Guermond J., Minev P., Shen J. An overview of projection methods for incompressible flows [J]. Journal of Computational Physics, 2006, 195(44-47): 6011-6045.

[9] Ghia U., Ghia K., Shin C. High-re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method [J]. Journal of Computational Physics, 1982, 48(3): 387-411.

[10] Schreiber R., Keller H. Driven cavity flows by efficient numrical techniques [J]. Journal of Computational Physics, 1983, 49(2): 310-333.

[11] Kim J., Moin P. Application of a fractional-step method to incompressible Navier-Stokes equations [J]. Journal of Computational Physics, 1985, 59(2): 308-323.

[12] Sousa R. G., Poole R. J., Afonso A. M. et al. Lid-driven cavity flow of viscoelastic liquids [J]. Journal of Non-Newtonian Fluid Mechanics, 2016, 234: 129-138.

[13] Guermond J.-L., Quartapelle L. On stability and convergence of projection methods based on pressure Poisson equation [J]. International Journal For Numerical Metho-ds in Fluids, 2015, 26(9): 1039-1053.

[14] Lee E. S., Moulinec C., Xu R. et al. Comparisons of weakly compressible and truly incompressible algorithms for the SPH mesh free particle method [J]. Journal of Computational Physics, 2008, 227(18): 8417-8436.

[15] Liu M. B., Xie W. P., Liu G. R. Modeling incompressible flows using a finite particle method [J]. Applied Mathematical Modeling, 2005, 29(12): 1252-1270.

[16] Cruchaga M. A., Celentano D. J., Tezduyar T. E. Collapse of a liquid column: Numerical simulation and experimental validation [J]. Computational Mechanics, 2006, 39(4): 453-476.

10.1016/S1001-6058(16)60750-3

February 13, 2017, Revised March 18, 2017)

*Biography:Shyamini Kularathna, Female, Ph. D. Candidate