ON GENERALIZED FEYNMAN-KAC TRANSFORMATION FOR MARKOV PROCESSES ASSOCIATED WITH SEMI-DIRICHLET FORMS?
Xinfang HAN(韓新方)Li MA(馬麗)
Department of Mathematics and Statistics,Hainan Normal University,Haikou 571158,China
ON GENERALIZED FEYNMAN-KAC TRANSFORMATION FOR MARKOV PROCESSES ASSOCIATED WITH SEMI-DIRICHLET FORMS?
Xinfang HAN(韓新方)Li MA(馬麗)?
Department of Mathematics and Statistics,Hainan Normal University,Haikou 571158,China
E-mail:xfanghan@163.com;malihnsd@163.com
Suppose that X is a right process which is associated with a semi-Dirichlet form (E,D(E))on L2(E;m).Let J be the jumping measure of(E,D(E))satisfying J(E×E?d)<∞.Let u∈D(E)b:=D(E)∩L∞(E;m),we have the following Fukushima’s decomposition ?u(Xt)??u(X0)=Mut+Nut.Defne Putf(x)=Ex[eNutf(Xt)].Let Qu(f,g)=E(f,g)+E(u,fg) for f,g∈D(E)b.In the frst part,under some assumptions we show that(Qu,D(E)b)is lower semi-bounded if and only if there exists a constant α0≥0 such that kPutk2≤eα0tfor every t>0.If one of these assertions holds,then(Put)t≥0is strongly continuous on L2(E;m). If X is equipped with a diferential structure,then under some other assumptions,these conclusions remain valid without assuming J(E×E?d)<∞.Some examples are also given in this part.Let Atbe a local continuous additive functional with zero quadratic variation. In the second part,we get the representation of Atand give two sufcient conditions forto be strongly continuous.
semi-Dirichlet form;generalized Feynman-Kac semigroup;strong continuity; lower semi-bounded;representation of local continuous additive functional with zero quadratic variation
2010 MR Subject Classifcation60J55;60J35
1 Introduction
Let E be a metrizable Lusin space and X=((Xt)t≥0,(Px)x∈E?)be a right process on E (see[11,IV,Defnition 1.8]).Suppose that X is associated with a semi-Dirichlet form(E,D(E)) on L2(E;m),where m is a σ-fnite measure on the Borel σ-algebra B(E)of E.Then,by[3, Theorem 3.22],(E,D(E))is quasi-regular.Moreover,(E,D(E))is quasi-homeomorphic to a regular semi-Dirichlet form(see[6,Theorem 3.8]).We refer the reader to[5]and[11]for the theory of Dirichlet forms.The notations and terminologies of this paper follow[5,11–13].Put D(E)Vn={u∈D(E)|u=0 q.e.on Vcn}and D(E)Vn,b=D(E)Vn∩L∞(E,m).For α>0, defne Eα(u,u):=E(u,u)+α(u,u)m,where(u,u)mmeans the product of u and u in L2(E,m).
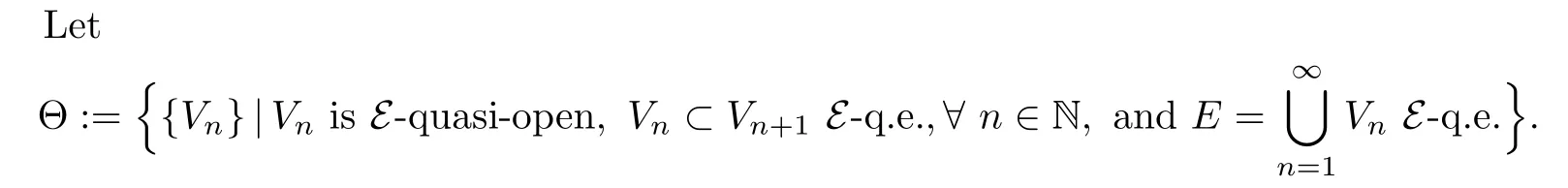
Assumption 1There exist a sequence of sets{Vn}∈Θ and a sequence of locally bounded functions{Cn}on R,such that for each n∈N,if u,v∈D(E)Vn,b,then uv∈D(E)and
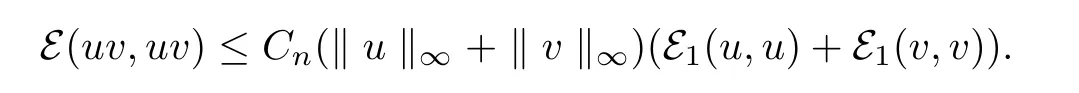
For u∈D(E)b,under Assumption 1,by[12,Proposition 2.8],we have the following Fukushima type decomposition

where?u is a quasi-continuous m-version of u,is a local martingale additive functional (abbreviated as MAF)andis a continuous additive functional(abbreviated as CAF)of zero quadratic variation.For x∈E,denote by Exthe expectation with respect to(w.r.t.)Px. Defne the generalized Feynman-Kac transformation
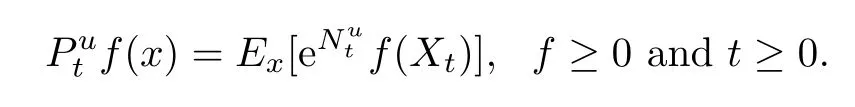
In this paper,we will investigate the strong continuity of the semigroup
The strong continuity of generalized Feynman-Kac semigroups for symmetric Markov processes was studied extensively by many people.We refer the reader to page 734 in[9]for a review.Suppose a symmetric Markov process(Xt)t≥0is associated with a Dirichlet form (E,E(E)).The researchers showed that the semigroupis strongly continuous on L2(E;m)if and only if the bilinear form(Qu,D(E)b)is lower semi-bounded.Here and henceforth

For non-symmetric Dirichlet form,Ma and Sun gave two sufcient conditions for(Put)t≥0 to be strongly continuous in[9,Theorem 1.1,Theorem 1.2].In that paper,Beurling-Deny formula and Lejan’s transform rule are used essentially.
For semi-Dirichlet form,Ma and Sun got Fukushima type decomposition for local semi-Dirichlet form in[8].Later Ma et al.generalized it to general semi-Dirichlet form in[12].Sois well-defned.It is natural to ask what’s the sufcient condition forto be strongly continuous in the setting of semi-Dirichlet form.
There is a big diference between semi-Dirichlet form and Dirichlet form.For example, in general,the domain of semi-Dirichlet form is not an algebra,the symmetric part of semi-Dirichlet form and the dual form are only positive preserving forms not Dirichlet forms,the dual semigroup is not sub-Markov.So we need to put some assumptions under the framework of semi-Dirichlet form.For u∈D(E)b,let hMuitbe the sharp bracket process of Mutandμhuibe the Revuz measure of hMuit(see[8]).
Assumption 2There are an E-nest{Fn}consisting of compact sets of E and some positive constants{Kn}such that for any n∈N,μhfi(Fn)≤KnE1(f,f)for any f∈D(E)Fn,b.
Assumption 3There exists{Vn}∈Θ such that for each n∈N,there exists a Dirichlet form(η(n),D(η(n)))on L2(Vn;m)and a constant Cn>1 such that D(η(n))=D(E)Vnand forany u∈D(E)Vn,
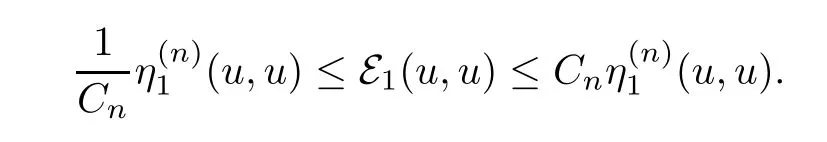
Denote by J(dx,dy)and K(dx)the jumping and killing measures of(E,D(E)),respectively (see[6]).
Now we can state the frst two main results of the paper.
Theorem 1.1Suppose that X is a right process associated with a semi-Dirichlet form (E,D(E))on L2(E;m).Let J be the jump measure of(E,D(E))satisfying J(E×E?d)<∞. Let u∈D(E)b.Then under Assumptions 2 and 3,the following two conditions are equivalent to each other:
(i)there exists a constant α0≥0 such that
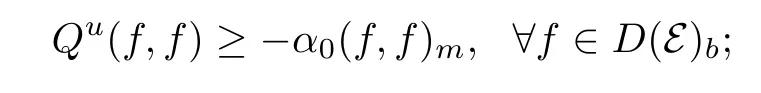
(ii)there exists a constant α0≥0 such that
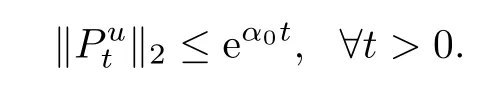
Furthermore,if one of these conditions holds,then the semigroupis strongly continuous on L2(E;m).
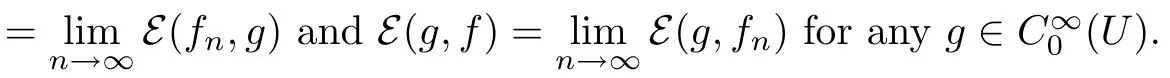
Notice that by[12],Assumption 3 implies Assumption 1 and Assumption 4.
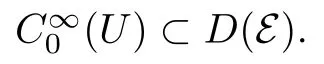
In Section 2,we give the proofs of Theorems 1.1 and 1.2.In Section 3,we will give some examples which satisfy Assumption 2 and Assumption 3.
As is well-known,a CAF of zero energy has zero quadratic variation.It is natural to ask whether the zero quadratic variation processes are at least locally of zero energy or not. For symmetric irreducible difusion process,in[14],Oshima and Yamada gave an afrmative answer.For more general Markov process associated with non-symmetric Dirichlet form,in [20],Walsh got the similar result.
In Section 4,for Markov processes associated with semi-Dirichlet forms,we will give a representation of local CAF of zero quadratic variation in terms of CAF with zero energy. Then we will study the strong continuity of generalized Feynman-Kac semigroups induced by a local CAF of zero quadratic variation.
2 Proofs of Theorems 1.1 and 1.2
By quasi-homeomorphism,we assume without loss of generality that X is a Hunt process and(E,D(E))is a regular semi-Dirichlet form on L2(E;m),where E is a locally compactseparable metric space and m is a positive Radon measure on E with supp[m]=E.We denote by?and ζ the cemetery and lifetime of X,respectively.It is known that every f∈D(E)has a quasi-continuous m-version.To simplify notation,we still denote this version by f.
The proofs of Theorems 1.1 and 1.2 are similar to those of Theorems 1.1 and 1.2 in[9].In the following,we only point out the diferences.
In[9],for u∈D(E),the Fukushima decomposition of u(Xt)?u(X0)always exists.But

may be not locally integrable and the predictable dual process Bptof Btmay not exist,so instead of u,u?:=u+|u|Eis used to defne Bt,where|u|Eis the reduce function of u on E. Under semi-Dirichlet form setting,for u∈D(E),Fukushima decomposition of u(Xt)?u(X0) exists if and only if u satisfes condition(S)(see[12,Proposition 2.8]).So in this paper,we need u∈D(E)band J(E×E?d)<∞,which guarantee that u satisfes condition(S).Since u is bounded,so Btdefned by(2.1)is locally integrable and we can substitute u?in[9]by u or treat|u|Eas 0.
Let Enbe the fne interior of some E-nest Fn.In inequalities(2.10)and(2.11)of[9],it is used that for any f∈D(E)En,b,

In fact,for non-symmetric Dirichlet form,
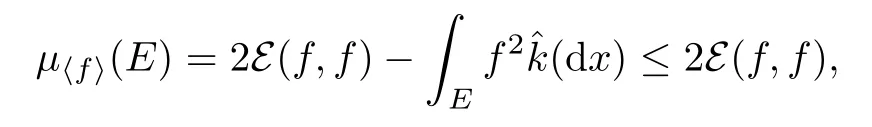
where?k(dx)is the killing measure of dual form ?E,which is also a Dirichlet form.However,for semi-Dirichlet form,the dual form is only a positive preserving form whose semi-group has no sub-Markov property,so the killing measure?k(dx)may not exist.So(2.2)may not hold in semi-Dirichlet form setting.For example,

By[10,Remark 2.2(ii)],(E,D(E))is a regular local semi-Dirichlet form but not a Dirichlet form.Let Fn=[1n,1?1n],then{Fn}is an E-nest and En=(1n,1?1n)is the fne interior of Fn.For any f∈D(E)En,b,
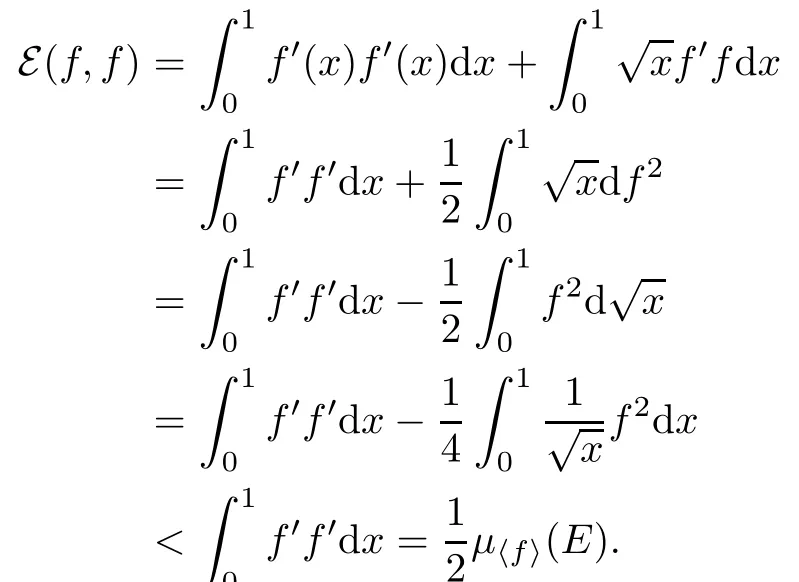

Denote by?E the symmetric part of E.The jumping measure?J and killing measures?K of the symmetric part(?E,D(E))are used to in(2.31)of[9].In semi-Dirichlet form setting,(?E,D(E)) is not a Dirichlet form,so?J and?K don’t exist.We can solve this by Assumption 2, Z

Notice in(2.32)of[9],it is used that

For semi-Dirichlet form,we can use Assumption 2 to overcome this difculty,
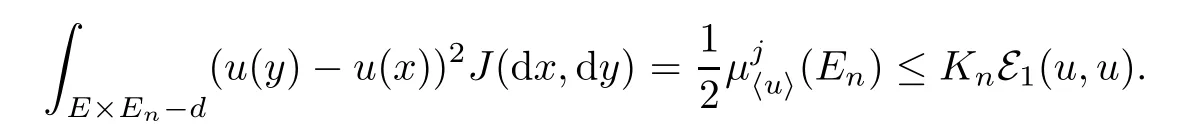
So Assumption 2 is really needed in this paper.
LeJan’s transformation rule and Lemma 2.4 of[9]are used in the proof of Theorem 1.1 in[9].We have corresponding results in semi-Dirichlet form setting(see[17,Theorem 3.3, Theorem 3.5])under Assumption 3.4 in[17].Our Assumption 3 guarantees the Assumption 3.4 in[17],so we can use the results of[17,Theorem 3.3,Theorem 3.5]and get Theorem 1.1.
Beurling-Deny formula of Non-symmetric Dirichlet forms are used in the proof of Theorem 1.1 in[9].We have similar formula for semi-Dirichlet forms(see[6,Theorem 4.8]).Since u∈D(E)b,J(E×E?d)<∞in Theorem 1.1,so we can use[6,Theorem 4.8]directly.
The expression of(E,D(E))is used in the proof of Theorem 1.2 in[9].In semi-Dirichlet form setting,under Assumption 4,(E,D(E))has similar expression(see[17,Theorem 1.4]).So we get Theorem 1.2.
In the proof of main theorems(p.750 of[9]),it is used that∪n≥1D(E)Enis dense in D(E). For semi-Dirichlet form,our results are constructed under Assumption 2 and Assumption 3 or Assumption 1 and Assumption 2,so we need revise the set Enand prove that∪n≥1D(E)Enis dense in D(E).Let{Fn}be the compact sets in Assumption 2 and{F′n}be the compact sets in p.737 of[9],we should takeLetbe the sets in Assumption 1 or Assumption 3.Put[7,Lemma 3.6],is dense in D(E).
Remark 2.1Letμ=μ+?μ?,whereμ+andμ?are smooth measures,be positive CAFs(PCAFs in short)with Revuz measureμ+andμ?,respectively,let Aμt:=Defne
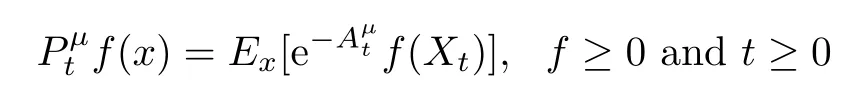
and
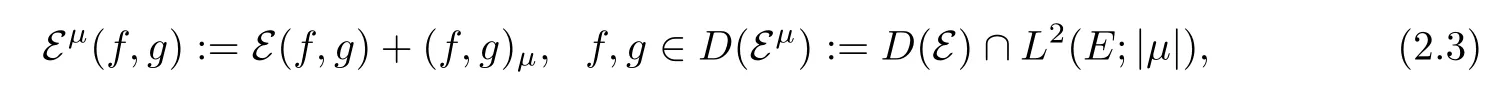
then by localization method,similar to the proofs of Theorem 1.1 and Theorem 1.2,we can show the following two conditions are equivalent to each other
(i)there exists a constant α0≥0 such that
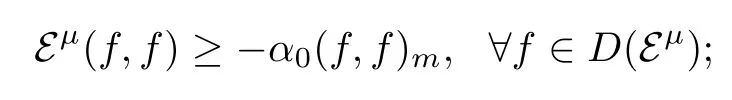
(ii)there exists a constant α0≥0 such that

Furthermore,if one of these conditions holds,then the semigroupis strongly continuous on L2(E;m).This result extends[9,Remark 2.7].
3 Some Examples
In this section,we will give some examples which satisfy Assumption 2 and Assumption 3.
Example 3.1In this example,we study the generalized Feynman-Kac semigroup for the semi-Dirichlet form given in[8]and[15].
Let d≥3,U be an open subset of
we defne

Assume that
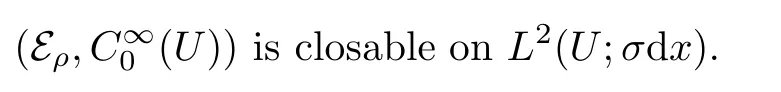
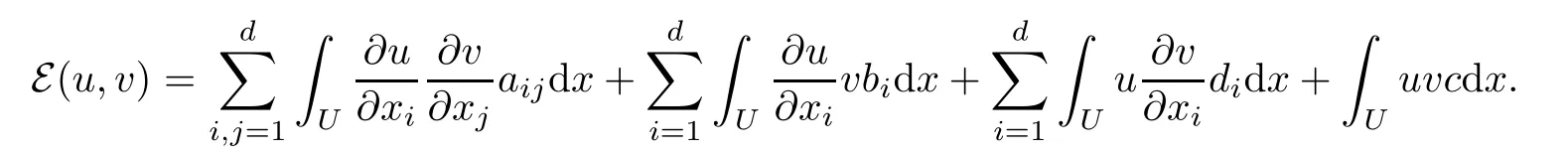
We denote vector d by d.Let b= β+γ.Then,by[15,Theorem 1.2],under some conditions on aij,b,d,β,γ and c,there exists α>0 such that(Eα,C∞0(U))is closable on L2(U;dx)and its closure(Eα,D(Eα))is a regular local semi-Dirichlet form on L2(U;dx).Defne ηα(u,u):=Eα(u,u)?Rh▽u,βiudx for u∈D(Eα).By[15,Theorem 1.2(ii)and(1.28)],we know(ηα,D(Eα))is a Dirichlet form and there exists ?∈(0,1)such that for any u∈D(Eα),
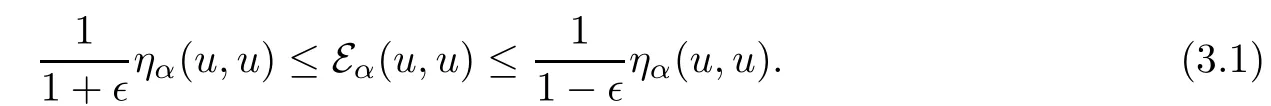
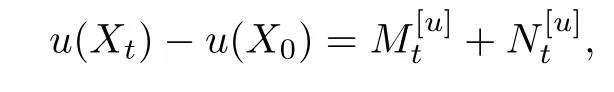
Let X be the Markovprocess associated with(Eα,D(Eα)),u∈D(Eα)b,then u(Xt)has Fukushima’s type decompositions a locally square integrable MAF andis a locally CAF of zero quadratic variation.By (3.1),Assumption 3 holds.Notice there is no jump part in expression of E,so J(E×E?d)<∞holds automatically.Next,we check Assumption 2.Since
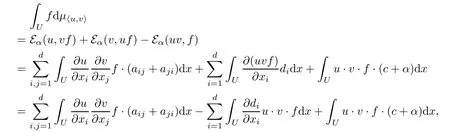
it follows that
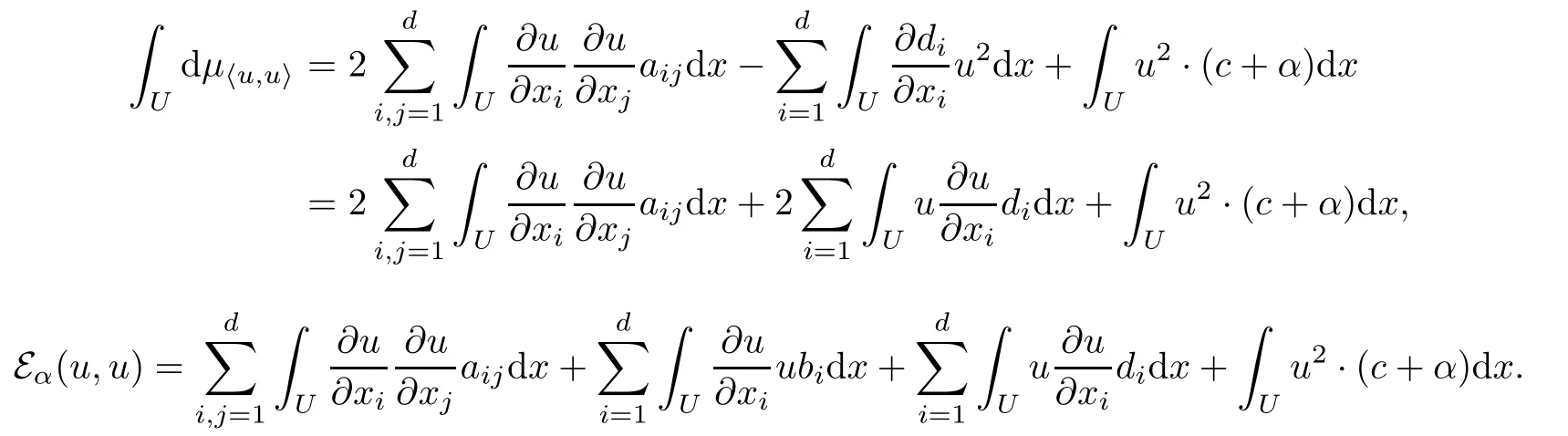
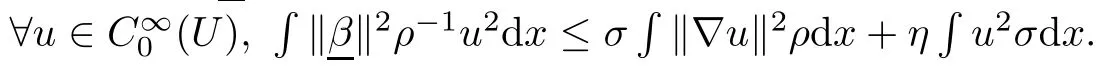


Hence Assumption 2 holds.LetThen,forwe have

Suppose that the following condition holds.
(A4)There exists a constant α0≥0 such that
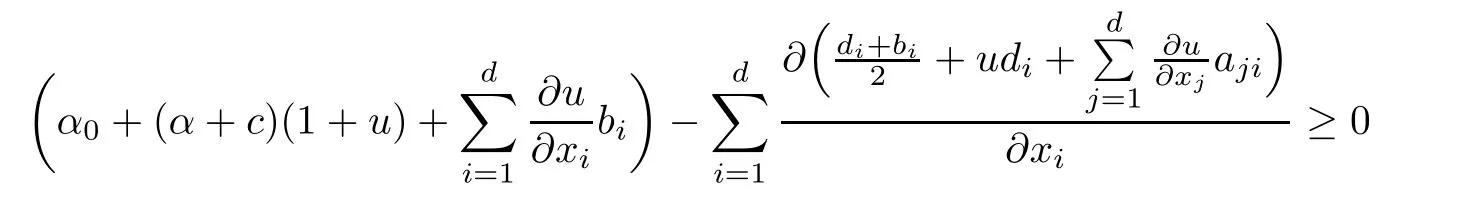
in the sense of Schwartz distribution.
Then Qu(f,f)≥?α0(f,f)for any f∈C∞0(U)and thus for any f∈D(E)bby approximation.
Example 3.2(see[4]and[16]) Let(E,d)be a locally compact separable metric space, m a positive Radon Measure on E with full topological support,and k(x,y)a nonnegative Borel measurable function on{(x,y)∈E×E|x 6=y}.Set ks(x,y)=12(k(x,y)+k(y,x)) and ka(x,y)=12(k(x,y)?k(y,x)).Denote by Clip0(E)the family of all uniformly Lipschitz continuous functions on E with compact support.Suppose that the following conditions hold

and

In fact
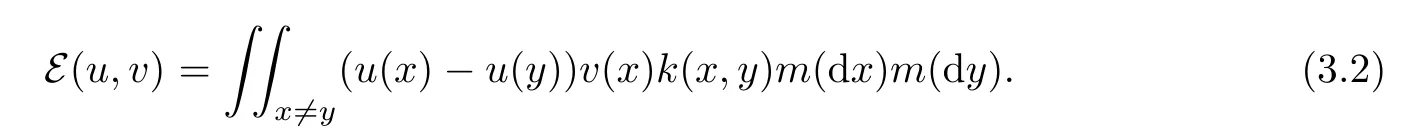

Let D(E)be the η1-closure ofThen by[4,Theorem 2.1],(Eβ0,D(E))be a regular semi-Dirichlet form on L2(E,m).Moreover,Assumption 3 holds.
Next we check Assumption 2.By(3.2),
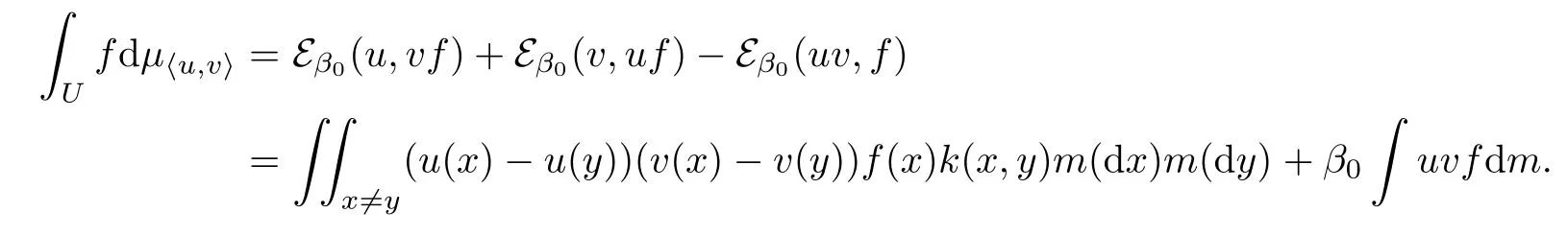
Hence
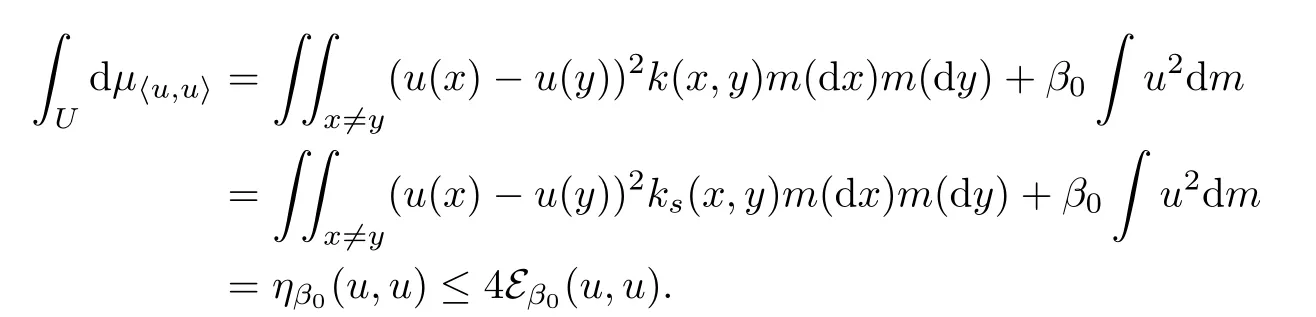
So Assumption 2 holds,
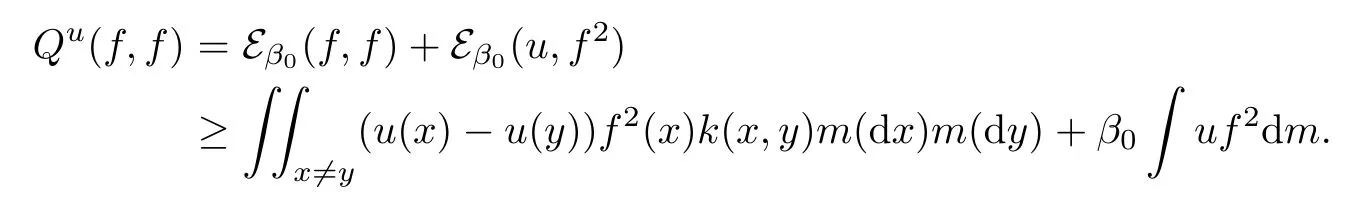
(B.III)There exists a constant α0≥0 such that
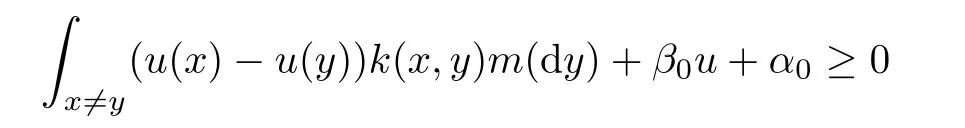
in the sense of Schwartz distribution.
If(B.III)holds,then Qu(f,f)≥?α0(f,f)mfor any f∈Clip0(E)and thus for any f∈D(E)bby approximation.
Let X be aμ-tight special standard jump process associated with(Eβ0,D(E))and(Put)t≥0be the generalized Feynman-Kac semigroup induced by u.In Theorem 1.1,J(E×E?d)<∞is used in the proof of
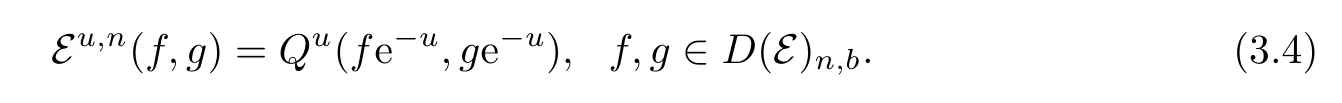
However,in this example,we can get(3.4)directly by the expression of(Eβ0,D(Eβ0))though J(E×E?d)<∞ may not be true here.Hence,by Theorem 1.1,if(B.III)holds,thenis a strongly continuous contraction semigroup on L2(E;m).
Example 3.3(see[18]) Let d>3,G be an open set of Rd.Defne for u,v∈C10(G),
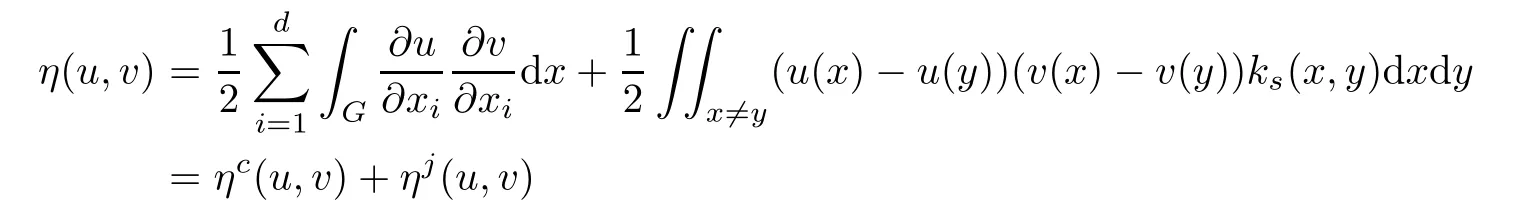
and
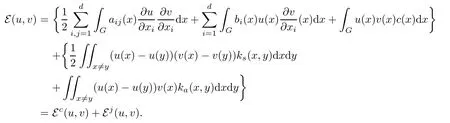
We refer to[18]for the conditions on aij,b,c,d,ksand ka.By previous example,we know
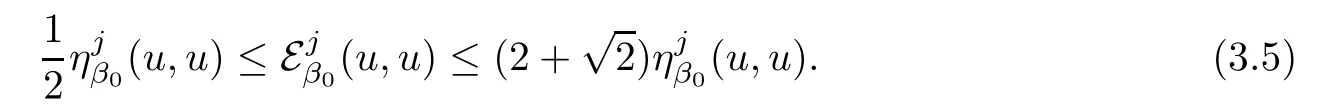
By the proof of[18,Proposition 3.1 and Proposition 3.2],there exist some constants K1>0 and C>0 such that

So
If
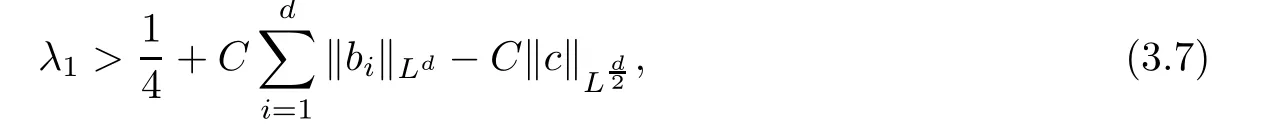
then
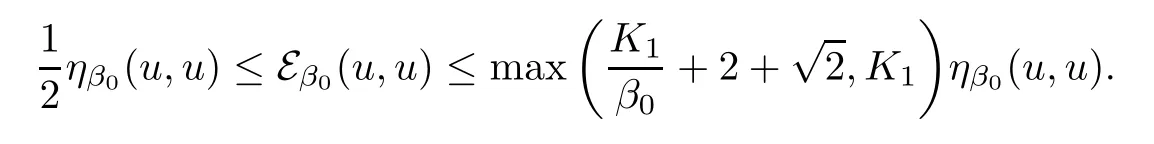
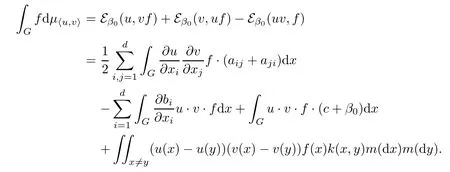
Let1q+1d=12,by Cauchy-Schwarz’s inequality,
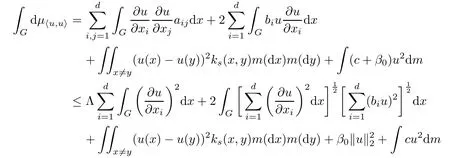
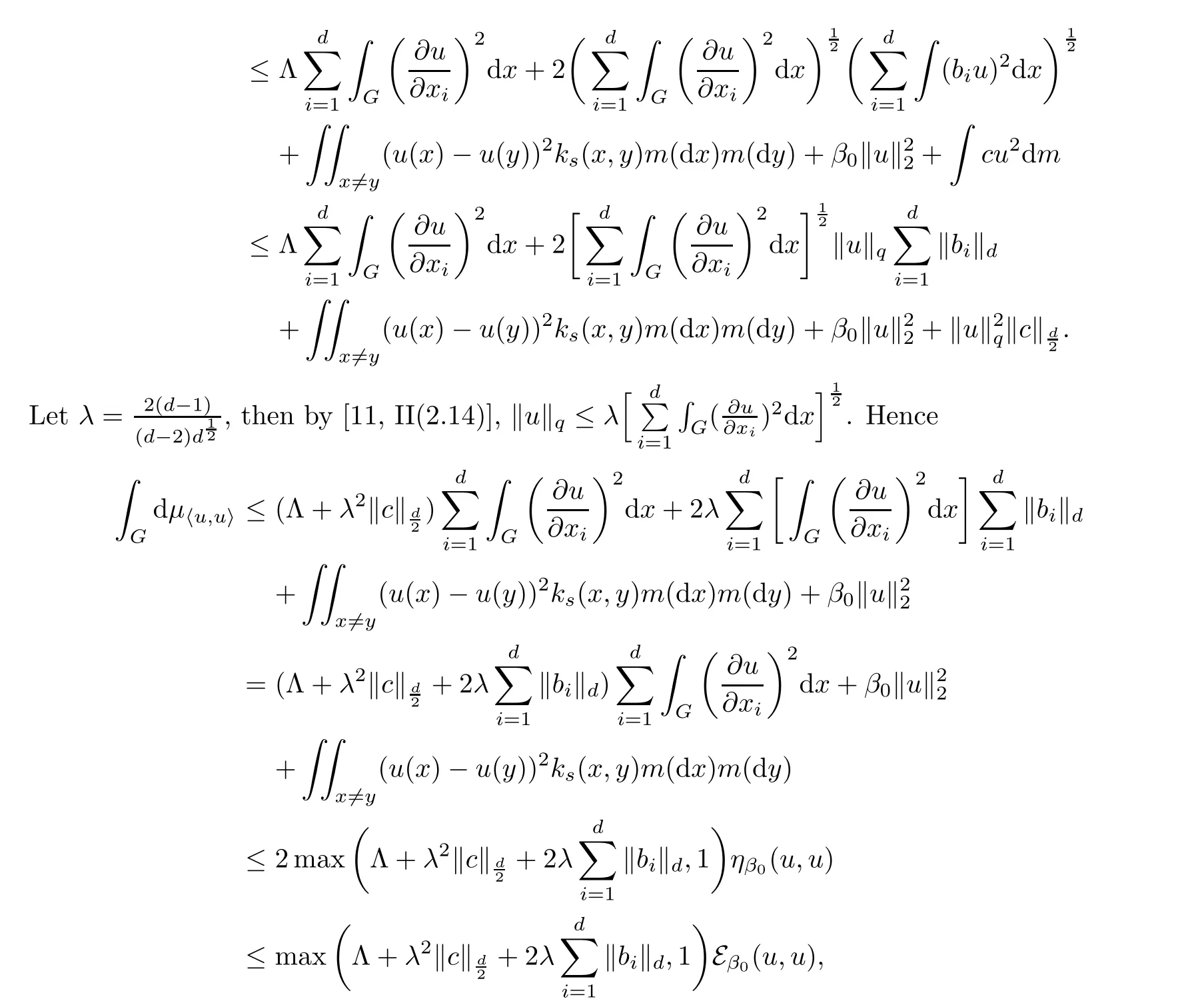
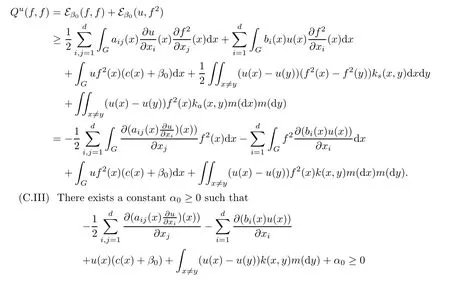
and Assumption 2 holds.in the sense of Schwartz distribution.
If(C.III)holds,then Qu(f,f)≥?α0(f,f)for any f∈Clip0(G)and thus for any f∈D(E)bby approximation.
Let X be aμ-tight special standard jump process associated with(Eβ0,D(E))and(Put)t≥0be the generalized Feynman-Kac semigroup induced by u.If(C.III)and(3.7)holds,then by Theorem 1.2,is a strongly continuous contraction semigroup on L2(G;dx).
4 Representation of Local CAF with Zero Quadratic Variation
In this section,we consider representation of local CAF with zero quadratic variation under semi-Dirichlet form setting.For a quasi-open set V,let(EV,D(EV))be the part form of (E,D(E))on L2(V;m),then D(EV)=D(E)V.Let?GVαbe the co-resolvent of(EV,D(E)V) and XVbe the part process associated with(EV,D(E)V).Fix a function φ∈L1(E;m)with 0<φ≤1 m-a.e.,thenRVφ2dm ≤ REφ2dm ≤ REφdm<∞,hence φ∈L2(V,m).Put ˉhV=?GV1φ.For an AF Atof XV,defne

whenever the limit exists in[0,∞],
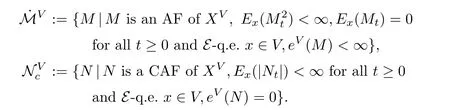
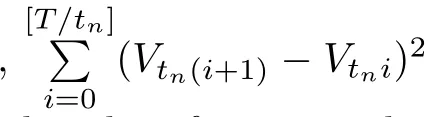
Theorem 4.1Let A be a local CAF of zero quadratic variation.Then,there exist a E-nest of fnely open sets{Gn}n∈N,a sequence{un}?D(E)Gn,band a nest of fnely open sets {Vn}n∈Nsuch that Vn?Gnand
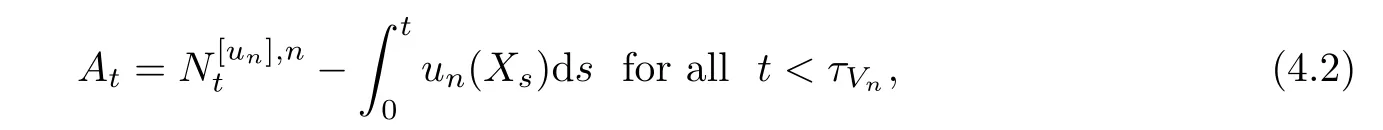
Px-a.s.for every x except in a exceptional set.Hereandis the zero energy part of Fukushima’s decomposition with respect to unand XGn.
ProofThe proof is similar to that of[19,Theorem 1.1].We only list the diference here. In[19,Lemma 3.4],the co-semigroup?Ptand 1-co-resolvent?R1are expressed in terms of dual process?Xt,which dose not exist for semi-Dirichlet form.Notice?Ptand?R1still exist and are positivity preserving operators.Let g(x)= ?R1φ(x),then g is 1 co-excessive function.Hence when 0 So[19,Lemma 3.4]still holds in semi-Dirichlet form case. Then by the proof of[19,Theorem 1.1],vnis bounded,Mnis a MAF of Xnand there exists {H0n}n∈N∈Θ such that for any n,IH0n?Mn∈ ˙MH0nand H0n? Gn.For fxed n∈N and anyLetthen h?is 1-co-excessive function with respect toof relatively compact set such that h?is bounded on H?n.Without loss of generality,assumeAlso,we can constructin Θ and sequence{gn}n∈Nand{hn}n∈Nin D(E)such that for all n∈N, Notice h?is 1-co-excessive function with respect to P0t,so and Notice gn∈D(E)H1nand h?is bounded up by Cnon H1n,so Since gn,h?∈D(E)H0n,so Let un=Rn1vn?γn+wn?Rn1wn,notice vnand gnare bounded,Rn1is sub-Markov and wn=vngn,so Rn1vn+wn?Rn1wnis bounded.By revising the nest?Gnsuch that I?Gnμn1and I?Gnμn2belongs to S00(En)instead of S0(En)in the proof of[19,Theorem 1.1],we can get γn∈D(E)Gn,b.Hence un∈D(E)Gn,band Px-a.e.for q.e.x∈E on{t<τVn}, When s≤t<τVn,Xns=Xs,so let Gn=Gn,we get(4.2). Defne Theorem 4.2If(E,D(E)Gn)and its jumping measure Jnsatisfes the conditions of Theorem 1.1 or Theorem 1.2,then the following two are equivalent. (i)There exists a constant α0≥0 such that (ii)There exists a constant α0≥0 such that Further,if for any n∈N,(i)or(ii)holds,thenis strongly continuous. ProofBy section 2,we know(i)and(ii)are equivalent and they impliesare strongly continuous by looking Gnas E,Vnas En,unas u,undm as dμand If(ii)holds,then for?g∈L2(E;m), Since g∈L2(E;m)is arbitrary,we get Since f and n are arbitrary,is strongly continuous on L2(E;m).The proof is completed. AcknowledgementsWe thank Professor Wei Sun for helpful discussions. [1]Albeverio S,Ru-Zong F,R¨ockner M,Stannat W.A remark on coercive forms and associated semigroups. Oper Theory Adv Appl,1995,78:1–8 [2]Chen C Z,Ma Z M,Sun W.On Girsanov and generalized Feynman-Kac transfromations for symmetric Markov processes.Infn Dimens Anal Quantum Probab Relat Top,2007,10:141–163 [3]Fitzsimmons P J.On the quasi-regularity of semi-Dirichlet forms.Potential Anal,2001,15:158–185 [4]Fukushima M,Uemura T.Hunt processes generated by lower bounded semi-Dirichlet forms.Ann Probab, 2012,40:858–889 [5]Fukushima M,Oshima Y,Takeda M.Dirichlet Forms and Symmetric Markov Processes.Berlin:Walter de Gruyrer,1994 [6]Hu Z C,Ma Z M,Sun W.Extensions of L′evy-Khintchine formula and Beurling-Deny formula in semi-Dirichlet forms setting.J Funct Anal,2006,239:179–213 [7]Kuwae K.Maximum principles for subharmonic functions via local semi-Dirichlet forms.Can J Math,2008, 60:822–874 [8]Ma L,Ma Z M,Sun W.Fukushima’s decomposition for difusions associated with semi-Dirichlet forms. Stoch Dyn,2012,12:1250003–1250031 [9]Ma L,Sun W.On the generalized Feynman-Kac transformations for nearly symmetric Markov processes. J Theor Probab,2012,25:733–755 [10]Ma Z M,Overbeck L,R¨ockner M.Markov processes associated with semi-Dirichlet forms.Osaka J Math, 1995,32:97–119 [11]Ma Z M,R¨ockner M.Introduction to the Theory of(Non-Symmetric)Dirichlet Forms.Berlin:Springer-Verlag,1992 [12]Ma Z M,Sun W,Wang L F.Fukushima type decomposition for semi-Dirichlet forms.Preprint, http://arxiv.org/abs/1402.4341 [13]Oshima Y.Semi-Dirichlet Forms and Markov Processes.Walter de Gruyter,2013 [14]Oshima Y,Yamada T.on some representations of continuous additive functionals locally of zero energy.J Math Soc Jpn,1984,36(2):315–339 [15]R¨ockner M,Schmuland B.Quasi-regular Dirichlet forms:examples and counterexamples.Can J Math, 1995,47:165–200 [16]Schilling R L,Wang J.Lower bounded semi-Dirichlet forms associated with L′evy type operators.Festschrift Masatoshi Fukushima,2015:507–526 [17]Sun W,Zhang J.L′evy-Khintchine type representation of Dirichlet generators and semi-Dirichlet forms. Forum Math,2015,27:3111–3148 [18]Uemura T.On multidimensional difusion processes with jumps.Osaka J Math,2014,51(4):969–993 [19]Walsh A.On a representation of additive functionals of zero quadratic variation.Potential Anal,2013, 38(4):1173–1186 [20]Walsh A.Stochastic integration with respect to additive functionals of zero quadratic variation.Bernoulli, 2013,19B(5):2414–2436 ?Received June 2,2015;revised October 2,2015.This paper is supported by NSFC(11201102,11326169, 11361021)and Natural Science Foundation of Hainan Province(112002,113007). ?Corresponding author:Li MA.

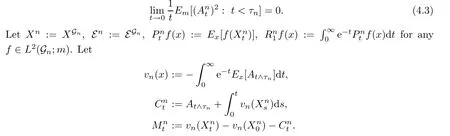

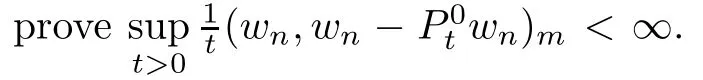

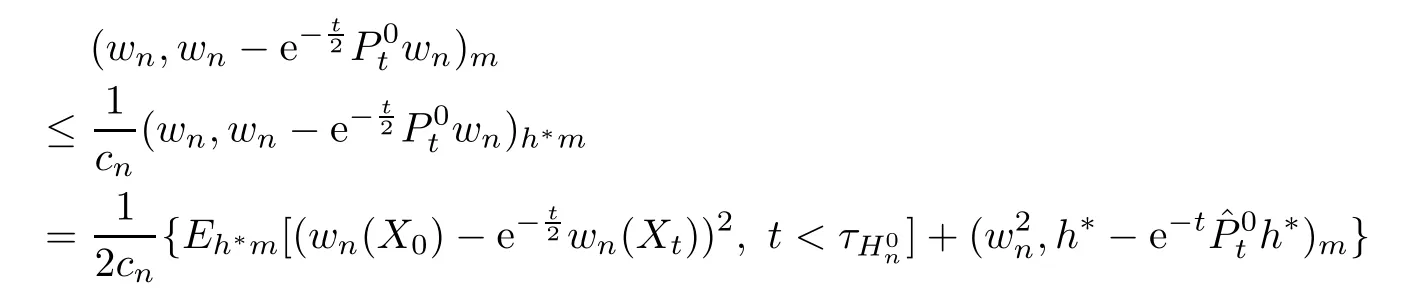
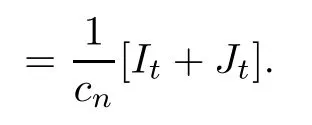
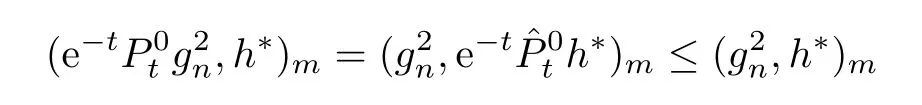
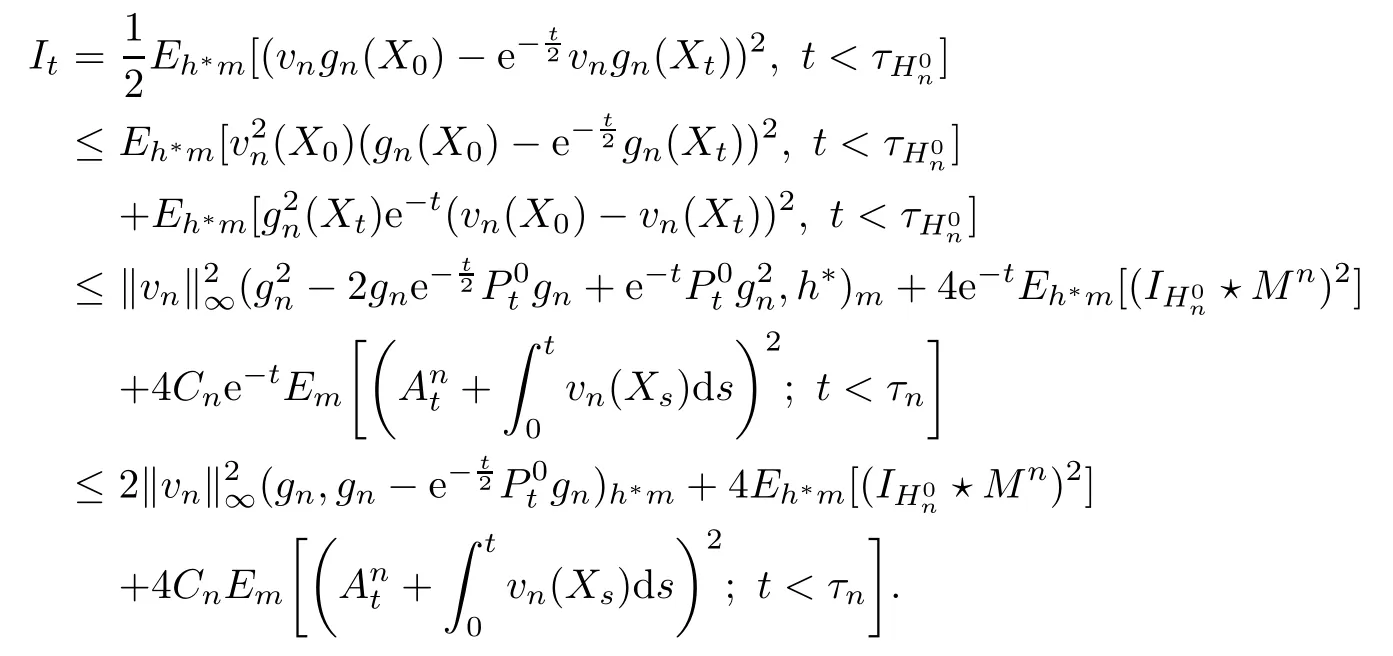
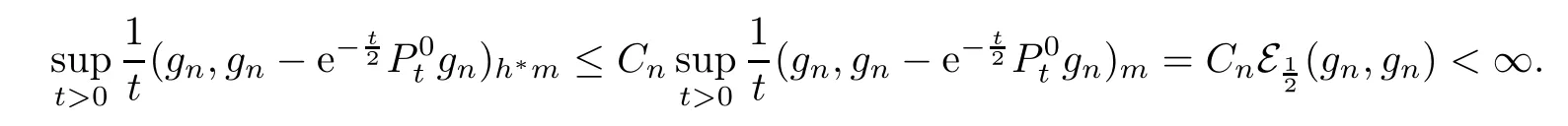
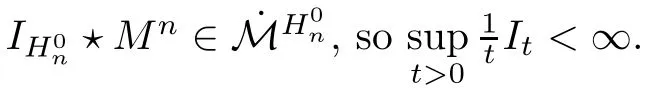

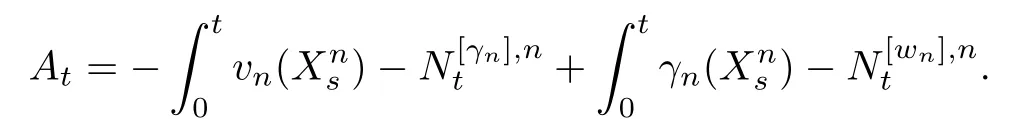

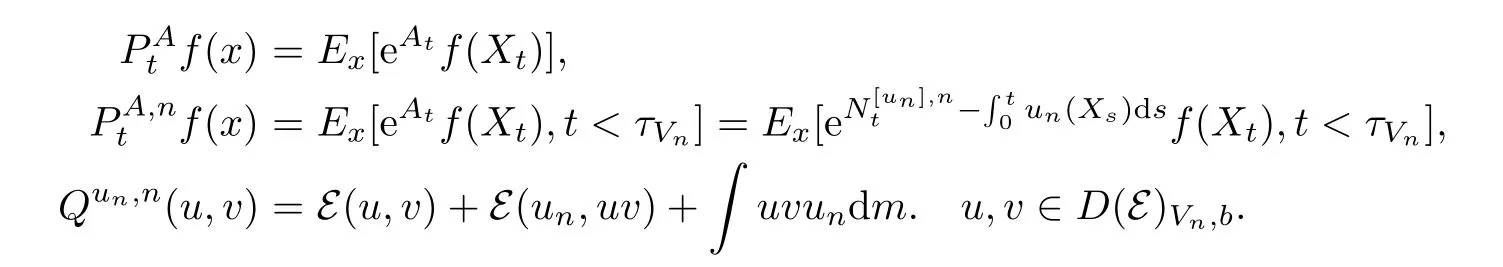

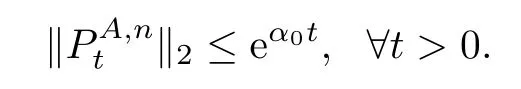
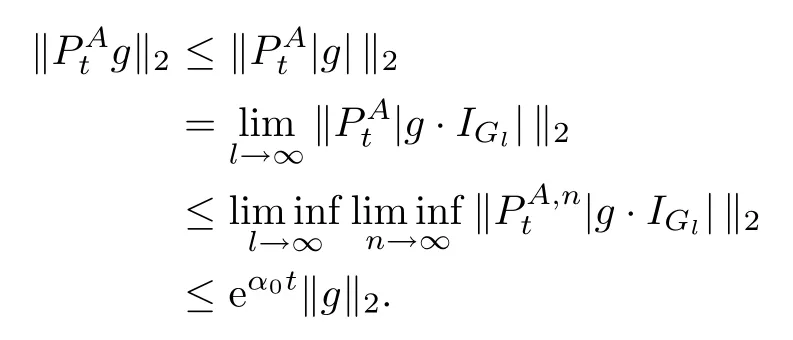

 Acta Mathematica Scientia(English Series)2016年6期
Acta Mathematica Scientia(English Series)2016年6期
- Acta Mathematica Scientia(English Series)的其它文章
- NEW LOWER BOUNDS FOR LEE DISCREPANCY ON TWO AND THREE MIXED LEVELS FACTORIALS?
- THREE SOLUTIONS FOR A FRACTIONAL ELLIPTIC PROBLEMS WITH CRITICAL AND SUPERCRITICAL GROWTH?
- SHARP ESTIMATES OF ALL HOMOGENEOUS EXPANSIONS FOR A SUBCLASS OF QUASI-CONVEX MAPPINGS OF TYPE B AND ORDER α IN SEVERAL COMPLEX VARIABLES?
- MULTIPLICITY RESULTS FOR A NONLINEAR ELLIPTIC PROBLEM INVOLVING THE FRACTIONAL LAPLACIAN?
- EXISTENCE AND UNIQUENESS OF NON-TRIVIAL SOLUTION OF PARABOLIC p-LAPLACIAN-LIKE DIFFERENTIAL EQUATION WITH MIXED BOUNDARIES?
- PROPERTIES OF THE MODIFIED ROPER-SUFFRIDGE EXTENSION OPERATORS ON REINHARDT DOMAINS?
