Integration of the Coupled Orbit-Attitude Dynamics Using Modified Chebyshev-Picard Iteration Methods

Xiaoli Bai,John L.Junkins

Integration of the Coupled Orbit-Attitude Dynamics Using Modified Chebyshev-Picard Iteration Methods

Xiaoli Bai1,John L.Junkins2

This paper presents Modified Chebyshev-Picard Iteration(MCPI)methods for long-term integration of the coupled orbit and attitude dynamics.Although most orbit predictions for operational satellites have assumed that the attitude dynamics is decoupled from the orbit dynamics,the fully coupled dynamics is required for the solutions of uncontrolled space debris and space objects with high area-to-mass ratio,for which cross sectional area is constantly changing leading to significant change on the solar radiation pressure and atmospheric drag.MCPI is a set of methods for solution of initial value problems and boundary value problems.The methods refine an orthogonal function approximation of long-time-interval segments of state trajectories iteratively by fusing Chebyshev polynomials with the classical Picard iteration and have been applied to multiple challenging aerospace problems.Through the studies on integrating a torque-free rigid body rotation and a long-term integration of the coupled orbit-attitude dynamics through the effect of solar radiation pressure,MCPI methods are shown to achieve several times speedup over the Runge-Kutta 7(8)methods with several orders of magnitudes of better accuracy.MCPI methods are further optimized by integrating the decoupled dynamics at the beginning of the iteration and coupling the full dynamics when the attitude solutions and orbit solutions are converging during the iteration.The approach of decoupling and then coupling during iterations provides a unique and promising perspective on the way to warm start the solution process for the longterm integration of the coupled orbit-attitude dynamics.Furthermore,an attractive feature of MCPI in maintaining the unity constraint for the integration of quaternions within machine accuracy is illustrated to be very appealing.

Orbit propagation, orbit-attitude dynamics, Modified Chebyshev-Picard Iteration(MCPI)Methods.

1 Introduction

A population of space objects estimated to have high area-to-mass ratio(HAMR)have been reported recently[Schildknecht,Musci, Ploner,Beutler,Flury,Kuusela,Cruz and Palmero(2004);Schildknecht, Musci,Ploner,Flury,Kuusela,Cruz,and Palmero(2003)].Such objects are initially found in GEO-like orbits and later are also confirmed from statistical analysis on the debris of the Fengyun-1C breakup as well as the Cosmos 2251 fragments[Anselmo and Pardini(2010);Pardini and Anselmo(2009)].The original discovery of these “kite-like”area to mass ratio(AMR)objects with AMR larger than 1m2/kg was quite surprising,while more studies have confirmed that a primary origin of these HAMR objects is from breakups or surface degradation.Since most of these objects transit through the orbits of Geosynchronous(GEO)satellite,prediction of their orbit with high accuracy,or more to the point,with realistic uncertainty in their orbit,is important for collision avoidance.It is also necessary to make long-term prediction,usually a few days in advance,such that the required orbit maneuvers for the operational GEO satellite can be scheduled and executed optimally.Since models of these objects using simplistic “cannonball”drag and ignoring attitude dynamics lead to unrealistic results,it is important to properly couple the dynamics.It is well known that these equations are frequently stiff,and possess low frequencies associated with orbital dynamics and high frequencies associated with attitude dynamics.We present a computationally efficient method for long-term six-degrees-of-freedom propagation of the state of such HAMR objects with high accuracy.

To characterize the orbits of these HAMR objects is challenging.On one hand,most of these objects are tracked by on-ground telescope through which the optical observations are not only sparse but also dim with time-varying light intensity(due to the observation geometry,lighting,albedo variations,and especially,the attitude relative to the sensor line of sight).On the other hand,the orbits and attitude of these objects are highly perturbed by non-conservative forces and moments especially solar radiation pressure(SRP),comparable to how the orbits of the low Earth orbit(LEO)objects could be highly perturbed by the atmospheric drag.The difficulty to get quality measurements together with the highly unstable orbits of these HAMR objects lead to large model uncertainties about these objects,including their orbit,attitude,mass,shape,reflection and thermal properties.In addition to these challenges,a computationally demanding task for orbit propagation of these objects is the necessity to integrate their orbit dynamics and attitude dynamics simultaneously,which is the specific topic that this paper aims to address.

For a rigid space object,orbit dynamics describes its translational motion of the center of the mass and attitude dynamics represents its rotational motion about its center of mass.Although these two types of motion are naturally coupled via SRP,atmospheric drag,gravity gradient,as well as Earth’s magnetic field,the traditional approach is to integrate the attitude dynamics and orbit dynamics separately.This practice is well-grounded for many situations.For example,the attitude of the operational spacecraft is normally stabilized either actively or passively,so the attitude dynamics is naturally solved separately from orbit dynamics.Additionally most of spacecraft has a low AMR.For these objects,although the orbital motion affects the attitude motion,the effect of the attitude motion on the orbit motion is small and frequently insignificant,so the orbit motion can be integrated first and then we can solve for the attitude.However,for HAMR objects these situations do not hold and the orbit dynamics and the attitude dynamics are frequently highly coupled and may have time-varying AMR.

Numerically integrating the coupled orbit-attitude dynamics is demanding because the attitude dynamics usually changes on a much faster time-scale than the orbit dynamics.Using Runge-Kutta type of methods,perhaps the most popular numerical integration approach,the small step size required by the attitude dynamics will have to be adopted to integrate the orbit dynamics which makes the orbital integration very slow.A few studies have focused on the semi-coupled approaches.Woodburn and Tanygin propose using an Encke-type correction method to account for the effect of the attitude dynamics on the orbit dynamics,on the assumptions that the differences between the higher order perturbations in the main orbit integration and the Encke correction are negligible[Woodburn(2001)].However,significant errors could exist when using this approach for highly perturbed objects because the correction is only forced on the correction step but not the full solution.In a recent paper by Früh,Kelecy,and Jah,the orbit and attitude are integrated separately but are recoupled according to the value of either Shannon entropy or Kullback-Leibler divergence[Früh,Kelecy,and Jah(2013)].For the test case of a uniform plate,the entropy saturates after the first few integration steps and thus could not track the attitude changes but the Kullback-Leibler divergence approach is shown to achieve high accuracy.The methodology to pick the threshold to trigger the couple phase and decouple phase is left as a future work in the paper.Of special interest is the unified state models originally proposed by Altman that use quaternions to describe attitude and velocity-hodograph parameters to describe the size and shape of the orbits[Altman(1975)].Such models have been used for tracking observations and orbit determination[Raol and Sinha(1985);Vittaldev and Naeije(2012)].A few new forms have also been recently developed[Shuster(1993)].Although the current paper is not using the unified state models,we expect that further extension of the present to consider these state variables would be most interesting.

In this paper, we propose using Modified Chebyshev-Picard Iteration (MCPI) methods for long-term integration of the coupled orbit and attitude dynamics [Bai (2010);Baiand Junkins(2011);Baiand Junkins(2011);Younes(2013);Macomber(2015)].MCPI is a set of parallel-structured methods for solution of initial value problems and boundary value problems,developed in Bai’s dissertation.The methods approximate the solution of the differential equations through Chebyshev polynomials and then utilize Picard iterations to solve for the polynomial coefficients.MCPI methods have proven to be computationally efficient for solving many challenging astrodynamics problems:MCPI methods are shown to be 10-100 times faster for given RK4,RK5,RK45 while achieving 10 times better accuracy before parallelization,10 times faster than Runge-Kutta-Nystrom 12th–10th(RKN1210)using a serial machine,competitive with Battin’s semi-analytical method to solve the Lambert’s problem,and achieved 30 times speedup over pseudospectral method for solving an optimal control problem.These selected results are for particular applications,and the MCPI methods require problem-specific tuning.However,the methodology is rapidly maturing,and Macomber’s recent dissertation[Macomber(2015)]includes methods for automatic tuning the segment intervals and order of the Chebyshev approximations.More recently,the improved MCPI achieved one order of magnitude speedup over Gauss-Jackson 8th order.Notice all of these are achieved on a serial computer.MCPI is well suited for parallelization,and given a particular computer architecture,additional orders of magnitude speedup can be achieved.MCPI has been recognized recently as a“promising and parallelizable method for orbit propagation”by National Research Council[Nielsen,Alfriend, Bloomfield,Emmert,Guo,Maclay,and Saari(2012)].

As MCPI has already proven superior to a variety of Runge-Kutta methods for orbit propagation,we choose to study the potential for computational savings when using MCPI for long-term coupled orbit-attitude dynamics integration.Since the attitude dynamics is represented by first-order differential equations,for which neither the Gauss-Jackson nor RKN1210 are applicable,we compare MCPI with Runge-Kutta methods using Dormand and Prince’s 8–7th order formulas(RK78)[Prince and Dormand(1981)].We emphasize that there exist other computational methods such as the sympletic integrator which conserves the system energy[Fahnestock,Lee,Leok,McClamroch,and Scheeres(2006)]and the dual-quaternion approach which uses a single dual number quaternion vector to described both translational and rotational motion but so far only has been developed for rather simple models but not high fidelity models[Park,Park,Park and Kim(2013)].It is the ability of MCPI to solve general different equations that suggests it should be investigated to solve for the coupled attitude and orbits of HAMR objects which involve large perturbations.

The rest of the paper is organized as follows.Background for the current study is presented in the next section.We describe the orbit dynamics and the attitude dynamics first,from which the coupled orbit-attitude dynamics will be illustrated.Two sets of simulation results are shown next.First we use 1-day integration of the torque-free motion as an example to illustrate the capability of MCPI for longterm integration of the attitude dynamics.Second we use 10-day orbital-attitude integration to demonstrate MCPI’s performance for long-term coupled dynamics integration.Finally,conclusions are drawn and future work is discussed.

2 Background

2.1 Orbit dynamics

where a is the acceleration determined from the governing physics forces.For an object orbiting around the Earth, a includes the effects from Earth gravity,atmospheric drag,SRP,third body perturbations,and a few other small effects such as tides and albedo.Since the major perturbation on HAMR objects are SRP,we focus on the Earth gravity and SRP in the current paper,leading toPoint-mass Earth gravitation model is used,such that

where μEis the Earth gravitational constant and

For an object consisting of N flat plates,the acceleration due to SRP for the ithplate surface can be expressed as

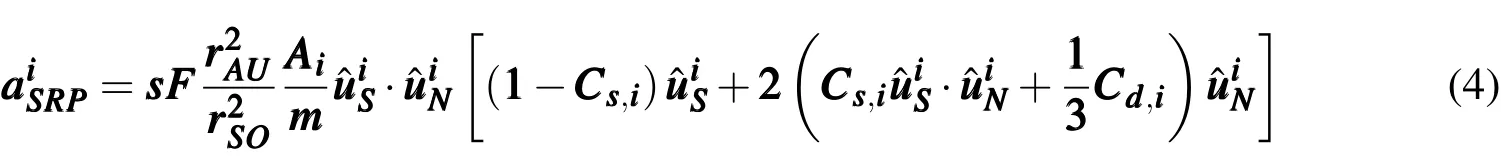
2.2 Attitude dynamics

The rotational motion of the space object idealized as a collection of rigid flat plates is represented by its angular velocity and attitude.Euler equations provide the differential equations to solve for the angular velocity,in the form

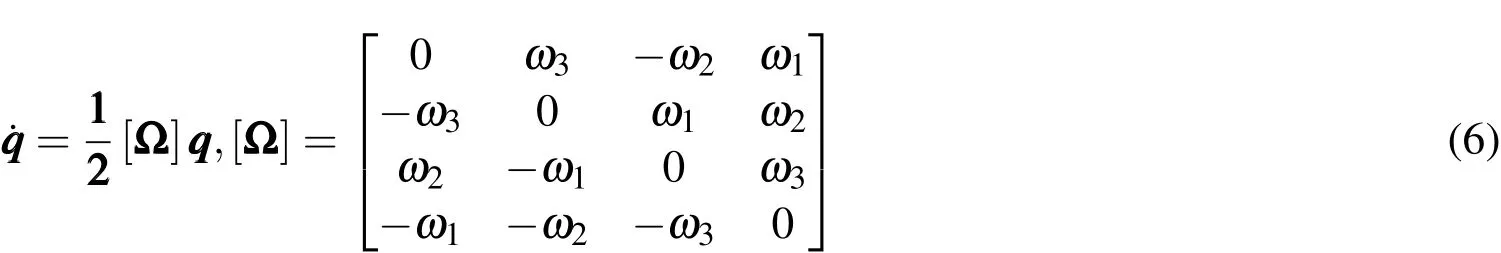
The coupling between the orbit dynamics and attitude dynamics is illustrated through Eq.4 and Eq.5.On one hand,the change of orbit will change the distance of the object to the Sun,which will change solar radiation pressure and further changes the solar radiation torque,thus effecting on the attitude dynamics.On the other hand,the change of attitude will change the projected surface area and further change the acceleration due to SRP,thus effecting on the orbit dynamics.For objects with high area to mass ratio,the change of the SRP could be significant,leading to the strong coupling between the orbit dynamics and attitude dynamics.

2.3 Modified Chebyshev-Picard Iteration

Original development on MCPI can found in references[Bai(2010);Bai and Junkins(2011);Bai and Junkins(2011)]and more recent studies can be found in references[Younes(2013);Macomber(2015)].A few basic concepts on MCPI are listed below for the convenience of the readers.

(i)MCPI are parallel-structured methods for solving both initial value problems and boundary value problems.

(ii)MCPI methods use Chebyshev polynomials to approximate the solutions.The order of the Chebyshev polynomials MCPI used is called the order of MCPI.(iii)MCPI methods normally use a much larger step size(called segment length)than the Runge-Kutta type of methods in solving the initial value problems.

(iv)MCPI methods can solve two-point boundary value problems computationally efficiently and with high accuracy without requiring shooting methods or gradient information.

3 Simulation Results

3.1 MCPI for1-day attitude integration

Before integrating the coupled orbit-attitude dynamics,we study the performance of MCPI for integrating the attitude-only dynamics.We consider the special case that the body is idealized as axially symmetric and no external torques are present.Notice the only reason we choose this special case is because the solution for this case can be expressed in terms of circular sines and cosines,which provides the baseline to check the accuracy of MCPI as well as to compare MCPI with RK78.The analytical solutions for the angular velocity are[Schaub and Junkins(2009)]:

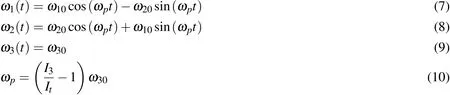
whereω10,ω20,ω30are initial angular velocities andItis the transverse inertia withIt=I1=I2.The solution for the quaternions are solved through Eq.6.

We choose a flat plate with dimension of 1meter by 1meter and AMR equaling one,leading to the mass of the plate as 1kg and the inertia of[1,1,10]kg·m2.The initial angular velocity is chosen asdeg/s and initial quaternion is chosen asSimulation results from using MCPI and RK78 are displayed from Fig.1 to Fig.8.Fig.1 shows that MCPI achieves about four times speedup over RK78 while other figures confirm that this speedup is achieved simultaneously with a superior accuracy.Fig.2 shows that MCPI has two magnitudes of better accuracy than RK78 in maintaining the unity constraint for the quaternions.Fig.3 to Fig.6 compare the angular velocity errors of MCPI and RK78,illustrating that MCPI achieved about four orders of magnitude better accuracy than RK78.Fig.7 and Fig.8 compare the capability of MCPI and RK78 in conserving the Hamiltonian and energy for this torque-free motion.Again,the better accuracy of MCPI is supported by the simulation results.

A special feature of using MCPI for attitude integration in terms of quaternions is that the unity constraint can be conveniently maintained.This normalization is done to provide an improved “warm start”for additional Picard iterations(via MCPI).The normalization only affects the initiation of the MCPI implementation of Picard iteration which is theoretically attracted to the accurate final solution without explicit imposition of the normalization constraint.Suppose the solution at one of the nodes obtained at one iteration is[q1,q2·q3,q4].The normalized solution to start the final convergent Picard iteration is

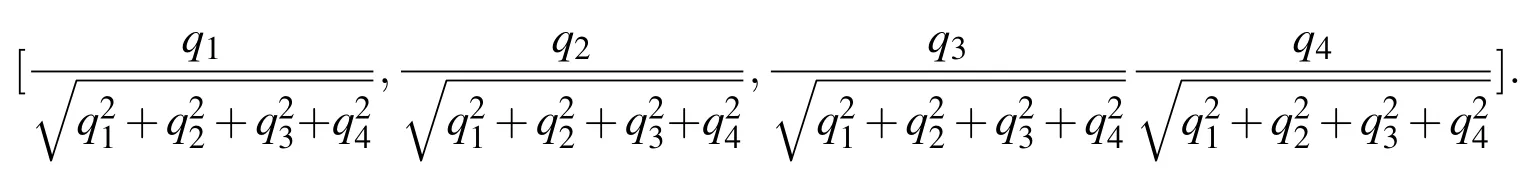
Again,this normalization is“believed”only as an approximation to improve the“warm start”Picard iteration and the final converged iteration does not impose this constraint.We do,however,check the constraint normalization error and other metrics to confirm when the final convergence is achieved.We have invariably found that the final iterations are of near machine precision magnitude and on the tangent plane of the unit sphere constraint surface(essentially correcting the near machine precision errors in the last warm start).

Two approaches can be adopted to realize this. We can either normalize quaternions according to its second norm after each iteration,or we can switch between the normalization iteration and the non-normalization iteration.Fig.9 compares the CPU time using these two approaches. “Approach 1”which normalizes at every iteration takes average 25.6 seconds and “Approach 2”which normalizes at every other iteration takes average 23.6 seconds.This is expected since the normalization can be done simultaneously across all the nodes,thus there is computation saving from the second approach but it is not significant.3.2 illustrates that both approaches can maintain the unity constraint to machine accuracy.Notice the converged iteration is guaranteed to maintain the unity constraint,otherwise we will call a new iteration.We emphasize that this “ad hoc”approach to normalize the quaternion is providing a more physically correct hot start for MCPI which is theoretically attracted to the solution.This will have the consequence of initiating MCPI multiple times from neighboring trajectories which will satisfy the norm=1 constraint at every node to near machine precision.The corrections can be done independently at each node.Furthermore,MCPI makes this process more rigorous than the identical re-scaling when using traditional,e.g.,Runge-Kutta step-by-step integrators,because we follow each re-scale with an unconstrained MCPI correction that is theoretically attracted to the actual solution.The heuristic justification is that we insist that our“hot re-starts”of MCPI near final convergence be from closely-neighboring previous MCPI iterations that satisfies the quaternion norm to machine precision.As Picard iteration theoretically is a contraction mapping to the actual solution of the differential equations,and the quaternion norm is simply an attribute of the exact solution,the final MCPI solution satisfies(to high precision)both the differential equations and also the quaternion constraint.However,the traditional methods obtain the solutions first and then normalize,which evidently does not lead to precise solutions(although the violations are usually very small).

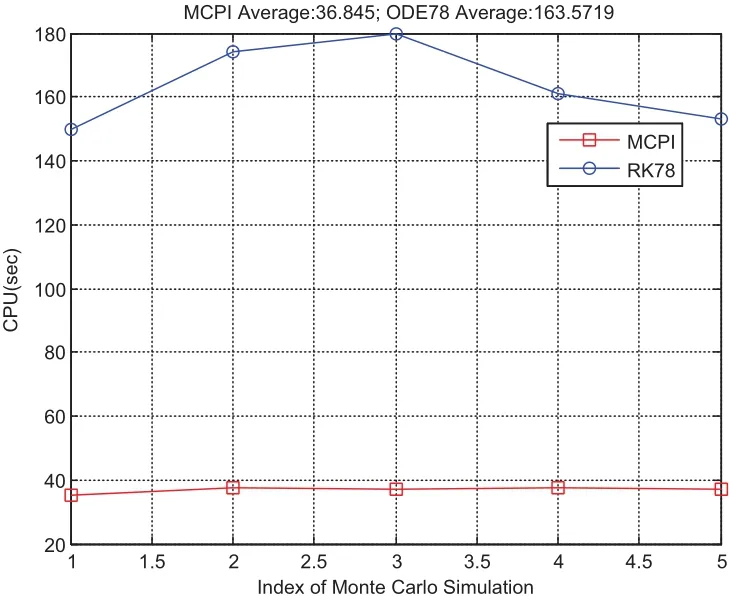
Figure 1:CPU time comparison

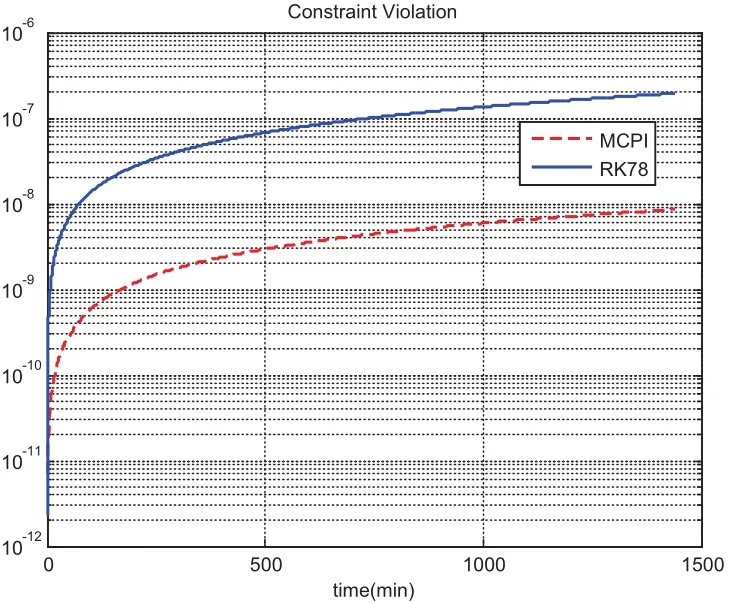
Figure 2:Unity violation comparison

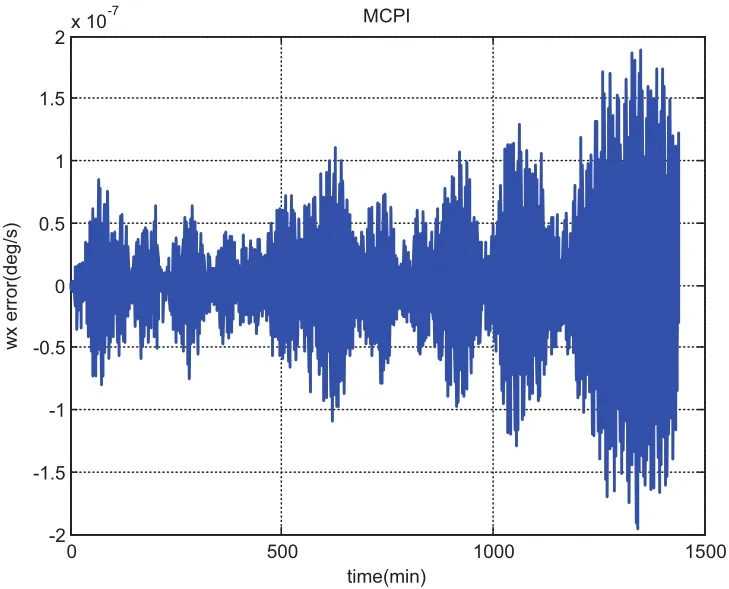
Figure 3:error(MCPI)

Figure 4:error(RK78)

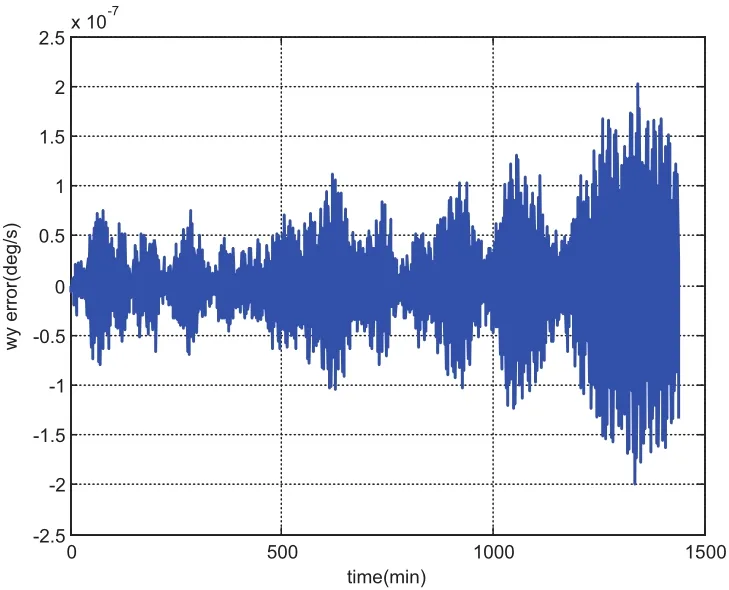
Figure 5:error(MCPI)

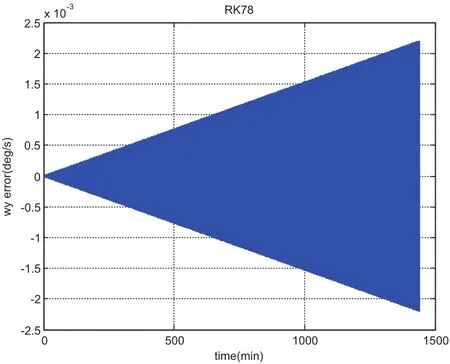
Figure 6:error(RK78)

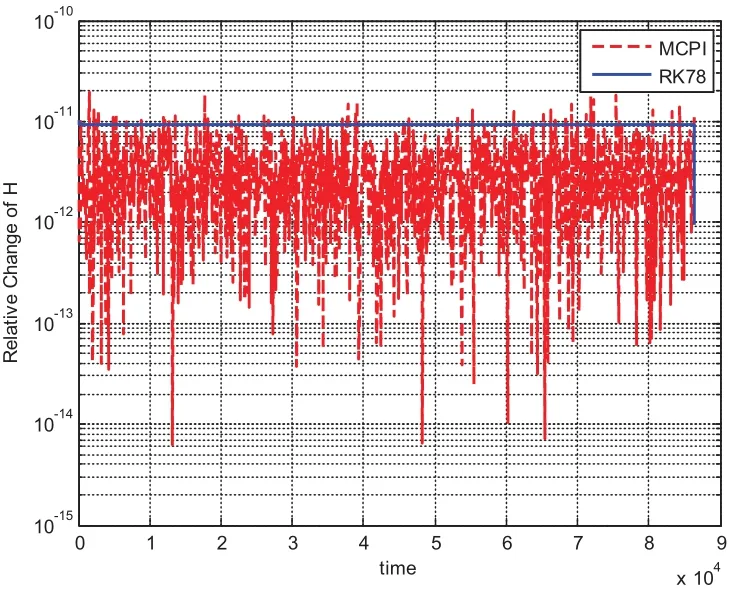
Figure 7: Hamiltonian conservation comparison

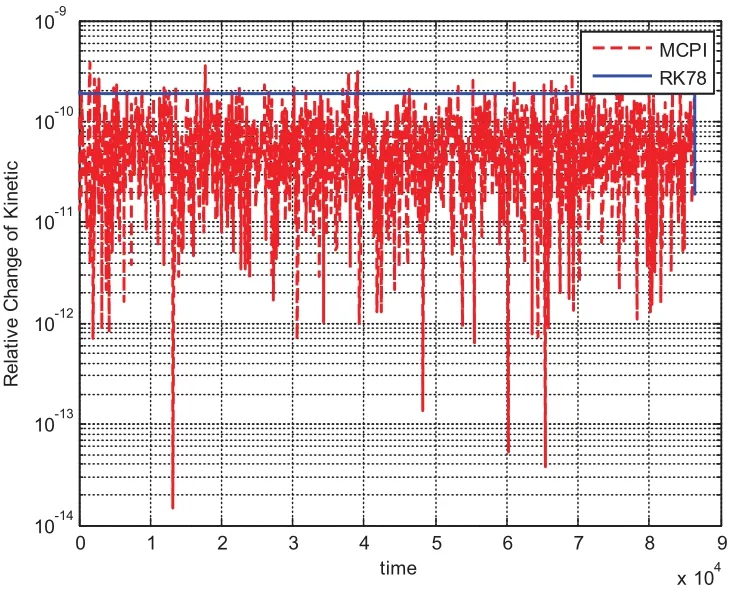
Figure 8:Energy conservation comparison

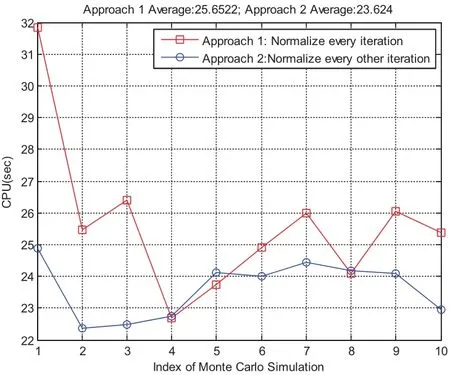
Figure 9:CPU time comparison

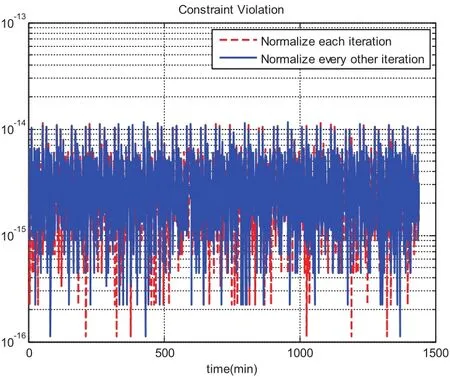
Figure 10:Unity violation comparison(constrained)

3.2 MCPI for coupled orbit-attitude integration

For the coupled orbit-attitude integration,we consider a 10-day integration of a flat plate with dimension of 1meter by 1meter and its AMR equals to one,leading to the mass of the plate as 1kg and the inertia of[1,1,10]kg·m2.This HAMR object is assumed in a geosynchronous orbit with initial positionkm and initial velocityThe initial angular velocity isand quaternionThe specular reflection coefficientCs,i=0.8 and the diffuse reflection coefficientCd,i=0.The epoch is chosen as January 1,2020,00:00:00,at that time the geocentric position of the Sun is calculated.We did not update the Sun’s position as well as not include the Earth shadow effect in this study.Additionally,the perturbation torque by the solar radiation pressure is assumed to be zero,leading to the Hamiltonian of the rotational dynamics be constant thus providing a baseline for accuracy check.Since these assumptions are equally applied to both MCPI and RK78,adding the constraints shall not change the computational comparison results between the two methods.We also emphasize the numerical integration is set up in a general way and other perturbation force and torque can be easily included.

3.2.1Basic MCPI for coupled orbit-attitude integration

For this case,MCPI uses order 40 to approximate both the rotational dynamics and translational dynamics.The segment length is three hours.Fig.11 compares the CPU time required for orbit-only integration which takes an average of 0.1 seconds and the integration for the coupled orbit-attitude case which takes an average of 0.7 seconds.The position deviations with and without SRP effect are shown in Fig.12.Notice without the SRP,the two-body solution along thezaxis will stay zero but will have oscillations with the SRP.Additionally,the effect of SRP leads to about 1000km distance errors thus it is important to be carefully taken into account.Fig.13 compares the CPU time required by using MCPI which takes average 0.7 seconds and by using RK78 which takes average 3 seconds,thus MCPI has a speedup four times over RK78.Fig.14 illustrates that both MCPI and RK78 achieve high accuracy in maintaining the Hamiltonian.The step sizes used by RK78 are shown in its histogram form at Fig.15,and the percentage of these step sizes that are used by RK78 is displayed in Fig.16,illustrating that more than 60%of the step sizes are less than 250 seconds.Comparing with the step size of 3 hours that MCPI uses,the speedup from using MCPI over RK78 is easy to understand.

3.2.2More speedup from MCPI by smart coupling

A special technique that has been developed recently for MCPI is what is called warm-start[Macomber(2015)].The basic idea is that a low accuracy dynamical model can be used at the initial MCPI iterations and the high-accuracy and computationally intensive dynamical models will be used only when the iteration is in the region of its geometric convergence,thus only a few numbers of iterations.Significant computational time can be saved as shown in Macomber’s dissertation[Macomber(2015)].Here we integrate the decoupled orbit dynamics and attitude dynamics initially,and only couple the full dynamics when the attitude solution is converging.A tuning process is required for this approach,through which we find the threshold to couple the orbital integration and attitude integration with sufficient accuracy for the current demonstration.Notice a poor threshold could lead to instability of the iterations.

Fig.17 compares the CPU time when using the basic MCPI as well as this warmstart approach.The relative time saving shown in Fig.18 illustrates this saving can be as high as 10%.The position and velocity difference for these two approaches are displayed in Fig.19 and Fig.20.The position difference is in the range of centimeter and the velocity difference is in the range of 10?3milimeter/seconds,which confirms that the speedup from using this warm-start approach is achieved without losing accuracy.

We emphasize that the final solutions from MCPI through this smart preliminary coupling approach are accurate solution of the fully coupled dynamics that again enjoy the theoretical attraction to the exact solution of Picard iteration operating on the fully coupled differential equations.This is different from other traditional methods that decouples the dynamics first and then couples the dynamics to make corrections on the decoupled solutions,and most importantly,these methods utilize algorithms without a theoretical convergence guarantee.Since the approximate coupling phase usually does not solve the original differential equations,the solutions from these types of methods can be expected to have less accuracy than the final Picard iteration solutions of the fully coupled differential equations from the MCPI methods proposed in this paper.

3.2.3Further speedup by reducing the position tolerance

If we loosen the accuracy requirement,more speedup could be achieved.Fig.21 compares the CPU time when using the basic MCPI as well as the warm-start approach but with a low accuracy requirement.The relative time saving shown in Fig.22 illustrates this saving can be as high as 16%.Fig.23 and Fig.24 show the position errors are in the range of 10km and the velocity errors are in the range of 10?4km/s.

Finally,we summarize the CPU times for the four cases we have discussed in Fig.25.The relative time savings using three types of MCPI over RK78 are displayed in Fig.26,thus MCPI methods save 70–80%of CPU time over RK78.We re-emphasize,because MCPI is highly parallelizable and the Runge-Kutta methods are not,further orders of magnitude speedup is conveniently achievable if,for example,we are doing a Monte-Carlo study to accommodate uncertainty considerations.Furthermore,for Monte-Carlo studies,typically the nominal converged 6 DOF orbit and attitude solution can “warm start”all of the Monte-Carlo trajectories.The individual Monte-Carlo trials can be computed in parallel,and with MCPI,each state history propagation is itself parallelizable,therefore massive parallelizable Monte-Carlo studies are possible with the details depending on the machine architecture.

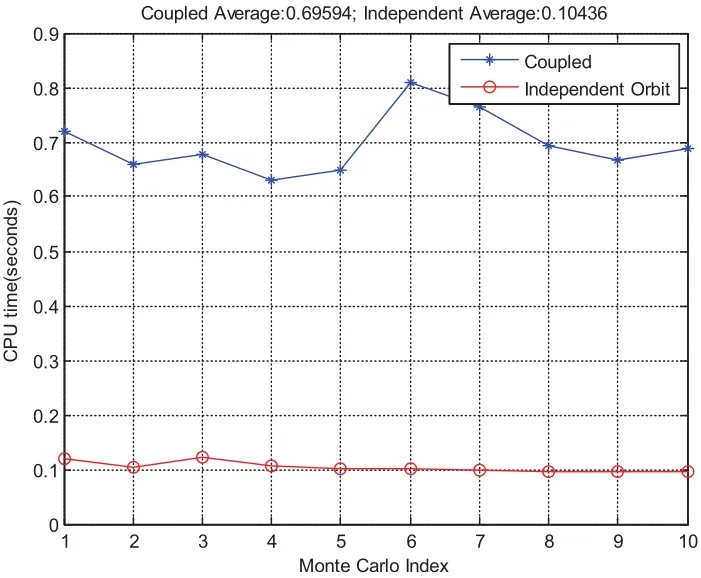
Figure 11:CPU time comparison

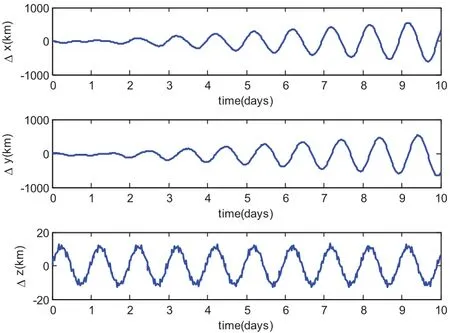
Figure 12:Position deviation from 2-body solution:w/and w/o SRP

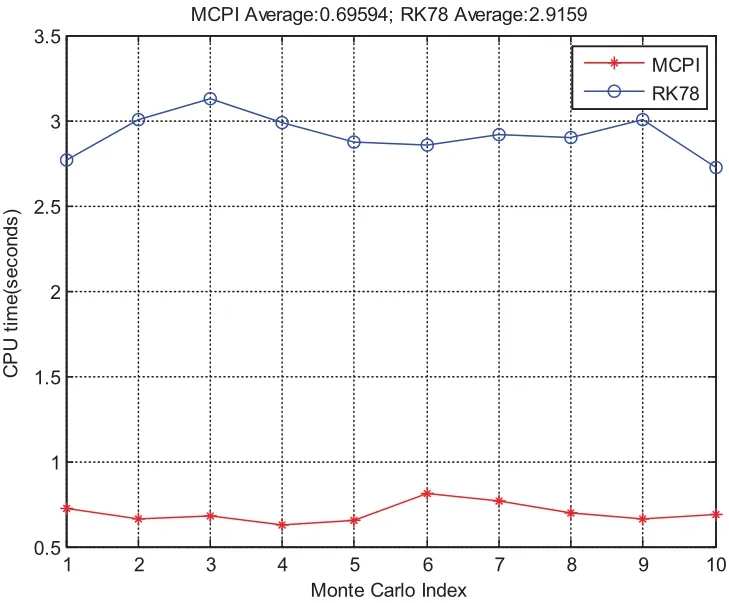
Figure 13:CPU time(MCPI&RK78)

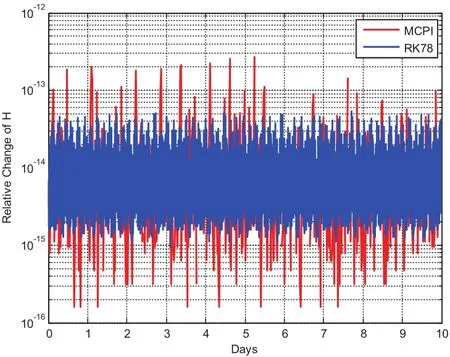
Figure 14: Hamiltonian (MCPI&RK78)

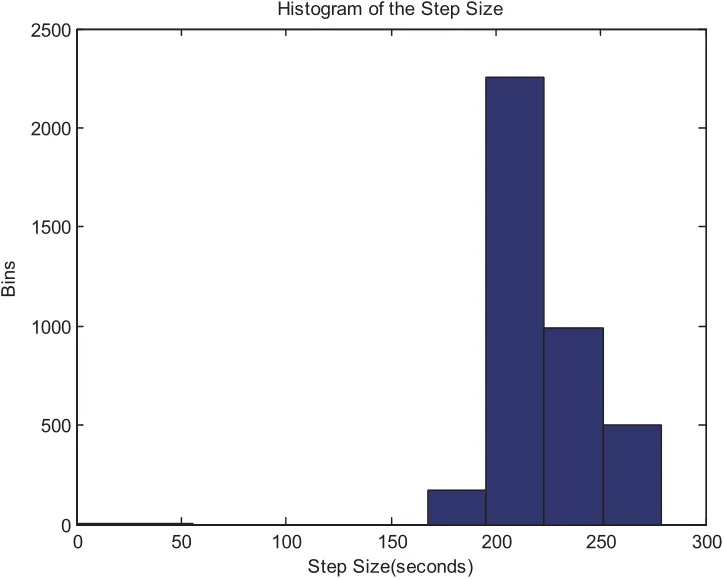
Figure 15: Histogram of step size:RK78

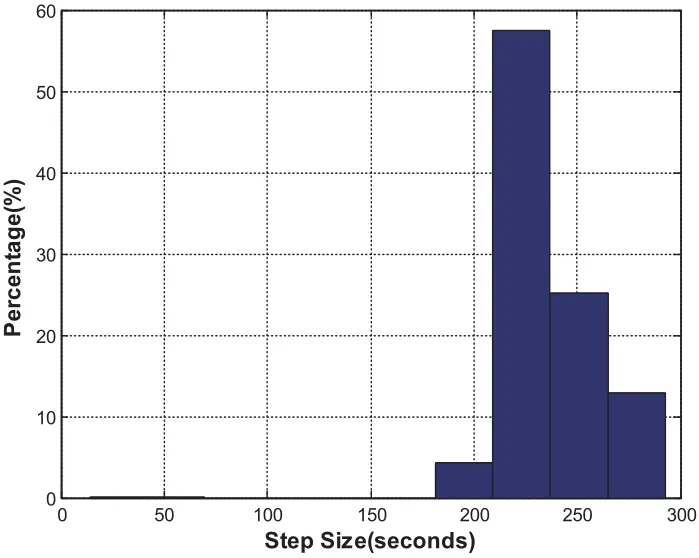
Figure 16: Percentage of step size:RK78

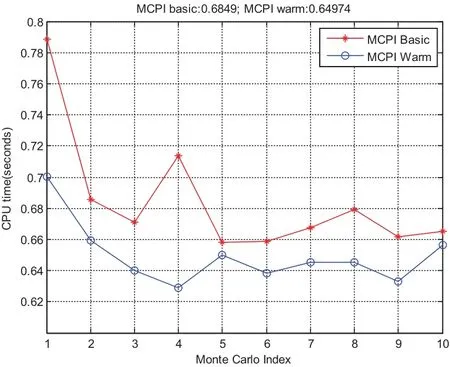
Figure 17:CPU time comparison

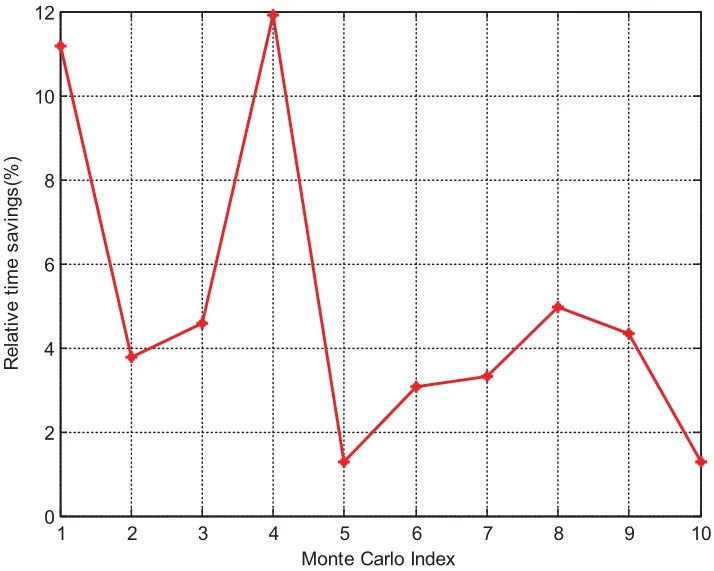
Figure 18:Relative time saving

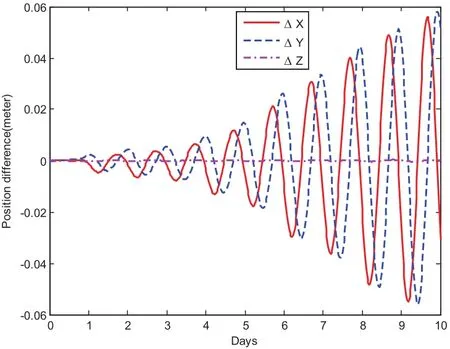
Figure 19:Position difference

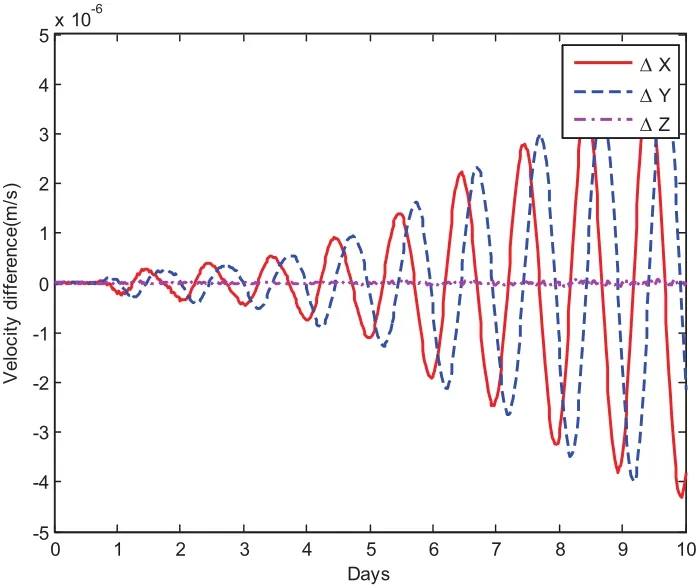
Figure 20:Velocity difference

Figure 21:CPU time comparison

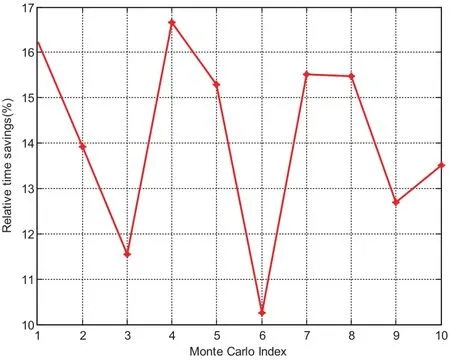
Figure 22:Relative time saving

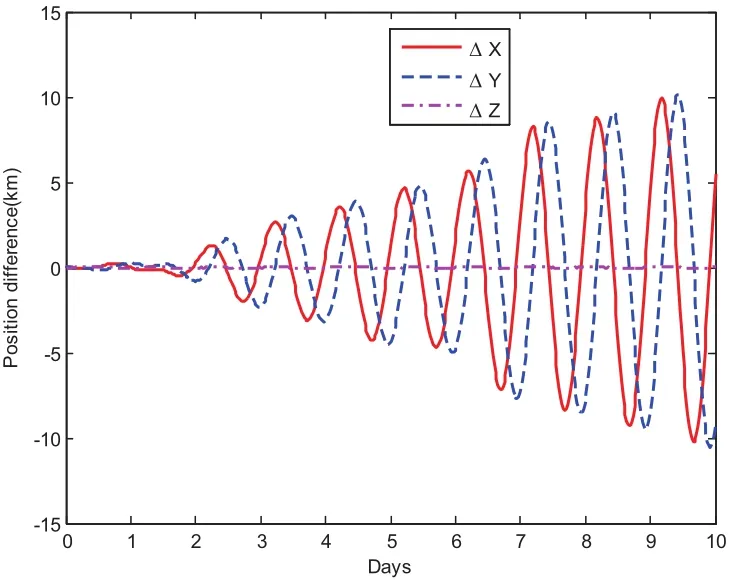
Figure 23:Position difference

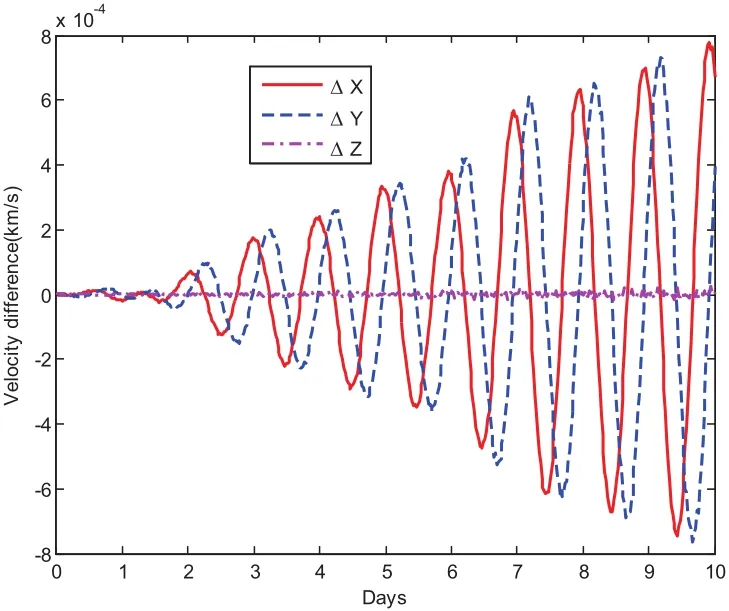
Figure 24:Velocity difference

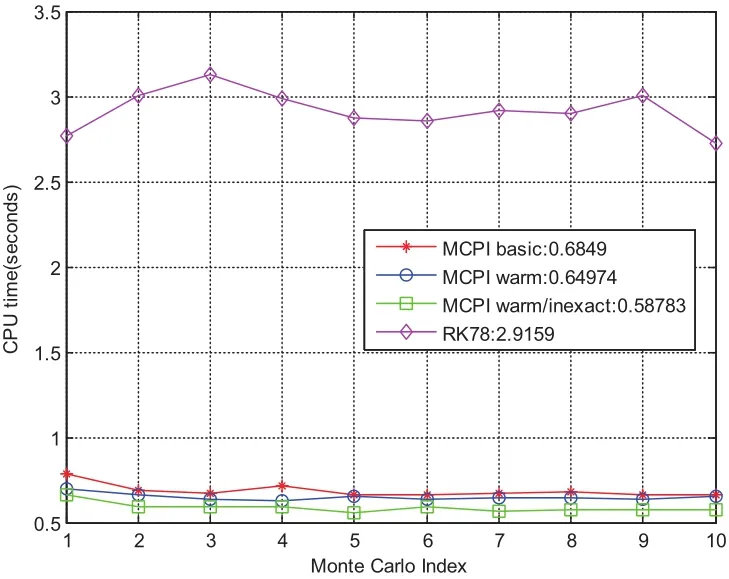
Figure 25:CPU time comparison

Figure 26:Relative time savings

4 Conclusions

This paper assesses the capability of Modified Chebyshev-Picard Iteration(MCPI)methods for coupled orbit-attitude integration.The performance of MCPI in integrating the rotational dynamics is first reported through integrating a torque-free rotation,where MCPI achieves four times of speedup over Runge-Kutta methods using Dormand and Prince’s 8–7th order formulas(RK78)with four magnitude better accuracy.For the coupled orbit-attitude case,a 10-day integration of a HAMR object in geosynchronous orbit is studied and the computational advantage to use MCPI is demonstrated:the basic MCPI is shown to save CPU time about 70%over RK78;using the warm start approach through which the orbit dynamics and attitude dynamics are integrated separately initially,but are coupled when the attitude dynamics is converging,the time savings can be as high as 80%;and further speedup is achieved if the accuracy requirement is in the range of kilometer.

Since earlier studies have proven that the MCPI methods are more computationally efficient than other Runge-Kutta type of methods for orbit propagation,“the computational savings through using MCPI for the fully coupled dynamics are expected and should be augmented in future studies with a wider class of force models and orbit/attitude motions”.Additionally,parallelization will lead to orders of magnitude of additional speedup,due to the inherent parallel structure of MCPI.Since the performance of MCPI is dependent on both the parallel processors and the equations to solve,significant research and expertise on both the hardware and software are required for a solid demonstration.The authors have been researching on this aspect and are making progress and anticipate parallel implementation performance will be reported in the near future.

Schildknecht,T.;Musci,R.;Ploner,M.;Beutler,G.;Flury,W.;Kuusela,J.;Cruz Palmero,L.D.F.D.(2004):Optical observations of space debris in GEO and in highly-eccentric orbits.Advances in Space Research,vol.34,no.5,pp.901–911.

Schildknecht,T.;Musci,R.;Ploner,M.;Flury,W.;Kuusela,J.;de León Cruz,J.;de Fatima Domínguez Palmero,L.(2003):An optical search for small-size debris in GEO and GTO.In Proceedings of the 2003 AMOS Technical Conference.

Anselmo,L.;Pardini,C.(2010):Long-term dynamical evolution of high area-tomass ratio debris released into high earth orbits.Acta Astronautica,vol.67,no.1,pp.204–216.

Pardini,C.;Anselmo,L.(2009):Assessment of the consequences of the Fengyun-1C breakup in low earth orbit.Advances in Space Research,vol.44,no.5,pp.545–557.

Woodburn,J.(2001):Efficient numerical integration of coupled orbit and attitude trajectories using an encke type correction algorithm.AAS 01-428,AAS/AIAA Astrodynamics Specialist Conference,Quebec City,Canada,2001.

Früh,C.;Kelecy,T.M.;Jah,M.K.(2013):Coupled orbit-attitude dynamics of high area-to-mass ratio(HAMR)objects:influence of solar radiation pressure,Earth’s shadow and the visibility in light curves.Celestial Mechanics and Dynamical Astronomy,vol.117,no.4,pp.385–404.

Bai,X.(2010):Modified Chebyshev-Picard Iteration Methods for Solution of Initial Value and Boundary Value Problems.Ph.D.Dissertation,Texas A&M University,College Station,TX.

Bai,X.;Junkins,J.L.(2011):Modified chebyshev-picard iteration methods for orbit propagation.The Journal of the Astronautical Sciences,vol.58,no.4,pp.583–613.

Bai,X.;Junkins,J.L.(2011):Modified Chebyshev-Picard iteration methods for solution of boundary value problems.The Journal of the Astronautical Sciences,vol.58,no.4,pp.615–642.

Younes,A.B.;(2013):Orthogonal polynomial approximation in higher dimensions:Applications in astrodynamics,Ph.D.Dissertation,Texas A&M University,College Station,TX.

Macomber,B.(2015):Enhancements of Chebyshev Picard Iteration Efficiency for Generally Perturbed Orbits and Constrained Dynamical Systems,Ph.D.Dissertation,Texas A&M University,College Station,TX.

Nielsen,P.D.;Alfriend,K.T.;Bloomfield,M.J.;Emmert,J.T.;Guo,Y.;Maclay,T.D.M.;Saari,D.G.(2012):Continuing Kepler’s Quest:Assessing Air Force Space Command’s Astrodynamics Standards.Technical Report,National Research Council.

Prince,P.J.;Dormand,J.R.(1981):High order embedded Runge-Kutta formulae.Journal of Computational and Applied Mathematics,vol.7,no.1,pp.67–75.

Fahnestock,E.G.;Lee,T.;Leok,M.;McClamroch,N.H.;Scheeres,D.J.(2006):Polyhedral potential and variational integrator computation of the full two body problem.In Proc.AIAA/AAS Astrodynamics Specialist Conf.;AIAA-2006-6289.

Park,H.E.;Park,S.Y.;Park,C.;Kim,S.W.(2013):Development of integrated orbit and attitude software-in-the-loop simulator for satellite formation flying.Journal of Astronomy and Space Sciences,vol.30,pp.1–10.

Schaub,H.;Junkins,J.L.(2009):Analytical mechanics of space systems.Second Edition,American Institute of Aeronautics&Astronautics.

Altman,S.P.(1972):A unified state model of orbital trajectory and attitude dynamics.Celestial mechanics,vol.6,no.4,pp.425–446.

Altman,S.P.(1975):Velocity-space maps and transforms of tracking observations for orbital trajectory state analysis.Celestial Mechanics,vol.11,no.4,pp.405–428.

Raol,J.R.;Sinha,N.K.(1985):On the orbit determination problem.Aerospace and Electronic Systems,IEEE Transactions on,vol.3,pp.274–291.

Vittaldev,V.;Mooij,E.;Naeije,M.C.(2012):Unified state model theory and application in astrodynamics.Celestial Mechanics and Dynamical Astronomy,vol.112,no.3,pp.253–282.

Shuster,M.D.(1993):A survey of attitude representations.Navigation,vol.8,no.9,pp.439–517.

1Rutgers,The State University of New Jersey,Piscataway,NJ,U.S.A

2Texas A&M,College Station,TX,U.S.A