HE Guo-qing

(School of Mathematics and Computer Science,Anhui Normal University,Wuhu 241000,China)

CHEN-RICCI INEQUALITIES FOR SUBMANIFOLDS OF GENERALIZED COMPLEX SPACE FORMS WITH SEMI-SYMMETRIC METRIC CONNECTIONS

HE Guo-qing

(School of Mathematics and Computer Science,Anhui Normal University,Wuhu 241000,China)

In this paper,we study Chen-Ricci inequalities for submanifolds of generalized complex space forms endowed with a semi-symmetric metric connection.By using algebraic techniques,we establish Chen-Ricci inequalities between the mean curvature associated with a semisymmetric metric connection and certain intrinsic invariants involving the Ricci curvature and k-Ricci curvature of submanifolds,which generalize some of Mihai andzgr’s results.

Chen-Ricci inequality;k-Ricci curvature;generalized complex space form;semisymmetric metric connection

2010 MR Subject Classification:53C40

Document code:AArticle ID:0255-7797(2016)06-1133-09

1　Introduction

Since the celebrated theory of Nash[1]of isometric immersion of a Riemannian manifold into a suitable Euclidean space gave very important and effective motivation to view each Riemannian manifold as a submanifold in a Euclidean space,the problem of discovering simple sharp relationships between intrinsic and extrinsic invariants of a Riemannian submanifold becomes one of the most fundamental problems in submanifold theory.The main extrinsic invariant of a submanifold is the squared mean curvature and the main intrinsic invariants of a manifold include the Ricci curvature and the scalar curvature.There were also many other important modern intrinsic invariants of(sub)manifolds introduced by Chen such as k-Ricci curvature(see[2-4]).

In 1999,Chen[5]proved a basic inequality involving the Ricci curvature and the squared mean curvature of submanifolds in a real space form Rm(C).This inequality is now called Chen-Ricci inequality[6].In[5],Chen also defined the k-Ricci curvature of a k-plane section of TxMn,x∈M,where Mnis a submanifold of the real space form Rn+p(C).And he proved a basic inequality involving the k-Ricci curvature and the squared mean curvature of the submanifold Mn.These inequalities described relationships between the intrinsicinvariants and the extrinsic invariants of a Riemannian submanifold and drew attentions of many people.Similar inequalities are studied for different submanifolds in various ambient manifolds(see[7-10]).

On the other hand,Hayden[11]introduced a notion of a semi-symmetric connection on a Riemannian manifold.Yano[12]studied Riemannaian manifolds endowed with a semisymmetric connection.Nakao[13]studied submanifolds of Riemannian manifolds with a semi-symmetric metric connection.Recently,Mihai andzgr[14,15]studied Chen inequalities for submanifolds of real space forms admitting a semi-symmetric metric connection and Chen inequalities for submanifolds of complex space forms and Sasakian space forms with a semi-symmetric metric connection,respectively.Motivated by studies of the above authors,in this paper we establish Chen-Ricci inequalities for submanifolds in generalized complex forms with a semi-symmetric metric connection.

2　Preliminaries

Let Nn+pbe an(n+p)-dimensional Riemannian manifold with Riemannian metric g and a linear connectionon Nn+p.If the torsion tensordefined by

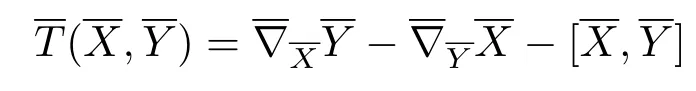
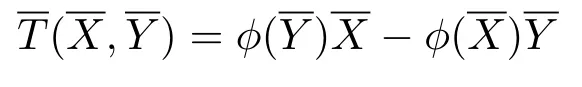
for a 1-form φ,then the connectionis called a semi-symmetric connection.Furthermore, ifsatisfies=0,thenis called a semi-symmetric metric connection.Letdenote the Levi-Civita connection with respect to the Riemannian metric g.In[12]Yano gave a semi-symmetric metric connectionwhich can be written as

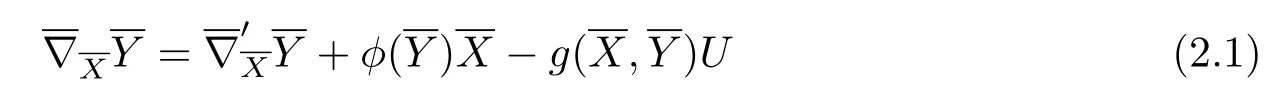
Let Mnbe an n-dimensional submanifold of Nn+pwith a semi-symmetric metric connectionand the Levi-Civita connection.On the submanifold Mnwe consider the induced semi-symmetric metric connection denoted by?and the induced Levi-Civita connection denoted by?＇.The Gauss formulas with respect to?and?＇,respectively,can be written as

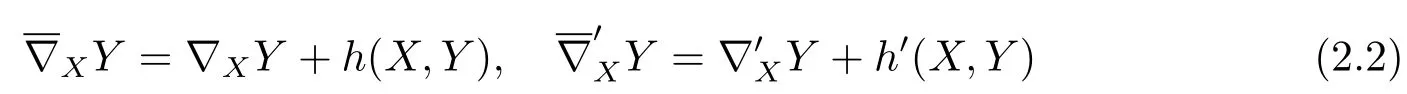
for any vector fields X,Y on Mn,where h＇is the second fundamental form of Mnin Nn+pand h is a(0,2)-tensor on Mn.According to formula(7)in[13],h is also symmetric.

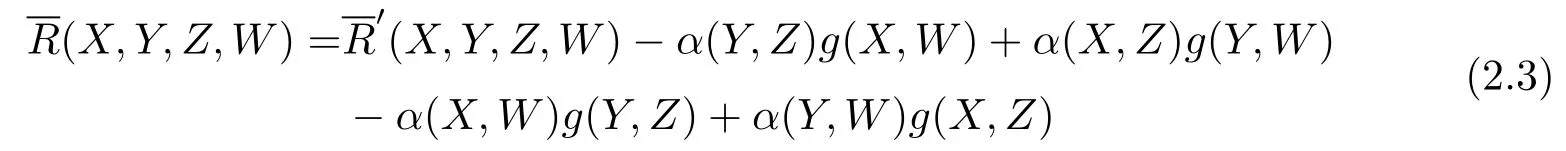
for any vector fields X,Y,Z,Won Mn,where α is a(0,2)-tensor field defined by

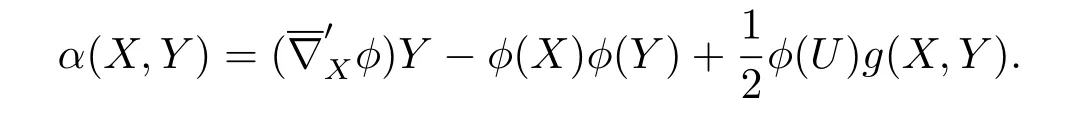
Denote by λ the trace of α.The Gauss equation for the submanifold Mnin Nn+pis

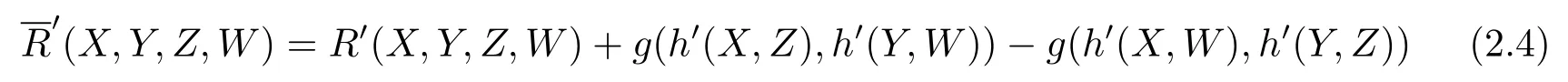
for any vector fields X,Y,Z,Won Mn.In[13],the Gauss equation with respect to the semi-symmetric metric connection is

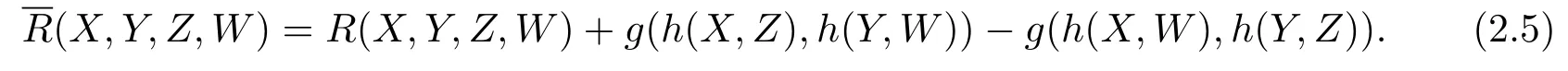
In Nn+pwe can choose a local orthonormal frame{e1,···,en,en+1,···,en+p}such that restricting to Mn,e1,···,enare tangent to Mn.Setting=g(h(ei,ej),er),then the squared length of h is

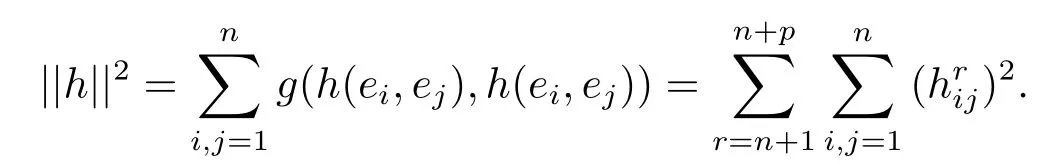
The mean curvature vector of Mnassociated toh(ei,ei)and the mean curvature vector of Mnassociated to

Let π?TxMnbe a 2-plane section for any x∈Mnand K(π)be the sectional curvature of π associated to the induced semi-symmetric metric connection?.The scalar curvature τ at x with respect to?is defined by

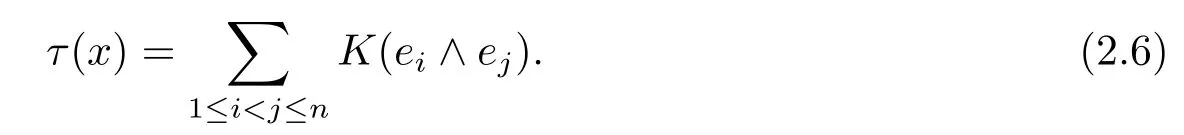
The following lemmas will be used in the paper.

Lemma 2.1(see[13])If U is a tangent vector field on Mn,we have H=H＇,h=h＇.

Lemma 2.2(see[13])Let Mnbe an n-dimensional submanifold of an(n+p)-dimensional Riemannian manifold Nn+pwith the semi-symmetric metric connectionThen

(i)Mnis totally geodesic with respect to the Levi-Civita connection and with respect to the semi-symmetric metric connection if and only if U is tangent to Mn.

(ii)Mnis totally umbilical with respect to the Levi-Civita connection if and only if Mnis totally umbilical with respect to the semi-symmetric metric connection.

Lemma 2.3(see[10])Let f(x1,x2,···,xn)be a function on Rndefined by

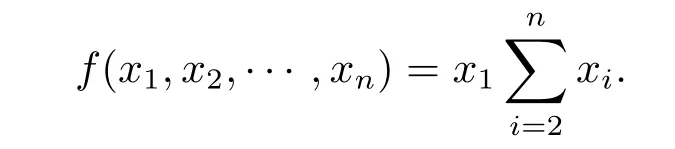
If x1+x2+···+xn=2ε,then we have

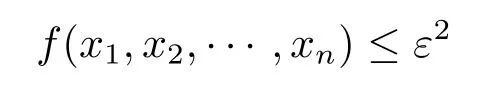
with the equality holding if and only if x1=x2+xn+···+xn=ε.

A 2m-dimensional almost Hermitian manifold(N,J,g)is said to be a generalized complex space form(see[16,17])if there exists two functions F1and F2on N such that

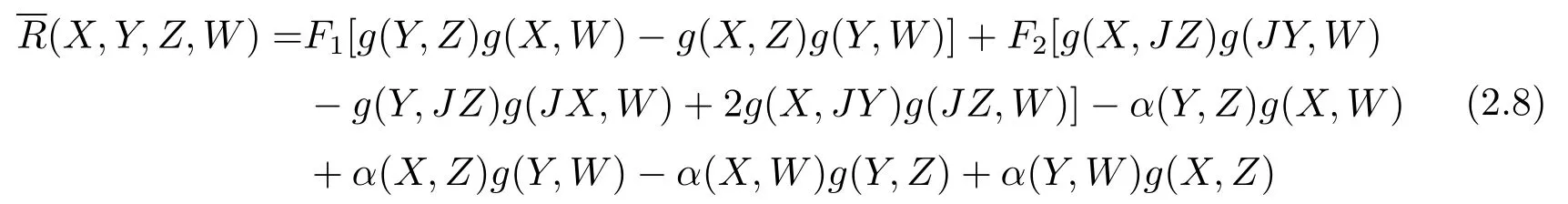
for X,Y,Z,W on M,where M is a submanifold of N.

Let M be an n-dimensional submanifold of a 2m-dimensional generalized complex space form N(F1,F2).We set JX=PX+FX for any vector field X tangent to M,where PX and FX are tangential and normal components of JX,respectively.

3　Chen-Ricci Inequality

In this section,we establish a sharp relation between the Ricci curvature along the direction of an unit tangent vector X and the mean curvature||H||with respect to the semi-symmetric metric connect

Theorem 3.1 Let Mn,n≥2,be an n-dimensional submanifold of a 2m-dimensional generalized complex space form N(F1,F2)endowed with the semi-symmetric metric connectionFor each unit vector X∈TxM,we have

(1)

(2)If H(x)=0,then a unit tangent vector X at x satisfies the equality case of(3.1)if and only if X∈N(x)={X∈TxM:h(X,Y)=0,?Y∈TxM}.

(3)The equality of inequality(3.1)holds identically for all unit tangent vectors at x if and only if in the case of n=0,i,j=1,2···,n;r=n+1,···,2m,or in the case of n=2,

Proof (1)Let X∈TxM be an unit tangent vector at x.We choose an orthonormal basis e1,···,en,en+1···,e2msuch that e1,···,enare tangent to M at x and e1=X.

When we set X=W=ei,Y=Z=ej,i,j=1,···,n,ij in(2.5)and(2.8),we have

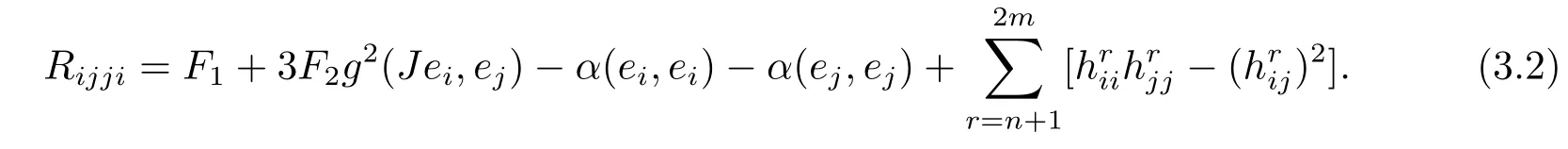
Using(3.2),we get

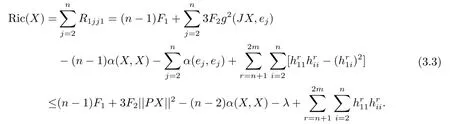
We consider the maximum of the function

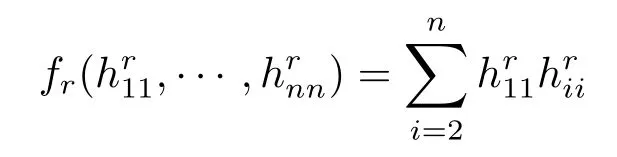
From Lemma 2.3 we know the solution()of this problem must satisfy

So it follows that

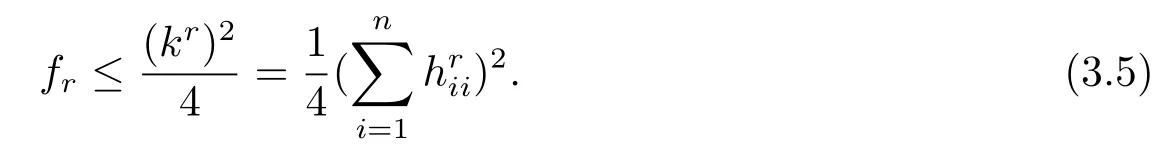
From(3.3)and(3.5)we have

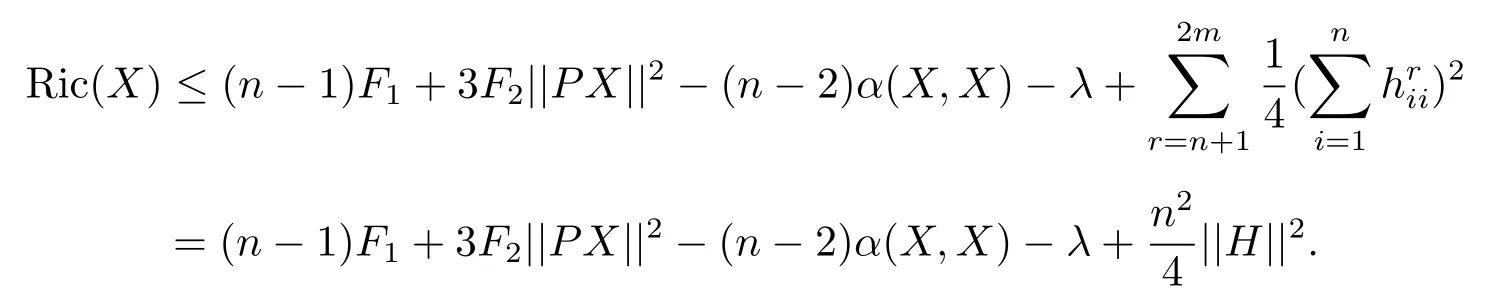
(2)For the unit vector X at x,if the equality case of inequality(3.1)holds,using(3.3), (3.4)and(3.5)we have

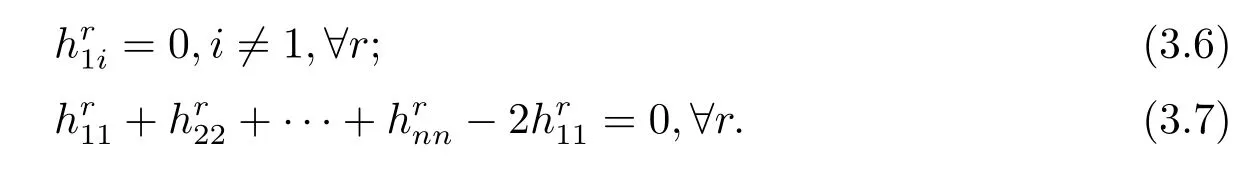
The converse is obvious.

(3)For all unit vector X at x,the equality case of inequality(3.1)holds.Let X= ei,i=1,2···n,as in(2),we have

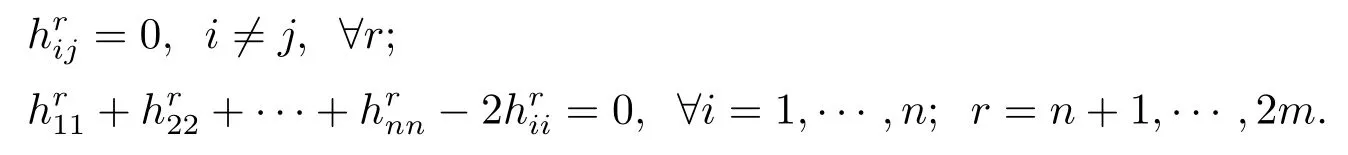
We can distinguish two cases:

(b)in the case of n=2,we have

The converse is trivial.

Corollary 3.2 If the equality case of inequality(3.1)holds for all unit tangent vector X of Mn,then we have

(1)the equality case of inequality(3.1)holds for all unit tangent vector X of Mnif and only if Mnis a totally umbilical submanifold;

(2)if U is a tangent field on Mnand n≥3,Mnis a totally geodesic submanifold.

Proof (1)For n=2,from Theorem 3.1 we know the equality case of inequality(3.1) holds for all unit tangent vector X of M2if and only if M2is a totally umbilical submanifold with respect to the semi-symmetric metric connection.Then from Lemma 2.2,M2is a totally umbilical submanifold with respect to the Levi-Civita connection.

For n≥3,from Theorem 3.1 we know the equality case of inequality(3.1)holds for all unit tangent vector X of Mnif and only=0,?i,j,r.According to formula(7)from [13],we have+krgij,where krare real-valued functions on M.Thus we have=krgij.So Mnis a totally umbilical submanifold.

(2)If U is a tangent vector field on Mn,from Lemma 2.1 we have h＇=h.For n≥3, from Theorem 3.1 the equality case of inequality(3.1)holds for all unit tangent vector X of Mnif and only if=0,?i,j,r.Thus we have=0,?i,j,r.So Mnis a totally geodesic submanifold.

4　k-Ricci Curvature

In this section,we establish a sharp relation between the k-Ricci curvature and the mean curvature||H||with respect to the semi-symmetric metric connect

Let L be a k-plane section of TxMn,x∈Mn,and X be a unit vector in L.We choose an orthonormal frame e1,···,ekof L such that e1=X.In[5]the k-Ricci curvature of L at X is defined by

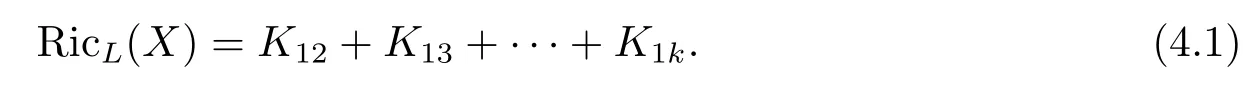
The scalar curvature of a k-plane section L is given by

For an integer k,2≤k≤n,the Riemannian invariant Θkon Mnat x∈Mndefined by

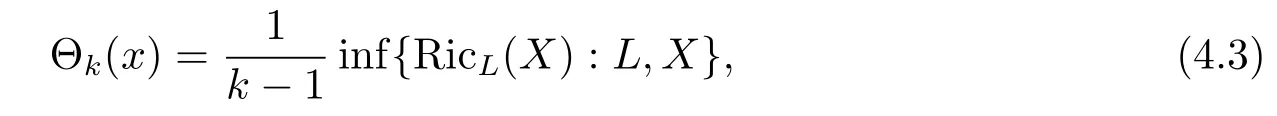
where L runs over all k-plane sections in TxM and X runs over all unit vectors in L.From (2.6),(4.1)and(4.2)for any k-plane section Li1···ikspanned by{ei1,···,eik},it follows that

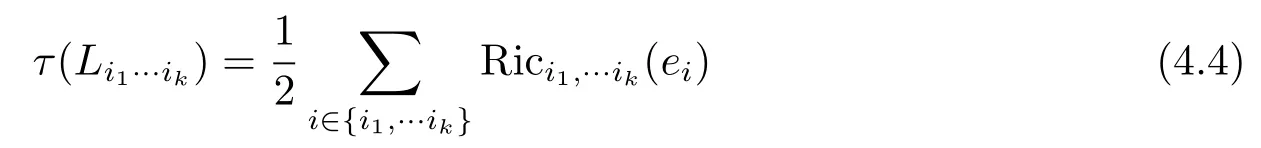
and

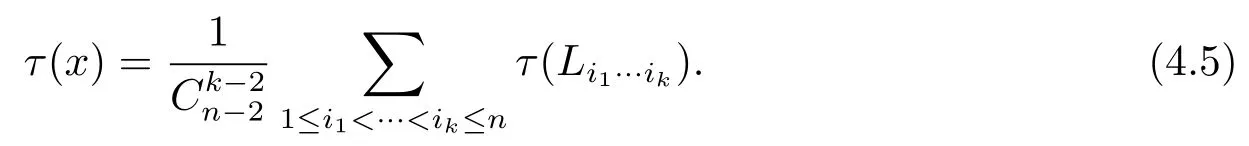
From(4.3),(4.4)and(4.5),we have

Theorem 4.1 Let Mn,n≥3,be an n-dimensional submanifold of a 2m-dimensional generalized complex space form N(F1,F2)endowed with a semi-symmetric connectionThen we have

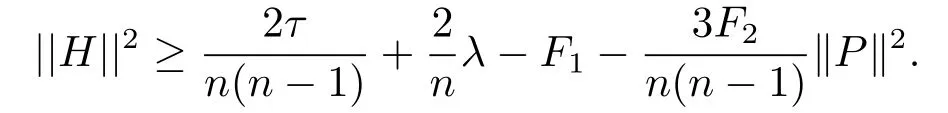
Proof For x∈Mn,let{e1,···,en}and{en+1,···,e2m}be an orthonormal basis ofandM,respectively,where en+1is parallel to the mean curvature vector H.

From(3.2),we have

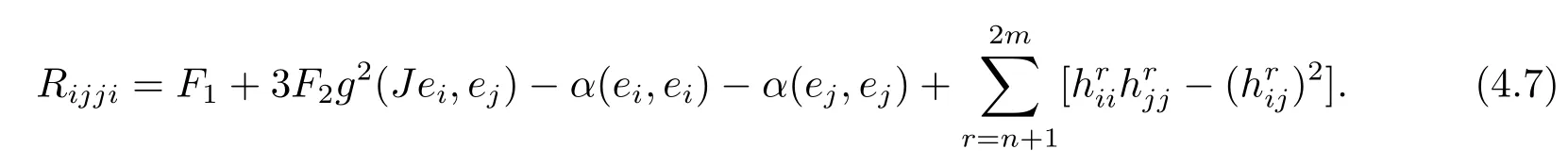
Setting||P||2=(Jei,ej).From(2.6),it follows that

Then equation(4.8)can be also written as

We choose an orthonormal basis{e1,···,en,en+1,···,e2m}such that e1,···,endiagonalize the shape operator Aen+1,i.e.,

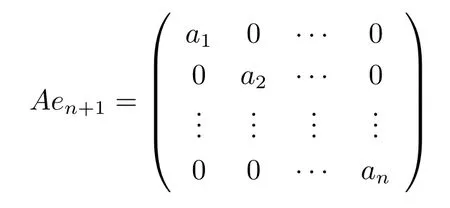
and Aer=(),i,j=1······n;r=n+2,···,2m,traceAer=0.So(4.9)turns into

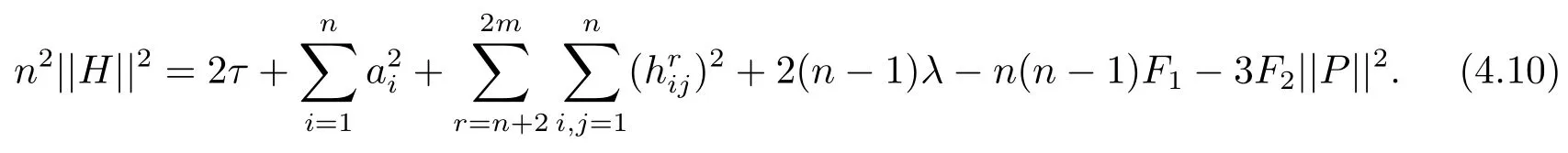
On the other hand,we get

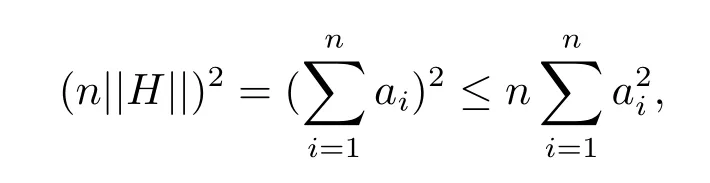
which implies

From(4.10)and(4.11),it follows that

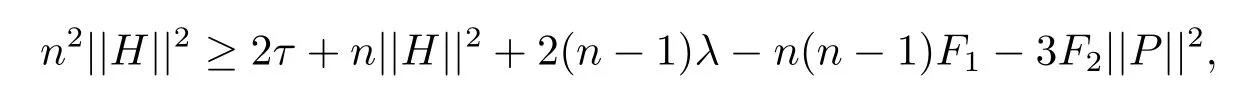
which means

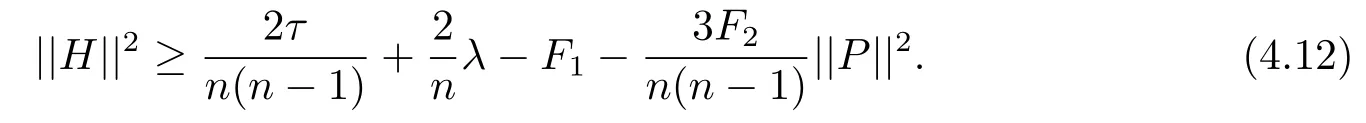
Using Theorem 4.1 and(4.6)we can obtain the following theorem.

Theorem 4.2 Let Mn,n≥3,be an n-dimensional submanifold of a 2m-dimensional generalized complex space form N(F1,F2)endowed with a semi-symmetric connectionThen for any integer k,2≤k≤n,and for any point x∈M,we have

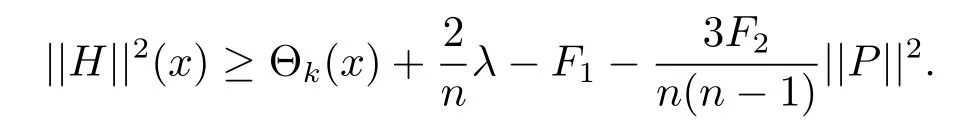
Proof Let{e1,···,en}be an orthonormal basis of TxMnat x∈Mn.The k-plane section spanned by ei1,···,eikis denoted by Li1···ik.

Then from(4.6)and(4.12),we have

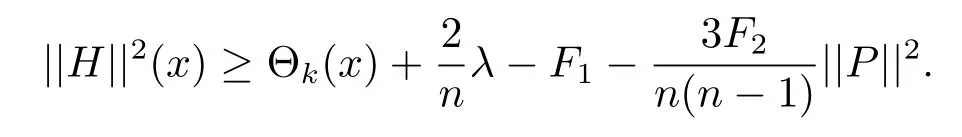
Remark 4.3 For F1=F2=C(C is constant)in Theorem 3.1,we obtain a Chen-Ricci inequality for submanifolds of complex space forms with a semi-symmetric metric connection.

For F1=F2=C(C is constant)in Theorem 4.1 and Theorem 4.2,the results can be found in[15].

References

[1]Nash J F.The imbedding problem for Riemannian manifolds[J].Ann.Math.,1956,63:20-63.

[2]Chen B Y.Some pinching and classification theorems for minimal submanifolds[J].Arch.Math. (Basel),1993,60(6):568-578.

[3]Chen B Y.Strings of Riemannian invariants,inequalities,ideal immersions and their applications[J]. Third Pacific Rim Geom.Conf.(Seoul),1996:7-60.

[4]Chen B Y.Riemannian submanifolds[M].North-Holland,Amsterdam:Handbook Diff.Geom.,2000, 1:187-418.

[5]Chen B Y.Relations between Ricci curvature and shape operator for submanifolds with arbitrary codimensions[J].Glasg.Math.J.,1999,41(1):33-41.

[6]Tripathi M M.Chen-Ricci inequality for submanifolds of contact metric manifolds[J].J.Adv.Math. Studies,2008,1(1-2):111-135.

[7]Chen B Y.On Ricci curvature of isotropic and Lagrangian submanifolds in complex space forms[J]. Arch.Math.(Basel),2000,74:154-160.

[8]Matsumoto K,Mihai I,Oiaga A.Ricci curvature of submanifolds in complex space forms[J].Rev. Roumaine Math.Pures Appl.,2001,46:775-782.

[9]Mihai I.Ricci curvature of submanifolds in Sasakian space forms[J].J.Aust.Math.Soc.,2002, 72(2):247-256.

[10]Zhang Pan,Zhang Liang,Song Wei-dong.Some remarks on geometric inequalities for submanifolds of a riemannian manifold of quasi-constant curvature[J].J.Math.,2016,36(3):445-457.

[11]Haydan H A.Subspaces of a space with torsion[J].Proc.London Math.Soc.,1932,34:27-50.

[12]Yano K.On semi-symmetric metric connection[J].Rev.Roumaine Math.Pures Appl.,1970,15: 1579-1586.

[13]Nakao Z.Submanifolds of a Riemanian with semi-symmetric metric connections[J].Proc.Amer. Math.Soc.,1976,54:261-266.

[16]Tricerri F,Vanhecke L.Curvature tensors on almost Hermitian manifolds[J].Trans.Amer.Math. Soc.,1981,267(2):365-397.

[17]Vanhecke L.Almost Hermitian manifolds with J-invariant Riemann curvature tensor[J].Rend.Sem. Mat.Univ.Politec.Torino,1975,34:487-498.

容有半對(duì)稱度量聯(lián)絡(luò)的廣義復(fù)空間中子流形上的Chen-Ricci不等式

何國(guó)慶

(安徽師范大學(xué)數(shù)學(xué)計(jì)算機(jī)科學(xué)學(xué)院,安徽蕪湖241000)

本文研究了容有半對(duì)稱度量聯(lián)絡(luò)的廣義復(fù)空間中的子流形上的Chen-Ricci不等式.利用代數(shù)技巧,建立了子流形上的Chen-Ricci不等式.這些不等式給出了子流形的外在幾何量―關(guān)于半對(duì)稱聯(lián)絡(luò)的平均曲率與內(nèi)在幾何量―Ricci曲率及k-Ricci曲率之間的關(guān)系,推廣了Mihai和zgr的一些結(jié)果.

Chen-Ricci不等式;k-Ricci曲率;廣義復(fù)空間;半對(duì)稱度量聯(lián)絡(luò)

MR(2010)主題分類號(hào):53C40O186.12

?date:2014-09-13Accepted date:2015-11-09

Supported by the Foundation for Excellent Young Talents of Higher Education of Anhui Province(2011SQRL021ZD).

Biography:He Guoqing(1979-),female,born at Chaohu,Anhui,lecturer,major in differential geometry.