Baryogenesis in f(R,T)Gravity?
Kourosh Nozari and Fateme Rajabi
1Department of Physics,Faculty of Basic Sciences,University of Mazandaran,P.O.Box 47416-95447,Babolsar,Iran
2Research Institute for Astronomy and Astrophysics of Maragha(RIAAM),P.O.Box 55134-441,Maragha,Iran
AbstractWe study gravitational baryogenesis in the context of f(R,T)gravity where the gravitational Lagrangian is given by a generic function of the Ricci scalar R and the trace of the stress-energy tensor T.We explore how this type of modified gravity is capable to shed light on the issue of baryon asymmetry in a successful manner.We consider various forms of baryogenesis interaction and discuss the effect of these interaction terms on the baryon to entropy ratio in this setup.We show that baryon asymmetry during the radiation era of the expanding universe can be non-zero in this framework.Then,we calculate the baryon to entropy ratio for some specific f(R,T)models and by using the observational data,we give some constraints on the parameter spaces of these models.
Key words:baryogenesis,modified gravity,observational data
1 Introduction
Observational evidences,such as Big-Bang Nucleosynthesis(BBN)[1]and measurements of CMB combined with the large scale structure of the universe data[2]indicate that matter in the universe is dominant over antimatter. Recent studies suggest that the origin of asymmetry between matter and antimatter goes back to the early universe,before of the Big Bang Nucleosynthesis(BBN).[3?8]The origin of the baryon asymmetry is a fundamental question of modern physics.Theories that try to explain how the asymmetry between baryon and antibaryon was generated during the early universe belong to the realm of Baryogenesis.Many theories suggest different interactions beyond the standard model to explain the origin of this asymmetry in the primordial universe.These are GUT Baryogenesis.[9]Affleck-Dine Baryogenesis,[10?12]Thermal Baryogenesis,Electroweak Baryogenesis,[13?14]Spontaneous Baryogenesis[15?17]and Baryogenesis through evaporation of primordial black holes.[18]This mechanism was further studied in Refs.[19–29].
In 1967,Sakharov proposed three conditions that are necessary to generate a baryon asymmetry:[30](i)baryonnumber non-conserving interactions;(ii)C and CP violation;(iii)out of thermal equilibrium.Sakharov described a scenario that a universe which was initially contracting with equal and opposite baryon asymmetry to that existing today,goes through a bounce at the singularity and reverses the magnitude of its baryon asymmetry.[8]Recent studies have shown that it is possible to generate a baryon asymmetry by using some of these three conditions.Cohen and Kaplan[5]have suggested a model to generate the baryon number asymmetry by violation of CPT,while the thermal equilibrium is maintained.As shown in Ref.[20],a dynamical violation of CPT(and also CP)may give rise to the baryon asymmetry during the expansion of the universe while the thermal equilibrium is still maintained.
The issue of baryogenesis in modified theories of gravity has been studied by some authors.Baryogenesis in f(R)theories of gravity is studied in Ref.[21].Gauss-Bonnet gravitational baryogenesis is studied in Ref.[25].The authors in Ref.[26]have studied gravitational baryogenesis in f(T)gravities where T is torsion scalar. The issue of gravitational baryogenesis in Gauss-Bonnet braneworld cosmology has been studied in Ref.[27].Authors in Ref.[28]have studied gravitational baryogenesis in nonminimally coupled f(R)theories.
Gravitational baryogenesis has not been studied in f(R,T)-theories of gravity so far.Here T is the trace of the stress-energy tensor. We are going to fill this gap in this paper.It is interesting to note that energymomentum squared gravity[31]lies well in this category.With these motivations,in this paper we study gravitational baryogenesis mechanism in the framework of f(R,T)gravity,where f is a generic function of the Ricci scalar R and trace of the stress-energy tensor T.This modified gravity theory was introduced firstly in Ref.[32].The cosmological aspects of this model were studied in Refs.[33–35].The author in Ref.[36]analyzed energy conditions for this modified gravity.Thermodynamics of Friedmann-Robertson-Walker(FRW)spacetimes within this model has been studied in Refs.[37–38],and also the possibility of the occurrence of future singularities has been studied in Ref.[39].Some more aspects of this model have been studied in Refs.[40–43].Our motivation is to explore the effect of various gravitational baryogenesis terms in several models of f(R,T)gravity.That is,in the spirit of f(R,T)modified gravity we consider possible sources of gravitational baryogenesis in details.At the end we compare our results with observational data.This analysis gives some constraints on the model’s parameters.Finally we discuss which model can successfully explain the gravitational baryogenesis in this setup.We note that after detection of gravitational waves,some severe constraints on modified theories of gravity are exerted.[44?47]As has been shown in Ref.[47],f(R)theories are supported by GW observation.Our inspection shows that f(R,T)gravities are viable at least in some subspaces of the models parameter spaces.Also consistency with current gravitational experiments,especially the results from the measurements on the solar system,is studied in Ref.[48].We note also that an important issue in baryogenesis is backreaction.About the issue of backreaction in this study,we note that the scalar degree of freedom in f(R)theories(here f(R,T)theories),the Scalaron,can be considered as a quantum field that is responsible for backreaction with produced baryons and therefore baryon asymmetry.So,with this viewpoint on the involved scalarfield,the issue of backreaction in our setup can be studied in the same line as Ref.[49].
This paper is organized as follows:In Sec.2 we present a brief review of f(R,T)gravity in order to provide required notations and equations.In Sec.3 we introduce some important parameters related to baryogenesis and then we study gravitational baryogenesis in various models which are proportional to ?μR,?μT or ?μf(R,T)in the context of f(R,T)theories.We calculate the baryon to entropy ratio in each model and compare our results with observational data.We show how modified gravities can produce viable baryon asymmetry factor.The last section is devoted to a summary and conclusions.
2f(R,T)Gravity
Many alternative models of classical or quantum gravity have been proposed to explain the late time accelerated phase of the universe expansion.f(R,T)modified theories of gravity are one of the interesting models to explain the current expansion of the universe.This theory is based on the coupling between geometry and matter.The study of this theory leads to some interesting features,which could distinguish and discriminate between various gravitational models.f(R,T)models can describe the transition from the matter dominated phase to the late times positively accelerated phase.[33]The gravitational Lagrangian for these theories is a generic function of the Ricci scalar curvature R and the trace of stress-energy T.The action with inclusion of matter reads
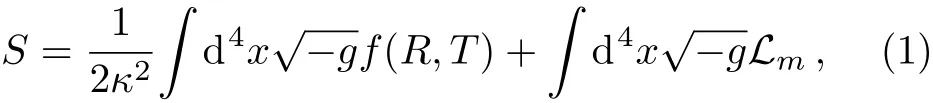
where Lmis the matter Lagrangian density.We define the stress-energy tensor of the matter fields as
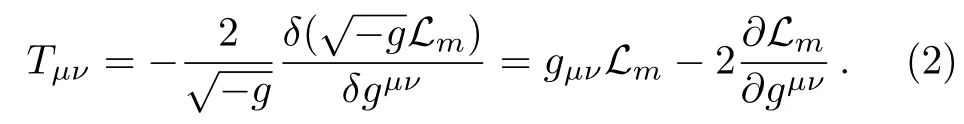
The field equations are obtained by varying action(1)with respect to the metric which is as follows
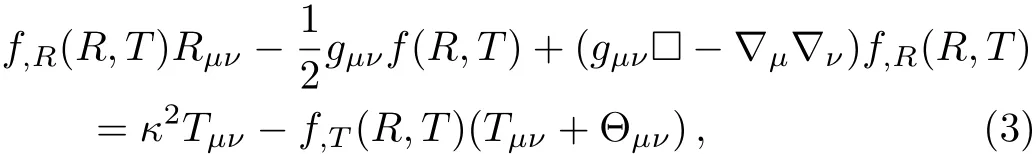
where f,X≡ df/dX.In this relation Θμνis defined as

The trace of the field equations(3)becomes
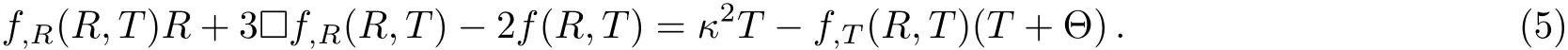
By using this relation we rewrite the field equations(3)as follows
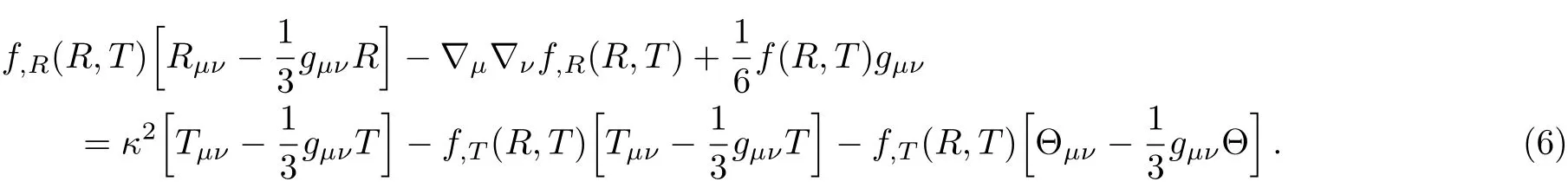
Taking covariant derivative of the field equations(3)leads to
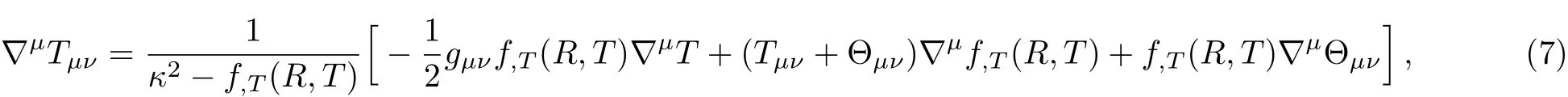
where we have used the identities?μ(Rμν?(1/2)gμνR)=0,and(?μ????μ)f,R=Rμν?νf,R.Equation(7)shows that the usual conservation law does not satisfy in f(R,T)models.So,a test particle that is moving in a gravitational field as described here,does not follow a geodesic in the sense of General Relativity.In fact,the coupling between matter and geometry in this framework induces an extra acceleration acting on the particle.This is because of the interaction between the matter and curvature sectors.This non-conservation of the standard matter leads essentially to violation of the usual global evolution(as supported by observation)of the different species in the universe.Then for Θμν,by using Eqs.(2)and(4),we derive
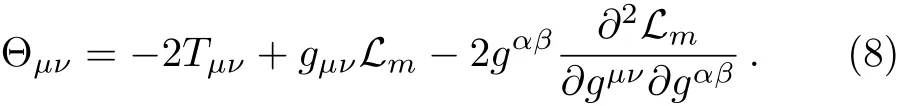
We consider the universe to be filled with a perfect matterfluid with the stress-energy tensor
where uμis the four-velocity with uμuμ= ?1.ρmand pmare the energy density and pressure of the matter fields that we assume to be related as pm= ωmρm,where ωmis the equation of state parameter.In this case,by comparing Eqs.(2)and(9)the matter Lagrangian can be set as Lm=pm.Therefore,the tensor Θμνyields
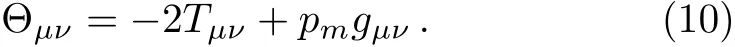
Now,the field equations(3)can be written as
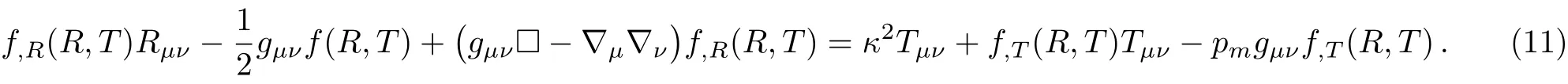
Now,we consider the metric of the universe to be a flat Friedmann-Robertson-Walker metric
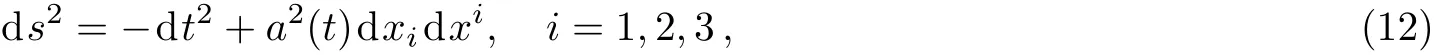
where a(t)is the scale factor.Thus,we obtain the tt and ii components of the field equations(11)as follows
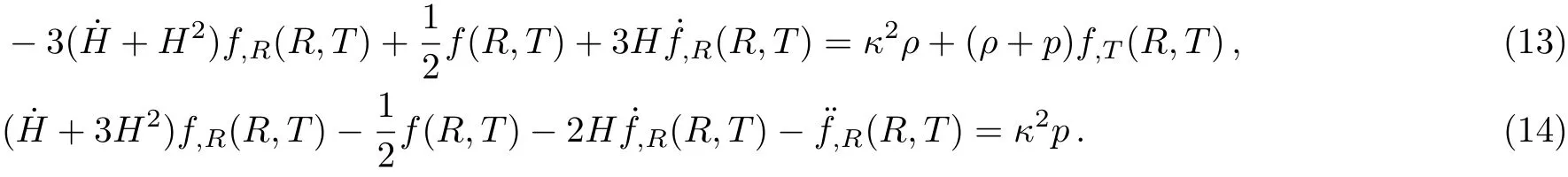
Also Eq.(5)gives

In the specific class of f(R,T)as f(R,T)=f1(R)+f2(T)where f1(R)and f2(T)are arbitrary functions of R and T,Eq.(7)reads as
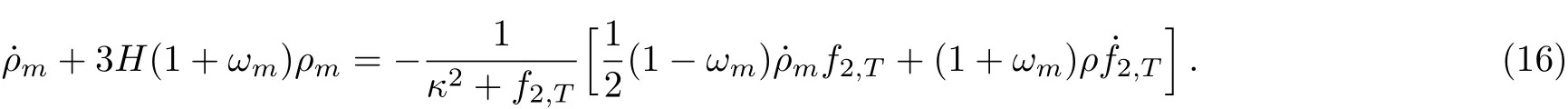
This equation shows that the stress-energy tensor of the matter fields is not conserved.The covariant conservation of stress-energy tensor,Tμν,of the standard matter is an essential feature in standard general relativity,which is a direct consequence of the diffeomorphism invariance of the theory.So,it is expected that any classical gravitational theory should satisfy such a requirement as well to give usual global cosmic evolution of the standard species.For this purpose the right hand side of Eq.(16)must be zero,which gives the following constraint

where ωm=1/3.The general solution of this differential equation is
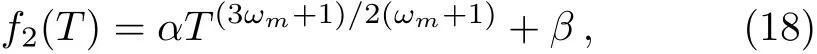
where α and β are integration constants. For the barotropic equation of state ωm=0,the dust,we obtain
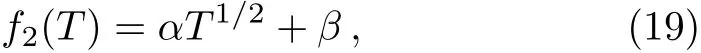
This function represents the only case in which the usual continuity equation is satisfied for a dust fluid.
3 Baryogenesis inf(R,T)Gravity
In this section we show how f(R,T)theories can explain asymmetry between matter and antimatter.One of the important quantities used to calculate such asymmetry is the baryon asymmetry factor ηBas
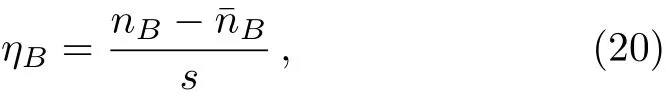
where nB(ˉnB)is the baryon(antibaryon)number density,and s is the entropy of the universe.Some observational data such as Cosmic Microwave Background(CMB)anisotropies and Big Bang Nucleosynthesis(BBN)have confirmed that the order of magnitude of this asymmetry is ηB≤ 9 × 10?11.[3,28,50]Now,we propose a mechanism that generates a baryon asymmetry that is observationally acceptable,while the thermal equilibrium is maintained.The interaction between the derivatives of the Ricci scalar R and the baryon-number current J breaks CPT dynamically in an accelerated universe.The CP-violating interaction term is given as
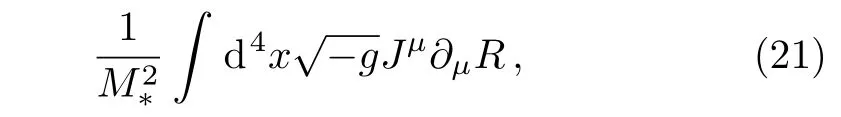
where M?is the cuto ffscale of underlying effective theory and Jμis the baryonic matter current.g and R are the trace of the metric tensor and the Ricci scalar respectively.This relation can be acquired in Supergravity theories from a higher dimensional operator.[51]We note that a similar mechanism of spontaneous baryogenesis has been studied in Ref.[52],where a CP-violating interaction term comes from a Supergravity interaction.This is another scenario of spontaneous baryogenesis in the lowenergy effective theory of Supergravity.
If we consider a flat Friedmann Roberson Walker(FRW)metric,the effective chemical potential for baryons according to equation(21)isμB=(for antibaryons=?μB).The net baryon number density at the equi-librium in the regime T ? mBis given by nB=gbμBT2/6 where gbis the number of intrinsic degrees of freedom of baryons.So,the baryon to entropy ratio in the expansion of universe,after the temperature of the universe drops below the critical temperature TD,becomes[20]
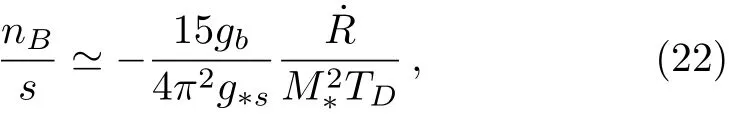
where s=2π2g?sT3/45.TDis the temperature in which the baryon asymmetry generating interactions occur and g?srepresents the total degrees of freedom for particles that contribute to the entropy of the universe.In order to have nB/s=0,the time derivative of the Ricci scalar must be non-zero.At this point we should stress on an important issue regarding Eq.(22):We have assumed that the baryon asymmetry generating interactions occur at T=TDand then we use Eq.(22)for this purpose.However,as has been stated thoroughly in Ref.[52],it is not clear if Eq.(22)can be justified in a generic situation.For instance,in the context of spontaneous baryogenesis,it is usually assumed that the B-L asymmetry is generated by the scattering of heavy right-handed neutrinos.In this case,the backreaction(which we have commented previously)of B-L breaking effect is important and the result cannot be simply written as Eq.(22).Here we neglect these complications as this is a first study of baryogenesis in f(R,T)theories.We are going to fill these gaps in another study.
In the context of standard Einstein-Hilbert gravity,[20]the Ricci scalar is related with trace of the stress-energy tensor as
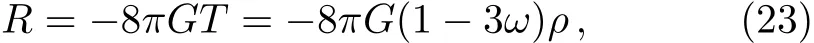
where ρ is the energy density with the equation of state parameter,ω =p/ρ and p is the pressure of matter.This equation shows that in the radiation dominated era with equation of state parameter ω=1/3 the Ricci scalar and its time derivative are zero.So,in this way no net baryon number asymmetry can be generated in radiation dominated era.
Now we study the baryogenesis mechanism in some specific models of f(R,T)theories and show how these models are capable in essence to generate baryon asymmetry.We show that in this setup the baryon to entropy ratio is not zero,even in the radiation dominated epoch.
?A simple f(R,T)model
As a first case of f(R,T)modified gravity models we choose a simple form of f(R,T)as
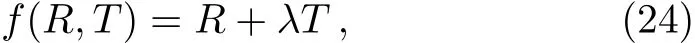
where λ is a constant.We note that constraint on λ to have a cosmologically viable scenario with this choice can be found in Ref.[42].For this type of f(R,T)the gravitational field equations are given by
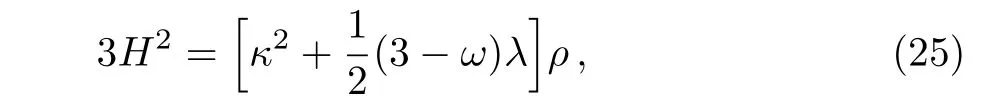
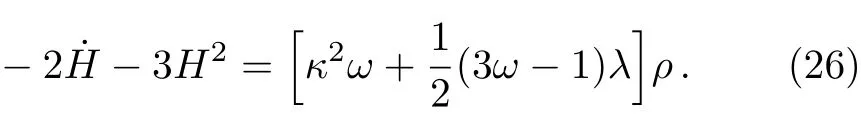
By contracting these equations we get
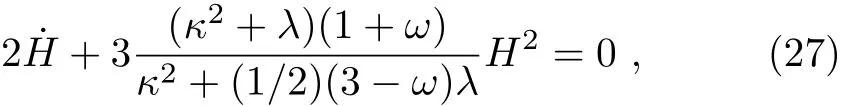
and by solving this differential equation we obtain

where
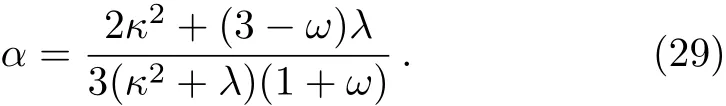
This solution implies the scale factor of the form a(t)~ tα.Using Eq.(24)and by substituting Eq.(28)into Eq.(16),we obtain

We can find the parameter ρ0by using Eq.(25)as
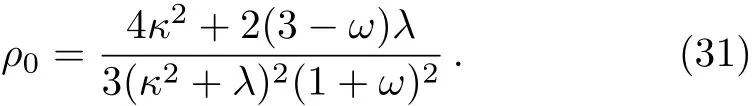
For the flat FRW metric,the Ricci scalar is given by

So,by using Eq.(28)we obtain the time derivative of the Ricci scalar as follows
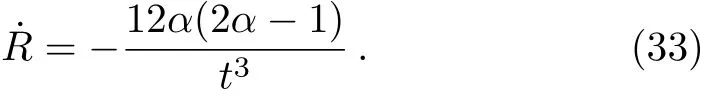
The energy density is related to the temperature T as[3]

By using this equation and energy density(30)we canfind the decoupling time as a function of decoupling temperature TDas

Inserting this equation into Eq.(33)and using Eq.(22)we obtain the baryon asymmetry factor as
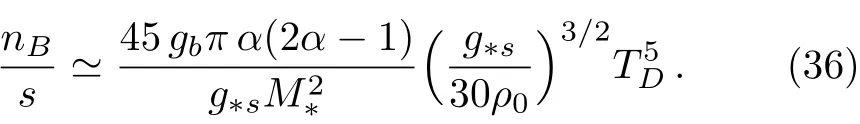
This equation shows that the resulting baryon to entropy ratio is non-zero even for radiation dominated era(the radiation domination case corresponds to ω=1/3).Following Ref.[20],our choice of the cuto ffscale M?iswhere mplis the Planck mass,the decoupling temperature is TD=MIwhere MI~2×1016GeV is the upper bound on the tensor mode fluctuation constraints on the inflationary scale.This choice is particularly interesting because it implies that tensor mode fluctuations should be observable in experiments;the expectation that finally has been approved by detection of gravitational waves in last year.Also we assume gb~O(1)and g?s=106.The resulting baryon to entropy ratio could be very large in comparison with the observed value.So,it seems that this model gives physically unacceptable result for baryon asymmetry.This is because we have assumed that TDis as high as the upper bound on the tensor mode fluctuation constraints.However,if one adopts a lower TD,the situation changes drastically and the resulting baryon asymmetry could be acceptable in comparison with observation.For instance,we see from Eq.(36)that the baryon asymmetry can be smaller by a factor of 10?10if we decrease TDby a factor of 10?2.So,this simple model can be viable observationally in some subspaces of the model parameter space.
To derive physically consistent predictions in a wider region of the parameter space we are forced to consider more complicated models of f(R,T)gravity.
?The Case with f(R,T)=f(R)+λT
Now we consider the function f(R,T)as given by f(R,T)=f(R)+λT.In this case the field equation(13)reads
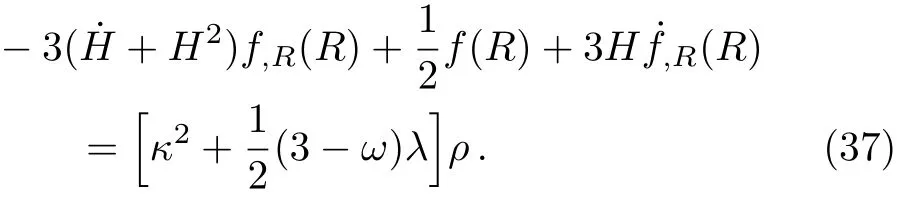
We assume the cosmic evolution of the universe to be described by a(t)~tn.To derive an exact solution,we consider f(R)=R+ξRmwhere ξ is a constant.So,from Eq.(37)we obtain the energy density at leading order as

where
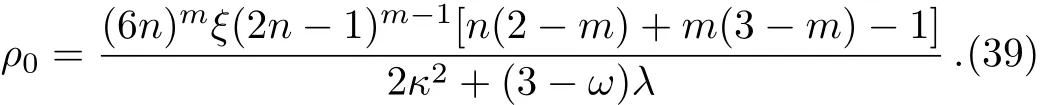
Equations 16)and(38)now imply
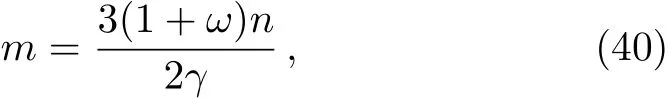
where
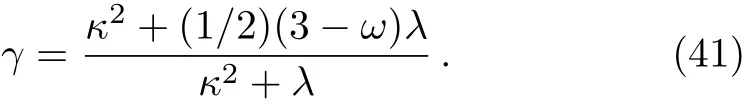
Then,by using Eqs.(34)and(38)the decoupling time can be obtained as
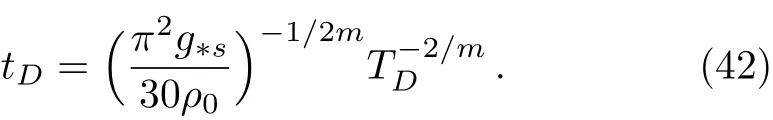
Therefore,the baryon to entropy ratio becomes

which is non-zero for the radiation dominated era.In order to compare our results with observational data we must choose viable values for the free parameters of the theory.We choose the cuto ffscale M?and TDas before.Also we assume gb~ O(1),g?s=106 and n=0.6.To satisfy the observational constraint nB/s.9.2×10?11,the parameter m must be restricted to the values with m>1.8(note that the case with m=2 is the famous Starobinsky model).For example,for m=1.8 and ξ=102,the baryon to entropy ratio gets nB/s? 3.9×10?11,which is in good agreement with observations.We note that there is a wide range of values for the parameters m and n,which can provide acceptable result in comparison with observations.
?The Case with f(R,T)=A(1? e?qR)+λT
Let us consider exponential f(R)gravity where A and q are the model parameters.In this case,the field equation(13)at leading order gives
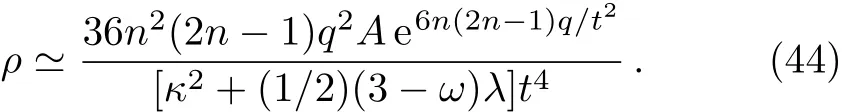
The decoupling time tDis related to the decoupling temperature TDas follows
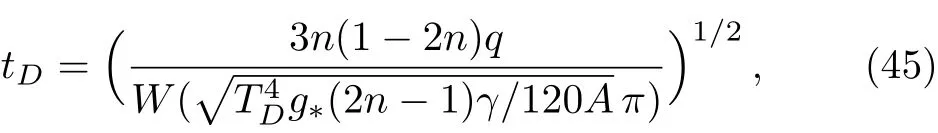
where γ = κ2+(1/2)(3 ? ω)λ and W(z)is the Lambert function.Hence,the resulting baryon to entropy ratio would be as follows
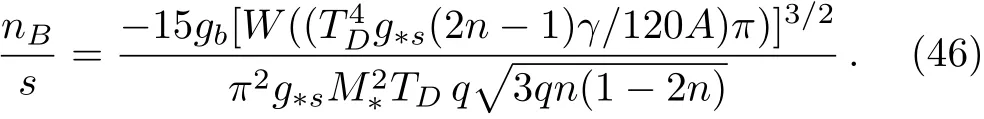
Then,for MI~2×1016GeV,TD~ 2×1016GeV,n=0.6,λ =A=1 and q= ?10?8the baryon to entropy ratio gives nB/s? 6.7×10?11which is in good agreement with observations.
4 Coupling of the Baryon Current with Stress-Energy Tensor
In this section we introduce another form of the baryogenesis interaction in which the derivatives of the trace of the stress-energy tensor T are coupled with the baryon current Jμ.Then we obtain the baryon to entropy ratio in this case.We consider the CP-violating interaction term as
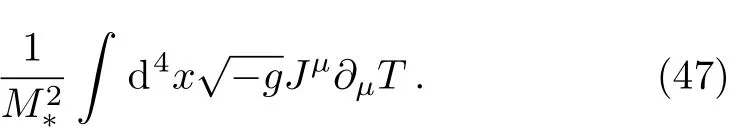
In this case,the baryon to entropy ratio becomes
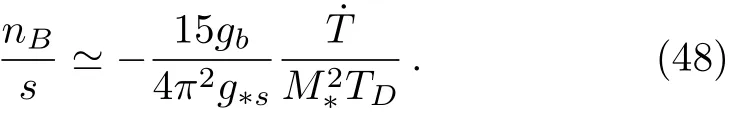
Now,we investigate this scenario in some specific models of f(R,T)gravity.Depending on different models,the baryon to entropy ratio gets different numerical values.
?The Case with f(R,T)=R+λT
In this case Eq.(15)becomes
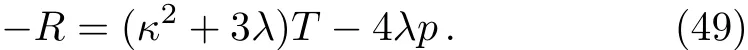
Using a(t)and ρ(t)as we have derived previously,Eq.(49)gives

where
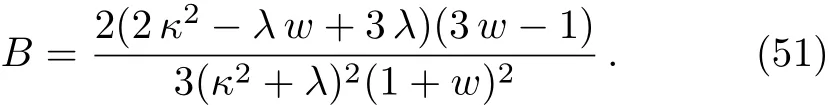
Then,by using Eq.(35)the resulting baryon to entropy ratio becomes
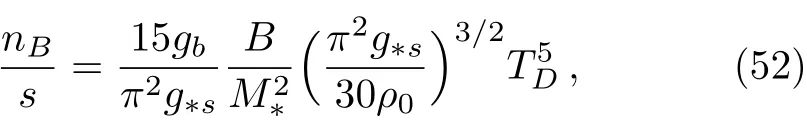
which shows that the baryon to entropy ratio is zero for radiation dominated era(since B=0 for w=1/3).This means that baryon asymmetry can not be generated in this specific model.
?The Case with f(R,T)=R+ξRm+λT
In this case,by using Eq.(15)and field equations at leading order we obtain

where
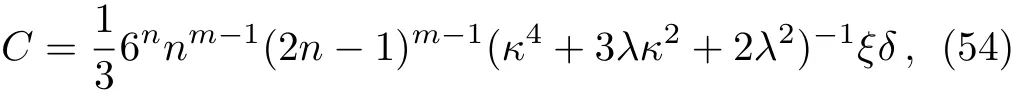
and
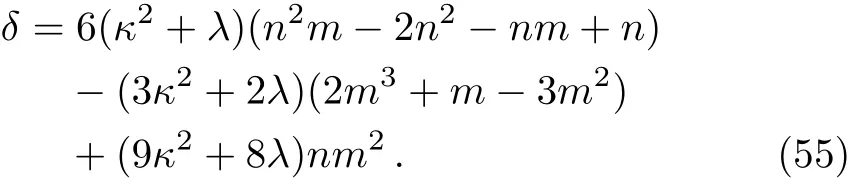
Using Eqs.(39)and(42)the baryogenesis factor gets the following form
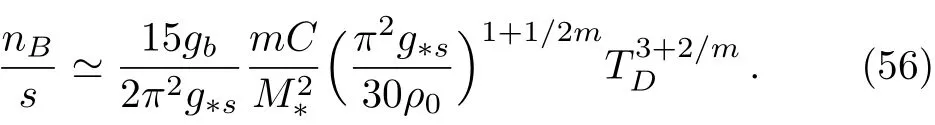
So,by choosing TDand M?as before and also by setting n=0.6,ξ=?106,m=?0.5,the baryon to entropy ratio is find as nB/s? 2.6×10?11which is very close to the observed value.
?The case with f(R,T)=A(1? e?qR)+λT
Following the same procedure,in this model the baryon to entropy ratio at leading order is given approximately as
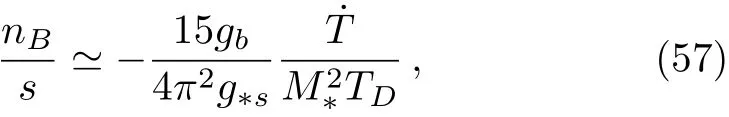
where
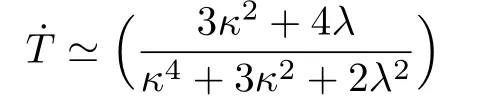

The relation between tDand TDcan be derived as in Eq.(45).While this relation is so lengthy and therefore we avoid to present it here,it is negative and therefore unacceptable.This shows that there is an excess of antimatter over matter which is not physical on observational ground.This means that the modified gravity of this type is not viable from baryogenesis viewpoint in essence.
5 A More Generalized Baryogenesis Interaction Term
Let us now to consider a more general baryogenesis interaction term as
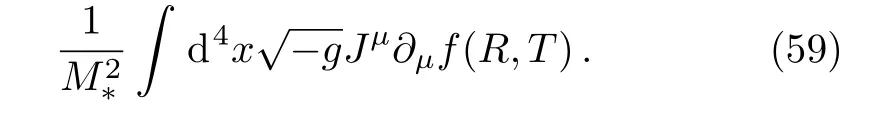
Thus,the baryon to entropy ratio is calculated as
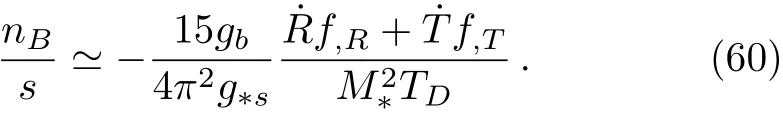
To proceed further,we consider a power law scale factor a(t)~tnand then apply Eq.(60)to three models of f(R,T)gravity as introduced in previous parts.
?For the model of Eq.(24),the baryon to entropy ratio is obtained as
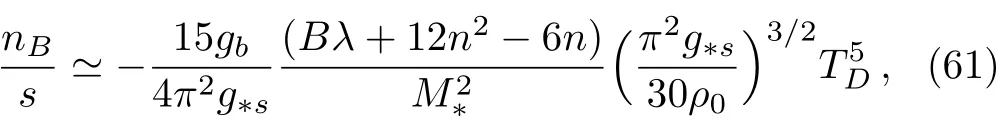
where B is given by Eq.(51).This ratio,is either negative in some subspaces of the model parameter space or extremely large in comparison to the observed value.So,this type of modified gravity is not viable from brayogenesis point of view.
? For the model with f(R,T)=R+ ξRm+ λT we obtain

where C is given by Eq.(54).We insert this relation into Eq.(60)and then by using Eq.(42)we find

If we choose M?and TDas before and set m= ?2 and ξ= ?11,the resulting baryon to entropy ratio at leading order gives nB/s? 4.7×10?11which is in very good agreement with observations.So,from baryogenesis viewpoint,this modified gravity is reliable,at least for some subspaces of the model parameter space,observationally.
?Finally,for the case with f(R,T)=A(1? e?qR)+λT we obtain
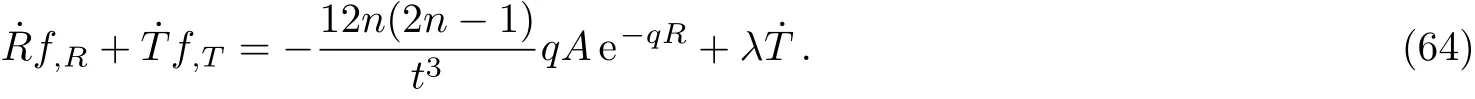
By inserting this result into Eq.(60)and using the decoupling time(45),we obtain the baryon to entropy ratio in leading order as
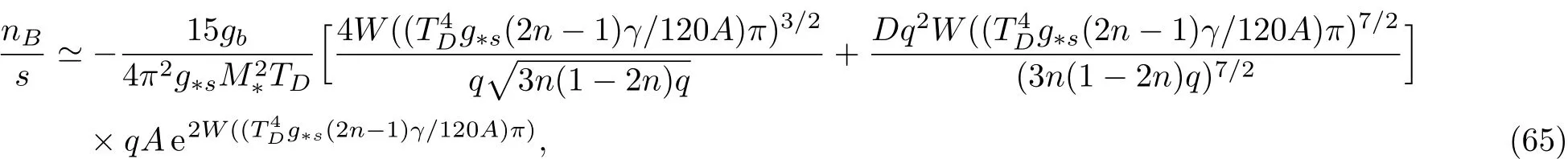
where by definition,
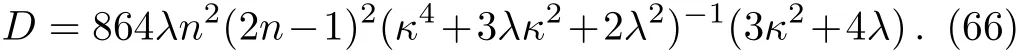
The ratio nB/s is negative in this case,which is unacceptable on observational ground.
6 Summary and Conclusion
One of the unsolved problems in cosmology is the excess of matter over antimatter in the universe.Gravitational baryogenesis is one of the mechanisms that have been proposed for the generation of baryon-antibaryon asymmetry.In this work we have studied the gravitational baryogenesis scenario in the framework of modifi ed f(R,T)gravity.We have shown that how modified gravity of the type f(R,T)is capable to explain the observed asymmetry between matter and antimatter.We have considered three cases of f(R,T)gravity and investigated various forms of baryogenesis interaction in these cases.In the first and simplest model,corresponding to f(R,T)=R+λT,the obtained baryon to entropy ratio is not acceptable on observational ground if we assume TDto be as high as the upper bound on the tensor modefluctuation constraints.In fact,observational data from CMB anisotropies and BBN give ηB≈ 9 × 10?11for the magnitude of baryon-antibaryon asymmetry.But there are other reliable choices in essence.Actually,there is the possibility of observational viability of this simple model in some subspaces of the model parameter space.For instance,if we decrease TDby a factor of 10?2,the resulting baryon asymmetry parameter can be smaller by a factor of 10?10,well in the range of observation.To proceed further and in order to get physically acceptable results in a wider region of parameter space we considered more complicated models.The case of f(R,T)=R+ ξRm+ λT is an interesting model in our analysis.We showed that in this case the baryon to entropy ratio is consistent with observationally confirmed value,at least in some subspaces of the model parameter space.As we have emphasized in our analysis,the parameters of models have important role in calculation of the baryogenesis factor.An important result of this type of modified gravity is that in contrast to the standard gravitational baryogenesis mechanism,in this case the baryon to entropy ratio is non-zero even for a radiation dominated universe.Another point to note is that the observationally confirmed value of baryon-antibaryon asymmetry gives some important constraint on the model’s parameters.Another case,f(R,T)=A(1? e?qR)+λT,has been treated also and gives observationally viable result for the mentioned asymmetry in some subspaces of the model parameter space.For instance,with MI~2×1016GeV,TD~ 2×1016GeV,n=0.6,λ =A=1,and q= ?10?8,the baryon to entropy ratio in this model is given by nB/s?6.7×10?11which is in good agreement with observationally supported value.We have extended our study to the case that the baryon current is coupled to the derivatives of the trace of the stress-energy tensor and then we have studied some specific models in this framework.Finally we have studied a more general baryogenesis interaction term so that the baryon current is coupled to ?μf(R,T).We studied the effect of this general interaction term on the baryon to entropy ratio.In this more general case,we have shown that with the choice f(R,T)=R+ξRm+λT,the baryon to entropy ratio for some specific and viable values of the model’s parameters is obtained as nB/s ? 4.7 × 10?11,which is close to the observationally confirmed value.
As a final note,the issue of cosmological viability of the adopted f(R,T)theories is important to be discussed.Here we considered several particular cases of f(R,T)gravity,which can describe the sequence of cosmological epochs including matter dominated era and late time accelerated expansion that are important after baryogenesis.The new matter and time dependent terms in the gravitational field equations play the role of an effective cosmological constant.In the first example we considered the simplest version of f(R,T)gravity,which is the most common one in the literature.As has been shown in Ref.[34],this model is able to explain matter dominated era,but as has been shown in Ref.[42],this model does not provide the transition from deceleration to accelerated phase.There exists a subclass of this theory which is not cosmologically viable.For avoiding the appearance of singularities,the function f1(R)in these models must be non-linear in R.In the second and third examples,the matter dominated and accelerated phases have been resulted.[33]In f(R,T)scenario,an interesting point is that,contrary to f(R)gravity where ordinary matter is usually neglected,f(R,T)gravity reproduces this unification without any restriction.[33]We refer to Ref.[42]for a recent work on cosmological viability of f(R,T)gravities.In summary,here the adopted models of f(R,T)are capable essentially(at least in some subspaces of their model parameter space)to follow cosmological history,at least the sequence of matter domination and late time accelerated expansion as important epochs after baryogenesis.
 Communications in Theoretical Physics2018年10期
Communications in Theoretical Physics2018年10期
- Communications in Theoretical Physics的其它文章
- P-V Criticality of Born-Infeld AdS Black Holes Surrounded by Quintessence?
- Prospect for Cosmological Parameter Estimation Using Future Hubble Parameter Measurements?
- Topological Dark Matter from the Theory of Composite Electroweak Symmetry Breaking?
- Pair Production in Chromoelectric Field with Back Reaction?
- Impact of Internal Heat Source on Mixed Convective Transverse Transport of Viscoplastic Material under Viscosity Variation
- High Accuracy Split-Step Finite Difference Method for Schr¨odinger-KdV Equations?
