Application of Numerical Simulation for Analysis of Sinking Characteristics of Purse Seine

ZHOU Cheng, XU Liuxiong, 2), 3), 4), *, ZHANG Xinfeng, 2), 3), 4), and YE Xuchang, 2), 3), 4)

?

Application of Numerical Simulation for Analysis of Sinking Characteristics of Purse Seine

ZHOU Cheng1), XU Liuxiong1), 2), 3), 4), *, ZHANG Xinfeng1), 2), 3), 4), and YE Xuchang1), 2), 3), 4)

1),,201306,.2),,201306,.3),201306,.4),201306,.

This study applies the mass-spring system to model the dynamic behavior of a submerged net panel similar to the shooting process in actual purse seine fishing operation. Modeling indicates that there is insufficient stretching with the net panel under the floatline in the prophase of the shooting process. Sinkers at different locations along the leadline descend successively after submergence, and the sinking speed decreases gradually with elapsed time until attainment of a stable state. Designs with different current speeds and sinker weights are executed to determine the dimensional shape and sinking characteristics of the net. The net rigged with greater sinker weight gains significantly greater sinking depth without water flow. Compared with the vertical spread of the net wall in static water, the middle part of the netting presents a larger displacement along the direction of current under flow condition. It follows that considerable deformation of the netting occurs with higher current speed as the sinkers affected by hydrodynamic force drift in the direction of current. The numerical model is verified by a comparison between simulated results and sea measurements. The calculated values generally coincide with the observed ones, with the former being slightly higher than the latter. This study provides an implicit algorithm which saves computational loads for enormous systems such as purse seines, and ensures the accuracy and stability of numerical solutions in a repetitious iteration process.

numerical simulation; mass-point model; purse seine; sinking characteristics

1 Introduction

The operation of a purse seine mainly involves the netting rapidly dropping in water, quietly encircling fast-moving fish schools, and finally forming a big bowl shape by closing the bottom through hauling the purse line. Timely closing of the netting likely determines the success of fishing. The parameters of a purse seine, including netting material, weight of netting in water, hanging ratio, weight of sinkers and their distribution along the leadline, affect the behavior and performance of fishing gear. In addition, oceanographic and environ- mental factors (, current, waves, and wind speeds) as well as patterns of casting and hauling invariably influence the shape of the net. According to the literature (Kim., 2007), studies regarding the design and modification of purse seines mainly rely upon sea trials, modeling experiments, and theoretical calculations, but are riddled with difficulties, unknowns, and uncertainties.Numerical simulation is a method combining physics and mathematics, which can be used for predicting or understanding the performance and spatial movements of fishing gear during the design stage.

Fishing gear and the process of fishing underwater have been studied in the past using static mechanics resolved in analytic geometry (Machii and Nose, 1992; Liu., 1984; Niedzwiedz and Hopp, 1998; Yoshihara, 1951). Certain studies are focused on net components (.., flexible ropes) or net panels by looking at the physical and geometrical aspects (Li., 2006). The form of motion can be described using a series of statics formulas and displayed in an equilibrium state (Wan., 2002). Due to the interaction between force and motion of the flexible structure, it’s nearly impossible to derive a formula applicable for the entire system of a purse seine (Hosseini., 2011). Even if there are numerous expressions used for the complicated structure, the difficulty remains in obtaining analytical solutions because they involve solving many nonlinear equations.

The sinking performance of purse seine was previously investigated via model experiments in natural water and full-scale measurements at sea. Xu(2011a) studied a model net, which was reduced by twenty times in the main dimension based on similarity criteria obtained with the lake, and concluded that the purse seine sinks faster when increasing the weight of the leadline. Xu(2011b) then analyzed data collected from fishing operation at sea and found that the highest sinking speed of purse seine occurs at the rear wing end, followed by the middle part and the bulk. Kim (2004) described the same sinking characteristic of purse seine after analyzing models made with different netting materials. Compared with theoretical analysis, these experiments are generally practical but expensive and time consuming. Additionally, the modeling results are inadequate due to restricted experimental conditions. Moreover, further research is needed to determine whether model gear constructed according to the modeling law can totally reflect the prototype net in terms of performance.

Over the last two decades, numerical simulations have been proposed as an effective approach for dealing with difficulties unresolved by other methods. In particular, recent advances in the finite element theory as well as the computer technology have made dynamic simulation of fishing gear possible. According to the finite element theory, flexible structures can be divided into many simple and interconnected units, and approximate solutions can be obtained with the assumptions of initial values and numerical calculations. Presently, numerical simulation is being widely used in studies of fish cages (Huang., 2006; Zhao., 2010, 2007), longline (Lee., 2005b; Wan., 2005; Song., 2011) and trawl nets (Hu., 1995; Lee and Cha, 2002; Lee, 2005a). There has been an increasing tendency for numerical simulations in studies of the physical performance of fishing gear over the last decade.

For purse seines, Lee. (2005a) described a flexible system composed of a network of masses and springs, using an implicit integration method to simulate the shape of a net during the shooting and pursing processes in calm water. Kim. (2007) applied a mass-spring model and developed a simulation tool to automatically generate a mathematical model from a gear-design drawing. The accuracy of the mathematical model was verified by comparing the data from field measurements with model calculations. Considering fishing vessel movement and detailed sea conditions, Kim and Park (2009) established a three-dimensional geometric model using finite element methods. Additionally, Hosseini. (2011) refined a mass-spring model by taking into account the drag coefficient as a function of attack angle and Reynolds number, and examined the sinking performance of different net designs through numerical simulation.

The present study employs the lumped mass method to dynamically simulate the casting process of a purse seine, providing an implicit algorithm which saves the computational loads for enormous system such as purse seine and simultaneously ensures the accuracy and stability of numerical solutions in a repetitious iteration process. For model verification, the simulated results are compared with measurements of depth recorder during fishing operation at sea. Further, the effects of current speed and sinker weight on the behavior of the netting underwater are quantified to examine the sinking characteristics of the purse seine.

2 Numerical Simulations

2.1 Structural Modeling

The structure of a purse seine mainly consists of netting, floats, sinkers and ropes. Netting and ropes are considered as flexible objects, while floats and sinkers are regarded as sphere-like geometric units. In this study, a mass-spring system is adopted to model the physical system,., the flexible structure is divided into finite elements interconnected by springs.

To simplify the model, we consider the mesh bars as springs without mass and the knots as mass points. All external forces such as gravity, buoyancy, and drag acting on the twines are averagely concentrated on the mass points along the edge of bars. Similarly, the tensile force resulting from the elasticity of the spring works on the mass point. In regard to other components, ropes are divided into many mass points connected by springs with the same characteristics mentioned above. The sinkers and floats appended to the structure are also considered as mass points.

The shape of the netting in water changes continually with varied forces acting on it. The intensity of these forces depends on the configuration of the structure. The netting is also subject to deformation due to the movement of coordinates for the mass points. Consequently, the establishment of a network matrix aims to effectively record the displacement of the mass points at different times. The ordered arrangements of knots facilitate distinguishing and marking the position of each mass point.

2.2 Equation of Motion

The geometric shape of a purse seine depends on the resultant force vectors, including the sinking force, buoyancy, tensile force,and hydrodynamic force(Fig.1). The basic kinematic formula of the mass point with accelerationcan be expressed as:

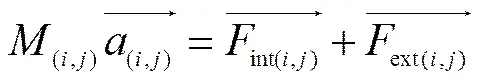
where(i,j)is the mass of the mass point (,);is the acceleration of the mass point in motion;intis the internal forces acting on the mass point,., the tensile forces of the spring between closely adjacent mass points; andextis the external forces acting on the mass point, including drag, lift, gravity, and buoyancy.

The internal force, acting on the spring between two directly adjacent mass points is a function of linear elongation of the spring. The internal forces on each mass point can be represented by the following equation:

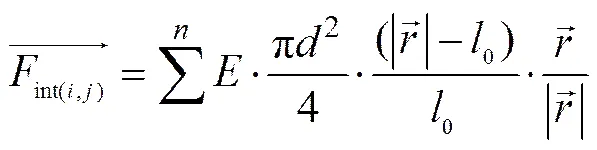
wherethe is elastic modulus of the bar,is the diameter of the bar,0is the initial length between mass points,is the position vector from the mass point to its adjacent mass point andis the number of other mass points around the mass point.

Buoyancy and gravity of a mass point can be represented as follows:

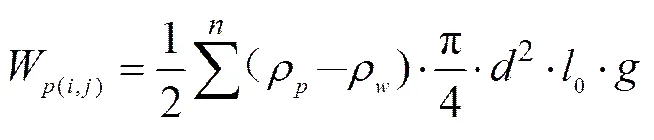
whereWis the resultant force of buoyancy and gravity in the vertical direction,ρis the density of twine, andρis the density of sea water.

The hydrodynamic forces consist of the drag forceFand the lift forceF, given by the following formulas:

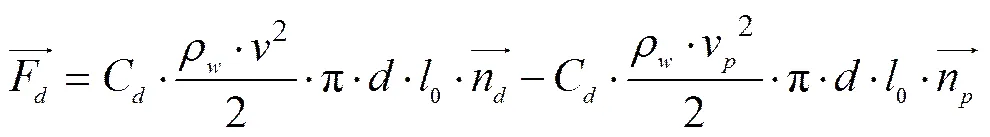
whereCis the drag coefficient,is the magnitude of water flow velocity,is the unit vector of water flow,vis the magnitude of particle velocity, andis the direction vector of particle motion.

, (5)

whereCis the lift force coefficient,is the magnitude of current velocity, andis the unit vector of the lift force which is perpendicular to the direction of the drag force and is expressed as follows:

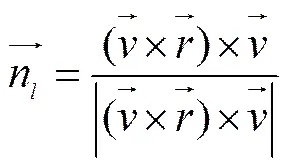
The drag and lift force coefficients are important parameters that affect the shape of fishing gear. Many studies on this topic have been conducted but have not yet widely accepted (Lee., 1998; Paschen and Winkel, 2002; Aarsnes., 1990). In this paper, we adopt the theory proposed by Hoerner (1965) and employ the following formulas to estimate the drag and lift force coefficients:

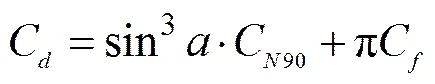
whereis the attack angle, Cis the friction coefficient (πC=0.02, according to Hoerner’s cylinder theory), andC90is the hydrodynamic coefficient at an attack angle of 90? (C90=1.1), withdefined as follows:

,. (8)

In a reference frame, according to the second law of Newton, the basic dynamic formula of the mass point (,) can be expressed as:

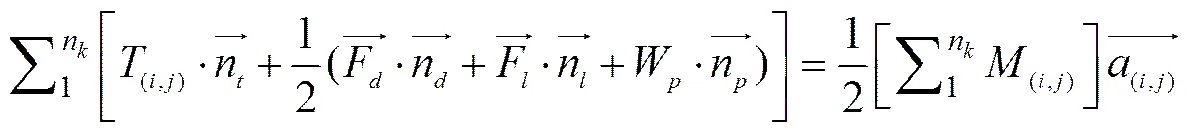
wherenis the number of adjoining mass points around the mass point (,).

In physics, acceleration is the second-order derivative of the displacement, while velocity is the first-order derivative. Therefore the differential equations of motion decomposed along the coordinate axes of,, andcan be written as:

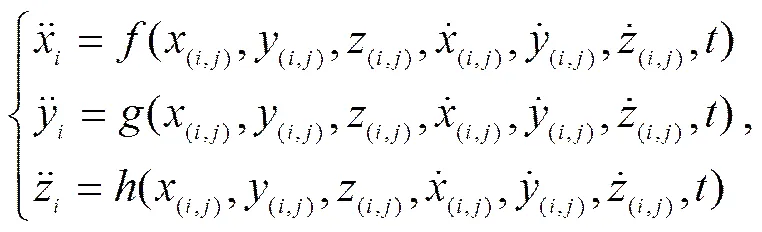
where(i, j),(i, j),and(i, j)are the displacements for the mass point (,).

Eq. (10) is a second-order nonlinear differential equation group, and a descending process is thus required to decrease the order. Here we define:

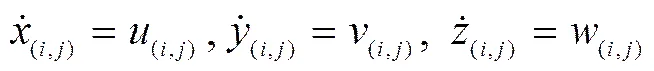
where(i, j),(i, j), and(i, j)denote the velocity components of the mass point (,) along the axes of,, and, respectively.

As a consequence, the equations are converted to first- order differential equations as:

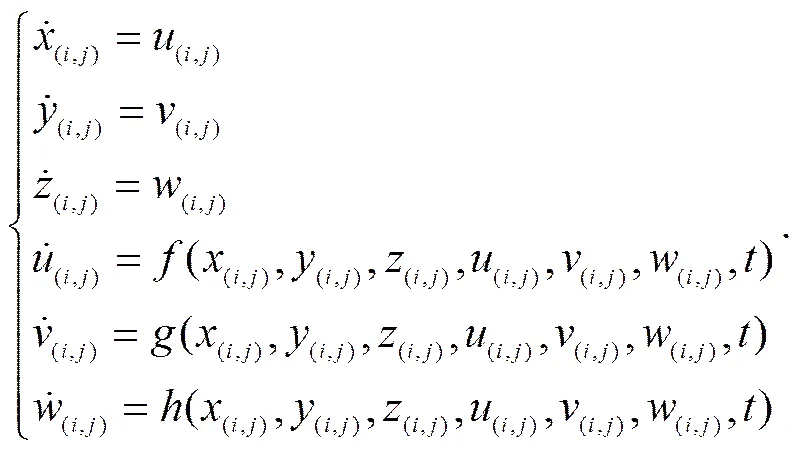
2.3 Numerical Calculation

The solution of the first-order differential equation is converted numerically to calculate the-th step of the implicit iteration with given initial values under certain conditions. As it is a stiff equation sensitive to the algorithm, an implicit predictor-corrector method is used at the-th iteration to ensure the precision and stability of the numeric solution. The-th iteration is acquired using the Euler method:

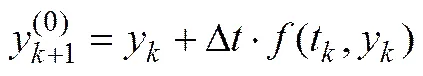
The corrector procedure is repetitiously modified with a trapezoid formula:

,

2.4 A Case for Simulation

Despite that more mass points are more effective for showing a realistic shape, the computational time would be greatly increased with addition of meshes and mass points. To simplify the structure and lessen the calculation load, a rectangular net panel was approximated to the purse seine model. The net was made of knotless nylon netting with forty meshes in the transverse direction and eight meshes in the longitudinal direction. The length and diameter of the mesh bars were 100 and 1.4mm, respectively. A total of 40 iron spheres were attached at the bottom of the netting to supply the sinking force. The sinkers were divided into two levels, called GW1 (diameter 10mm) and GW2 (diameter 6mm). The shape and sinking depth of the model net were examined at tidal current speeds of 0, 0.05, and 0.2ms?1.

In the simulation of the purse seine operation, it is assumed that a normal circle is formed by the floatline with a casting speed of 0.63ms?1. As net panel gathers on the deck in an actual casting situation, all mass points are fastened together to locate uniform coordinate. Once the simu- lation gets started, the purse seiner tows the front end of the net at a certain speed, with the other end dropping into water without initial speed in the vertical direction. Mass points submerge in sequence following the motion of the vessel and sinking of the net under the action of gravity.

3 Simulation Results

In the simulation of the pursing process, environmental conditions, including the bottom type which may affect operation of the gear in shallow water, need to be considered for appropriate results. Consequently, the pursing and current speed must be input before each simulation begins. Fig.2 shows the pursing process at a casting speed of 0.63ms?1without tidal current (2-s time interval for the continuous stage). In the initial stage of pursing, mass points gained on the lower edge of the netting speeded up the sinking rate, while net panels under the floatline did not fully spread out.

Fig.2 The continuous process of netting shape change at the shooting speed of 0.63ms?1 without water flow.

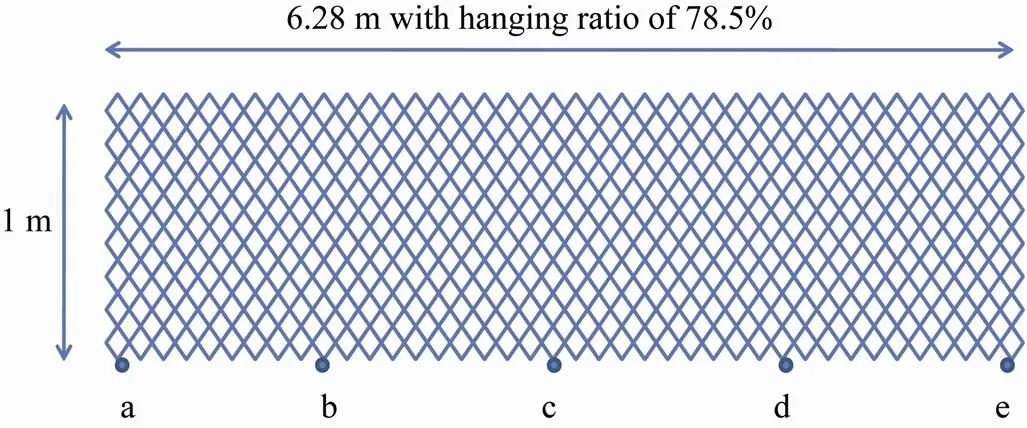
Fig.3 Configuration and dimension of an undeformed sample net and designation for the position of examined points a through e on the leadline.

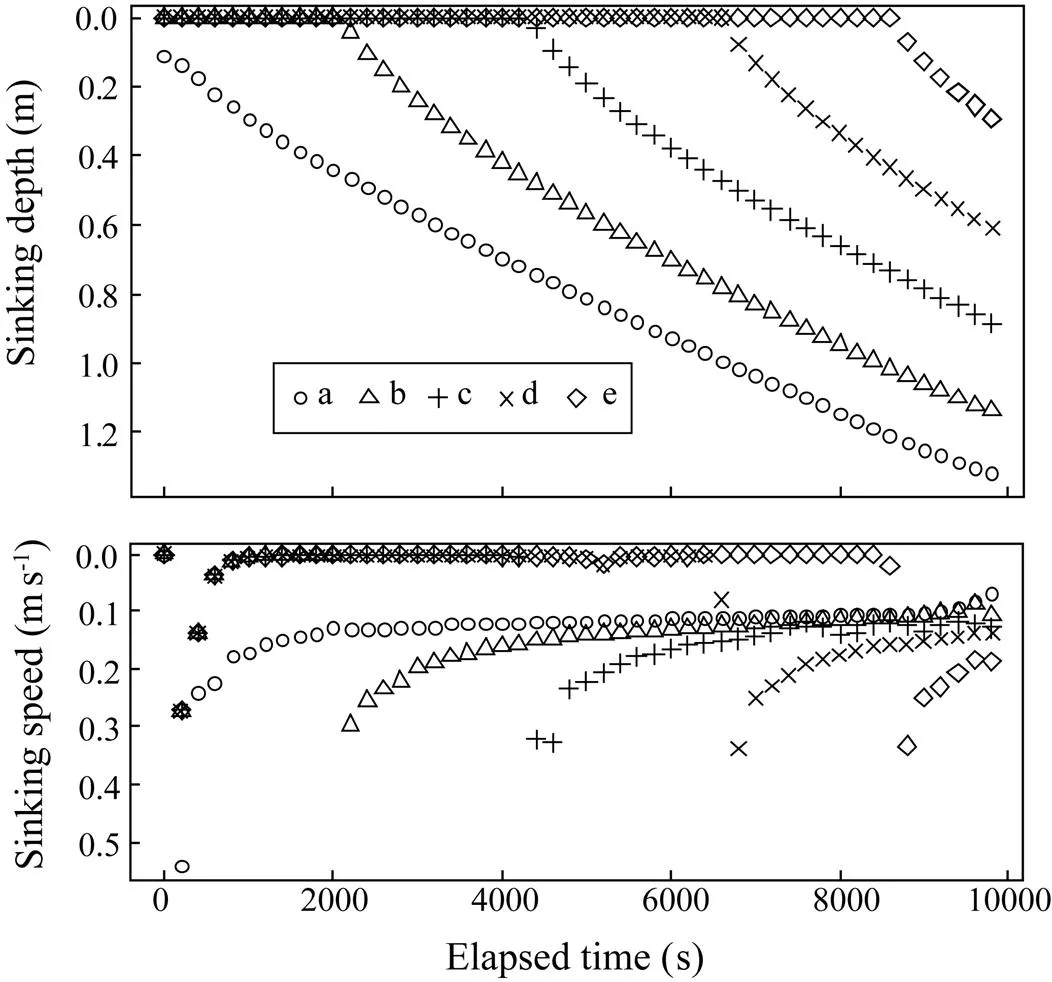
Fig.4 The variation tendency of sinking depth and speed with elapsed time for mass points at different positions on the leadline.

From the front wing end, the 3rd, 23rd, 43rd, 63rd, and 79thmass points (respectively marked as a, b, c, d, and e) of the leadline were selected in turn to analyze the sinking speed and depth of the netting at different positions (Fig.3). Fig.4 shows that mass points from a through e fell into water successively with a time step of 0.2s. Their sinking speeds gradually decreased with elapsed time and eventually stabilized at 0.14ms?1.

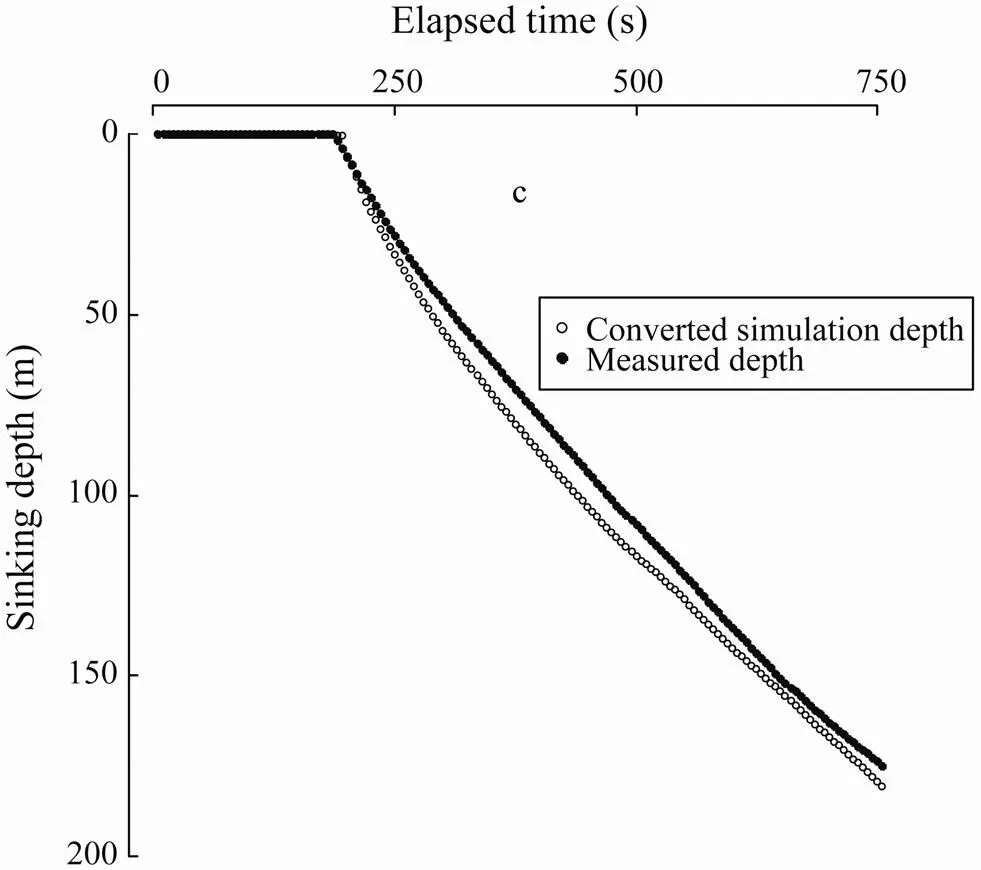
Fig.5 Comparison of sinking depth against time between simulated results and field experimental data at the middle position of the leadline.

To verify the simulation results, data were collected from field experiment when recording normal operation of a purse seine. Among the captures, we selected the operations with minimal impact of current in the fishing ground. The sinking depth was continuously logged using a depth recorder (TDR-2050, Richard Brancker Research Ltd., Canada) fixed to the middle position of the leadline, corresponding to the mass pointin the model net. The depth against time of the simulated model net was converted to compare with depth at the corresponding time of field measurement (Fig.5). The results indicate no pronounced differences between the calculated and observed values, despite that the former appeared slightly greater than the latter.

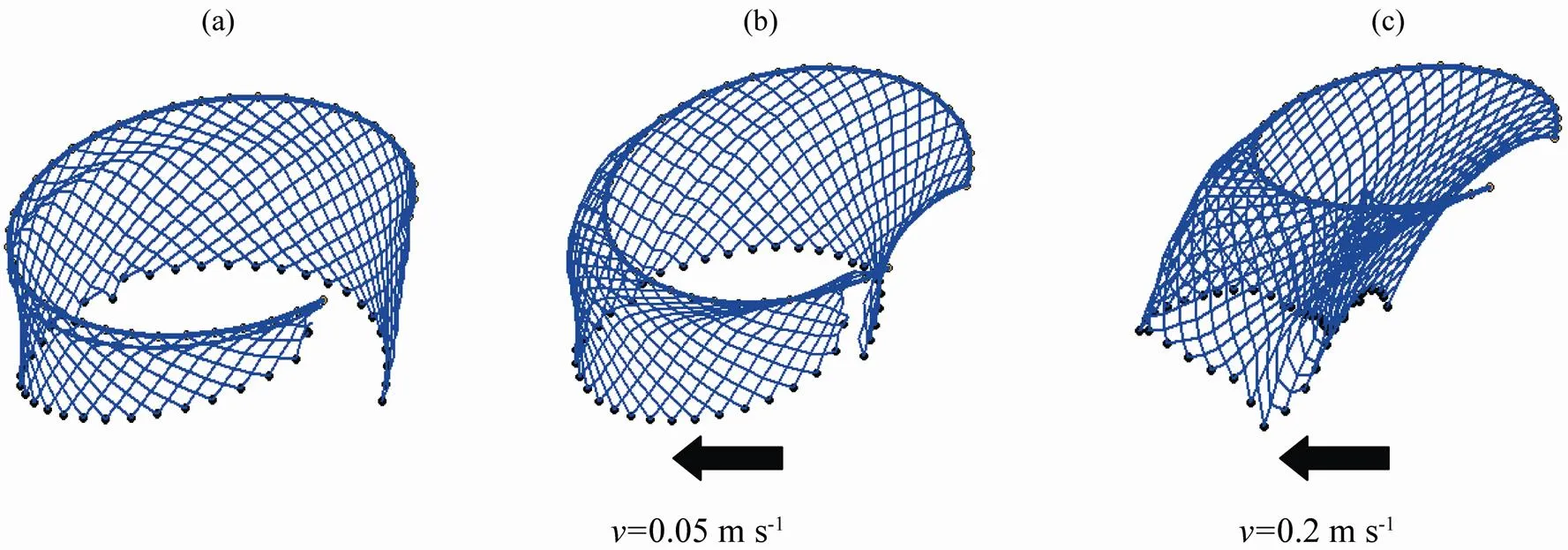
Fig.6 An equilibrium state of netting shape corresponding to different current speeds, (a) no current; (b) current speed of 0.05ms?1; and (c) current speed of 0.2ms?1.

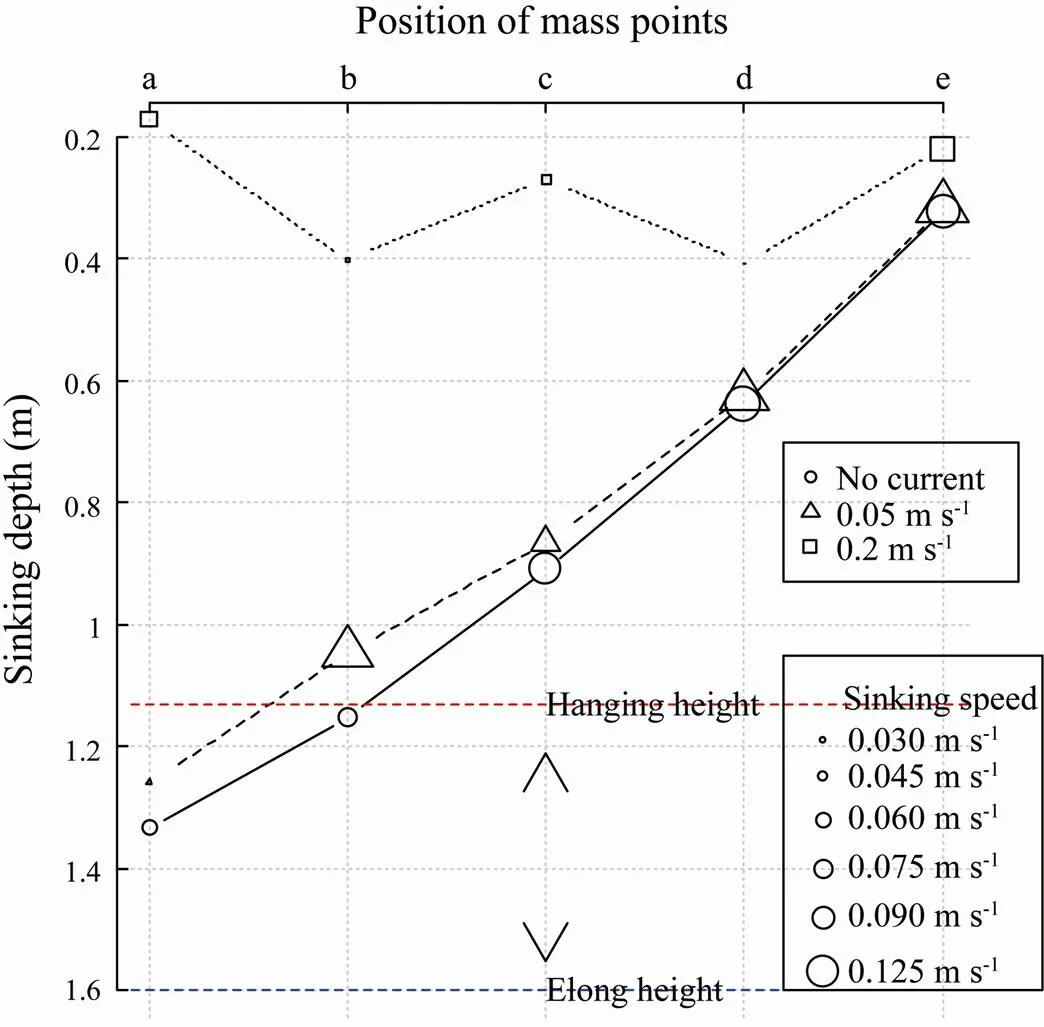
Fig.7 Operational depths corresponding to different current speeds for mass points at different positions on the leadline. Note that the size of the symbols indicates the sinking speed.

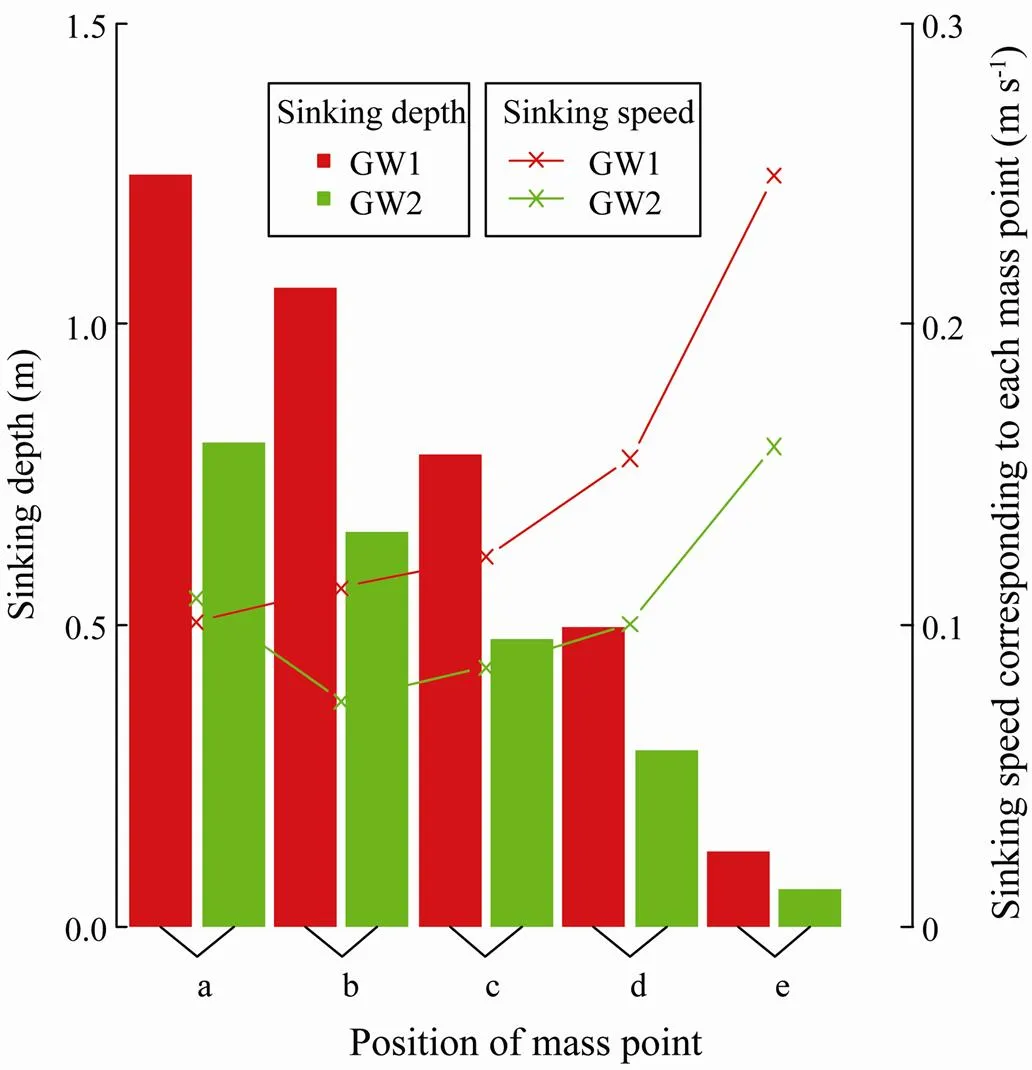
Fig.8 Sinking depths corresponding to different weights of sinkers (GW1 and GW2) for mass points at different positions on the leadline in static water.

The dimensional configurations of the purse seine are given for an equilibrium state with no current, current speed of 0.05ms?1, and current speed of 0.2ms?1(Fig.6). In water under static conditions, the net panel was stretched vertically with the sinking force. With increasing current speed, the middle part of the netting sustained a larger displacement along the direction of current. When the current speed reached 0.2ms?1, the netting underwent serious deformation as the sinkers drifted in the direction of current under the influence of hydrodynamic force.

The sinking depth at each current speed was examined in Fig.7. There was no evident difference in sinking depth between static water and flow water with a current speed of 0.05ms?1. However, the sinking depth became obviously lower at the current speed of 0.2ms?1. With different levels of sinker weight in uniform static water, GW1 obtained greater sinking depths (64%, 61%, 60%, 58%, and 48%) than GW2 (Fig.8). An overall table is given to specify the changes in sinking depth with elapsed time under different conditions of current flow (Table 1).

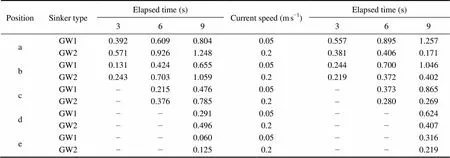
Table 1 Comparison of sinking depths corresponding to different sinker weights and current speeds with elapsed time at different measurement positions along the leadline

Note: A comparison for different sinker weights in static water (left) and a comparison for different current speeds in the uniform GW2 pattern (right).

4 Discussions

Numerical simulations are proven competent for evaluating the spatial shape and performance of purse seines underwater. Compared with other approaches, numerical simulations are particularly advantageous to observe dynamical behavior of submerged nets (Kim., 2007; Hosseini., 2011). In the present study, a mass- spring model characterized by mass points and springs was adopted to simulate the shooting process of a purse seine. However, it was almost impossible to simulate the actual fishing behavior because of the complexity of purse seine structure, the diversity of operational activities, and the variability of external environmental factors. Beginning with a simple case, a piece of rectangular plane netting was approximated as the model of a purse seine, with the aim of reflecting the properties of real gear. Relevant figures indicate that both the speed of current and the weight of sinkers significantly altered sinking depth of the model netting.

Among the parameters for the simulation, the stiffness and resistance coefficients significantly influence the shape of the netting and the solution of the motion equation. Many experiments about the interpretation of the resistance coefficients have been conducted with actual gear or in a fluid flume tank. Aarsnes. (1990) suggested that the drag and lift coefficients were related to the length and diameter of the bar and the attack angle. Tauti (1934) suggested that the hanging ratio should also be considered in the formula. Hosseini. (2011) took into account the drag coefficients as a function of attack angle and Reynolds number. However, it is hard to define the relationship expression because of the complex effects of a great many factors (Lee., 2007).

The resistance coefficient formula presented in this paper was initially introduced by Hoerner (1965), who studied the drag coefficient of a cylinder with its axis direction at an angle of inclination to the current, and treated drag force as the resultant force of frictional resistance and partial resistance of the shape. Variation in the drag coefficient is only dependent on the attack angle with a derived theoretical value. In the case of a purse seine, a higher motion speed is gained in the sinking stage, resulting in an increasing value of the Reynolds number which would affect the drag coefficient. Over the range of 200 to 600, the Reynolds number has a negligible effect on the drag coefficient while the form resistance plays a dominant role in drag force component. It is thus reasonable that the function of the drag coefficient is considered to be partly depending on the attack angle.

The great discrepancy of gravity exerted between the sinkers and the mesh bar makes the equation group a stiff system sensitive to time step. It requires a time step that is small enough to solve the stiff equation. There is a large number of knots in a purse seine net. More mass points in the simulation mean an increased calculation load and a longer computational time. A relatively large time step is thus required for such an enormous system to save computational time. However, in the case where the stiffness of twine is high, the calculation method may not be stable. We found a balance by setting a time step of 1/1000 s in the simulation to solve the conflict between calculation efficiency and accuracy. With the exclusion of a time step, a suitable numerical solution could improve the stiff problems which appear in a complicated structure requiring a rigorous convergence condition.

This study introduced an implicit predictor-corrector method to ensure the precision and stability of solutions with a large time step. Reiterative modifications via a combination of the explicit Euler method and implicit trapezoid formula not only reduced the computational period but also ensured the computational precision. Compared with the explicit Euler method, the corrected formula achieved results with increased accuracy. Unlike the implicit Euler method that needs repetitious solutions and judgments of the truncation of iteration, our method achieves an adequate approximation with a minimum of two iterations for the correction process.

By comparing the simulated and measured results, the variance for the middle part of the netting was considered coincident, similar to the results from other studies (Kim., 2007; Hosseini., 2011). As mentioned in those studies, the incidence of the shadowing effect of the mesh bars reduces the current speed, resulting in changes in the drag. Additionally, the tension of the purse line in actual fishing operation tends to decrease the sinking speed, which was not considered in our simulation.

The variations in sinking depth at different positions along the leadline accord with a normal rule where the sinking depth decreases successively from bunt to back wing and the sinking speed decreases with elapsed time. There is considerable distortion of netting in the case of strong current owing to the movement of the netting wall under the action of current forces. There is no comparable observation with other studies because of different parameters used in our simulation. Moreover, the netting dropped at an operational depth between stretched depth and hanging depth. In general, the seine rarely achieves the fully stretched height under the effects of pursing speed and other relevant factors. The speed of the current plays a vital role in regulating the net shape and sinking performance. Fridman (1973) concluded that sinking speed could be reduced by 1/3 to 1/2 at a current speed of 0.2–0.3ms?1, comparable to our results.

The model introduced in this study merely provides a motion of potential as a method for visualization of a purse seine. Some other relevant variables that appear in actual fishing operation are not taken into account in the input data of the simulation. Further study is needed to imitate fishing conditions more closely, using parameters such as shooting speed, pursing speed, purse line tension, and current profile.

Acknowledgements

This study was financially supported by the National High Technology Research and Development Program of China (No. 2012AA092302); the Specialized Research Fund for the Doctoral Program of Higher Education (No. 20103104120006), and the Project of First-class Disciplines Shanghai Universities: Eco-Friendly Fishing Gear and Fishing Methods in the Field of Fisheries Science (B-5005-12-0001-4C). The authors would like to thank Dr. Natalie Jones from University of Massachusetts, Dartmouth, and Dr. Jason Boucher from Shanghai Ocean University (Post-Doctor Research Program) for language editing and improvement of the manuscript.

Aarsnes, J. V., Rudi, H., and Loland, G., 1990. Current forces on cage, net deflection., 137-152.

Fridman, A. L., 1973. Theory and design of commercial fishing gear. Israel Program for Scientific Translation. Jerusalem.

Hoernor, S. F., 1965.. Brick Town, New York, 1-455.

Hosseini, S. A., Lee, C. W., Kim, H. S., Lee, J. H., and Lee, G. H., 2011. The sinking performance of the tuna purse seine gear with large-meshed panels using numerical method., 77: 503-520.

Hu, F. X., Matuda, K., Tokai, T., and Haruyuki, K., 1995. Dynamic analysis of midwater trawl system by a two-dimen- sional lumped mass method., 61: 229-233.

Huang, C. C., Tang, H. J., and Liu, J. Y., 2006. Dynamical analysis of net cage structures for marine aquaculture: Numerical simulation and model testing., 35: 258-270.

Kim, H. Y., Lee, C. W., Shin, J. K., Kim, H. S., Cha, B. J., and Lee, G. H., 2007. Dynamic simulation of the behavior of purse seine gear and sea-trial verification., 88: 109-119.

Kim, S. J., 2004. An analysis of the sinking resistance of a purse seine. (2). The case of a model purse seine with different netting materials and sinkers., 40 (1): 29-36 (in Korean with English abstract).

Kim, Y. H., and Park, M. C., 2009. The simulation of the geometry of a tuna purse seine under current and drift of purse seiner., 36: 1080-1088.

Lee, C. W., and Cha, B. J., 2002. Dynamic simulation of a midwater trawl system’s behavior., 68: 1865- 1868.

Lee, C. W., Jang, C. S., Kim, M. S., Shin, H. Y., and Kim, I. J., 1998. Measurements of midwater trawl system and dynamic characteristics., 34 (3): 294-301 (in Korean with English abstract).

Lee, C. W., Lee, J. H., Cha, B. J., Kim, H. Y., and Lee, J. H., 2005a. Physical modeling for underwater flexible systems dynamic simulation., 32: 331-347.

Lee, J. H., Lee, C. W., and Cha, B. J., 2005b. Dynamic simulation of tuna longline gear using numerical methods., 71: 1287-1294.

Lee, M. K., Lee, C. W., and Song, D. H., 2007. Experiments on hydrodynamic coefficients of netting in relation to mesh grouping. DEMAT’07,, 5: 35-44.

Li, Y. C., Zhao, Y. P., Gui, F. K., and Teng, B., 2006. Numerical simulation of the hydrodynamic behavior of submerged plane nets in current., 33: 2352-2368.

Liu, D. C., Nashimoto, K., and Yamamoto, K., 1984. Configuration of lead line of purse seine during pursing., 35 (4): 234-242 (in Japanese with English abstract).

Machii, T., and Nose, Y., 1992. Mechanical properties of a rectangular purse seine in ideal conditions., 14: 261-271.

Niedzwiedz, G., and Hopp, M., 1998. Rope and net calculations applied to problems in marine engineering and fisheries research., 46 (2): 125- 138.

Paschen, N. G., and Winkel, H. J., 2002. Wind tunnel tests for fishing gear development-methods and limits. DEMAT’01., 2: 29-41.

Song, L. M., Zhang, Z., Yuan, J. T., and Li, Y. W., 2011. Numeric modeling of a pelagic longline based on minimum potential energy principle., 18 (5): 1170-1178 (in Chinese with English abstract).

Tauti, M., 1934. A relation between experiments on model and on full scale of fishing net., 3 (4): 171-177 (in Japanese with English abstract).

Wan, R., Cui, J. H., Song, X. F., Tang, Y. L., Zhao, F. F., and Huang, L. Y., 2005. A numerical model for predicting the fishing operation status of tuna longlines., 29 (2): 238-245 (in Chinese with English abstract).

Wan, R., Hu, F. X., Tokai, T., and Matuda, K., 2002. A method for analyzing the static response of submerged rope systems based on a finite element method., 68 (1): 65-70.

Xu, L. X., Lan, G. C., Ye, X. C., and Wang, M. F., 2011a. Effect of the leadline weight and net setting speed on sinking speed of the tuna purse seine., 35 (10): 1563-1571 (in Chinese with English abstract).

Xu, L. X., Wang, M. F., Ye, X. C., and Lan, G. C., 2011b. Measurement and analysis of sinking characteristics of tuna purse seine., 18 (5): 1161- 1169 (in Chinese with English abstract).

Yoshihara, T., 1951. Distribution of fishes caught by the long line-II. Vertical distribution., 16: 370-374 (in Japanese with English abstract).

Zhao, Y. P., Li, Y. C., Gui, F. K., and Dong, G. H., 2007. Numerical simulation of the effects of weight system on the hydrodynamic behavior of 3-D net of gravity cage in current., 19 (4): 442-452.

Zhao, Y. P., Xu, T. J., Dong, G. H., and Li, Y. C., 2010. Numerical simulation of a submerged gravity cage with the frame anchor system in irregular waves., 22 (5): 433-437.

(Edited by Qiu Yantao)

DOI 10.1007/s11802-015-2384-8

ISSN 1672-5182, 2015 14 (1): 135-142

(May 2, 2013; revised August 18, 2013; accepted May 13, 2014)

. Tel: 0086-21-61900301 E-mail: lxxu@shou.edu.cn

? Ocean University of China, Science Press and Spring-Verlag Berlin Heidelberg 2015