Elliptic Systems with a Partially Sublinear LocalTerm

Yongtao Jing and Zhaoli Liu

School of Mathematical Sciences,Capital Normal University,Beijing 100048,P.R.China

Elliptic Systems with a Partially Sublinear LocalTerm

Yongtao Jing and Zhaoli Liu?

School of Mathematical Sciences,Capital Normal University,Beijing 100048,P.R.China

.Let 1＜p＜2.Under some assumptions onV,K,existence of infinitely many solutions(u,φ)∈H1(R3)×D1,2(R3)is proved for the Schr¨odinger-Poisson system(

as well as for the Klein-Gordon-Maxwell system

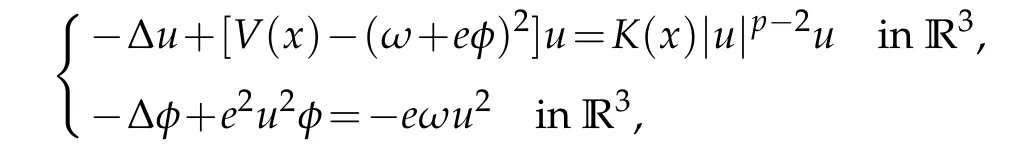
whereω,e＞0.This is in sharp contrastto D’Aprile and Mugnai’snon-existence results.

AMS subject classifications:35A15,35J50

Schr¨odinger-Poisson system,Klein-Gordon-Maxwell system,infinitely many solutions.

1 Introduction and main results

In this paper,we study existence ofinfinitely many solutions(u,φ)∈H1(R3)×D1,2(R3)to the Schr¨odinger-Poisson system

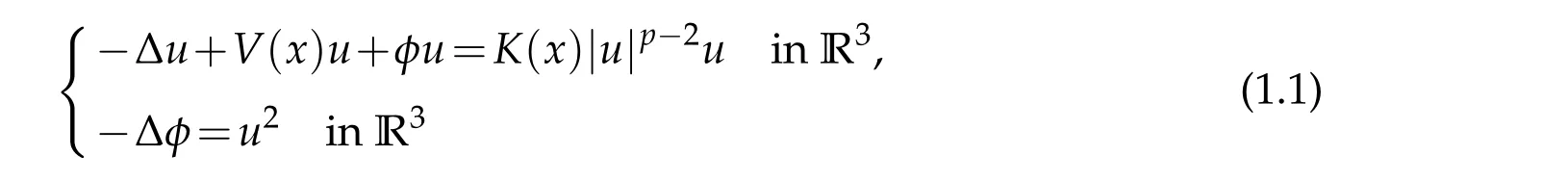
for 1＜p＜2.

This system has a wide background in physics.It is reduced from the Hartree-Fock equations by a mean field approximation([9,10]).It also describes the Klein-Gordon orSchr¨odinger fields interacting with an electromagnetic field([3]).The related Thomas-Fermi-von Weizs¨acker model describes the ground states of nonrelativistic atoms and molecules in the quantum mechanics([1]).

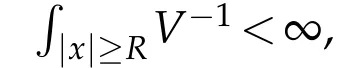
We will consider the more general system

To state our main result,we need the following assumptions:

(V)V∈C(R3,R),infV＞?∞,there isR＞0 such that

(F)There exist positive numbersδandcandp∈(1,2)such thatf∈C(R3×[?δ,δ],R),f(x,t)is odd int,

and there existx0∈R3andr＞0 such that

Theorem 1.1.Under(V)and(F),(1.2)has infinitely many nontrivial solutions in H1(R3)×D1,2(R3).

Assumption(V)makesVlook like a well-shaped potential.Note that the nonlinear termf(x,t)in assumption(F)is defined only for|t|≤δ.Accordingly,theL∞(R3)norm ofuin(u,φ),the solution we will obtain,will have to be less thanδ.

From(V)and(F),it is without loss of any generality to assume further in Theorem 1.1 that

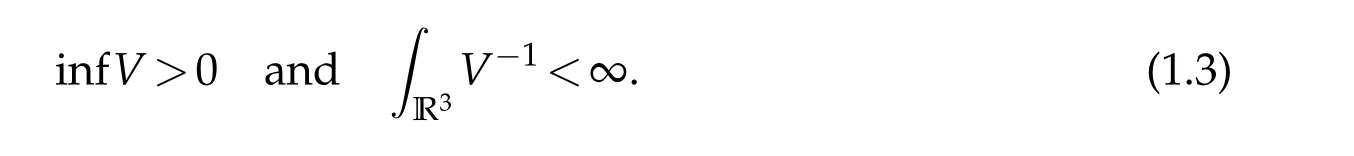
This can be seen by adding ?νuto both sides of the first equation in(1.2),whereνis any number such thatν＜infV.The assumption that infV≥1 and ∫R3V?1＜∞was used in[6]in dealing with sublinear Schr¨odinger equations.

The following corollary is a direct consequence of Theorem 1.1.

Corollary 1.1.Under(V),if K∈C(R3,R),K is bounded,and there exists x0∈R3such that K(x0)＞0,then(1.1)has infinitely many nontrivial solutions in H1(R3)×D1,2(R3).

Corollary 1.1 is in sharp contrast to the non-existence result for(1.1)in[2]which asserts that(1.1)has no nontrivial solution ifV≡1≡K.

A system similar to(1.1)is the following system of coupled Klein-Gordon-Maxwell equations

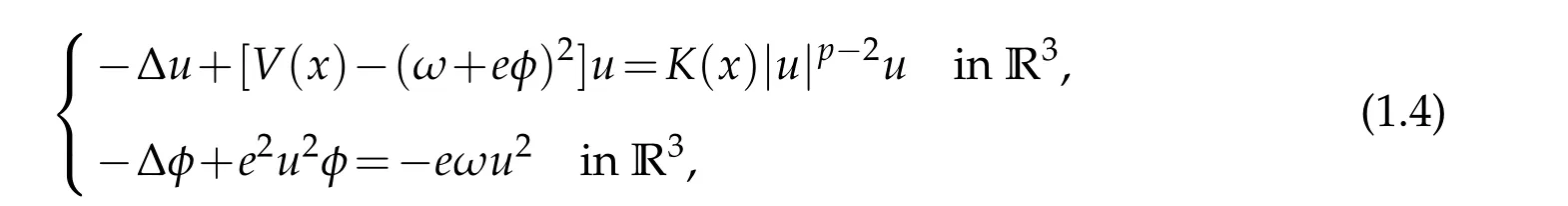
where 1＜p＜2 andω,e＞0.The caseV≡m2andK≡1 is studied in[2],where one can find the physical meaning of the positive constantsm,e,ωand the physical background of(1.4).

Our second main result is for the more general system

Theorem 1.2.Under(V)and(F),(1.5)has infinitely many nontrivial solutions in H1(R3)×D1,2(R3).

As remarked above for Theorem 1.1,by adding(?ν+ω2)uto both sides of the first equation in(1.5)whereνis any number such thatν＜infV,we can assume in addition in Theorem 1.2 that

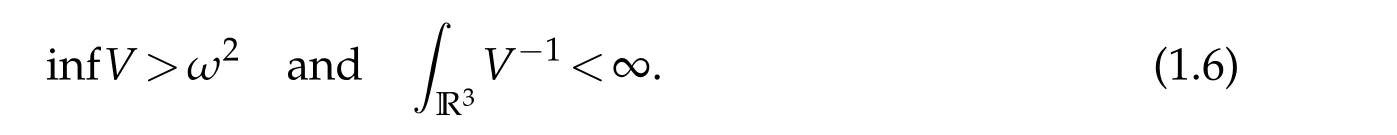
The following corollary is a direct consequence of Theorem 1.2.

Corollary 1.2.Under(V),if K∈C(R3,R),K is bounded,and there exists x0∈R3such that K(x0)＞0,then(1.4)has infinitely many nontrivial solutions in H1(R3)×D1,2(R3).

It is proved in[2]that ifV≡m2,K≡1,andm,e,ω＞0 then(1.4)has no nontrivial solution.So Corollary 1.2 provides a sharp contrast.

The assumption∫R3V?1＜∞,which is a crucial assumption in Theorems 1.1 and 1.2 according to D’Aprile and Mugnai’s non-existence results,will only provide compactness in our arguments.This assumption can be replaced with a similar assumption onKwhen considering(1.1)and(1.4),as illustrated in the following two theorems.

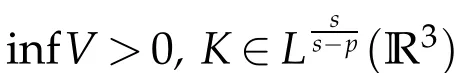
Theorem 1.4.Assume that V,K∈C(R3,R),infV＞ω2,K∈Lss?p(R3)for some2≤s≤6,and there exists x0∈R3such that K(x0)＞0,then(1.4)has infinitely many nontrivial solutions in H1(R3)×D1,2(R3).

Some preparations will be given in Section 2.Theorem 1.1 will be proved in Section 3 and Theorem 1.2 will be proved in Section 4.We will prove Theorems 1.3 and 1.4 in Sections 5 and 6 respectively.In this paper,CandCjare positive constants which may be variant even in the same line.

2 Preliminaries

Consider the modified system

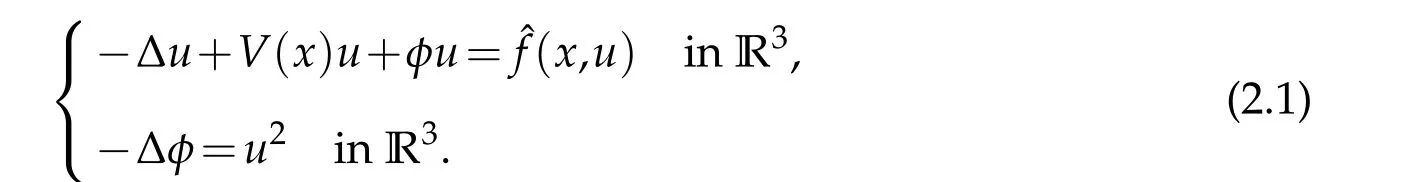
Any solution(u,φ)∈H1(R3)×D1,2(R3)of(2.1)satisfying ‖u‖L∞(R3)＜δis clearly a solution of(1.2).Therefore it suffices to find infinitely many solutions(un,φn)of(2.1)with‖un‖L∞(R3)→0.The same remark holds for(1.5)and its modification

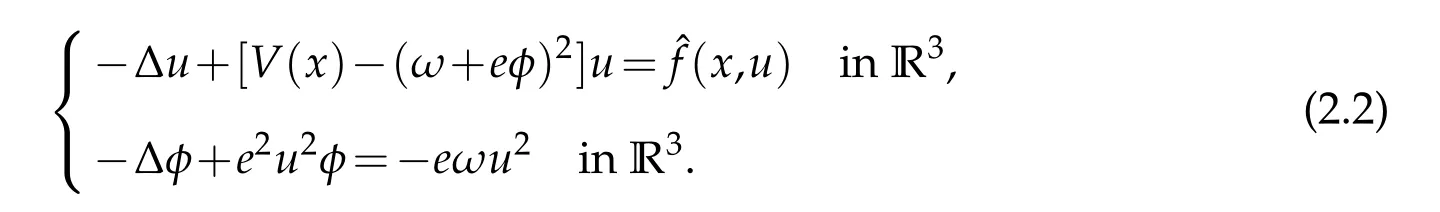
We will work in the Banach spaceEdefined to be

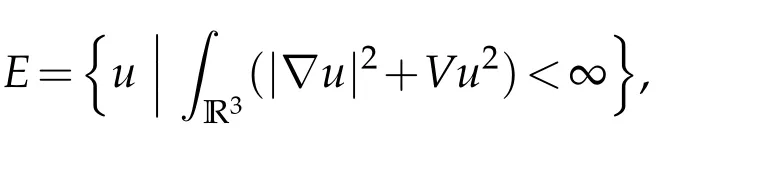
in which the norm is

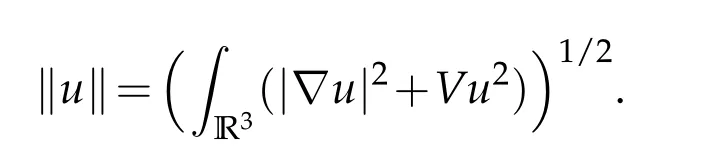
From infV＞0 andR3V?1＜∞,it can be deduced that

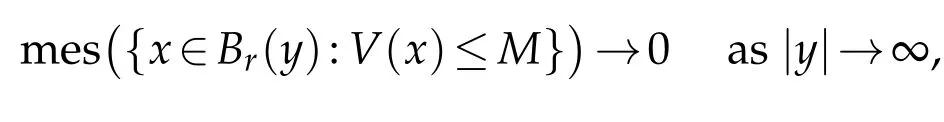
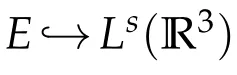
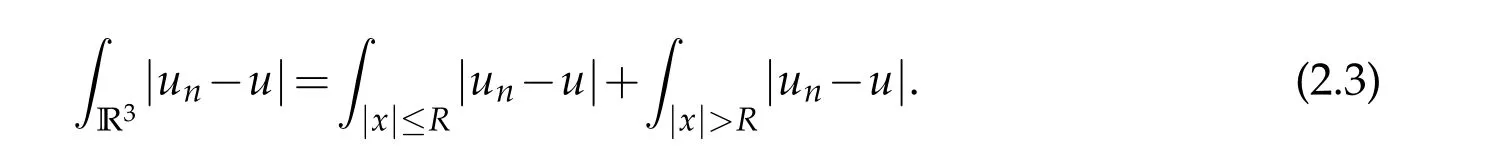
Use the H¨older inequality to see that

SinceE■→L12/5(R3),it follows from the Riesz representation theorem that for anyu∈Ethere is a uniqueφ=φu∈D1,2(R3)such that the second equation in(2.1)is solved.Thisφuhas an explicit representation

We insert thisφuinto the first equation in(2.1).Then(2.1)can be rewritten as

Solutions of(2.6)will be found via critical point theory.Set

The functional associated with(2.6)is the functionalJdefined to be

foru∈E.

To convert(2.2)to a single equation,we recall the following result from[2].

The functional associated with(2.9)is

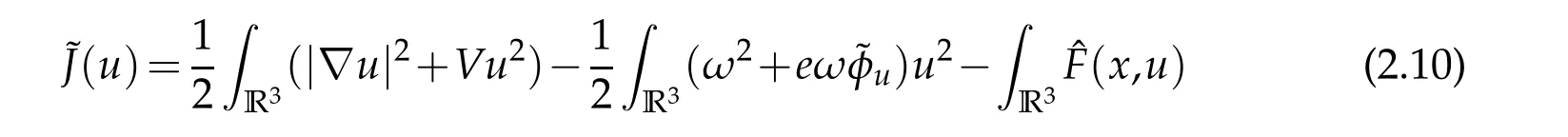
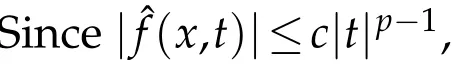
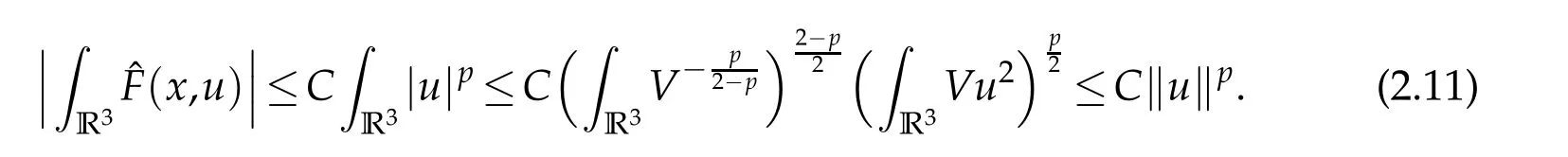
Theorem B.Under the same assumptions as in Theorem A,Φhas a sequence of nonzero critical points converging to0.

3 Proof of Theorem 1.1

To prove Theorem 1.1,we will apply Theorem B to prove thatJhas a sequence of critical points converging to 0 inEand then we will prove that this sequence also converges to 0 inL∞(R3).

We first verify the assumptions of Theorems A.Clearly,Jis aC1functional,Jis even and bounded below,andJ(0)=0.

Lemma3.1.J satisfies the(PS)condition.That is,any sequence{un}such that J(un)is bounded and J′(un)→0has a converging subsequence.

Proof.SinceJ(un)is bounded,it is clear that{un}is bounded.Therefore,we may extract a subsequence,still denoted by{un},such that

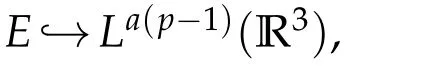
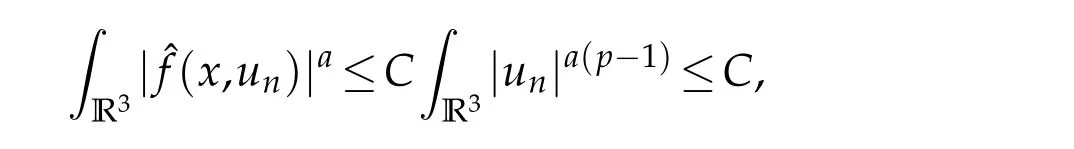
we may assume that

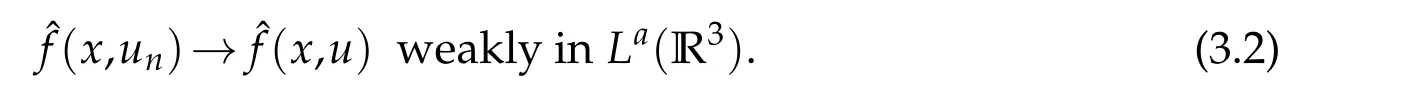
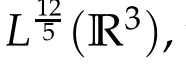
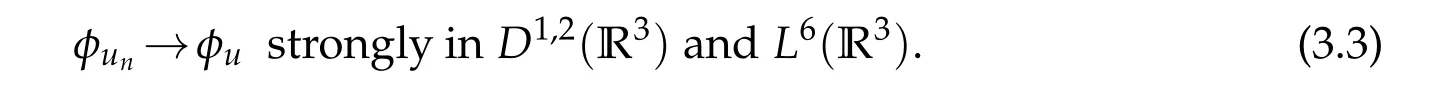
For anyv∈E,taking limit asn→∞in

we use(3.1a)-(3.3)to see that

Then it is easy to see that‖un?u‖→0.

Lemma 3.2.For any k∈N,there exist a k-dimensional subspace Ekof E and ρk＞0such that

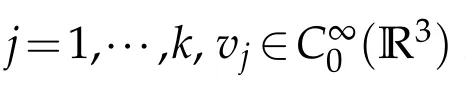
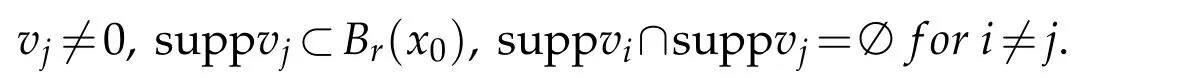
LetEk=span{v1,v2,···,vk}.Choose positive numbersξandτsuch that

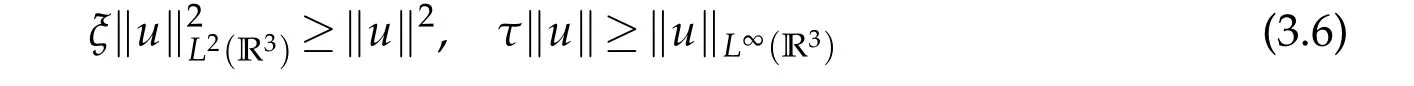
for anyu∈Ek.From assumption(F),we findμ＞0 such that

Letu∈Ekand ‖u‖=1.For 0＜ρ＜μ/τ,we have

To obtain(3.5)it suffices to chooseρ=ρksmall enough.

Proof of Theorem 1.1.According to Lemmas 3.1 and 3.2,all the assumptions in Theorem A are satisfied.By Theorem B,Jhas a sequence of critical points{un}converging to 0 inE.It suffices to prove that‖un‖L∞(R3)→0.

Sinceunsolves equation(2.6),we have

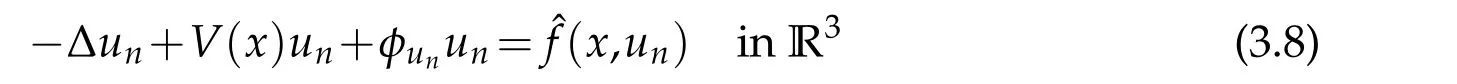
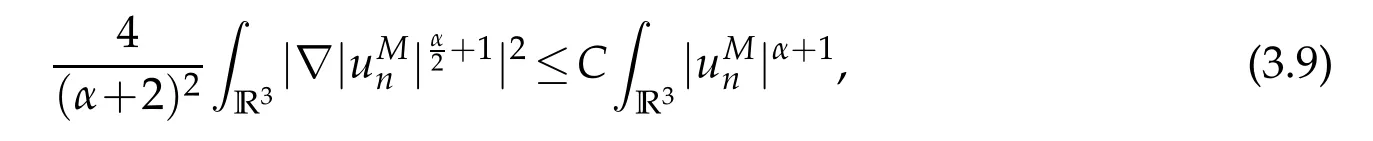
which together with the Sobolev inequality yields

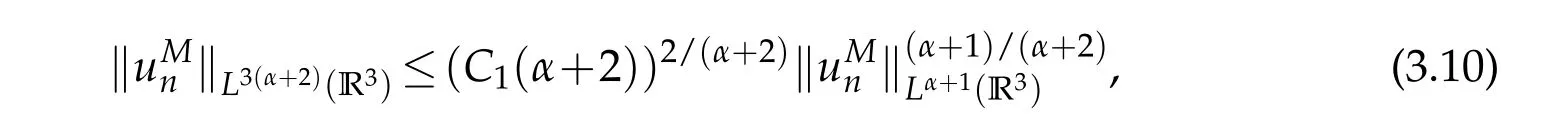
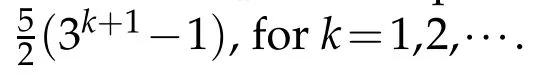
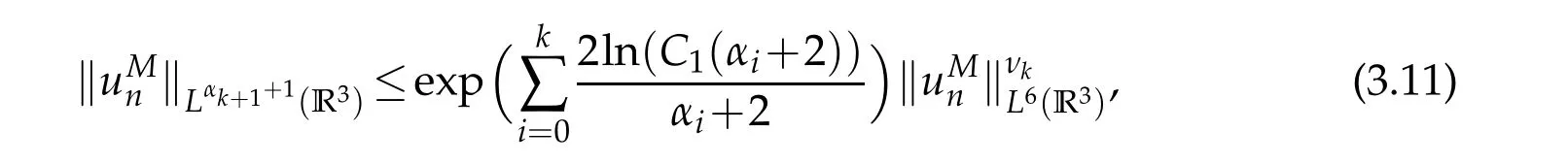
4 Proof of Theorem 1.2

To prove Theorem 1.2,we will apply Theorem B to prove that?Jhas a sequence of critical points converging to 0 inEand then we will prove that this sequence also converges to 0 inL∞(R3).

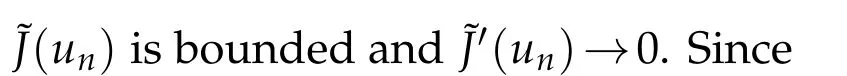
Choosea≥6/5 such that 1＜a(p?1)＜6.Then

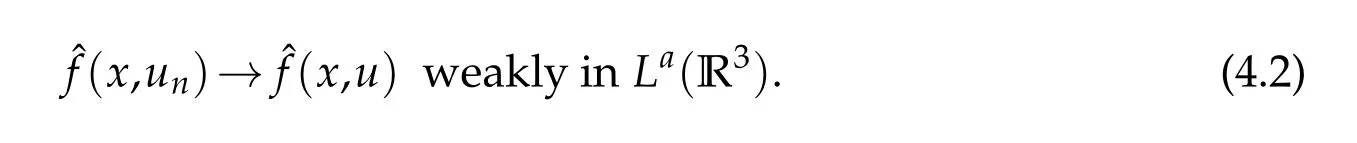
From the equations

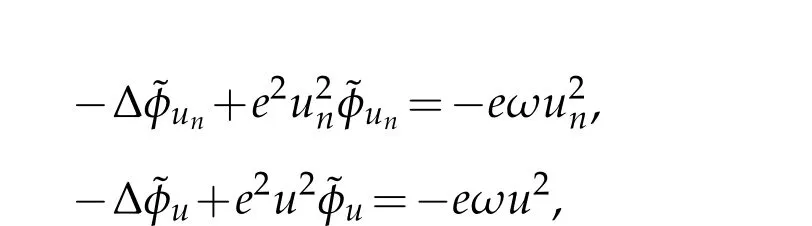
we have

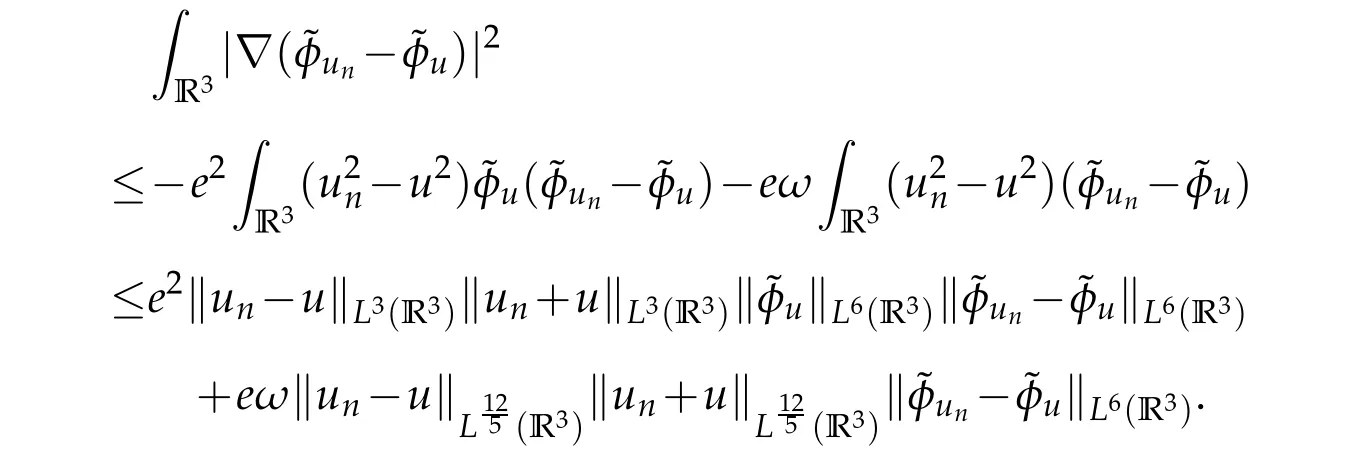
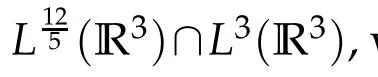
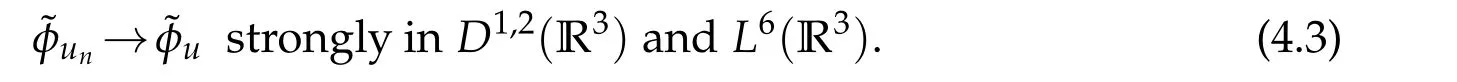
From Lemma 2.2,forv∈E,we see that

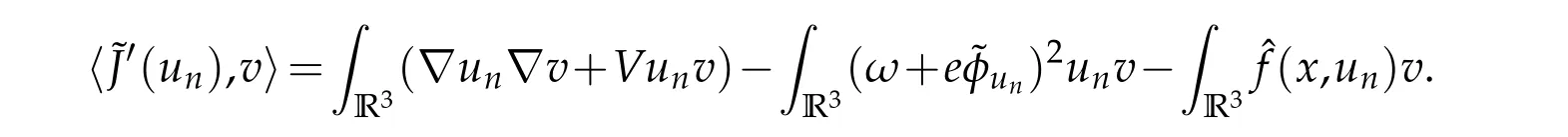
Lettingn→∞and using(4.1)-(4.3)to conclude

Then it is easy to see that‖un?u‖→0.

Lemma 4.2.For any k∈N,there exist a k-dimensional subspace Ekof E and ρk＞0such that

Proof.Since,by Lemma 2.2,

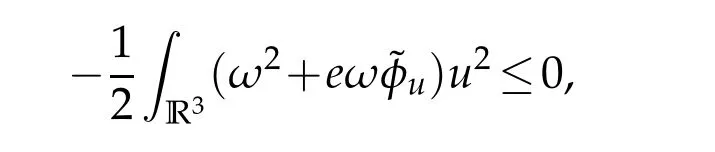
we have

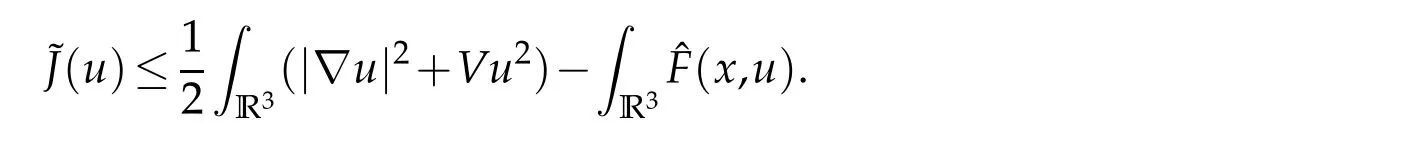
The proof is then the same as that of Lemma 3.2.

Proof of Theorem 1.2.We use Lemmas 4.1 and 4.2 and the same argument as in the proof of Theorem 1.1.

5 Proof of Theorem 1.3

The functional associated with(1.1)is the functionalIdefined to be

foru∈E.

In order to prove Theorem 1.3,we will apply Theorem A to prove thatIhas a sequence of negative critical values converging to 0.

We first verify the assumptions of Theorems A.Clearly,Iis aC1functional,Iis even,andI(0)=0.

Lemma 5.1.I is coercive and bounded below.

Proof.By the H¨older inequality andφu≥0,we have

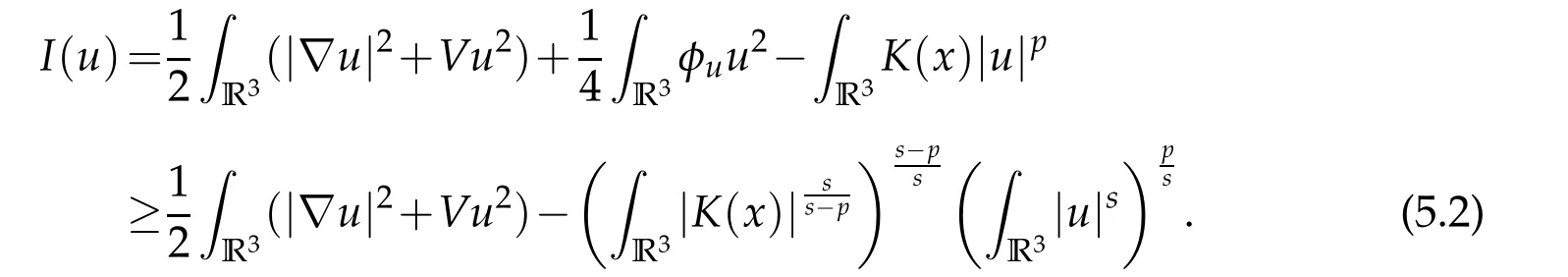
The conclusion follows since 1＜p＜2.

Lemma 5.2.I satisfies the(PS)condition.

Proof.Let{un}be a sequence such thatI(un)is bounded andI′(un)→ 0.SinceI(un)is bounded,it follows from Lemma 5.5 that{un}is bounded.Therefore,passing to a subsequence,we assume that

ByI′(un)→0 andun→uweakly inE,we have

We writeI1as

Using[5,Theorem 9.8],we have

The H¨older inequality implies

Combining the last two inequalities we conclude that

ForI2,by the H¨older inequality,for anyR＞0,we have

Givenε＞0,we fixR＞0 such that

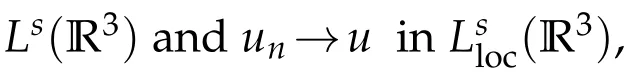
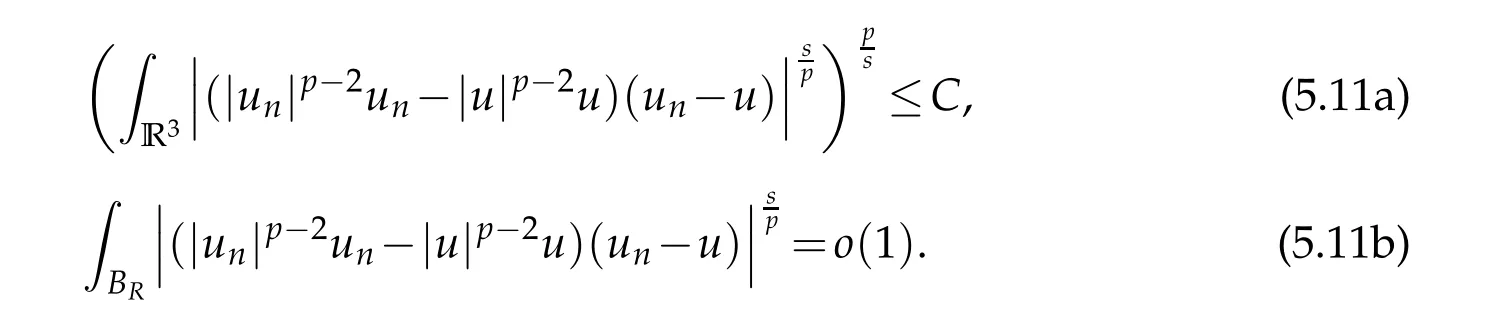
Therefore,

Lettingn→∞ andε→0,we see that

From(5.5),(5.9),and(5.13),we conclude that‖un?u‖→0.

Lemma 5.3.For any k∈N,there exist a k-dimensional subspace Ekof E and ρk＞0such that

Proof.Chooseδ,r＞0 such thatK(x)＞δinBr(x0).DefineEkas in the proof of Lemma 3.2.

Letu∈Ekand ‖u‖=1.Forρ＞0,we have

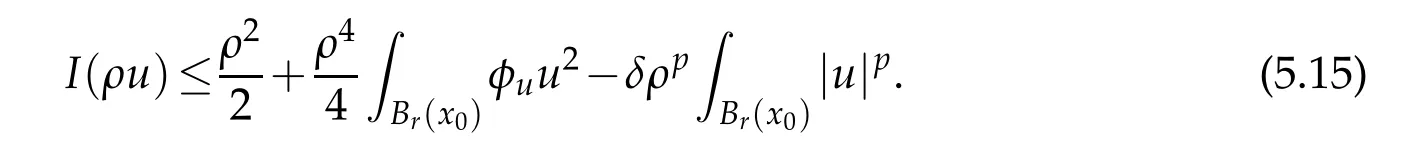
Since 1＜p＜2,it suffices to chooseρ=ρksmall enough.

Proof of Theorem 1.3.Use the above three lemmas and Theorem A.

6 Proof of Theorem 1.4

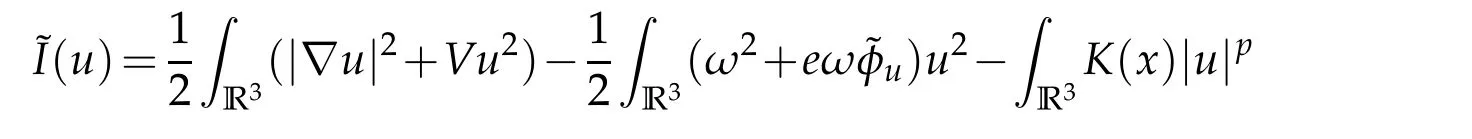
foru∈E.

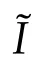
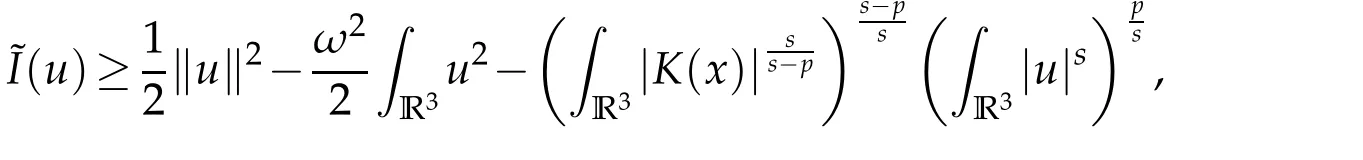
which together with the assumption infV＞ω2and the Sobolev inequality yields

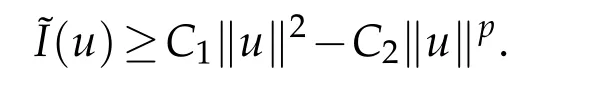
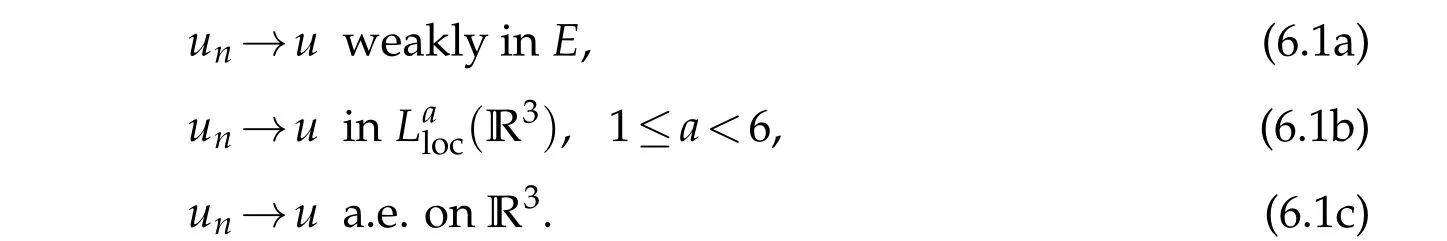
From the equation

we have

Write the second integral on the right side as

For anyR＞0,the H¨older inequality implies

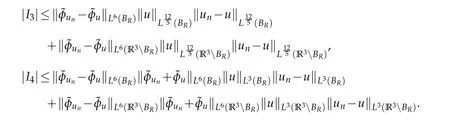
Lemma 6.3.For any k∈N,there exist a k-dimensional subspace Ekof E and ρk＞0such that

Proof.Note that

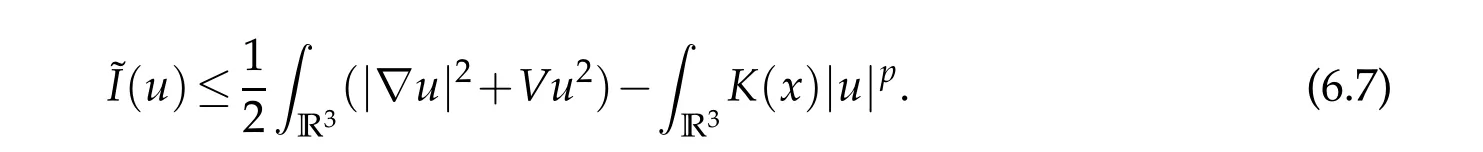
The proof of Lemma 5.3 works here.

Proof of Theorem 1.4.This is a consequence of the above three lemmas and Theorem A.

Acknowledgments

The authors are supported by NSFC(11271265,11331010)and BCMIIS.

[1]R.Benguria,H.Brezis,and E.-H.Lieb.The Thomas-Fermi-von Weizs¨acker theory of atoms and molecules.Comm.Math.Phys.,79:167-180,1981.

[2]T.D’Aprile and D.Mugnai.Non-existence results for the coupled Klein-Gordon-Maxwell equations.Adv.Nonlinear Stud.,4:307-322,2004.

[3]T.D’Aprile and D.Mugnai.Solitary waves for nonlinear Klein-Gordon-Maxwell and Schr¨odinger-Maxwell equations.Proc.Royal Soc.Edinb.,134A:893-906,2004.

[4]V.Kondrat’ev and M.Shubin.Discreteness of spectrum for the Schr¨odinger operators on manifolds of bounded geometry.Operator Theory:Advances and Applications,110:185-226,1999.

[5]E.Lieb and M.Loss.Analysis,Graduate Studies in Mathematics.AMS,14,1997.

[6]Z.L.Liu and Z.-Q.Wang.Schr¨odinger equations with concave and convex nonlinearities.Z.Angew.Math.Phys.,56:609-629,2005.

[7]Z.L.Liu and Z.-Q.Wang.On Clark’s theorem and its applications to partially sublinear problems.Ann.Inst.H.Poincare Anal.Non-lineaire,32:1015-1037,2015.

[8]A.M.Molchanov.On the discreteness of the spectrum conditions for self-adjoint differential equations of the second order(in Russian).Trudy Mosk.Matem.Obshchestva,2:169-199,1953.

[9]D.Ruiz.The Schr¨odinger-Poisson equation under the effectofa nonlinear localterm.J.Functional Analysis,237:655-674,2006.

[10]D.Ruiz.On the Schr¨odinger-Poisson-Slater system:behavior of minimizers,radial and nonradial cases.Arch.Rat.Mech.Anal.,198:349-368,2010.

9 April,2015;Accepted 13 May,2015

?Corresponding author.Email address:zliu@cnu.edu.cn(Z.-L.Liu),jing@cnu.edu.cn(Y.-T.Jing)