Mengkun Zhuand Xinzhong Huang

SchoolofMathematicalScience,HuaqiaoUniversity,Quanzhou362021,Fujian Province,P.R.China.

The Distortion Theorems for Harmonic Mappings with Negative Coefficient Analytic Parts

Mengkun Zhu?and Xinzhong Huang

SchoolofMathematicalScience,HuaqiaoUniversity,Quanzhou362021,Fujian Province,P.R.China.

.Some sharp estimates for coefficients,distortion and the growth order are obtained for harmonic mappingsf∈TLαHwhich are locally univalent harmonic mappings in the unit diskD={z:|z|＜ 1}.Moreover,denoting the subclassTSαHof the normalized univalent harmonic mappings,we also estimate the growth of|f|,f∈TSαH,and their covering theorems.

AMS subject classifications:30D15,30D99

Harmonic mapping,coefficient estimate,distortion theorem,covering problem.

1 Introduction

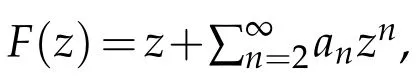
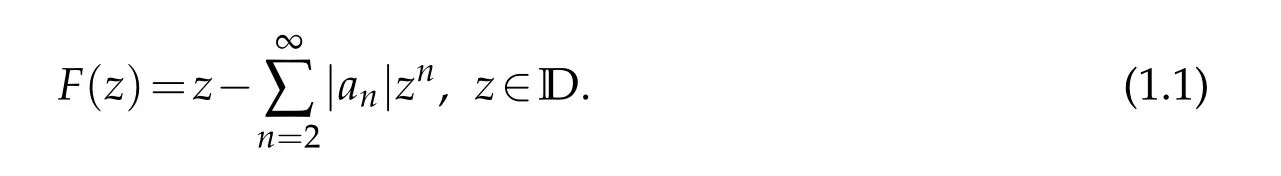
A complex-valued harmonic functionfin the unit diskDhas a canonical decomposition

wherehandgare analytic inDwithg(0)=0.Usually,we callhthe analytic part offandgthe co-analytic part off.A complete and elegant account of the theory of planar harmonic mappings is given in Duren,s monograph[1].

In[2],Ikkei Hotta and Andrzej Michalski denoted the classLHof all normalized locally univalent and sense-preserving harmonic functions in the unit disk withh(0)=g(0)=h′(0)?1=0.Which means every functionf∈LHis uniquely determined by coefficients of the following power series expansions

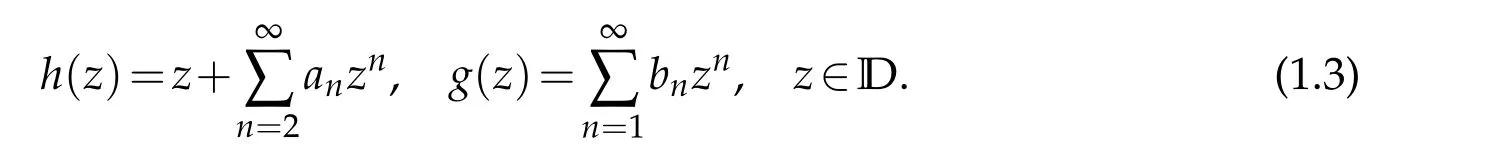
wherean,bn∈C,n=2,3,4,...Clunie and Sheil-small introduced in[3]the classSHof all normalized univalent harmonic mappings inD,obviously,SH?LH.

Lewy[4]proved that a necessary and sufficient condition forfto be locally univalent and sense-preserving inDisJf(z)＞0,where

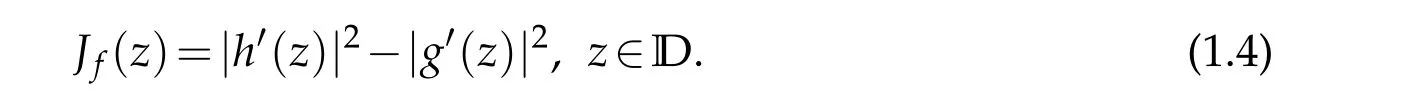
To such a functionf,not identically constant,let

thenω(z)is analytic inDwith|ω(z)|＜ 1,it is called the second complex dilatation off.

In[5],Silverman investigated the subclass ofTwhich denoted byT?(β),starlike of orderβ(0≤β＜1).That is,a functionF(z)∈T?(β)if Re{zF′(z)/F(z)}＞β,z∈D.It was proved in[5]that

Corollary 1.1.

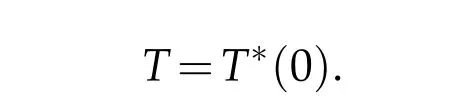
In[7-8],Dominika Klimek and Andrzej Michalski studied the cases when the analytic partshis the identity mapping or a convex mapping,respectively.The paper[2]was devoted to the case when the analytichis a starlike analytic mapping.In[9],Qin Deng got sharp results concerning coefficient estimate,distortion theorems and covering theorems for functions inT.The main idea of this paper is to characterize the subclasses ofLHandSHwhenh∈T.

In order to establish our main results,we need the following theorems and lemmas.

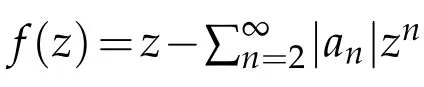
Lemma 1.1.([10])If f(z)=a0+a1z+...+anzn+...is analytic and|f(z)|≤1onD,then

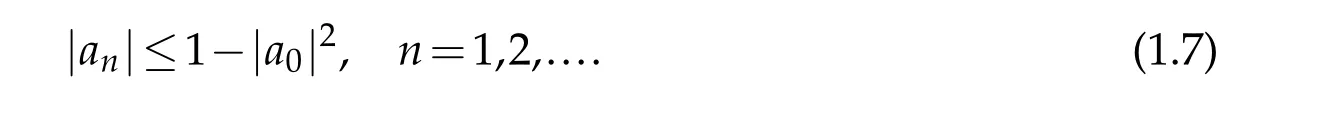
Theorem 1.2.([8])If f∈T,then

with equality for

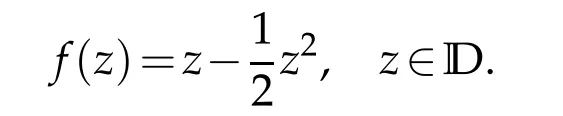
Theorem 1.3.([8])If f∈T,then

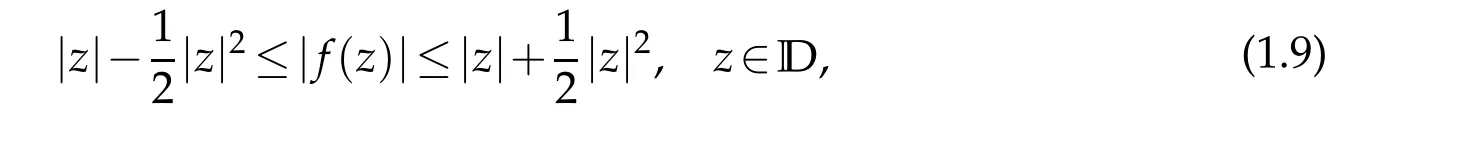
with equality for

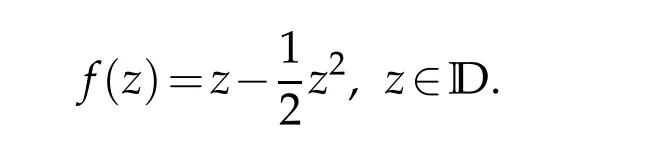
2 Main results and their proofs

Similar with the papers[2,7,8]and[12],we consider the following function sets.Definition 2.1.Forα∈[0,1),let

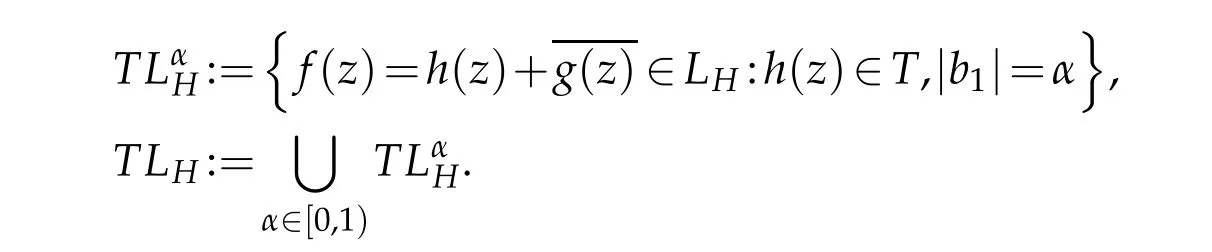
Definition 2.2.Forα∈[0,1),let

Forf∈TLαH,applying Theorem 1.1 and Lemma 1.1,we can prove the following theorem.

Theorem 2.1.If f∈TLαH,then|an|≤1/n,n=2,3,...,and

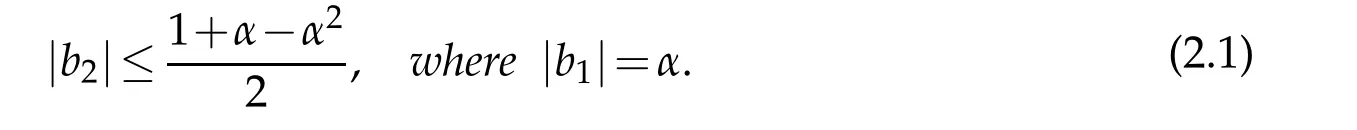
It is sharp estimate for|b2|,the extremal functions are

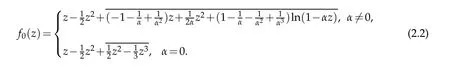
Moreover,

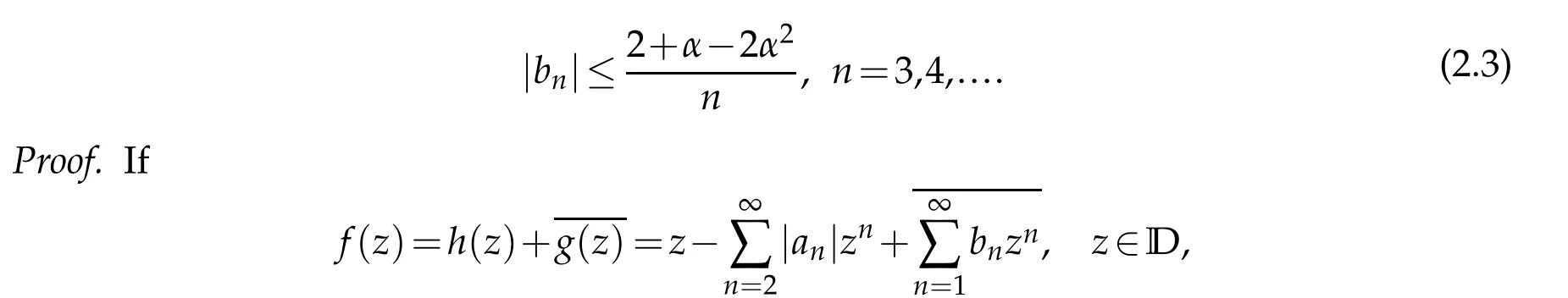
then|an|≤ 1/nby Theorem 1.1.Letg′(z)=ω(z)h′(z),whereω(z)is the dilatation off.

Sinceω(z)is analytic in D,it has a power series expansion

wherecn∈C,n=0,1,2,...,and|c0|=|ω(0)|=|g′(0)|=|b1|=α.Recall that|ω(z)|＜1 for allz∈D,then by Lemma 1.1,we have

Together with the formula(1.3),(1.5)and(2.4),we give

Hence,we obtain

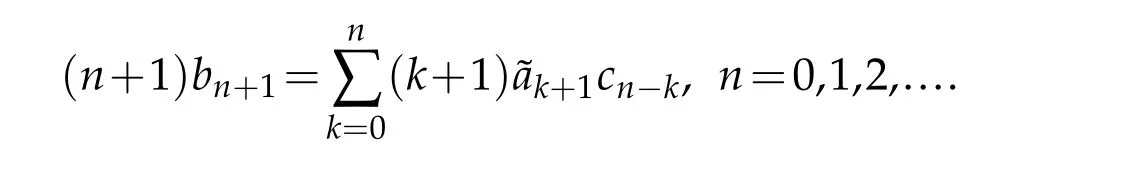
Applying the facts(1.6)and(2.5),and by simple calculation,we have

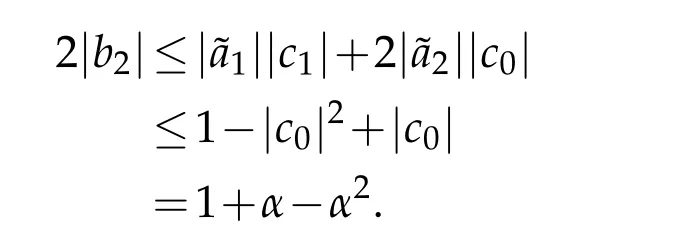
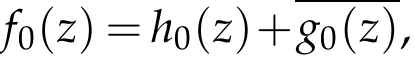
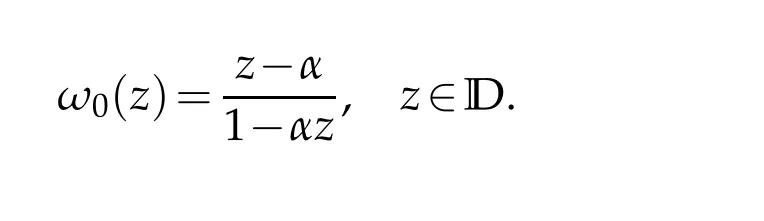
Applying the formula(1.5),we obtain

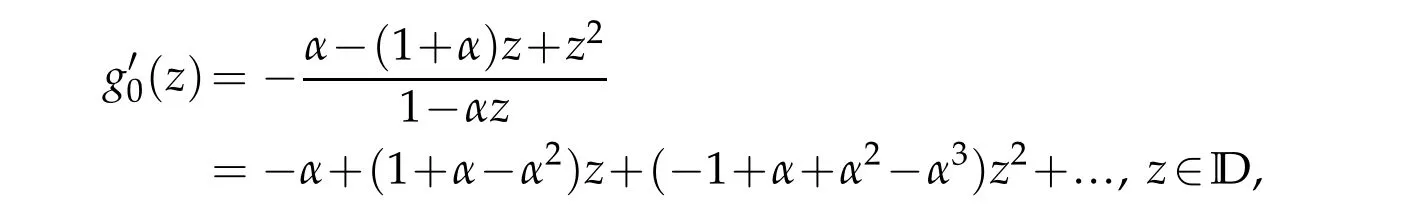
which implies the estimate of(2.1)is sharp.Sinceg0(0)=0,by integration,we uniquely deduce

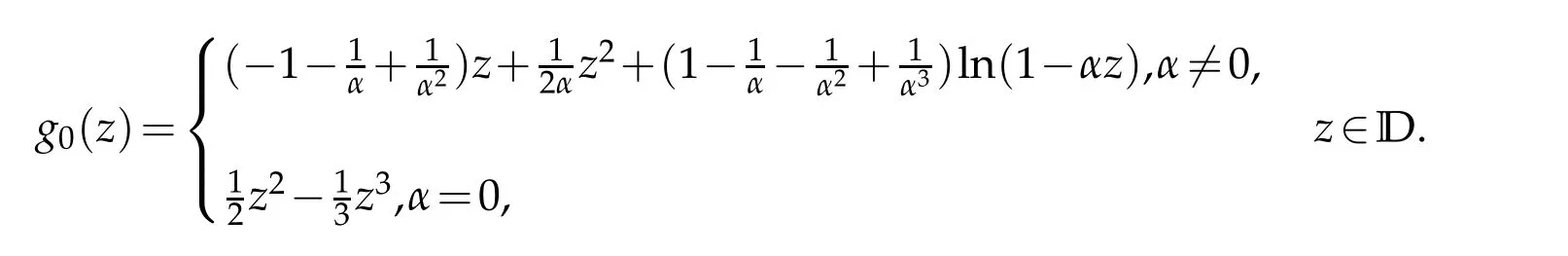
Obviously,|ω0(z)|＜1,z∈D,which meansf0(z)=h0(z)+g0(z)∈TLαH.

In the same way,

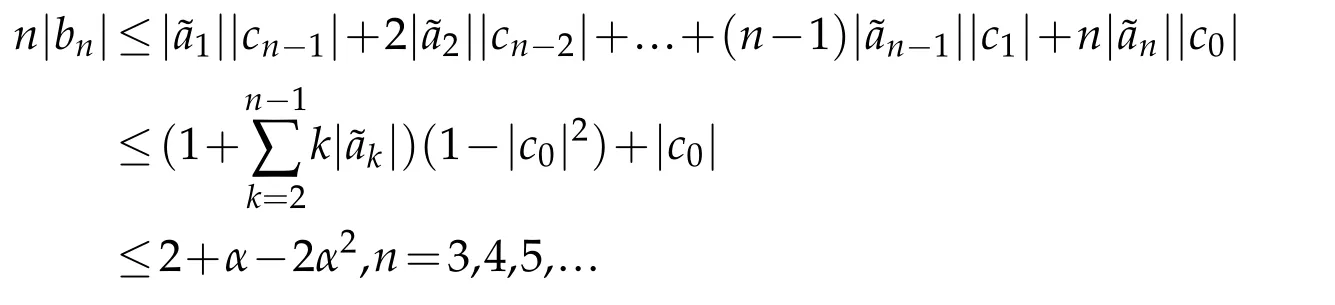
Hence,the proof is completed.

Corollary 2.1.If

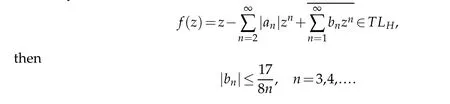
Proof.By simple calculation,we have

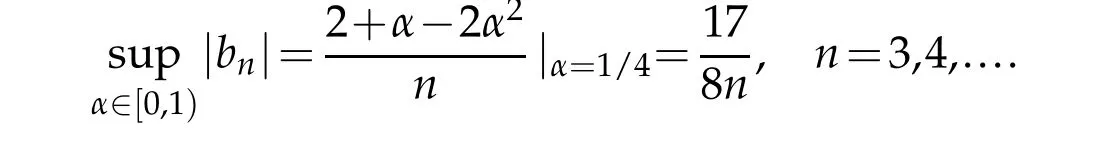
then the corollary follows immediately from Theorem 2.1.

Since the analytic parthoff∈TLαHbelongs toT,we have the following distortion estimate ofhby Theorem 1.2[9]

Our next aim is to give the distortion estimate of the co-analytic partgoff∈TLαH.

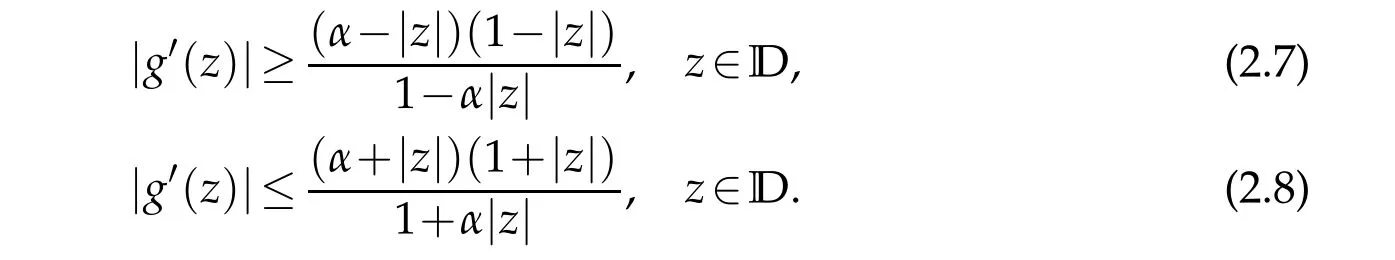
These inequalities are sharp.The equalities hold for the harmonic function f0(z)which is defined in(2.2).

Proof.Letb1=g′(0)=αeiψ.Consider the function

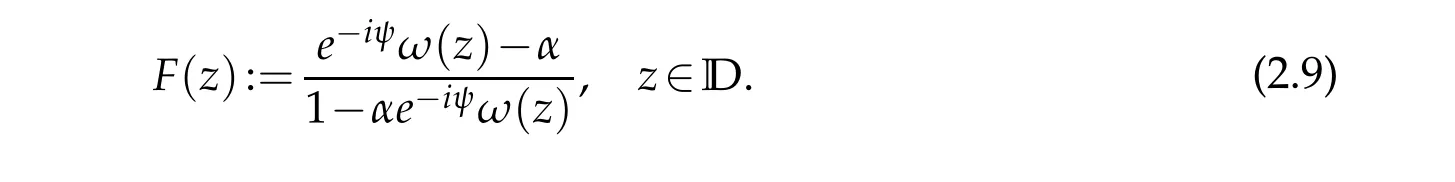
It satisfies assumptions of the Schwarz lemma,which gives

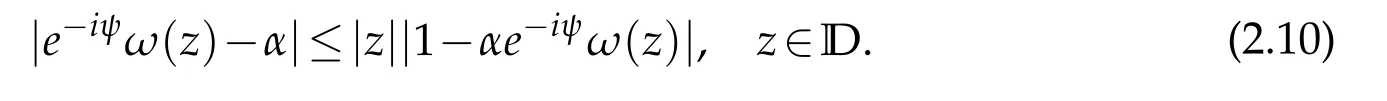
It is equivalent to

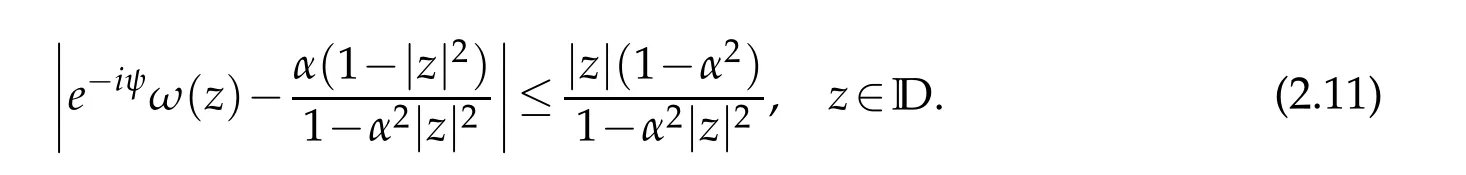
and the equality holds only for the functions satisfying

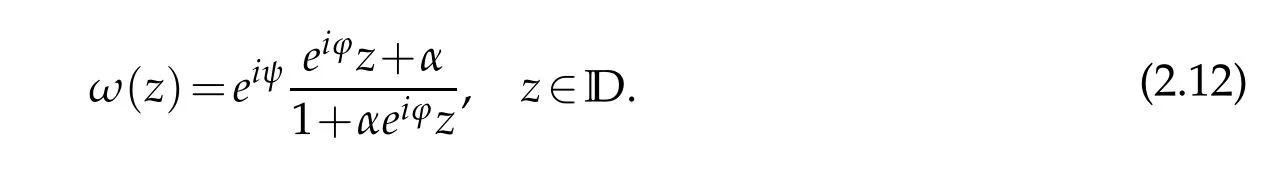
where?∈R.Hence,applying the triangle inequalities and the formula(2.11)we have

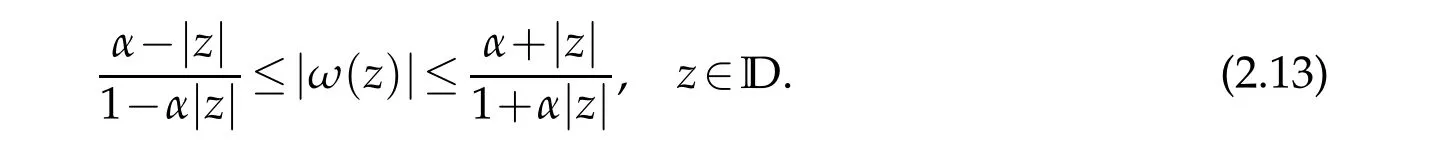
Finally,applying the formula(2.6)together with(2.13)to the identityg′=ωh′,we obtain(2.7)and(2.8).The functionf0(z)defined in(2.2)shows that inequalities(2.7)and(2.8)are sharp.The proof is completed.

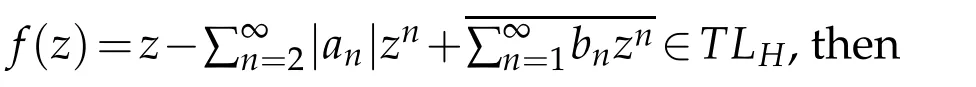
Proof.Letαtend to 1 in the estimate(2.8),then the corollary follows from theorem 2.2 immediately.

From the Theorem 1.3[9],we can get the growth estimate of the analytic parthoff∈TLαH

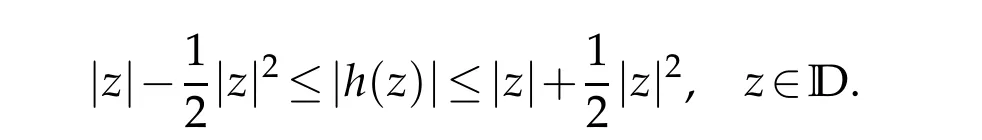
Next results,we give the growth estimate of co-analytic partgoff∈TLαH.

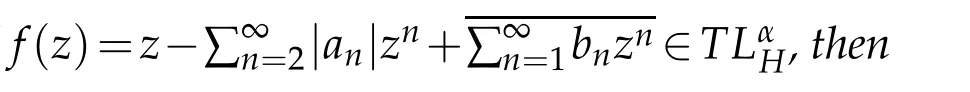
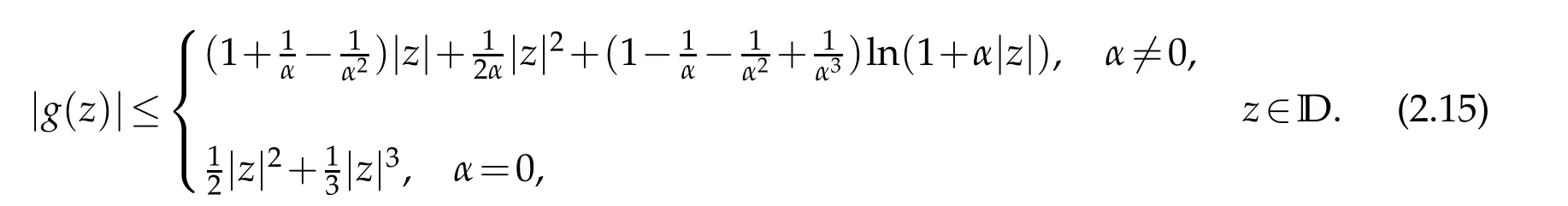
The inequality is sharp.The equality hold for the harmonic function f0(z)which is defined in(2.2).

Proof.Let Γ:=[0,z],applying the estimate(2.8)we have

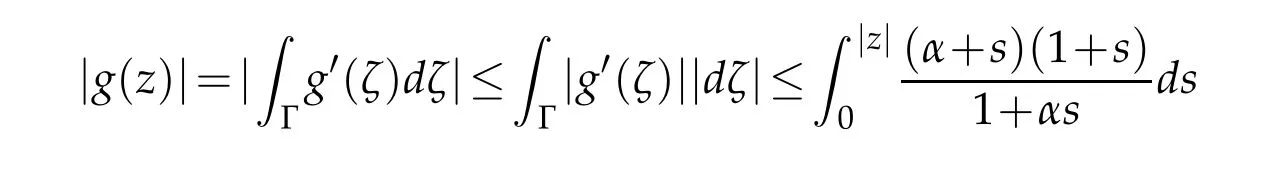
By integration,we obtain the estimate(2.15).The functionf0(z)defined(2.2)shows that the inequality(2.15)is sharp.

Using the distortion estimates in Theorem 1.2[9]and Theorem 2.2,we can easily deduce the following Jacobian estimates off∈TLαH.

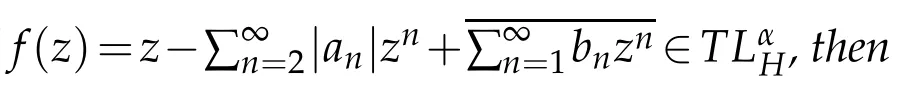
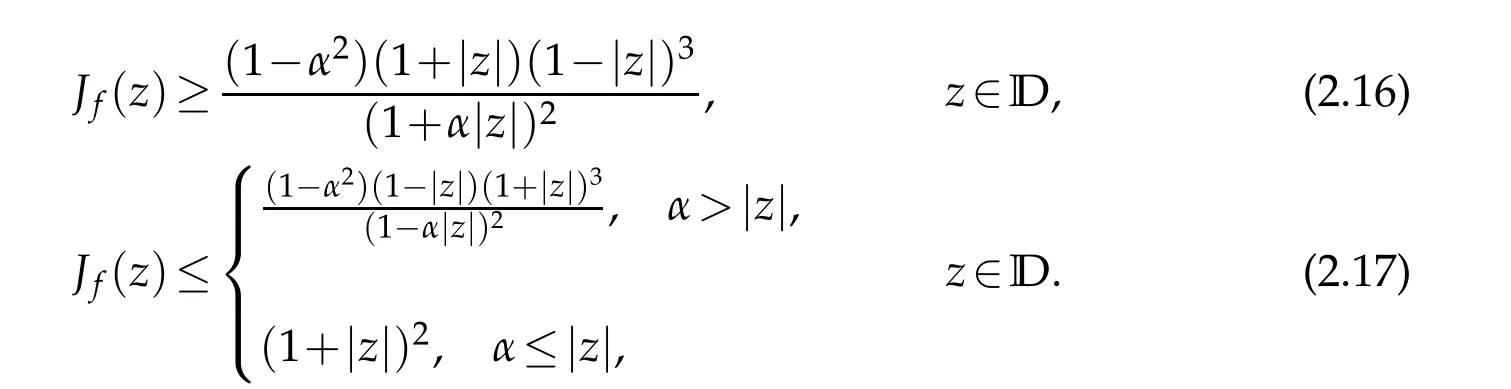
Proof.Observe that iff∈TLαH,thenh′does not vanish inD.We can give the Jacobian offin the form

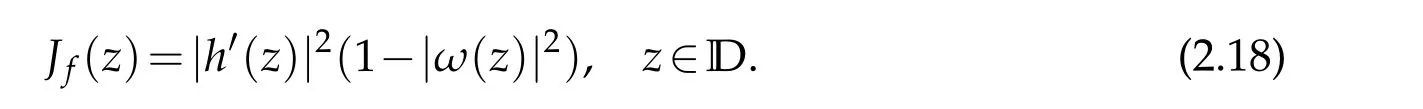
whereωis the dilatation off.Applying(2.6)and(2.13)to the(2.17)we obtain

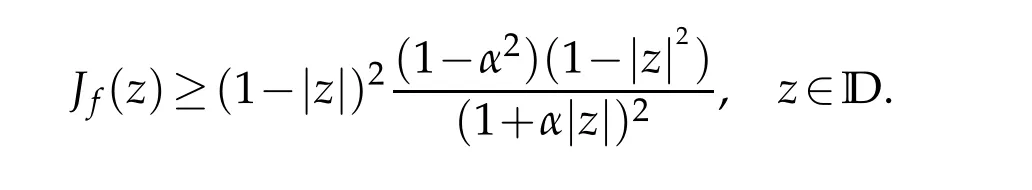
and

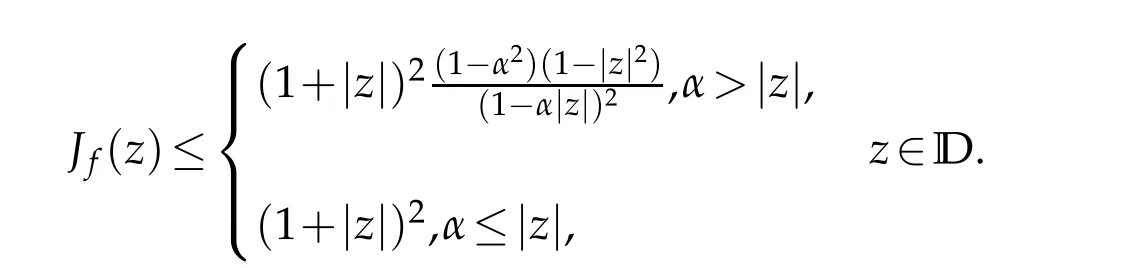
this completes the proof.

Since every univalent function is locally univalent,we can give the growth estimate off∈TSαH.

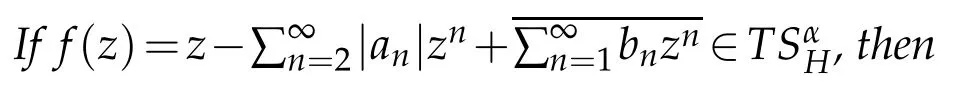
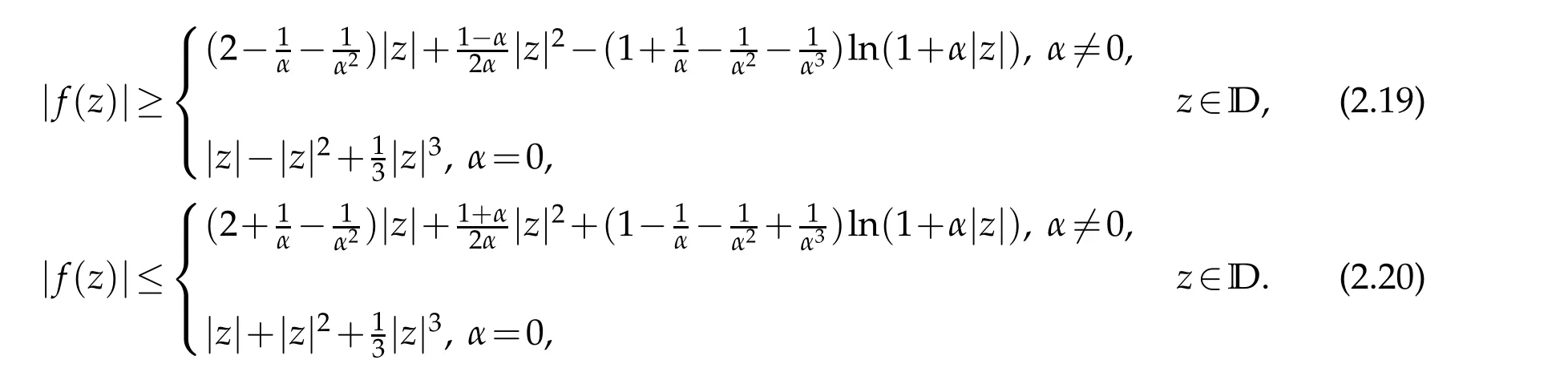
Proof.For any pointz∈Dand supposer:=|z|,we denoteDr:=D(0,r)={z∈D:|z|＜r},and let

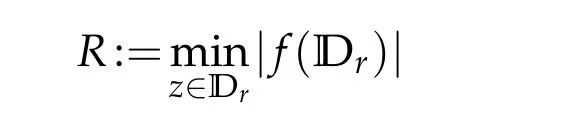
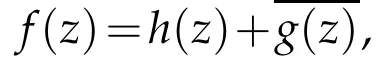
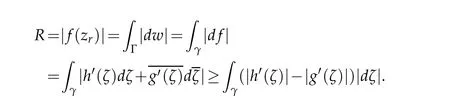
Byg′=ωh′and the formula(2.6)and(2.13),we obtain

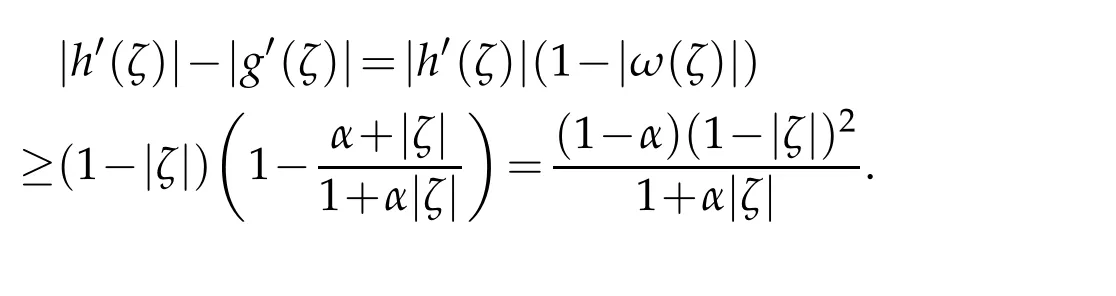
Hence,we have

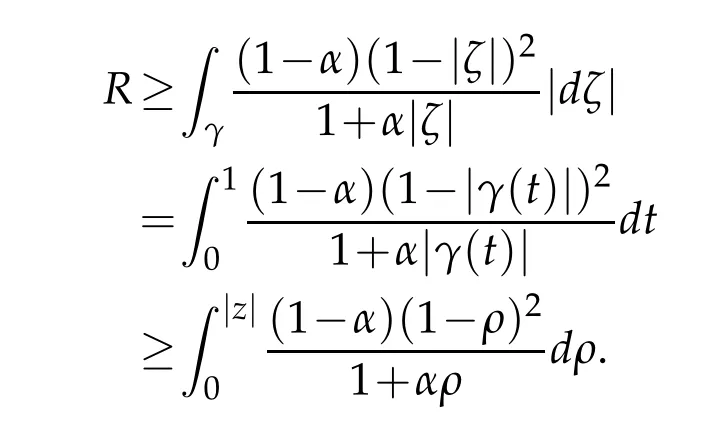
Integrating,we obtain the estimate(2.19).To prove(2.20)we simply use the inequality

Then,by the formula(1.8)and(2.15)with simple calculation we have(2.20),this completes the proof.

Finally,the growth estimate off∈TSαHyields a covering estimate.

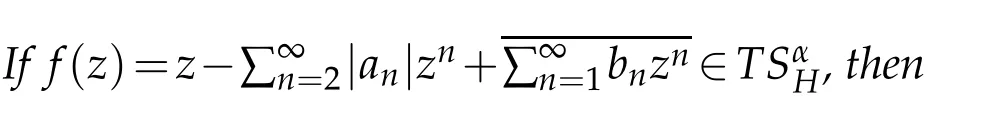
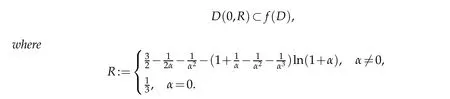
The images of α∈[0,1)■→R are shown in Figure 1.

Proof.If we let|z|tend to 1 in the estimate(2.19),then the Theorem 2.6 follows immediately from the argument principle for harmonic mappings.

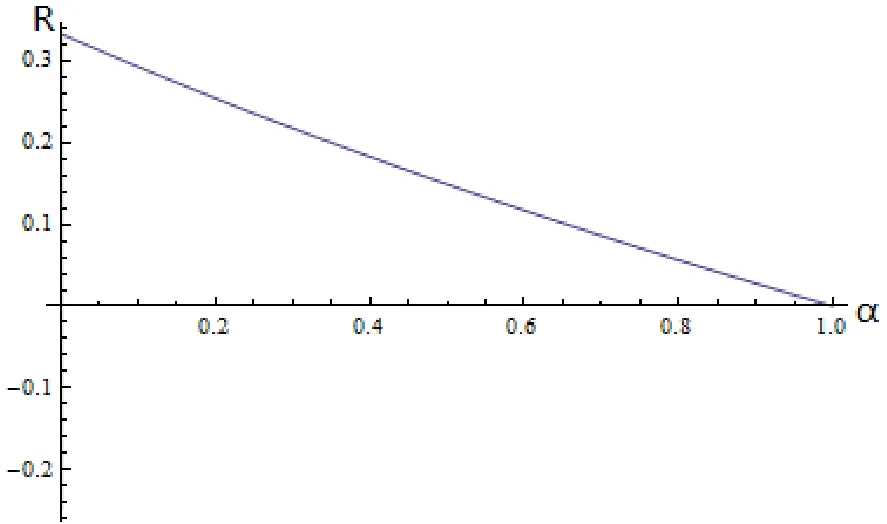
Figure 1:The image of

Acknowledgments

The authors are grateful to the referees for their useful comments and suggestion.This work is partially supported by NNSF of China(11101165),the Natural Science Foundation of Fujian Province of China(2014J01013),NCETFJ Fund(2012FJ-NCET-ZR05),Promotion Program for Young and Middle-aged Teacherin Science and Technology Research of Huaqiao University(ZQN-YX110).

[1]P.Duren.Harmonic mappings in the plane.Cambridge Univ.Press,Cambridge,2004.

[2]I.Hotta and A.Michalski.Locally one-to-one harmonic functions with starlike analytic part.Preprint,available from http://arxiv.org/abs/1404.1826.

[3]J.G.Clunie and T.Sheil-Small.Harmonic univalent functions.Ann.Acad.Sci.Fenn.Ser.A.I.Math.9:3-25,1984.

[4]H.Lewy.On the non-vanishing of the Jacobian in certain one-to-one mappings.Bull.Amer.Math.Soc.,42:689-692,1936.

[5]H.Silverman.Univalent functions with negative coefficients.Proc.Amer.Math.Soc.,51(1):109-116,1975.

[6]G.Karpuzov,Y.Sibel,M.¨Ozt¨urk,and M.Yamankaradeniz.Subclass of harmonic univalent functions with negative coefficients.Appl.Math.Comput.,142(2-3):469-476,2003.

[7]D.Klimek,A.Michalski.Univalent anti-analytic perturbation of the identity in the unit disc.Sci.Bull.Chelm.,1:67-78,2006.

[8]D.Klimek and A.Michalski.Univalent anti-analytic perturbation of convex conformal mapping in the unit disc.Ann.Univ.Mariae Curie-Sklodowska Sect.A,61:39-49,2007.

[9]Qin Deng.On univalent functions with negative coefficients.Appl.Math.and Comput.,189:1675-1682,2007.

[10]I.Graham and G.Kohr.Geometric Function Theory in One and Higher Dimensions.Marcel Dekker Inc,New York,2003.

[11]X.Z.Huang.Estimates on Bloch constants for planar harmonic mappings.J.Math.Anal.Appl,337(2):880-887,2008.

[12]S.Kanas and D.Klimek.Harmonic mappings pelated to functions with bounded boundary rotation and norm of the pre-schwarzian derivative.Bull.Korean Math.Soc.51(3):803-812,2014.

[13]P.Duren.Univalent functions.Springer-Verlag,Berlin-New York,1975.

22 May,2015;Accepted 9 July,2015

?Corresponding author.Email addresses:ZMK900116@163.com(M.Zhu),huangXZ@hqu.edu.cn(X.Huang)