Fault detection and optimization for networked control systems with uncertain time-varying delay

Qing Wang,Zhaolei Wang,2,*,Chaoyang Dong,and Erzhuo Niu

1.School of Automation Science and Electrical Engineering,Beihang University,Beijing 100191,China;

2.Beijing Aerospace Automatic Control Institute,Beijing 100854,China;

3.School of Aeronautic Science and Engineering,Beihang University,Beijing 100191,China;

4.Flight Automatic Control Research Institute,Aviation Industry Corporation,Xi’an 710065,China

Fault detection and optimization for networked control systems with uncertain time-varying delay

Qing Wang1,Zhaolei Wang1,2,*,Chaoyang Dong3,and Erzhuo Niu4

1.School of Automation Science and Electrical Engineering,Beihang University,Beijing 100191,China;

2.Beijing Aerospace Automatic Control Institute,Beijing 100854,China;

3.School of Aeronautic Science and Engineering,Beihang University,Beijing 100191,China;

4.Flight Automatic Control Research Institute,Aviation Industry Corporation,Xi’an 710065,China

The observer-based robust fault detectionlter design and optimization for networked control systems(NCSs)with uncertain time-varying delays are addressed.The NCSs with uncertain time-varying delays are modeled as parameter-uncertain systems by the matrix theory.Based on the model,an observer-based residual generator is constructed and the sufcient condition for the existence of the desired fault detectionlter is derived in terms of the linear matrix inequality.Furthermore,a time domain optimization approach is proposed to improve the performance of the fault detection system.To prevent the false alarms,a new threshold function is established,and the solution of the optimization problem is given by using the singular value decomposition(SVD) of the matrix.A numerical example is provided to illustrate the effectiveness of the proposed approach.

fault detection,networked control systems,residual generator,time-varying delay,time domain optimization approach.

1.Introduction

Networked control systems(NCSs)are feedback control systems in which sensors,controllers,actuators and other system components are connected via a shared communication network[1,2].The new structure has many advantages over the conventional point-to-point system connection,suchas low cost,simpleinstallation andmaintenance, high reliability,and enhanced resource utilization,which makes the NCS a promising structure for control systems [3].However,some problems and shortcomings of NCSs, such as bandwidth constraints[4,5],network induced delay[6,7]and packet dropout[8,9],will inevitably increase the complexity of system design and degrade the system performance or even cause instability[10].As an important essential to improve the performance,safety and reliability of dynamic systems,fault detection(FD)for NCSs has recently attracted considerable research attention[11,12].

The network induced delay is one of the activeelds for NCSs researches,and there are three main categories in the FDelds for NCSs with various network induced delays:procurable delay[13,14],known delay’s probability distributions[15,16]and unknown delay[17–20].So far,there have been already fruitful promising results on the FD for NCSs with procurable delay or known probability distributions delay,but only a limited number of results about FD for NCSs with unknowndelay can be found owing to the high difculties in the treatment.In fact,for most network protocols,time delays are unknown timevarying,and it would be more reasonable to assume that the time delays in NCSs are uncertain.

To deal with the unknown delay,in[17],Taylor expansion was used to approximate the inuence of unknown delay,and then a parity space based FD method was introduced to generate the residual.In[18],based on eigendecomposition,a known structure matrix wasrst extracted from the additional unknown disturbance vector caused by the random and unknown delay,and a parity space approach was used to generate the residual,but the structure matrix was time varying which leads to the increase of design and computation complexity.To overcome this problem,in some work[19,20],the unknown delay’s inuence was transformed into uncertainties of the system, and then the robust FD method based on the reference model was adopted to detect faults.For example,in[19], the unknown delays’inuence was transformed into timevarying polytopic uncertainty based on Cayley-Hamilton theorem,and in[20],it was transformed into parameteruncertainty based on the matrix theory.

In addition,much attention has also been paid to improvethe FD performanceto detectthe faults morequickly and accurately,and the basic idea is to make the generated residual sensitive to the small faults and robust against augmented disturbances,which is called the optimal residual generation problem.To improve the performance of FD systems,the multi-objective H?/H∞trade-offdesignapproachhas beenwidely utilized[21,22], where H?index stands for the residual’s sensitivity,while H∞index can be used to describe the robustness.Meanwhile,based on the parity space approach,a time domain optimization approach is proposed for the traditional FD systems[23,24],where a post-lter is used to enhance the performance of FD systems.While these works are very promising,to the best of the authors’knowledge, the observer-based robust FDlter(FDF)design and optimization problem for the NCSs with parameter uncertainties caused by uncertain time-varying delay has not been investigated yet,which constitutes the main motivation of this paper.

This paper addresses the observer-based robust FDF design and optimization problem for NCSs with unknown time-varying delays.Firstly,based on the matrix theory[25],the unknown time-varying delays in the NCSs are modelled as parameter uncertainties of the system.Secondly,referring to the parameter-uncertain system approach,an observer-basedresidual generatoris constructed,and the robust FD problem is formulated as altering problem to make the error between the residual signal and fault as small as possible.Then,a sufcient condition for the existence of the desired FDF is established in terms of the linear matrix inequality(LMI).Furthermore, a time domain optimization approach is proposed to improve the FD system performance,where the optimal solution of the post-lter can be determined by the matrix singular value decomposition(SVD),and a new threshold is also constructed to prevent false alarms.Finally,a numerical example is provided to illustrate the effectiveness of the proposed approach.

2.Modeling of the NCS

For the NCS shown in Fig.1,the plant is modeled as the following continuous-time linear time-invariant system:

where x∈Rn,u∈Rm,y∈Rl,f∈Rqdenote the state vector,the control input vector,the output vector and the latent fault vector,respectively,d∈Rpis the external disturbance belonging to l2[0,∞).The real matrices Ac,Bc,Bcf,Bcd,C,Ddare of appropriate dimensions.

Fig.1 Structure of NCS

Without loss of generality,the followingassumptions as in[6]are introduced for the studied NCS:

Assumption 1The sensors are clock-driven and the sampling period of the NCS is T,the controller and actuators are event-driven.Data are transmitted in a signal packet during every sampling period,and there are no packet dropout and non-orderedsequence.

Assumption 2The discrete control law is designed as u(k)=?Kx(k).The sensor-controller delay is denoted asand the controller-actuator delay is denotedcan be lumped together aswhich is introducedto describethe uncertaintime-varyingnetwork induceddelay at the time instant k andτmaxis denedas the upperbound of the time-varying delay τk.

Under Assumptions 1 and 2,considering the effect of the delay τkand the sampling period T,system(1)can be transformed into the following discrete time model[19]

From(2),it is easy to see that the discrete NCS model is a time-varying system with uncertain time-varying parameter τkand the parameter τkinuences the system in a multiplicative way,which is very difcult to deal with[26].To overcome this difculty,referring to the networkedcontrolsystemsmodelingapproachin[25],thefollowing Lemma 1 will berstly introducedto transformthe discrete NCS into the parameter-uncertain system.

where B0,B1,D and E are known constant matrices of appropriate dimensions which will be given in the following part,and F(τk)is an unknown matrix with Lebesguemeasurable elements and satises FT(τk)F(τk)≤I.

ProofReferring to the analysis in[25],based on the matrix theory,if the matrix Achas n nonzero distinct eigenvalues λr(r=1,2,...,n),then we have Ac= Λdiag{λ1,...,λn}Λ?1,where Λ=[Λ1,...,Λn],and Λris the eigenvector corresponding to λr.Thus we can rewrite B0(τk)and B1(τk)as follows:

Similarly,it can be easily proved that

where

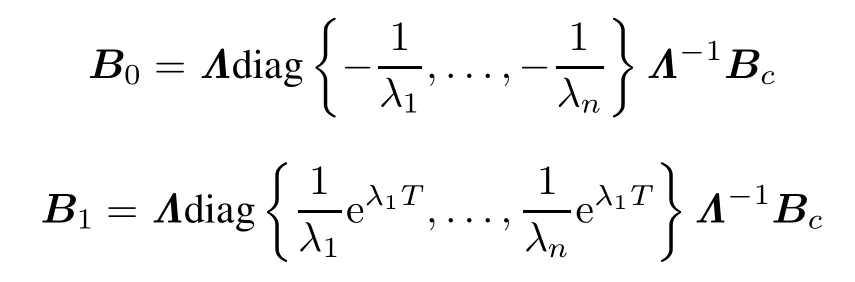
andαiis chosensuchthateλi(T?τk?αi)＜1,i=1,...,n, τk＜T.

Otherwise,if the matrix Achas zero eigenvalues and multiple eigenvalues,without loss of generality,it can be assumed that matrix Achas one eigenvalue 0,eigenvalueλ?with multiplicity r and othersare nonzerodistinct eigenvalues,and the other situations can be easy to deal with in the similar method.Then there exists a nonsingular matrix Λ such that Ac= Λdiag{0,J1,J2}Λ?1,where J1=diag{λ2,...,λn?r}and J2∈ Rr×ris the Jordan block corresponding to λ?.Thus,we can also rewrite B0(τk)and B1(τk)as follows:

Similarly,one has

and α1＞ τk,αiis chosen such that eλi(T?τk?αi)＜ 1, i=2,...,n?r,τk＜T,G2∈Rr×ris a diagonal and invertible matrix and is chosen such that

By Lemma 1,the system(2)can be equivalently written as the following parameter-uncertainsystem:

where B0,B1,D and E are dened in(4)–(7),and F(τk)satises FT(τk)F(τk)≤I.

Applying the state feedback control law u(k) = ?Kx(k)and augmented state z(k) = [xT(k) xT(k?1)]Tto the system(8)results in the following closed-loop parameter-uncertain system model:

3.Problem formulation

For the purpose of FD for the NCS,based on the obtained NCS model in(9),an observer-based FDF is concretelyadopted to generate the residual signal

Set the estimation error e(k)=z(k)??z(k),and then the FD system is governed by

After the above manipulations,the original robust FDF problem for the system(1)can be further convertedtondlter gain matrix L such that the parameter-uncertain system(12)is asymptotically stable and the H∞performance index γ is made as small as possible in the feasibility of

Meanwhile,for improving the performance of the fault detection system(10),a time domain optimization approach is adopted in this paper.Let ξ(k)=V(z)r(k)= (Vs+Vs?1z?1+···+V0z?s)r(k)denote the modied residual signal[27],where the matrix V(z)is called the post-lter[23,27]and the index s is the order of V(z).

According to the system(14)and the denition of ξ(k), we can rewrite ξ(k)in the following compact form:

where

Remark 1It should be noted that the selection of the index s which is the order of the post-lter V(z)is arbitrary in principle.Considering the computational complexity of online implementation,we set it equal to 2n.

For convenience of analysis,we rewrite(15)as

where

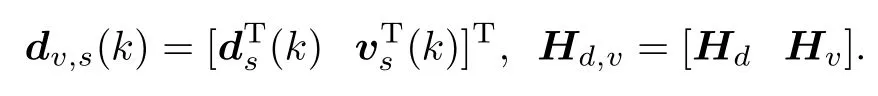
In order to detect the fault,the residual evaluation function and the threshold can be selected as

where α denotes the detection window.

Obviously,the goal of this paper can be generalized tond out thelter gain matrix L and the optimal post-lter matrix V to acquire a desired FD performance,and after that,the faults can be observed by comparing J(k)with the threshold Jthaccording to the following logic:

4.Main results

4.1Filter gain design

Lemma 2[28] Consider the following discrete LTI system ?

Given γ＞0,if there exists the matrix P＞0,LMI

holds,thenthe system is asymptoticallystable andsatises (13).

Lemma 3[29–30]For any matrices M,N and F(k) with FT(k)F(k)≤I,and any scalar ε＞0,the following inequality holds

As an application of Lemma 2 and Lemma 3,the following theorem provides sufcient conditions for the existence of an admissible H∞FDF with the form of(10).

Theorem 1Consider the system(12)and let γ＞0 be a given scalar.If there exist matrices P1＞0,P2＞0,G and scalar ε＞0,such that the following LMI

holds,then system(12)is asymptotically stable with an H∞performance γ.Moreover,thelter gain of an admissible H∞FDF with the form of(10)is given by L=Meanwhile,the following matrix are given:

ProofFromLemma2 andtheparameter-uncertainsystem(12),we can obtain

By the Schur complement,(23)is equivalent to

Without losing generality,we can readily obtain the following inequality by replacingˉA,ˉB,ˉC,ˉD into(24)

where

where

According to Lemma 3,(26)holds if and only if the following inequality is satised for any ε

Remark 2The optimal H∞performance γ?and the corresponding FDF gain matrix can be obtained by setting δ=γ2and solving the following optimization problem:

4.2Determination of threshold

From(16)and(17),we can determine the threshold as

It should be pointed out that the above threshold is the minimum threshold that prevents false alarms.It follows from(15)and(16)that

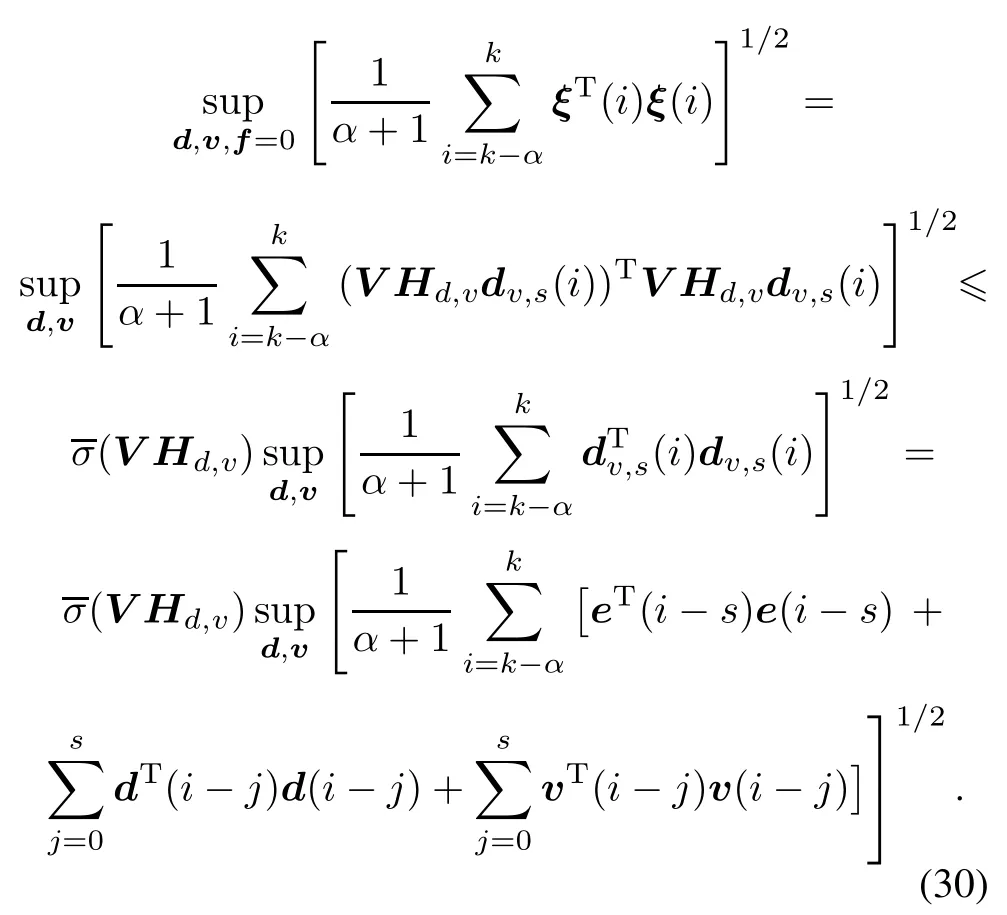
From(14),we can obtain

where

So we have

From(9),it is easy to show that

where

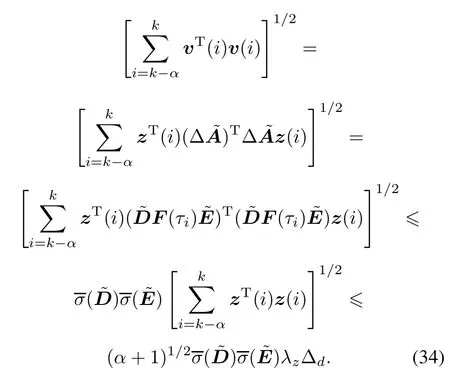
Then we can have

As

then we have

Therefore,the threshold Jthcan be dened as

4.3Post-flter gain design

For improvingthe FD capability of the system(12),an optimal post-lter V in(15)is required to be obtained using the time domain optimization technic in order to detect the faults as small as possible.Firstly,we give the following denitions[23]which can be used as the performance index to describe the FD capability.

Defnition 1The set of detectable faults which are denoted by Sfcan be expressed by

Defnition 3Maximal minimum detectable faults,denoted by fmmin,are dened by

Note that the smaller fmminbecomes,the smaller faults can be detected.Thus,our objective of optimizing can be formulated as the following performance index

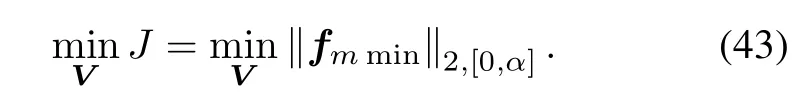
According to(40),we know the detectable faults can satisfy the following form:

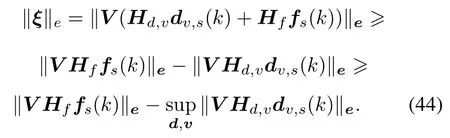
Then we have

and furthermore

Thus,we can obtain(47)from(40),(45)and(46)

where

Since

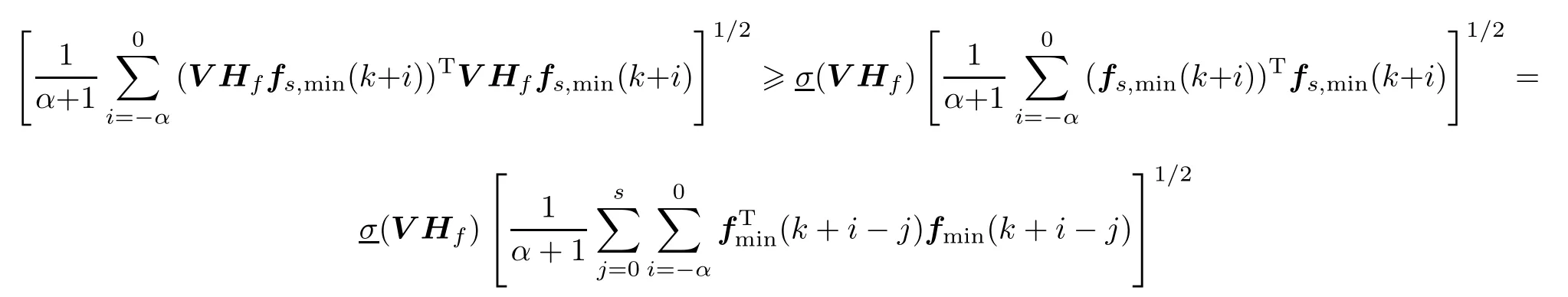
where σ(·)denotes the minimum singular value,Thus,

and are equal to the eigenvector of matrix(V Hf)TV Hfcorrespondingto the eigenvalue,then the equality in(49)holds true.According to the denition of faults fmmin,wenally have

Thus,we can know from(42),(43)and(51)that the objective of optimizing system(12)is reduced tond matrix V that satises the following optimization problems:

From(39),we know the optimization problems in(52) can be furthermore rewritten as follows:

From Theorem 1 and(9),(33),(36),we know that λd, λz,σ(?D)and σ(?E)are constants which can be calculated off-line.Thus the original optimization problem(53) is equivalent to the following optimization problem:

The solution of(54)is not unique,and there exist some theoremsto derivetheoptimizationsolution.Next,we give the following lemma that plays a key role in deriving the optimization solution of(54).

Lemma 4The SVD of a matrix Ω ∈Rλ×δcan be expressed by

where U ∈ Rλ×λ,Θ ∈ Rδ×δ,and UUT= Iλ×λ,ΘΘT=Iδ×δ.For λ＞δ

and for λ≤δ

with σ1≥···≥σλdenoting the singular values of Ω.

Based on Lemma 4,we have Theorem 2 to determine the optimal solution for(54).

Theorem 2Given matrices Hd,v∈Rλ×δand Hf∈Rλ×βwhich are dened as(15)and(16),where λ= l(s+1),β=q(s+1)and δ=(p+2n)(s+1)+2n,then the optimal solution V∈Rλ×λfor(54)is given by

Furthermore,

ProofIt is easy to see that λ＜δ,using Lemma 4 to do an SVD of Hd,vgives

with UUT= Iλ×λ,ΘΘT= Iδ×δ,Σ = [diag{σ1,...,σλ} 0λ×(δ?λ)].

Then any matrix V can be expressed as

where S=diag{σ1,...,σλ},so from(58)and(59)it turns out that

and substituting it into(54),we have

Note that σ(ˉV S?1UTHf)≤ σ(ˉV)σ(S?1UTHf), we have

and the equality holds true if and only if

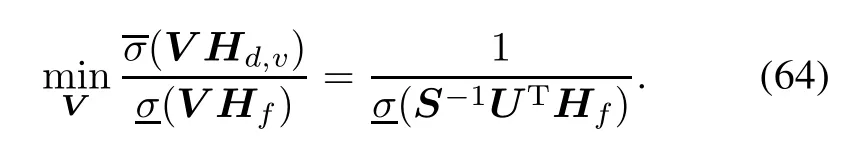
Hence,the optimal solution V for(54)is given by

Remark 3It is worthwhile to point out that the optimal post-lter V actually depends on the observer-basedlter L,which means the gain of V will change with the variety of the H∞performance index γ.It can be easily found from(56)that the optimal V is dependent on the matrix Hd,v

Δ=[HdHv]which is dened in(16).Considering the matrices Hdand Hvare constructed by the matrix AL= ?A?L?C,thelter L is pre-designed using the H∞performance index in(13).Thus,it can be seen that the optimal post-lter V is dependent on the H∞performance index.

However,owing to the fact that thelter L is independentonthe post-lterV(z)andcanbeobtainedseparately, thepost-lterV(z)canbeimmediatelyobtainedfrom(56) once thelter L has been determined.Thus,thelter L and the post-lter V(z)can be truly designed separately in this meaning,although V is depended on L.

Remark 4From(53),it can be seen that the optimal V is designed to detect the faults as small as possible,and this will no doubt reduce the detection delay Tdwhich is dened as the time cost on the detection.Therefore,the post-lter can make the FD system more sensitive to the smaller faults and reduce the detection delay,but cannot eliminate the detection delay completely owing to the fact that the goalJ in(53)cannotbe guaranteedto be 0 for all situations.

4.4Solution procedure

The following Algorithm 1 is given out to summarize the essential parts of this section and the approach proposed above for the FD system design.

Algorithm 1

Step 1Solve the optimal H∞problem in Theorem 1 and Remark 2 for L.

Step 2Generateresidual signa

Step 3Construct Hv,Hd,Hf,and Hd,v.

Step 4Do an SVD on Hd,v,and calculate U,S using (58)and(59).

Step 5Set the optimal post-lter V=S?1UT.

Step 6Establish the threshold

Step 7Let ξ(k)=V(z)r(k)denote the modied residual signal,then the residual evaluation function is

From Algorithm 1,it can be easily known that these steps are implemented off line except Step 2 and Step 7.

5.Numerical example

A numerical example is given to show the effectiveness of the proposed method.Consider the following continuousplant model

Supposethat the sampling periodof NCS is T=0.01 s, the network induced delay τkis less than one sampling period and is a random sequence uniformly distributed between 0 and T,then we can easily obtain parameteruncertain system(8)with the following parameters:

Using the discrete control law u(k) = ?0.613 6 0.760 8?x(k), the optimal H∞performance index is γ? = 0.01 and the gain matrix for the observer-based FDF is L = ?0.443 2 ?0.200 5 0.400 7 ?0.190 8?Tby solving the optimization problem(28).In what follows,according to Theorem 2,we can obtain the optimal solution from optimization problem(54)as follows:

Theinitial state is set to be x(0)=[0 0]T.The external disturbance d(t)is supposed to be a random sequence uniformly distributed over[?0.5,0.5],and the slow variation fault signal f(t)which is shown in Fig.2 is given as

where fais the maximal value of f(t).

Fig.2 Slow variation fault signal

Setting the detection window α=10 and the upper bound of time delay τmax=T,simulation results with and without optimization are given in Fig.3 and Fig.4 for the faults with fa=1 and fa=0.5 respectively.

Fig.3 Simulation result when fa=1,τmax=T

Fig.4 Simulation result when fa=0.5,τmax=T

Form Fig.3 it can be seen that the residual signal r(k) reects the fault f(t)when it occurs,and obviously,the FD system with optimization is more sensitive to the faults and needs fewer time steps to detect the fault,that is to say that the FD system with optimization can detect smaller faults quickly than the FD system without optimization.

Furthermore,to show the effectiveness of our approach, we give another simulation and compare the proposed approach to existing results in[19],and the residual signals and corresponding thresholds are also constructed in the same conditions accordingto[19].The simulation result is given in Fig.5 for τmax=T and fa=0.5.

By comparing Fig.4 and Fig.5,it can be seen that the performance of the approach in[19]is better than the FD system without optimization,but the optimization technic can further enhance the performance of the FD system to detect the faults more quickly and accurately.

Fig.5 Simulation result with approach in[19]when fa=0.5, τmax=T

Furthermore,in order to analyze the inuence of the time delay on the FD system,other simulations are also performed when τmax=0.1T.Meanwhile,the maximal value faof the fault is decreased step by step with a step Δf=0.025 to validate the FD speed and the small FD capability.The minimum detectable faand the related detection delay Tdcan be obtained by 100 times simulations separately for τmax=T and τmax=0.1T,and the results are given in Table 1.

Table 1 fa,and Tdfor different situations

It canbefoundfromTable 1that ourmethodhas a better performance,and the time-varying delay will degrade the performance of the FD system,where the robust FD strategy and the time domain optimization technic are necessary to restrain the inuence of the time delay and improve the FD system performance.

6.Conclusions

The problem of observer-based robust FDF design and optimization for NCSs with uncertain time-varying delays is addressed in this paper.The inuence caused by uncertain time-varying delays is transformed into parameteruncertainty with the matrix theory.Under the parameteruncertain system,the LMI-based sufcient condition of FDF is obtained and a time domain optimization approach with the new threshold functionis proposedto improvethe performance of the FD system.An illustrative numerical exampleis presentedtoshowthattheproposedmethodcan detect smaller faults and need fewer times.

[1]L.A.Montestruque,P.J.Antsaklis.On the model-based control of networked systems.Automatica,2003,39(10):1837–1843.

[2]Q.Ai,C.Liu,B.Jiang.Robust fault detection for a class of nonlinear network control system with communication delay. Journal of Systems Engineering and Electronics,2009,20(5): 1024–1030.

[3]W.Zhang,M.S.Branicky,S.M.Philips.Stability of networked control systems.IEEE Trans.on Control Systems, 2001,21(1):84–99.

[4]X.G.Zhang,A.Cela,S.I.Niculescu,et al.Some problems in the stability of networked-control systems with periodicscheduling.International Journal of Control,2010,83(5): 996–1008.

[5]L.Shi,P.Cheng,J.M.Chen.Optimal periodic sensor scheduling with limited resources.IEEE Trans.on Automatic Control, 2011,56(9):2190–2195.

[6]W.A.Zhang,L.Yu,S.Yin.A switched system approach to H∞control of networked control systems with time-varying delays.Journal of the Franklin Institute,2011,348:165–178.

[7]Y.Zhang,H.Fang,Z.Luo.H∞-based fault detection for nonlinear networked systems with random packet dropout and probabilistic interval delay.Journal of Systems Engineering and Electronics,2011,22(5):825–831.

[8]J.Xiong,J.Lam.Stabilization of linear systems over networks with bounded packet loss.Automatica,2007,43(1):80–87.

[9]X.Fang,J.Wang.Stochastic observer-based guaranteed cost control for networked control systems with packet dropouts. IET Control Theory Applications,2008,2(11):980–989.

[10]X.He,Z.D.Wang,D.H.Zhou.Robust fault detection for net-worked systems with communication delay and data missing. Automatica,2009,45(11):2634–2639.

[11]X.He,Z.D.Wang,Y.D.Ji,et al.Network-based fault detection for discrete-time state-delay systems:a new measurement model.International Journal of Adaptive Control and Signal Processing,2008,22(5):510–528.

[12]Z.Zhu,X.Jiao.Fault detection for nonlinear networked control systems based on fuzzy observer.Journal of Systems Engineering and Electronics,2012,23(1):129–136.

[13]Y.Zheng,H.J.Fang,H.Wang,et al.Observer-based FDI design of networked control system with output transfer delay. Control Theory and Applications,2003,20(5):653–656.

[14]Y.Zheng,X.L.Hu,H.J.Fang,et al.Research on observerbased fault diagnosis of networked control system.Systems Engineering and Electronics,2005,27(6):1069–1072.(in Chinese)

[15]Z.H.Mao,B.Jiang,P.Shi.H∞fault detectionlter design for networked control systems modeled by discrete Markovian jump systems.IET Control Theory and Applications,2007, 1(5):1336–1343.

[16]L.X.Zhang,E.K.Boukas,L.Baron,et al.Fault detection for discrete-time Markov jump linear systems with partially known transition probabilities.International Journal of Control,2010,83(8):1564–1572.

[17]H.Ye,S.X.Ding.Fault detection of networked control systems with network-induced delay.Proc.of the 8th International Conference on Control,Automation Robotics and Vision,2004:294–297.

[18]Y.Q.Wang,H.Ye,G.Z.Wang.Fault detection of NCS based on eigendecomposition,adaptive evaluation and adaptive threshold.International Journal of Control,2007,80(12): 1903–1911.

[19]Y.Q.Wang,S.X.Ding,H.Ye,et al.A new fault detectionscheme for networked control systems subject touncertain time-varying delay.IEEE Trans.on Signal Processing,2008, 56(10):5258–5268.

[20]Y.Q.Wang,H.Ye,S.X.Ding.Fault detection of networked control systems based on optimal robust fault detectionlter. Acta Automatic Sinica,2008,34(12):1534–1539.

[21]J.L.Wang,G.H.Yang,J.Liu.An LMI approach to H-index and mixedH?/H∞fault detection observer design.Automatica,2007,43(9):1656–1665.

[22]M.Chadli,A.Abdob,S.X.Ding.H?/H∞fault detectionlter design for discrete-time Takagi-Sugeno fuzzy system.Automatica,2013,49(7):1996–2005.

[23]X.Ding,L.Guo.An approach to time domain optimization of observer-based fault detection systems.International Journal of Control,1998,69(3):419–442.

[24]M.Y.Zhong,S.X.Ding,E.L.Ding.Optimal fault detection for linear discrete time-varying systems.Automatica,2010, 46(8):1395–1400.

[25]W.H.Fan,H.Cai,Q.W.Chen,et al.Stability of networked control systems with time delay.Control Theory and Application,2004,21(6):880–884.

[26]Y.Q.Wang,H.Ye,G.Z.Wang.Recent development of fault detection techniques for networked control systems.Control Theory and Application,2009,26(4):400–409.

[27]M.Abid,W.Chen,S.X.Ding,et al.Optimal residual evaluation for nonlinear systems using post-lter and threshold. International Journal of Control,2011,84(3):526–539.

[28]M.Y.Zhong,S.X.Ding,J.Lam,et al.An LMI approach to design robust fault detectionlter for uncertain LTI systems. Automatica,2003,39(3):543–550.

[29]A.D.Liu,Y.Liu,W.A.Zhang.H∞control for network-based systems with time-varying delay and packet disordering.IET Control Theory and Applications,2007,1(5):1344–1354.

[30]C.X.Yang,Z.H.Guan,J.Huang.Stochastic fault tolerant control of networked control systems.Journal of the Franklin Institute,2009,346(10):1006–1020.

Biographies

Qing Wang was born in 1968.She received her M.E.and Ph.D.degrees inight vehicle control guidance and simulation from Northwestern Polytechnical University,in 1993 and 1996,respectively.She worked as a post-doctoral researcher at the Department of Automatic Control,Beihang University,from 1996 to 1998.She worked in China Academy of Space Technology in 1999. During this period she visited Moscow College of Aeronautics as a visitor.She is currently a professor of guidance,navigation and control,in the School of Automation Science and Electrical Engineering,Beihang University.Her research interests are guidance and control of aerospace vehicles and intelligentight control system.

E-mail:wangqing@buaa.edu.cn

Zhaolei Wang was born in 1986.He received his B.S.degree in automation from Beijing Institute of Technology in 2009.He is now a Ph.D.candidate of navigation,guidance and control,in the School of Automation Science and Electrical Engineering, Beihang University.He is now an engineer of Beijing Aerospace Automatic Control Institute,Beijing. His research interests include fault diagnosis,networked control system,switched system theory and its application inight vehicles.

E-mail:beiliwzl123@163.com

Chaoyang Dong was born in 1966.He received his M.E.degree at Northwestern Polytechnical University,in 1992,and Ph.D.degree in guidance,navigation and control from Beihang University.From 2002 to 2008,he was an associate professor in the Department of Automatic Control,Beihang University.He is currently a professor ofight mechanics in the School of Aeronautic Science and Engineering,Beihang University.His research interests are kinetic analysis ofexible vehicles and control of the complex dynamics system.

E-mail:dongchaoyang@buaa.edu.cn

Erzhuo Niu was born in 1983.He received his Ph.D.degree in navigation,guidance and control from Beihang University.He is currently an engineer of the Flight Automatic Control Research Institute of Aviation Industry Corporation,Xi’an.His research interests are control law design,fault detection and networked control systems.

E-mail:nz830111@163.com

10.1109/JSEE.2015.00062

Manuscript received March 04,2014.

*Corresponding author.

This work was supported by the National Natural Science Foundation of China(61074027;61273083).