由Siegel公式導(dǎo)出一個整數(shù)表為8個平方數(shù)之和的表示數(shù)

羅 淼, 譚千蓉

(攀枝花學(xué)院數(shù)學(xué)與計算機(jī)學(xué)院,四川攀枝花617000)

設(shè)m是一個正整數(shù).記

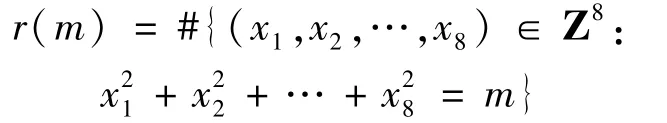
為m能表示成8個平方數(shù)之和的表示方法數(shù),其中#A表示集合A的基數(shù),而Z表示所有整數(shù)的集合.

數(shù)學(xué)家C.G.Jacobi在1828年證明了如下的八平方和公式[1]:

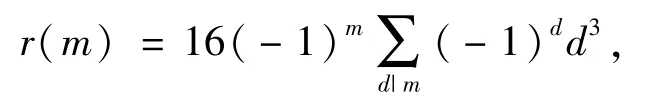
其中,d跑遍m的所有正因子.

在本文中,將用二次型的解析理論中的Siegel公式來給出r(m)的一個表達(dá)式.這個表達(dá)式和Jacobi八平方和公式是等價的.

1 Siegel公式

2 β∞(m)和 βp(m)的計算

3 r(m)的表達(dá)式

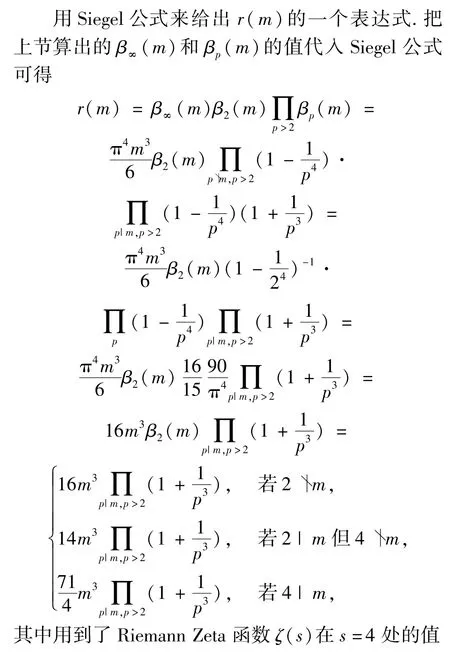
很容易看出這些結(jié)果與用Jacobi八平方和公式算出的結(jié)果是一樣的.

致謝攀枝花學(xué)院培育項目(2012PY08)對本文給予了資助,謹(jǐn)致謝意.

[1]Hardy G H,Wright E M.數(shù)論導(dǎo)引[M].5版.張明堯,張凡,譯.北京:人民郵電出版社,2008:334.

[2]Hanke J.Quadratic forms and automorphic forms[OL].arXiv:1105.5759,2012.

[3]Ireland K,Rosen M.A Classical Introduction to Modern Number Theory[M].2nd ed.New York:Springer-Verlag,1990:103.

[4]Tan Q R,Luo M,Lin Z B.Determinants and divisibility of power GCD and power LCM matrices on finitely many coprime divisor chains[J].Appl Math Comput,2013,219:8112-8120.

[5]Tan Q R.Divisibility among power GCD matrices and among power LCM matrices on finitely many coprime divisor chains[J].Linear Algebra and Its Applications,2013,438:1454-1466.

[6]Tan Q R,Lin Z B,Liu L.Divisibility among power GCD matrices and among power LCM matrices on two coprime divisor chains II[J].Linear and Multilinear Algebra,2011,59:969-983.

[7]Bateman P T.On the representations of a number as the sum of three squares[J].Trans Amer Math Soc,1951,71:70-101.

[8]Cooper S.Sums of five,seven and nine squares[J].Ramanujan J,2002,6:469-490.

[9]Cooper S,Hirschhorn M D.On the number of primitive representations of integers as sums of squares[J].Ramanujan J,2007,13:7-25.

[10]Lin J F.The number of representations of an integeras a sum of eight squares[J].Northeastern Math J,2002,18(1):19-20.

[11]Grosswald E.Representations of Integers as Sums of Squares[M].New York:Springer-Verlag,1985.

[12]Hirschhorn M D.A simple proof of Jacobi's four square theorem[J].Proc Amer Math Soc,1987,101:436-438.

[13]Mordell L J.On the representation of numbers as the sum of 2rsquares[J].Quart J Pure Appl Math,1917,48:93-104.

[14]Olds C D.On the number of representations of the square of an integer as the sum of three squares[J].Amer J Math,1941,63:763-767.

[15]Glaisher J W L.On the numbers of representations of a number as a sum of 2rsquares,where 2rdoes not exceed eighteen[J].Proc London Math Soc,1907,5:479-490.

[16]Ewell J A.On sums of sixteen squares[J].Rocky Mountain J Math,1987,17:295-299.