Cartesian點(diǎn)集Lagrange投影算子的誤差公式
李 喆,孫 艷
(長春理工大學(xué) 理學(xué)院,長春 130022)
Cartesian點(diǎn)集Lagrange投影算子的誤差公式
李 喆,孫 艷
(長春理工大學(xué) 理學(xué)院,長春 130022)
考慮多元插值問題的插值余項(xiàng)估計(jì)問題.針對(duì)好誤差公式的概念,給出了推廣好誤差公式的概念,并以三維Cartesian點(diǎn)集為例,利用B樣條與差商的關(guān)系給出Cartesian點(diǎn)集Lagrange插值誤差公式的積分形式.該結(jié)果可以推廣到d維空間中.
Cartesian點(diǎn)集; Lagrange投影算子; 誤差公式
0 引 言
令F表示特征為零的數(shù)域,F[x]∶=F[x1,…,xd]表示數(shù)域F上的d元多項(xiàng)式環(huán).理想投影算子為定義在F[x]上,核為理想的線性冪零算子[1-3].該理想由所有滿足齊次插值條件的多項(xiàng)式集合構(gòu)成,理想插值包含了Lagrange和Hermite插值.Lagrange插值對(duì)應(yīng)的算子稱為Lagrange投影算子.當(dāng)理想投影算子的核空間為某一有限互異點(diǎn)集Ξ?Fd上的消逝理想時(shí),該理想投影算子為Lagrange投影算子.Lagrange投影算子對(duì)應(yīng)的插值問題是Lagrange插值.Hermite投影算子定義為一列Lagrange投影算子的逐點(diǎn)極限形式[4],其對(duì)應(yīng)的插值問題是Hermite插值.特別地,插值條件僅與方向?qū)?shù)有關(guān)的插值問題屬于Hermite插值.
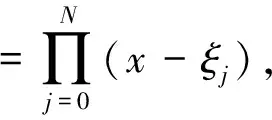
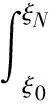
在多元情形中,人們期望理想投影算子也具有與一元情形結(jié)構(gòu)相同的誤差公式.為此,Boor[2]提出了理想投影算子好誤差公式的概念,并證明了張量積節(jié)點(diǎn)和滿足GC條件節(jié)點(diǎn)的Lagrange投影算子具有好誤差公式[10].但Shekhtman[11]證明了一個(gè)非常簡單的二元理想投影算子不具有好誤差公式.所以,Shekhtman相信大多數(shù)理想投影算子不具有好誤差公式.Cartesian點(diǎn)集是一類具有特殊幾何結(jié)構(gòu)的點(diǎn)集,其消逝理想具有唯一的單項(xiàng)商環(huán)基底[12].本文推廣了好誤差公式的概念,利用B樣條與差商的關(guān)系給出三維Cartesian點(diǎn)集的Lagrange投影算子Newton型插值公式及誤差公式的形式,該結(jié)果可推廣到d維Cartesian點(diǎn)集.
1 預(yù)備知識(shí)
設(shè)P為d元多項(xiàng)式環(huán)F[x]上的理想投影算子,則P的像空間和核空間分別為
其中: ranP構(gòu)成F[x]的一個(gè)有限維子空間; KerP構(gòu)成F[x]的一個(gè)理想.
定義1[2]設(shè)P為理想投影算子,{h1,…,hm}為核空間KerP的理想基.若存在齊次多項(xiàng)式Hj和線性算子Cj: F[x]→F[x](j=1,2,…,m),使得對(duì)任何f∈F[x],都有
Hj(D)hk=δj,k, ?j,k=1,2,…,m,
且
則稱理想基{h1,…,hm}支撐好誤差公式.
定義2[13-14]有限互異節(jié)點(diǎn)集合Ξ?Fd稱為Cartesian點(diǎn)集當(dāng)且僅當(dāng)存在lower集A?d和單射函數(shù)yi:→F(i=1,2,…,d),使得Ξ可以表示為

其中對(duì)固定的i及其所有可能的αi,ξi,αi是互不相同的.Ξ也稱為A-Cartesian點(diǎn)集.
2 主要結(jié)果
設(shè)Ξ?F3為A-Cartesian點(diǎn)集,其中

定義mk∶=nk(mk-1,…,m1),其中k=2,3.不失一般性,假設(shè)ξj,0≤…≤ξj,vj,其中0≤v1≤m1,0≤v2≤m2,0≤v3≤m3.定義多項(xiàng)式
定義F[x1,x2,x3]上的線性算子:
式中被積函數(shù)為F[x1,x2,x3]上的多項(xiàng)式,故C1,C2,v1,C3,v1,v2是從F[x1,x2,x3]到F[x1,x2,x3]上的線性算子.對(duì)于函數(shù)f(x1,x2,x3),視x2,x3為固定值,可得關(guān)于變量x1的一元差商:
再視上述差商中的x3為固定,可得關(guān)于變量x1,x2的二元差商:
最后可得關(guān)于變量x1,x2,x3的三元差商:
命題1[13]設(shè)P為三維A-Cartesian點(diǎn)集Ξ上的Lagrange投影算子,其中A由式(2)定義.則

構(gòu)成KerP的理想基.
命題2
證明: 任取0≤i1≤v1,將f(x1,x2,x3)在ξ1,i1處關(guān)于變量x1進(jìn)行Taylor展開,有

由于
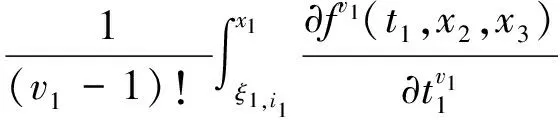
故
因此
而
由式(3)可證式(7)成立.任取0≤i2≤v2,將f(ξ1,i1,x2,x3)在ξ2,i2處關(guān)于變量x2進(jìn)行Taylor展開,有
將式(13)代入式(10)可得
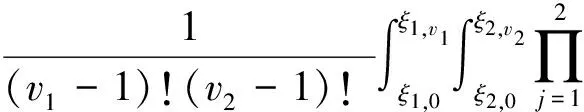
由式(4),(12),可證式(8)成立.任取0≤i3≤v3,將f(ξ1,i1,ξ2,i2,x3)在ξ3,i3處關(guān)于變量x3進(jìn)行Taylor展開,有
將式(15),(13)代入式(10)可得
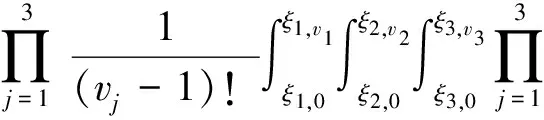
由式(5),(12),可證式(9)成立.證畢.
定理1設(shè)P為三維A-Cartesian點(diǎn)集Ξ上的Lagrange投影算子,則理想基H,齊次多項(xiàng)式H1,H2,v1,H3,v1,v2和線性算子C1,C2,v1,C3,v1,v2滿足條件:
且對(duì)任何f∈F[x1,x2,x3],有

其中: 0≤v1≤m1; 0≤v2≤n2(v1).
證明: 式(17)可直接驗(yàn)證.根據(jù)一元Newton插值公式有
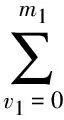
并且
綜上,A-Cartesian點(diǎn)集Ξ上的Lagrange投影算子,其Newton型插值公式為
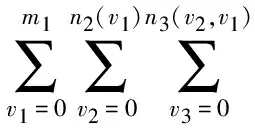
誤差公式為
由命題2可證式(18)成立.證畢.
注1定理1中構(gòu)造誤差公式的方法是形式化的,與維數(shù)無關(guān),所以定理1的結(jié)果可直接推廣到d維空間.
[1]Biekhoff G.The Algebra of Multivariate Interpolation [C]//Constructive Approaches to Mathematical Models.New York: Academic Press,1979: 345-363.
[2]Boor C,de.Ideal Interpolation [C]//Approximation Theory XI,Gatlinburg 2004.Brentwood TN: Nashboro Press,2005: 59-91.
[3]Shekhtman B.Ideal Interpolation: Translations to and from Algebraic Geometry [C]//Approximate Commutative Algebra.New York: Springer-Vienna,2009: 163-192.
[4]Boor C,de,Shekhtman B.On the Pointwise Limits of Bivariate Lagrange Projectors [J].Linear Algebra Appl,2008,429(1): 311-325.
[5]Ciarlet P G,Wagschal C.Multipoint Taylor Formulas and Applications to the Finite Element Method [J].Numer Math,1971,17(1): 84-100.
[6]Ciarlet P G,Raviart P A.General Lagrange and Hermite Interpolation innwith Applications to Finite Element Methods [J].Arch Rational Mech Anal,1972,46(3): 177-199.
[7]Sauer T,XU Yuan.On Multivariate Lagrange Interpolation [J].Math Comp,1995,64: 1147-1170.
[8]Sauer T,XU Yuan.On Multivariate Hermite Interpolation [J].Adv Comput Math,1995,4(1): 207-259.
[9]Boor C,de.On the Error in Multivariate Polynomial Interpolation [J].Appl Numer Math,1992,10(3/4): 297-305.
[10]Boor C,de.The Error in Polynomial Tensor-Product,and Chung-Yao,Interpolation [C]//Surface Fitting and Multiresolution Methods.Nashville TN: Vanderbilt University Press,1997: 35-50.
[11]Shekhtman B.On Non-existence of Certain Error Formulas for Ideal Interpolation [J].J Approx Theory,2010,162(7): 1398-1406.
[12]LI Zhe,ZHANG Shugong,DONG Tian.Finite Sets of Affine Points with Unique Associated Monomial Order Quotient Bases [J].Journal of Algebra and Its Applications,2011,11(2): 1-12.
[13]Sauer T.Lagrange Interpolation on Subgrids of Tensor Product Grids [J].Math Comput,2004,73(245): 181-190.
[14]Chen T,Dong T,Zhang S.The Newton Interpolation Bases on Lower Sets [J].J Inf Comput Sci,2006,3(3): 385-394.
(責(zé)任編輯: 趙立芹)
ErrorFormulasofLagrangeProjectorsforCartesianPointSets
LI Zhe,SUN Yan
(CollegeofScience,ChangchunUniversityofScienceandTechnology,Changchun130022,China)
This paper generalized good error formulas and considered Lagrange interpolation for Cartesian point sets.Taking 3-dimension Cartesian point sets for example,we provided the integral form of error formulas for this class of interpolation problem using the relationship between the B-spline and finite difference quotient.The results can be generalized in thed-dimensional Cartesian point sets.
Cartesian point sets; Lagrange projectors; error formulas
2014-01-24.
李 喆(1981—),女,漢族,博士,講師,從事符號(hào)計(jì)算及符號(hào)數(shù)值混合計(jì)算的研究,E-mail: zheli200809@163.com.通信作者: 孫 艷(1964—),女,漢族,副教授,從事常微分方程及其數(shù)值計(jì)算的研究,E-mail: sunyancust@163.com.
國家自然科學(xué)基金(批準(zhǔn)號(hào): 11171133)和數(shù)學(xué)天元基金(批準(zhǔn)號(hào): 11326209).
O241.3
A
1671-5489(2014)05-0911-05

