關(guān)于李雅普諾夫函數(shù)的幾點(diǎn)注記
徐助躍
?
關(guān)于李雅普諾夫函數(shù)的幾點(diǎn)注記
徐助躍*
(湘西自治州民族廣播電視大學(xué) 教務(wù)處, 湖南 吉首, 416000)
給出了關(guān)于李雅普諾夫函數(shù)的3個(gè)定義和3個(gè)定理, 舉例說(shuō)明了所得定義和定理的應(yīng)用, 并給出了利用廣義霍維茨條件構(gòu)造非線性系統(tǒng)李雅普諾夫函數(shù)的“三步法”.
李雅普諾夫函數(shù); 廣義霍維茨條件; 非線性系統(tǒng); 線性系統(tǒng)
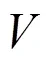
1.2 利用類函數(shù)定義函數(shù)
1.3 關(guān)于函數(shù)的幾個(gè)定理
證畢.
證法同定理1, 證明過(guò)程略.
證明 充分性證明.
必要性證明.
解 其為定正無(wú)限大函數(shù)且具有無(wú)限小上界.
解 其為定正無(wú)限大函數(shù), 但不具有無(wú)限小上界.
解 其具有無(wú)限小上界, 但不是定正的.
3 利用廣義霍維茨條件構(gòu)造函數(shù)的方法
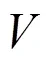
所謂霍維茨條件[12], 就是線性系統(tǒng)的特征方程的特征根都具有負(fù)實(shí)部.
考慮變量已分離系統(tǒng):
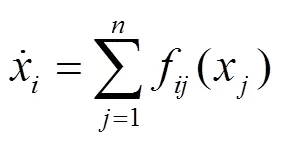
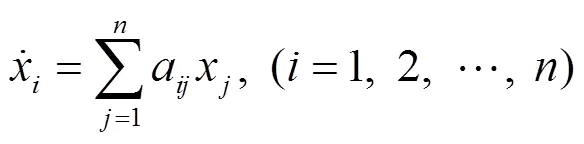
例4 考察二階非線性系統(tǒng):
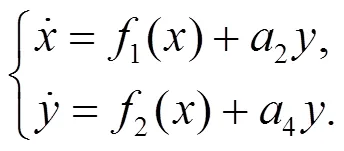
解 a. 求出線性系統(tǒng)的霍維茨條件.
對(duì)應(yīng)的線性系統(tǒng)為:
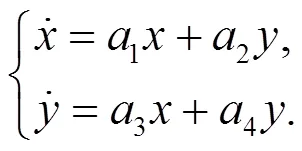
b. 求出線性系統(tǒng)的廣義霍維茨條件.
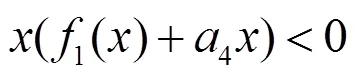
(5)式即為線性系統(tǒng)(4)的廣義霍維茨條件.
給定
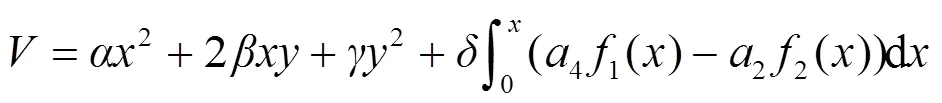
使它滿足沿系統(tǒng)(3)的導(dǎo)數(shù)為:
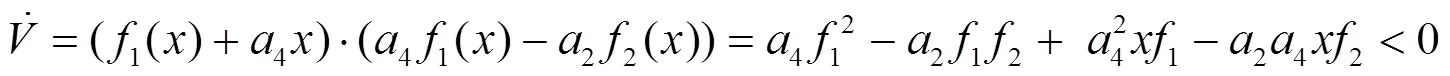
計(jì)算過(guò)程:
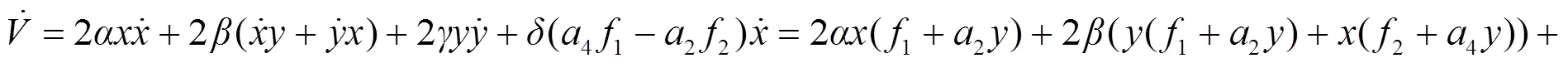
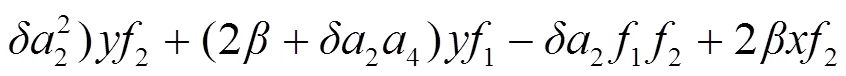
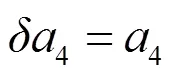
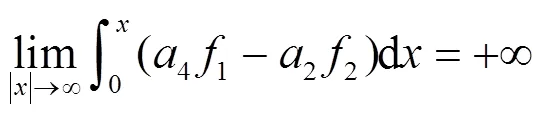
故在條件(5)和條件(9)下, 系統(tǒng)(3)的零解是全局穩(wěn)定的.
[1] 蔡燧林. 常系數(shù)線性微分方程組的Lyapunov函數(shù)的公式[J]. 數(shù)學(xué)學(xué)報(bào), 1959, 9(4): 455—467.
[2] Ponzo P T. On the stability of certain nonlinear differential equations[J]. IEEE Transactions on automatic control, 1965, 10(4): 470—472.
[3] Wall E T, Moe M L. An energy metric algorithmfor the generation of Lyapunov function[J]. IEEE Transactions on automatic control, 1968, 13: 121—122.
[4] 秦元?jiǎng)? 王聯(lián), 王慕秋, 等. 星系密度波的非線性不穩(wěn)定性[J]. 科學(xué)通報(bào), 1979, 24(16): 746—750.
[5] 秦元?jiǎng)? 王慕秋, 王聯(lián). 運(yùn)動(dòng)穩(wěn)定性理論與應(yīng)用[M]. 北京: 科學(xué)出版社, 1981: 243—267.
[6] 梁在中. 關(guān)于一類四階非線性系統(tǒng)李雅普諾夫函數(shù)構(gòu)造的研究[J]. 應(yīng)用數(shù)學(xué)和力學(xué), 1995, 16(2): 181—188.
[7] 李玉潔. 一類四階非線性系統(tǒng)的李雅普諾夫函數(shù)構(gòu)造和零解穩(wěn)定性[J]. 大學(xué)數(shù)學(xué), 2006, 22(3): 87—90.
[8] 原新生, 張懷濤. 一類三階非線性系統(tǒng)的李雅普諾夫函數(shù)的構(gòu)造[J]. 安陽(yáng)師范學(xué)院學(xué)報(bào), 2011, 13(5): 53—55.
[9] 許淞慶. 常微分方程穩(wěn)定性理論[M]. 上海: 上海科學(xué)技術(shù)出版社, 1962: 21—24.
[10] 何東武. 李雅普諾夫穩(wěn)定性理論中V函數(shù)的構(gòu)造[J]. 遼寧師范大學(xué)學(xué)報(bào): 自然科學(xué)版, 2001, 24(3): 266—271.
[11] 王聯(lián), 王慕秋. 非線性常微分方程定性分析[M]. 黑龍江: 哈爾濱工業(yè)大學(xué)出版社, 1987: 381—422.
[12] 馬爾金И Г. 運(yùn)動(dòng)穩(wěn)定性理論[M]. 解伯民, 譯. 北京: 科學(xué)出版社, 1958: 72—73.
Some notes on Lyapunov function
XU Zhu-yue
(Dean's Office, XiangXi National Radio and TV University, Jishou 416000, China)
Three definitions and three theorems of Lyapunov function were put forward, and then these definitions and theorems were illustrated with some examples. Finally, under the generalized Hurwitz condition, the "three-step method" was put forward to construct Lyapunov function of nonlinear system.
Lyapunov function; generalized Hurwitz condition; nonlinear system; linear system
10.3969/j.issn.1672-6146.2013.01.001
O 175
1672-6146(2013)01-0001-04
email: zhuyue_xu@163.com.
2013-01-10
國(guó)家開放大學(xué)立項(xiàng)重點(diǎn)科研課題(Q2705E); 湖南省科學(xué)技術(shù)廳科技計(jì)劃一般項(xiàng)目(2012FJ4334)
(責(zé)任編校:劉曉霞)

