EFFECTS OF LIQUID COMPRESSIBILITY ON RADIAL OSCILLATIONS OF GAS BUBBLES IN LIQUIDS*

ZHANG Yu-ning, LI Sheng-cai

School of Engineering, University of Warwick, Coventry, UK CV4 7AL, E-mail: Y.Zhang@warwick.ac.uk

(Received November 10, 2011, Revised July 21, 2012)

EFFECTS OF LIQUID COMPRESSIBILITY ON RADIAL OSCILLATIONS OF GAS BUBBLES IN LIQUIDS*

ZHANG Yu-ning, LI Sheng-cai

School of Engineering, University of Warwick, Coventry, UK CV4 7AL, E-mail: Y.Zhang@warwick.ac.uk

(Received November 10, 2011, Revised July 21, 2012)

For forced radial oscillations of gas bubbles in liquids, a more rigorous expression of the acoustic damping constant based on Keller?s equation is developed. Comparison with those in published papers is also made. The expression offered in this paper will improve the predictions of total damping constant in particular for high frequencies and large bubbles, i.e., large ωR0/cl(ω is the frequency of driving sound field,R0is the equilibrium bubble radius, clis the sound speed in the liquid). Examples in ultrasound imaging and acoustical oceanography are demonstrated.

gas bubble, damping constant, liquid compressibility, natural frequency

Introduction

For forced gas bubble oscillations in liquids with liquid compressibility considered, expressions of acoustic damping constant and natural frequency were derived based on radiation pressure by Chapman and Plesset[1]and Prosperetti[2]and on Keller?s equation[3]by Prosperetti[4]. These expressions are currently cited and prevalent in the literature. They are also reviewed recently by Brenner et al.[5]and Coussios and Roy[6]. However, for high frequencies and large bubbles such as those in biomedical and oceanic applications, a more rigorous expression of acoustic damping constant has been derived by the authors based on Keller?s equation. The reasons for the improvements by using our expressions in those areas are discussed as well.

1. Derivation based on Keller’s equation

In this section, expressions for damping constants and natural frequency will be derived based on Keller?s equation. Prosperetti and Lezzi[7]proposed aone-parameter family of equations of bubble radius to the first order of bubble-wall Mach number, which treats Keller?s equation as a special case. For small oscillations considered in the present paper, expressions of acoustic damping constant and natural frequency will be the same for equation of bubble motion which falls into this one-parameter family (referring to Appendix). Here, a more appropriate expression of Keller?s equation was used[7,p.466]. Here, oscillations of spherical gas bubbles with small amplitude in infinite liquids are considered. Keller?s equation[3,7]can be written as

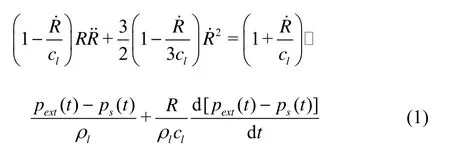
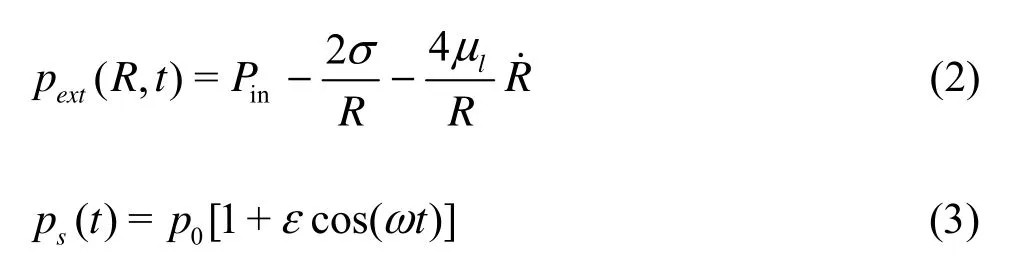
wherehere R is the instantaneous bubble radius and the overdot denotes its time derivative, clis the speed of sound in the undisturbed liquid[7],ρlis the liquid density, t is the time,Pinis the pressure at the gas side of the bubble wall, σ is the surface tension,μlis the viscosity of the liquid, p0is the ambient pressure, ε is the non-dimensional amplitude of driving sound field, ω is the frequency of driving sound field.

For comparison, the framework in Ref.[2] for thermal effects will be followed but the equation based on radiation pressure (Prad) replaced by Keller?s equation. Notations in Ref.[2] will also be retained the same such as

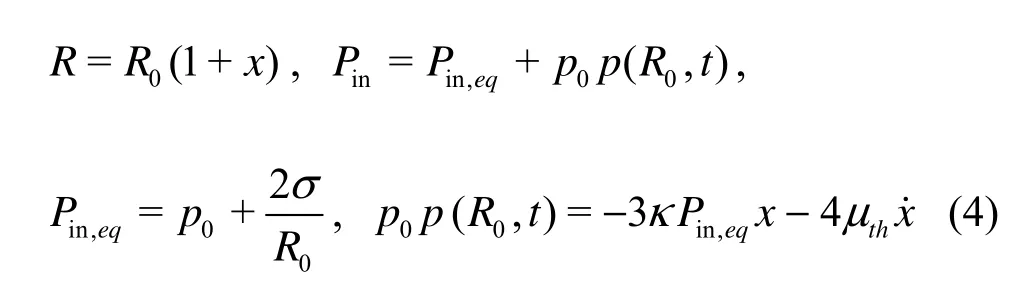
Here R0is the equilibrium bubble radius,x is the non-dimensional perturbation of instantaneous bubble radius, p(R0,t ) the non-dimensional pressure deviation from equilibrium pressure,Pin,eqthe equilibrium pressure in the gas, μththe effective thermal viscosity, κ the polytropic exponent. When the acoustic wave is weak (εg1), the amplitude of the bubble oscillation is small (xg1). Substituting above relations into Eq.(1) and omitting the 2nd and higher orders ofx (or ε) result in an inhomogeneous equation for a harmonic oscillator i.e., the oscillating bubble being studied,

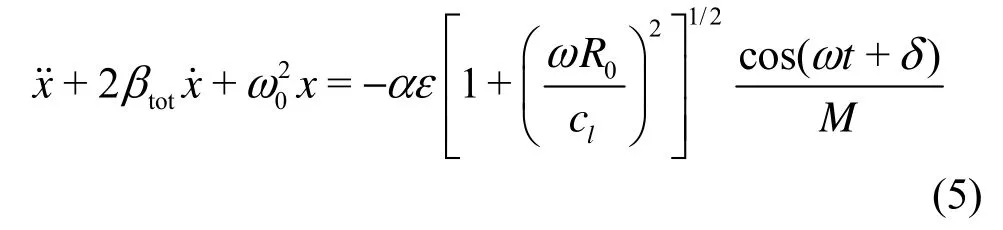
where

In Eq.(5), βtotis the total damping constant, ω0is the natural frequency. The total damping constant (βtot) is

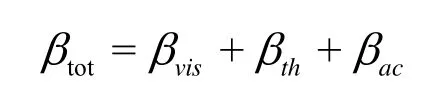
where

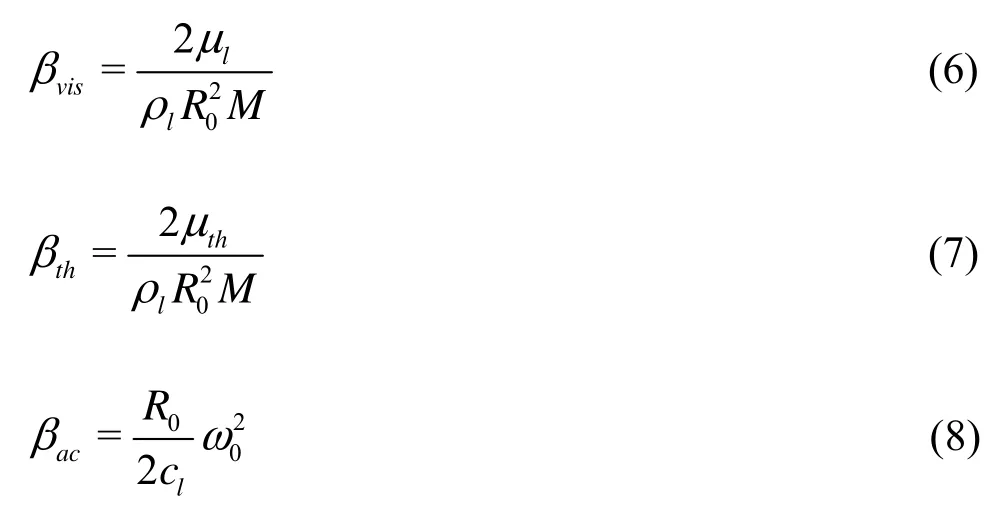
represent the viscous, thermal and acoustic damping constants respectively. The natural frequency of the harmonic oscillator is

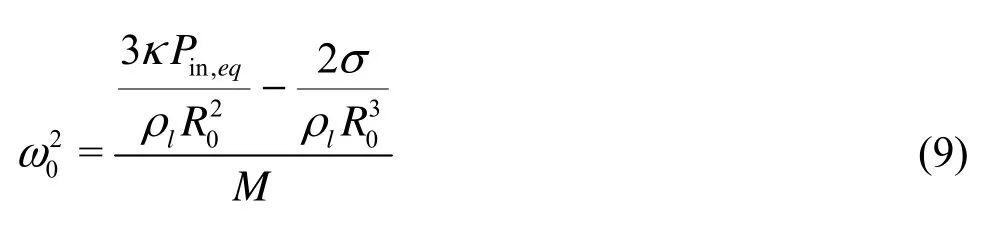
Note that herelμ,thμ and liquid compressibility make contributions to natural frequency through M in Eq.(9) though these contributions are relatively small. Taking an air bubble oscillating in water as an example, M varies between 1 and 1.03 if10-2m≥R≥10-7mand 108s-1≥ω≥104s-1.

0Forced oscillations of bubbles will enter stationary oscillations once the transient term (i.e., the complementary function or the solution for the corresponding homogenous equation) in the solution approaches to zero. For most cases of bubble oscillations, this contribution from the transient term decays quickly. For example, for a bubble of radius 1 μm driven by an external force at the frequencyω=107s-1with the non-dimensional amplitude ε=0.1, the ratio of amplitudes between the transient term and the stationary term (i.e., the particular integral for the inhomogeneous equation) reduces down to 0.1 att= 1.15 μs. Therefore, for many applications where the transient term approaches to zero quickly, the oscillation to be analyzed can be simplified as a stationary one such as appearing in the previous studies. Here, for the stationary forced oscillations driven by sound field of single frequency (ω),μthin Eq.(7) andκ in Eq.(9) can be determined by solving the bubble interior problem following the approach in Ref.[2]. Though Keller?s equation has been used in this paper to replace the equation based on the radiation pressure as used by Prosperetti[2], the resultant expressions for μthand κ are the same noticing that expressions of μthand κin Ref.[2] were determined by comparing solutions of two methods: one based on the polytropic model with effective thermal damping, the other based on solution of bubble interior.

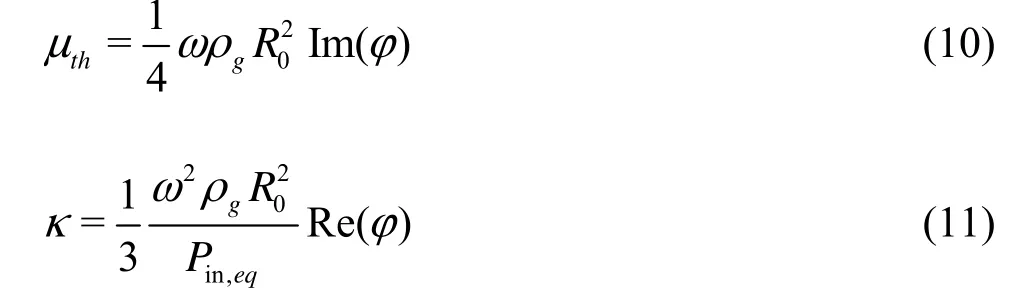
Here φ is a function relating to the solution of the bubble interior problem (Eqs.(16) and (17) of Ref.[2]). Note that the recent study by Zhang and Li[8]pointed out that the approximation of G1≈0 where G1is a non-dimensional parameter employed in Ref.[2] and reflects the length ratio between the mean free path and the wavelength in gas should be dropped off if G1≥10-2. As to the valid regions for the frame work of Prosperetti[2], readers are referred to Ref.[8] that categorized the bubble behavior into three different regions according to the ratios of the bubble radius to the wavelengths in gases and liquids.

Thus,Eq.(5) reduces to

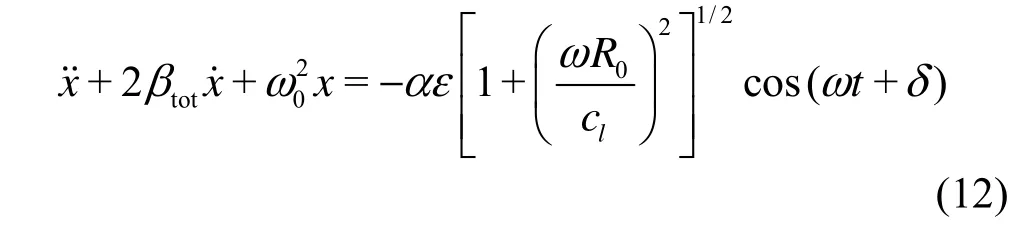
Here ω0and βtotreduce to

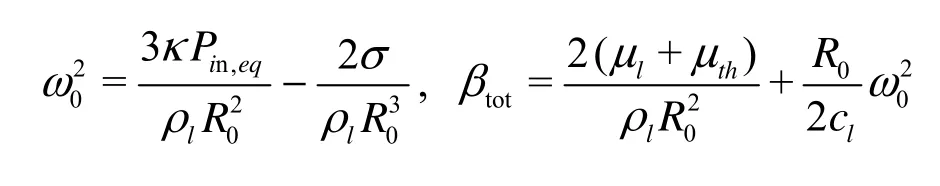
The expression for natural frequency is well cited, in which the contribution of compressibility (through M) disappears. However, the contribution of compressibility to the total damping constanttotβ does not disappear completely since theacβ term still remains.

Furthermore, if cl→∞ (corresponding to/ cland R0/cl→0), i.e., for incompressible cases, Eq.(1) reduces to the Rayleigh-Plesset equation. And Eq.(12) reduces to

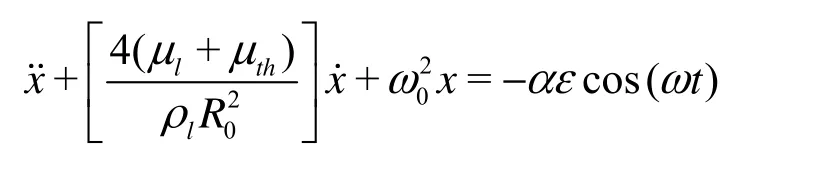
identical to the cases where the Rayleigh-Plesset equation replaces the radiation pressure in Ref.[2]. Naturally, the acoustic damping disappears since liquid compressibility is not considered in the Rayleigh-Plesset equation.

2. Comme nts on published expressions

In order to compare with those published expressions, complex analysis is used in this section and Eqs.(3) and (5) become

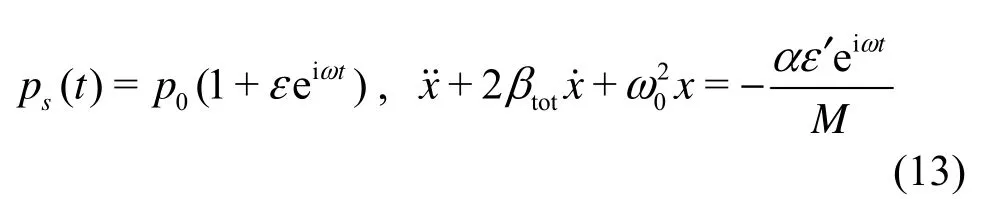
where

Firstly, we discuss tho se published papers based on Keller?s equation. If we follow Prosperetti[4], dividing Eq.(13) by (1+ωR0/cl), neglecting all terms with order of c-2and using ˙x=iωx˙ and x˙= iωx[4,p.72], Eq.(13) becomes

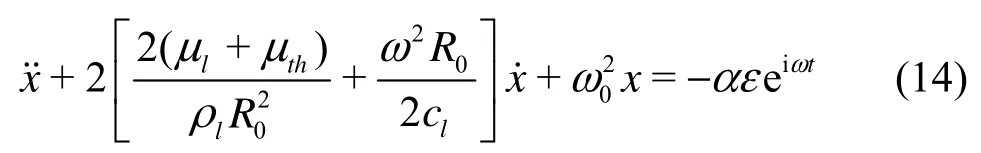
This is just the Eqs.(29)-(30) in Prosperetti[4]. The acoustic damping constant (ω2R0/2cl)shown in Eq.(14) is different from ours, i.e.,ω02R0/2clof Eq.(8), by noticing that ω≠ω0for no n-resonant oscillations. This also explains why the prediction of acoustic damping constant can be improved by using our approach for high frequencies and large bubbles because for those cases the decreasing ω0is further deviating from the increasing ω. Indeed, the approach employed in Ref.[4] as demonstrated above can be avoided. Instead, the expressions of damping and natural frequency can be determined directly from the coefficients of the harmonic oscillator based on the linearization of Keller?s equation. The term (1+ iωR0/cl) can still remain on the right hand sideof Eqs.(5) and (13), without using the relations of ˙x= iωx˙ and x˙=iωx. This is exactly the approach employed for the derivations of damping constants and natural frequency in Section 1. Furthermore, only for oscillations entering the stationary phase, the transient term disappears from the solution such that ˙x=iω x˙ and˙=iωx (referring to Section 1). Nevertheless, to bestrictly speaking, these two relations should not be used for the purpose of determining the expressionsof damping constants and natural frequency. Otherwise, they would have changed the coefficients of this inhomogeneous second-order equation that represent the damping constants and natural frequency of the harmonic oscillator defined by this equation (Eq.(5) or Eq.(13)). For demonstrating examples, readers are referred to the following parts of this paper. Consequently, the resultant expressions defined by Eq.(14) will deviate from the true damping constants and natural frequency.

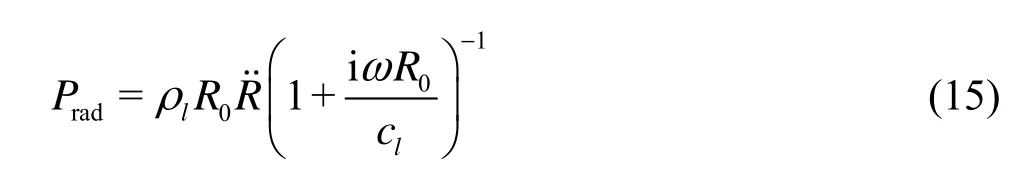
Now, we turn our attention to those expressions based on radia tion pressure, e.g., in Ref.[2], For more original studiesrelating to the use of radiation pressure, readers are referred to the list of references given in Ref.[2]. Then one can obtain as in Ref.[2],

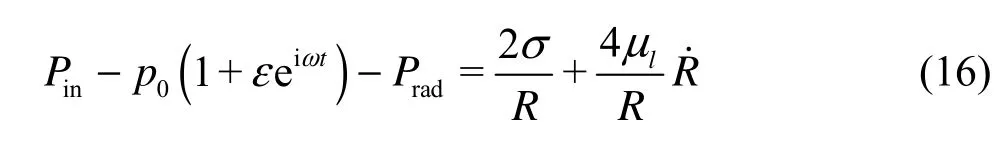
Substituting Eqs.(4) and (15) into Eq.( 16) yields

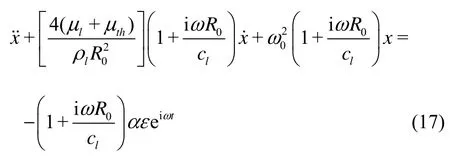
In order to demonstrate how the expressions in those literatures were reached, the relations of˙x=iωx˙and x˙=iωx are to be employed, which will lead to variable expressions for “natural frequency” and “damping constants” as shown below.

If both sides of Eq.(17) divided by (1+iωR0/ cl), it becomes

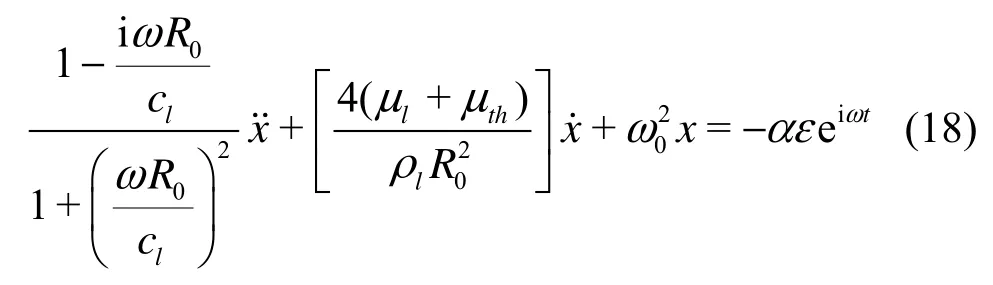
The first term in Eq.(18) then is rearranged using˙= iωx˙as

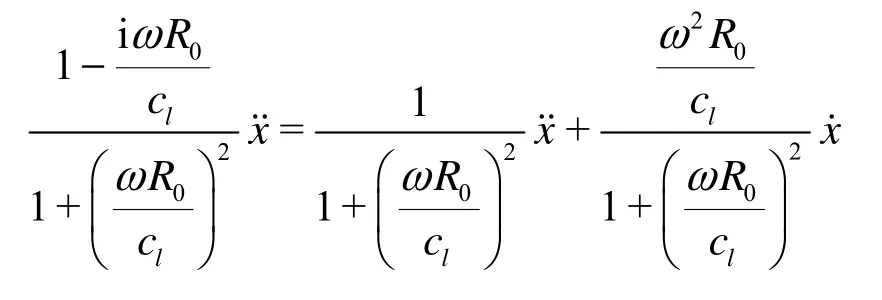
Substituting it into Eq.(18) leads to

If all terms with order of c-2are neglected in Eq.(19), this will yield the acousticdamping constant as expressed by Eq.(27) in Ref.[1].For completeness, all terms with order of c-2are kept in the following derivations.

Following Prosperetti[2], if the first term in Eq.(19) is further treated by using the relations of ˙x=iω x˙ and x˙=iωx, i.e.,

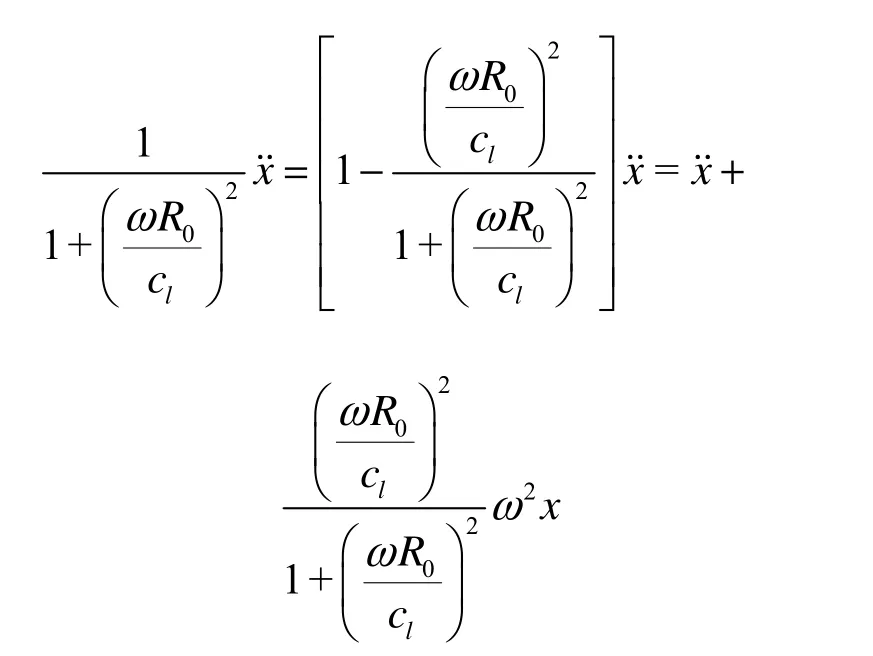
Equation (19) will again become another inhomogeneous 2nd order equation withdifferent coefficients,

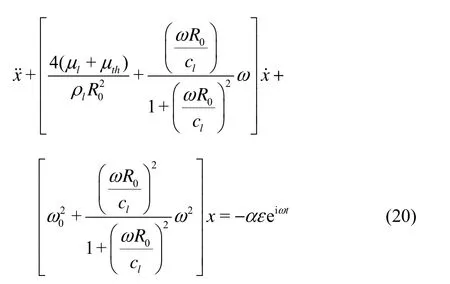
This is just the equation used for determining the expressions of damping and natural frequency in Ref.[2].

The above demonstration shows how the use of ˙x=iω x˙and x˙=iω xchanges the coefficients of the equation, resulting in various different expressions for the natural frequency and damping constants of theharmonic oscillator as appeared in the literatures such as the cont radiction between those two groups of published studies represented by Eqs.(19) and (20) respectively. It also explains why there is a difference between Prosperetti?s[4]and ours.

3. Comparisons

The expression of acoustic damping constant derived by us is different from those by Chapman and Plesset[1]and Prosperetti[2,4]. For natural frequency, our expression is almost identical to theirs except for Prosperetti[2]. Therefore, a comparison with Ref.[2] should be essential. The slight difference of acoustic damping between Eq.(19) and Eq.(20), i.e., (ωR0/ cl)2, is trivial and excluded from discussions. The assumption of spherical bubble (i.e., uniform pressure outside bubble when R0/λl＜0.1, where λlis wavelength in liquids) limits the value of ωR0/cl(i.e., 2πR0/λl) up to 0.628, referring to Ref.[8]. Therefore, those bubbles within this range are to be considered in the following discussions.

1(a) ω=104s-1

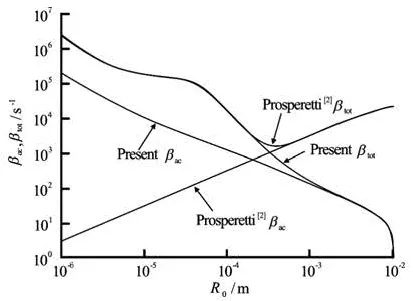
1(b) ω=105s-1

In this section, values predicted by Prosperetti[2]based on radiation pressure will be compared with ours. Forced oscillations of air bubbles in water will be considered with the same properties as in Ref.[2] if no t specified. The value of klandDgin Prosperetti[2,p.27]have typographical errors and sh ould be 0.59J/m·s·K and 0.2912 m2/s (5.9× 104erg/cm·s·K and 0.2912 cm2/s) respectively. Dgin Prosperetti[2,p.19]was defined using constant volume, which is correct. However, the value ofgD in Prosperetti[2,p.27]was using constant pressure, which should be Dg/γ (γ is specific heat ratio). In figures, “Prosperetti[2]” refers to Eq.(20) based onradiation pressure and “Present” refers to Eqs.(6)-(9) based on Keller?s equation deri- ved by us. To focus on liquid compressibility, natural frequency, acoustic and total damping constants are compared.

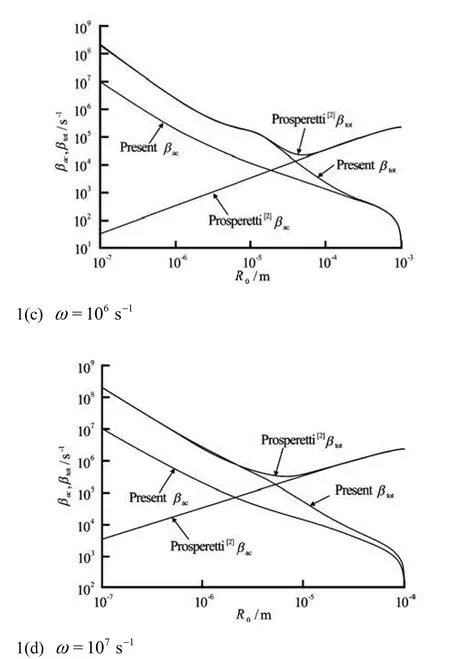
Fig.1 Comparison of acoustic and total damping constants (βacand βtotrespectively) between Prosperetti?s[2]andours (present)

Figures 1 and 2 show the comparisons of the acoustic and thetotal damping constants and the natural frequencies for ω=104s-1, 105s-1, 106s-1and 107s-1respectively. These comparisons demonstrate that the acoustic damping constants predicted by us are quite different from those in Ref.[2]. For the total damping constant and the natural frequency, our pre-

dictions are much smaller than those by Prosperetti[2]in particular for large ωR0/clthat is the region where the ultrasound induced bubbles are currently widely used in oceanic and biomedical applications. For gas bubble oscillating in liquids, in order to limit the error of prediction within a reasonable range, our approach should be employed for predicting total damping constants and natural frequency if ωR0/clis large.

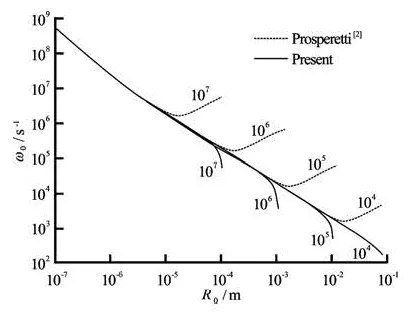
Fig.2 Comparison of naturalfrequency between Prosperetti?s[2]and ours. The labeledvalues are ω (s-1)

4. Application example s

Acoustic damping and natural frequency are fund amental issues for gasbubbles oscillating in liquids. The findings presented in this paper are thus essential for many circumstances. Only a few of them are briefly mentioned here as examples. It should beemphasized that the present findings are only valid for the oscillations of spherical gas bubbles. For non-spherical bubble dynamics, more sophisticated model (e.g., the direct numerical simulation developed by Tryggvason and coworkers[9]) should be employed. For some recent progress in this subject, readers are referred to Chen et al.[10]and Zhang and Li[11].

Typical cases in medical applications (e.g., contrast agent in diagnostic ultrasound imaging, gene therapy and drug delivery) are of bubble size 1 μm-10 μm and driving frequency 1.5 MHz-15 MHz[12], corresponding to ωR0/clranging between 0.00628 and 0.628. In this region, the difference between ours and published studies is noticeably large. Currently, problems with even higher frequencies (up to 30 MHz or above), e.g., ultrasonic wave propagation in dilute bubbly mixture[13], are of interest. For more examples, readers are referred to our earlier paper[8]as well as other recent publications[14].

The other example is the absorption and extinction cross sections (aσ andeσ) of forced bubble oscillations, which were determined by Medwin and Clay[15]as

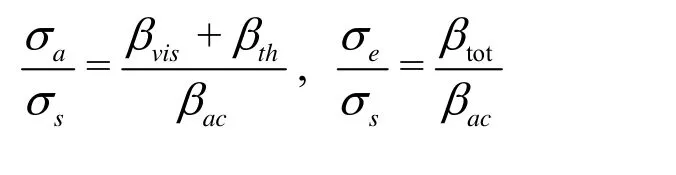
wheresσ is the acoustical scattering cross section. Therefore, the prediction of acoustic damping will significantly affect the values of σ and σ.

a

e

5. Conclusion

For forced gas bubble oscillations in liquids, a more rigorous expression of acoustic damping has been developed based on Keller?s equation. The difference between the published literatures and ours is mainly owing to the use of the relations ˙x=iωx˙and x˙=iωx. This correction to the published papers is essential when high frequencies and large bubbles (i.e., largeωR0/cl) are involved such as those acoustic bubbles in biomedical and oceanic applications.

Acknowledgements

This work was supported by the UK EPSRC WIMRC (Grant No. RESCM 9219) the EPSRC WIMRCPh.D. studentship (Grant No. RESCM 9217).

[1]CHAPMAN R. B., PLESSET M. S. Thermal effects in the free oscillations of gas bubbles[J]. Journal of Basic Engineering, 1971, 94: 142-145.

[2] PROSPERETTI A. Thermal effects and damping mechanisms in the forced radial oscillations of gas bubbles in liquids[J]. Journal of the Acoustical Society of America, 1977, 61(1): 17-27.

[3] KELLER J. B., MIKSIS M. Bubble oscillations of large amplitude[J]. Journal of the Acoustical Society of America, 1980, 68(2): 628-633.

[4]PROSPERETTI A. Bubble phenomena in sound fields: Part one[J]. Ultrasonics, 1984, 22(2): 69-77.

[5] BRENNER M. P., HILGENFELDT S. and LOHSE D. Single-bubble sonoluminescence[J]. Reviews of Modem Physics, 2002, 74(2): 425-484.

[6] COUSSIOS C. C., ROY R. A. Applications of acoustics and cavitation to non-invasive therapy and drug delivery[J]. Annual Review of Fluid Mechanics, 2008, 40: 395-420.

[7] PROSPERETTI A., LEZZI A. Bubble dynamics in a compressible liquid. Part 1. First-order theory[J]. Journal of Fluid Mechanics, 1986, 168: 457-478.

[8]ZHANG Y., LI S. C. Notes on radial oscillations of gas bubbles in liquids: Thermal effects[J]. Journal of the Acoustical Society of America, 2010, 128(5): EL306-EL309.

[9]TRYGGVASON G., SCARDOVELLI R. and ZALESKI S. Direct numerical simulations of gas-liquid multiphase flows[M]. New York: Cambridge University Press, 2011, 133-160.

[10] CHEN Hui, LI Sheng-cai and ZUO Zhi-ga ng et al. Direct numerical simuiation of bubble-cluster?s dyna-mic characteristics[J]. Journal of Hydrodynamics, 2008, 20(6): 689-695.

[11] ZHANG Yu-ning and LI Sheng-cai. Direct numerical simulation of collective bubble behavior[J]. Journal of Hydrodynamics, 2010, 22(5 Suppl.): 827-831.

[12]SZABO T. L. Diagnostic ultrasound imaging: Inside out[M]. London: Elsevier Academic Press, 2004, 455-488.

[13]ANDO K., COLONIUS T. and BRENNEN C. E. Improvement of acoustic theory of ultrasonic waves in dilute bubbly liquids[J]. Journal of the Acoustical Society of America, 2009, 126(3): EL69-EL74.

[14]MIRI A. K., MITRI F. G. Acoustic radiation force on a spherical contrast agent shell near a vessel porous walltheory[J]. Ultrasound Medicine and Biology, 2011, 37: 301-311.

[15] MEDWIN H., CLAY C. S. Fundamentals of acoustical oceanography[M]. San Diego, USA: Academic Press, 1998, 302-304.

Appendix

In this appendix, the influences of one-parameter familyequation on the expressions of damping and natural frequency for the radial oscillations of gas bubbles in liquids are discussed. Prosperetti and Lezzi[7]proposed the followingone-parameterfamily equation (general Keller-Miksis equation) if written in terms of pressure

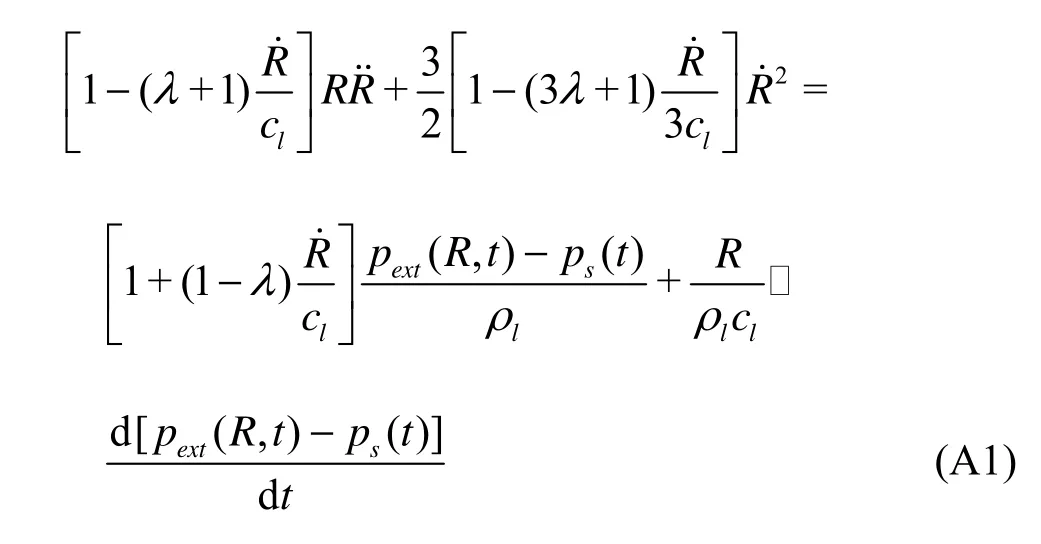
whereλis an arbitrary parameter which is of smaller order of1/Ma(Mais the bubble wall Machnumber)[7,p.466andEq.(4.3)], pext(R,t) andps(t) are given by Eqs.(2) and (3) respectively. If λ=0, Eq.(A1) reduces to Keller?s equation (i.e., Eq.(1)).

The procedure of derivations of damping constants and natural frequency for linear gas bubble oscillations in liquids based on Eq.(A1) are exactly the same as those based on Keller?s equation. Here, we will only keeps terms up to second order of ε (or x). Substituting R=R0(1+x)into terms related withλ in Eq.(A1), we obtain

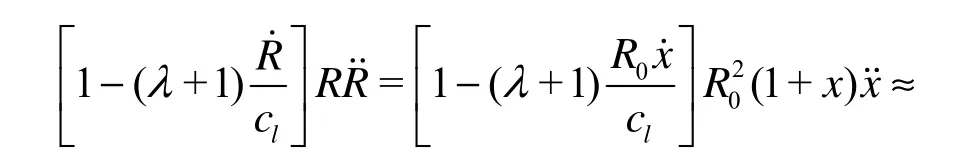
From Eqs.(A2)-(A4), it is clearly seen that terms involvingλin Eq.(A1) are all of the second or higher orderof ε (orx). Therefore, for linear oscillations (up to the 1st order ofx), all the equations falling in this one-parameter family equation of bubble motion will give the same expressions for damping constants and natural frequency as those shown in this paper.

10.1016/S1001-6058(11)60301-6

* Biography: ZHANG Yu-ning (1983-), Male, Ph. D. Candidate

LI Sheng-cai,

E-mail: S.Li@warwick.ac.uk