一類具有正負系數(shù)一階中立型微分方程的振動性

石艷香,劉桂榮

一類具有正負系數(shù)一階中立型微分方程的振動性

石艷香1,2,劉桂榮2

(1.廣州大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院,廣東廣州510006;2.山西大學(xué)數(shù)學(xué)科學(xué)學(xué)院,山西太原030006)

考慮一類具有正負系數(shù)一階中立型微分方程

建立該方程一切解振動的兩個充分性條件.

中立型微分方程;振動性;最終正解

本文考慮一類具有正負系數(shù)一階中立型微分方程

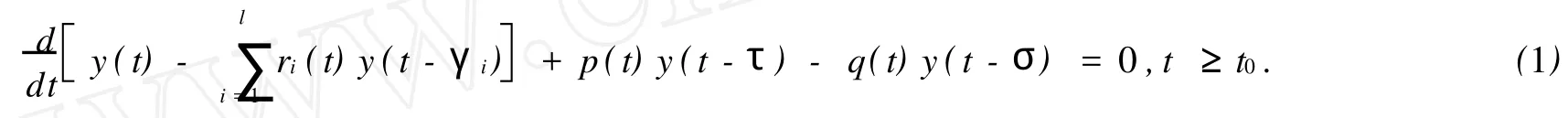
總假定

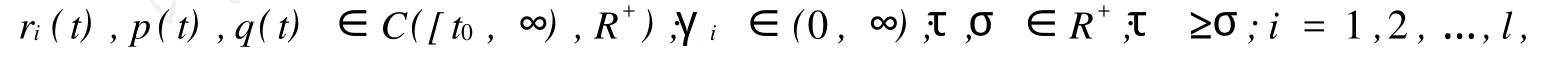
并且p(t)-q(t-τ+σ)≥0且最終不等于零.本文的目的是建立方程(1)所有解振動的新的充分性條件.

對方程(1),當(dāng)i=1時的振動性已經(jīng)有了許多不同的充分性判斷[1,3-5].在文[1]中作者對以下方程

給出了其振動的充分性條件.顯然問題(2)是問題(1)的特例.需要強調(diào)的是,在本文中,運用文[2]的方法給出方程(1)振動的新的充分性條件,所得的結(jié)論與由方程(2)直接推廣到方程(1)所得的結(jié)論相比,前者要弱.

方程(1)的解稱為振動,如果它的解有充分大的零點;稱為非振動,如果它的解最終正或最終負.

引理 (A1)假設(shè)存在θ∈(0,1],使得

若y(t)是方程(1)的一個最終正解,且設(shè)

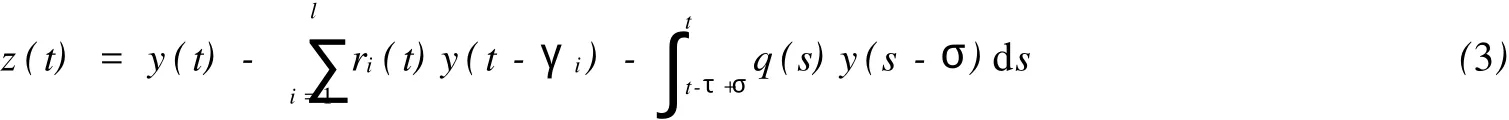
則z′(t)≤0,z(t)>0.

證明 從方程(1)和式(3),有

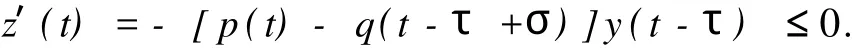
下證z(t)>0.假設(shè)z(t)<0,那么存在T≥t0和β<0,滿足:z(t)<β<0,t≥T.因此由(3)和已知條件有

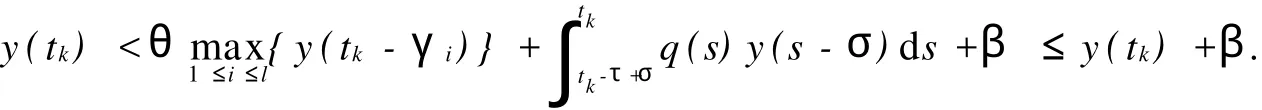
得到矛盾.

對上式取上極限,當(dāng)k→∞時,有

得到矛盾.故z(t)>0.引理得證.

下面給出本文的主要結(jié)論.

定理1 假設(shè)條件(A1)成立,且

(A2)p(t)>0,q(t)>0,且

(A3)存在函數(shù)αi(t)∈C([t0,+∞],R+)(i=1,2,…,l)滿足:

(A4)存在正連續(xù)函數(shù)

則方程(1)的所有解振動,如果存在T,當(dāng)t≥T時,下列任意一個條件成立:

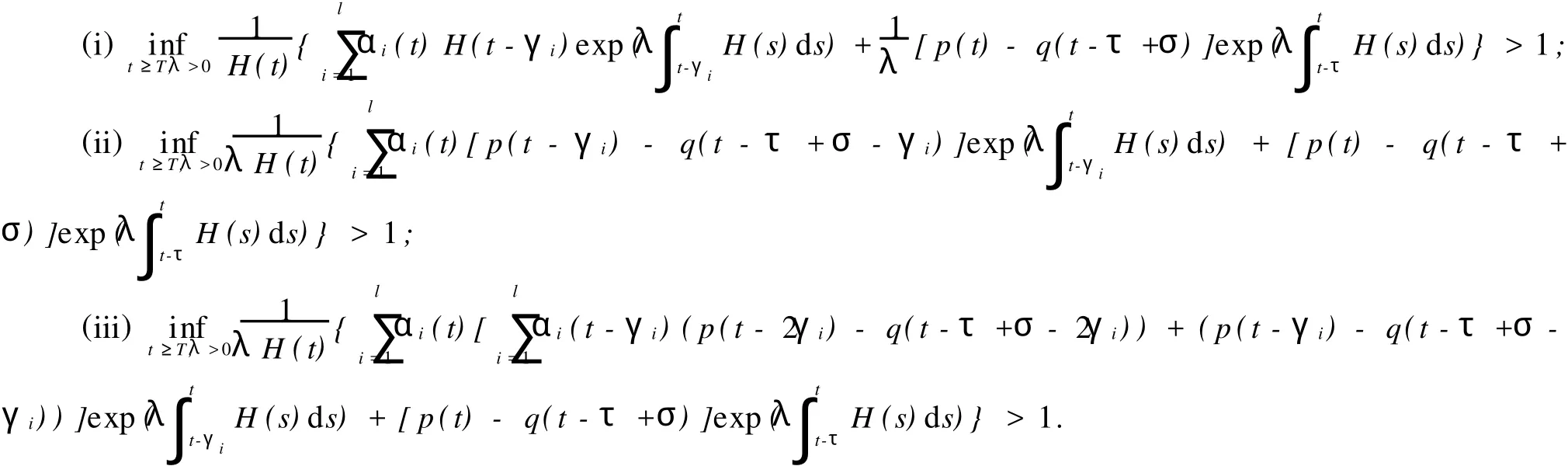
證明 否則,若方程(1)有一個最終正解y(t),設(shè)z(t)如(3)式,則由引理得z(t)>0,z′(t)≤0.且z(t)≤y(t),當(dāng)t≥T1≥t0.由方程(1),條件(A2),(A3),有

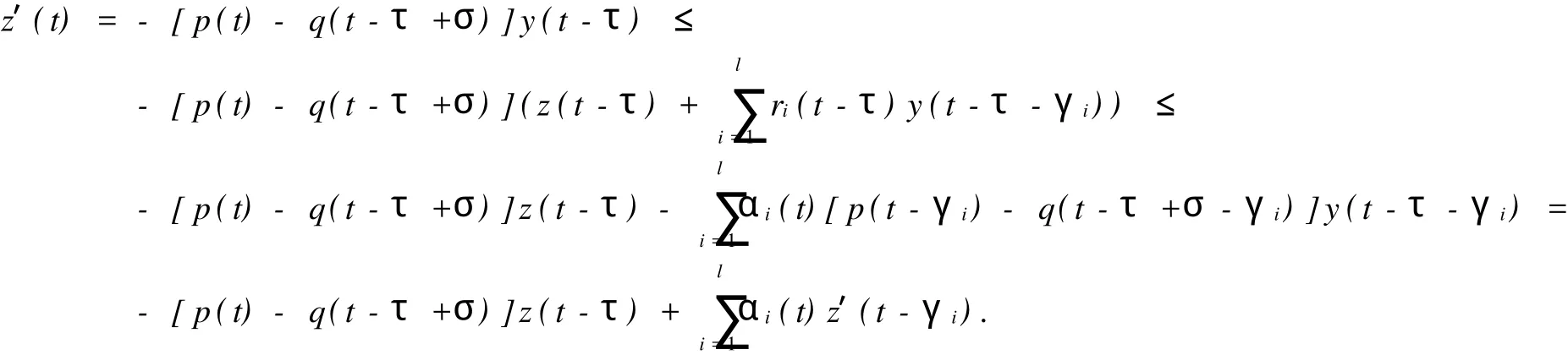
即

設(shè)

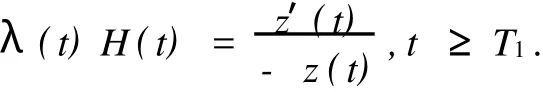
則λ(t)>0.由(5)式可以誘導(dǎo)出

(I)條件(i)成立,存在一個δ∈(0,1)滿足

另一方面,由文[6](引理2.1),(A2)和(7)式,有

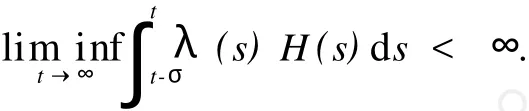
由(A4)知事實上,則存在一個點列,滿足tk≥ max{T1,T}+max{γ,τ},且令λ(tk)=min{λ(t),t∈[T1,tk]},k=1,2,…,從(6)式有

則當(dāng)s≥T2,有

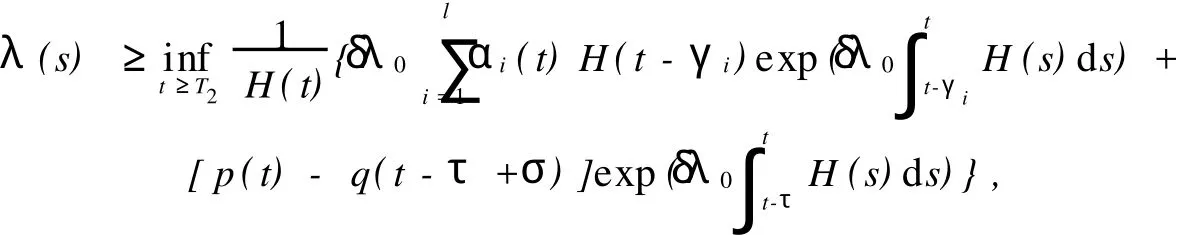
對s取下極限,有

令δ λ0=λ1,有

因為T2≥T,λ1>0,則(9)式與(8)式矛盾.

(II)條件(ii)成立,由(6)式,有λ(t)H(t)≥p(t)-q(t-τ+σ),則代入(6)式,有

類似于(I)的證明,如果條件(ii)滿足,從(10)式可以完成證明;如果條件(iii)滿足,從(11)式可以完成證明.定理得證.

由于ex≥ex,且ex>1,x>0,我們從定理1得到下面推論.

推論1 假設(shè)條件(A1)-(A4)成立,且

則方程(1)的所有解振動.

定理2 假設(shè)條件(A1)-(A4)成立,且

(A5)令hi(t)=t-γi,g(t)=t-τ,t≥t0,i=1,2,…,l.

則方程(1)的所有解振動,如果存在T,當(dāng)t≥T時,下列任意一個條件成立:

證明 否則,若方程(1)有一個最終正解y(t).類似于定理1的證明過程,可以推導(dǎo)出:

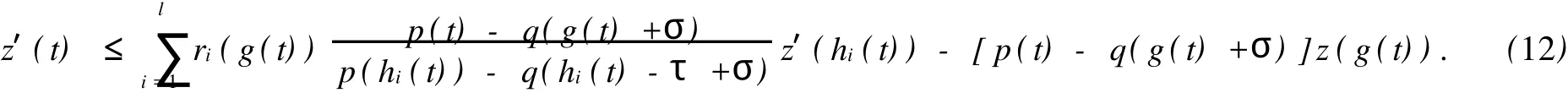
令

則λ(t)>0,且由(12)式可以推導(dǎo)出

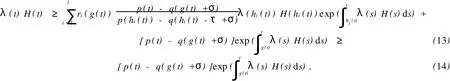
從(14)式,有λ(t)H(t)≥p(t)-q(g(t)+σ),代入(13)式有,

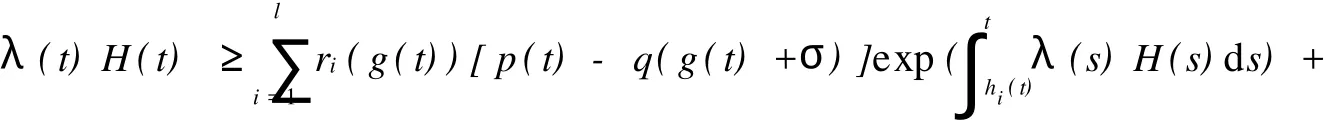
類似于定理1的證明,如果條件(i)滿足,從(13)式可以完成證明;如果條件(ii)滿足,從(15)式可以完成證明.定理得證.

類似于推論1,我們從定理2得到下面推論.

推論2 假設(shè)條件(A1)-(A5)成立,且

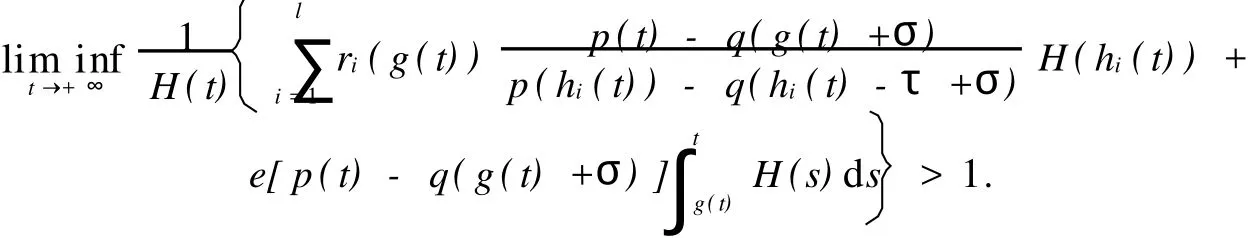
則方程(1)的所有解振動.

注 本文得到的兩個充分性條件以及兩個充分性推論是對文[1]中研究的方程的推廣:文[1]關(guān)于方程(2)的振動結(jié)果都需要如下的假設(shè)條件:

這是一個充分條件,本文在不需要上述條件的情況下建立方程(1)振動的新的充分性條件.同時,本文對文[2]進行了改進,文[2]中當(dāng)l=2時給定的系數(shù)都是正的,而本文研究的方程既有正系數(shù),也有負系數(shù).

[1] SHEN J H,DEBNATH L.Oscillations of Solutions of Neutral Differential Equations with Positive and Negative Coefficients[J].A pplied Mathematics Letters,2001,14:775-781.

[2] WANG Qi-ru.Oscillation Criteria for First-order Neutral Differential Equations[J].A pplied Mathematics Letters,2002 (15):1025-1033.

[3] WANG Qi-ru.Oscillation Theorems for First-order Nonlinear Neutral Functional Differential Equations[J].Computers Math A ppl,2000,39(5/6):19-28.

[4] FARREL K,GROVE E A,LADAS G.Neutral Delay Differential Equations with Positive and Negative Coefficients[J]. A ppl A nal,1988,27:181-197.

[5] LALLI B S,ZHANGB G.Oscillation of First order Neutral Differential Equations[J].A ppl A nal,1990,39:265-274.

[6] GYORI L.On the Oscillatory Behavior of Solutions of Certain Nonlinear and Linear Delay Differentail Equations[J].Nonlinear A nal,1984,8(5):429-439.

two sufficient conditions are obtained for oscillation of all solutions of the neutral equation.

Oscillation of the First Order Neutral Differential Equation with Positive and Negative Coefficients

SHI Yan-xiang1,2,LIU Gui-rong2
(1.School of Mathematics and Inf ormation Sciences,Guangzhou University,Guangzhou510006,China; 2.School of Mathematical Sciences,Shanxi University,Taiyuan030006,China)

neutral differential equation;oscillation;eventually positive solution

For the first order neutral differential equation with positive and negative coefficients

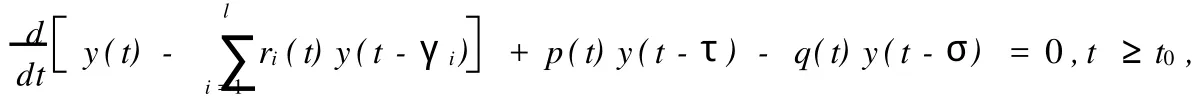
O175

A

0253-2395(2010)02-0161-05