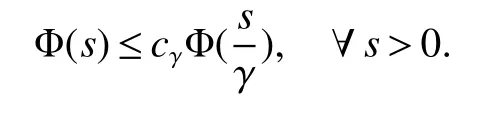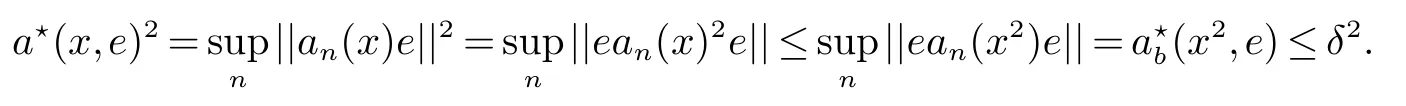Individual Ergodic Theorems for Noncommutative Orlicz Space?
Sajida Turgun,Turdebek N Bekjan
(College of Mathematics and System Sciences,Xinjiang University,Urumqi,Xinjiang 830046,China)
Abstract: Let(M,τ)be a semifinite von Neumann algebra and Φ be an N-function.We proved individual ergodic theorem in the noncommutative Orlicz space LΦ(M).
Key words:Noncommutative orlicz space,Individual ergodic theorem,Uniformly equicontinuous in measure
0 Introduction
Using the operator space theory and theory of interpolation of Banach spaces,Junge and Xu[1]proved a noncommutative analogue of the classical Dunford-Schwartz maximal ergodic inequality for positive contraction onLp,and the analogue of Stein’s maximal inequality for symmetric positive contractions onLp,1 The purpose of this article is to present the individual ergodic theorems in the noncommutative Orlicz spaceLΦ(M)associated with semifinite von Neumann algebra(M,τ)and N-function Φ. The article is organized as follows.Section 1 contains some preliminaries and notations on the noncommutative Orlicz-spaces and noncommutativeLp-spaces,in section two we give some theorems,definitions about uniform equicontinuity of sequences of operators.Finally,using the technics in[3]we prove the individual ergodic theorems in Non-commutative Orlicz spacesLΦ(M). In this section,we collect some basic facts and notion that will be used for what follows.Throughout this paper,we denote by M a semifinite von Neumann algebra acting on a Hilbert space H,with a normal semifinite faithful trace τ.LetP(M)be the complete lattice of all projections in M.A densely defined closed operatorxin H is said to be affiliated with M ifyx?xyfor everyy∈ M,where Mis the commutant of the algebra M.An operatorx,affiliated with M,is said to be τ-measurable if for each ε >0 there existse∈P(M)with τ(e⊥)≤ ε such thate(H)?D(x),wheree⊥=I?e,Iis the unit of M,D(x)is the domain of definition ofx,letL0(M)be the set of all τ-measurable operatorsaffiliated with M,let||·||stand for the uniform norm in M.The measure topology inL0(M)is given by the system of neighborhoods of zero.For a positive self-adjoint operatorλdeλaffiliated with M one can define If 1≤p<∞,then the noncommutativeLp-space associated with(M,τ)is defined as Let S+(M)={x∈M+:τ(s(x))<∞}and S(M)is linear combination of S+(M).We will often denote S+(M)and S(M)simple by S+and S,respectively. Letxbe a τ-measurable operator andt>0.The “tth singular number(or generalizedsnumber)ofx” μt(x)is defined by See[4]for more information about generalizedsnumber. We remark that ifx∈L0(M),then (i)Φ is even and convex, (ii)Φ(x)=0 iffx=0, An N-function Φ is said to obey the2-condition for allt,written often as Φ ∈2,if there isk>2 such that Φ(2t)≤kΦ(t)for all t≥0.Indices of an N-function Φ are provided by the following two constants, where ?(t)is the left derivative of Φ(t)(See[5]for more information about N-function). Definition 1Let M be a semifinite von Neumann algebra,Φ is N-function,the noncommutative Orlicz spaceLΦ(M)is defined by LetXbe any set,ifwe denote Definition 2Let(X,||·||)be a normed space andX0is a subset ofXsuch that 0 ∈X0,where 0 is the neutral element ofX.A familyai:X→L0(M),i∈I,of additive maps is called uniformly equicontinuous in measure(u.e.m)(bilaterally uniformly equicontinuous in measure(b.u.e.m))at 0 onX0,if,given ε >0,δ >0,there is such γ >0 that for everyx∈X0with||x||<γ there existse∈P(M)for which Let a positive linear map α :L1(M)→L1(M)be such that α(x)≤ 1 and τ(α(x))≤ τ(x)for everyx∈L1(M)∩M with 0≤x≤1.Note that,as it is shown in[2],there exist unique continuous extensions α:Lp(M)→Lp(M)for every 1≤p<∞ and a unique ultra-weakly continuous extension α:M→M.Let Φ be an N-function with 1 Lemma 1Let Φ be an N-function.Ifan:LΦ(M)→L0(M),n=1,2,...,then the family{an}is u.e.m.(b.u.e.m.)at 0 on(LΦ(M),||·||Φ)if and only if it is u.e.m.(respectively,b.u.e.m.)at 0 on(LΦ+(M),||·||Φ). ProofLet us consider the bilateral case.the “only if” part is obvious.To prove the “if” part,fix ε >0 and δ >0.Then there is such aimply that Takex∈LΦ(M)such that||x||Φ< γ.Then we can writesuch thatOn the other hand, Therefore,x1≤ |x1?x2|,x2≤ |x1?x2|,it follows thatμt(x1)≤ μt(x1?x2)andμt(x2)≤ μt(x1?x2).So we getSimilarly,we can provethen we have||xj||Φ≤ ||x||Φ< γ ,j=1,2,3,4.Therefore there existsej∈P(M)such that Thus,the assertion holds. 48. Kind heaven help us now!: Gretel prays for heavenly assistance. Once again, these religious references were added by the Grimms.Return to place in story. Assume now that the family{an}is always given by(2). Proposition 1IfqΦ< ∞.Then the family{an}is b.u.e.m.at 0 on(LΦ(M),||·||Φ). ProofIt now follows from Lemma 1,that it is sufficient to show that{an}is b.u.e.m.at 0 onsince S+is dense inby Theorem 3.1 of[3]we only show that{an}b.u.e.m.at 0 on(S+,||·||Φ). So,let us fix ε >0 and δ >0.There exists such aand γ >0 be such thatwherecγis satisfied the inequality Takex∈S+such thatWe have whereHencefor alln. andThen we have Hence the required result follows. Theorem 1IfqΦ<∞.Then for eachx∈LΦ(M),the averages(2)converge b.a.u.to some ProofBy Proposition 1,we know that{an}is b.u.e.m.at 0 on(LΦ(M),||·||Φ).On the other hand,by Theorem 4.2 of[3],for eachx∈S,the averages(2)converge b.a.u.to someApplying Theorem 2.1 of[3],we know that for eachx∈LΦ(M),the averages(2)converge b.a.u.to somethen it follows immediately that{an(x)}converge toin measure.Next,we shall verify that Letx∈S andthen by(1),we can prove thatApplying Lemma 3.4 of[8],Lemma 4.1 of[9]and Fatou Lemma,we obtain which completes the proof. Let Φ(t)is N-function,defineGenerally Φ(2)(t)is not N-function.If Φ(2)(t)is N-function,thenin the same way Proposition 2Let Φ(t)andbe N-functions andqΦ<∞.Then the family{an}is u.e.m.at 0 on(LΦ(M),||·||Φ). ProofBy Lemma 1 and Theorem 3.2 of[3],it is enough to show that{an}is u.e.m.at 0 on Fixε>0 andδ>0.Since,due to Proposition 1,{an}is b.u.e.m.at 0 onthere exists such athatfor some If one takesthen fromit follows thatHenceTherefore,there issuch thatτ(e⊥)≤εandAplying Kadison’s inequality,we arrive at Thereforeand the assertion holds. 定理2If 2 ProofSinceSis dense inLΦ(M)and by Corollary 4.1 of[3]the sequencean(x)converges a.u.for allx∈S,applying Proposition 2 and Theorem 2.1 of[3],we infer that the averagesanconverge a.u.for allx∈LΦ(M),the fact that the corresponding limitsbelong toLΦ(M)follows as in Theorem 1.1 Preliminaries

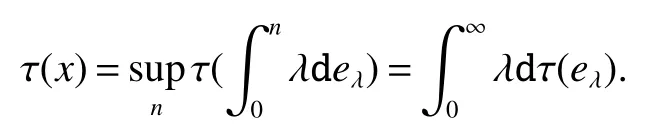

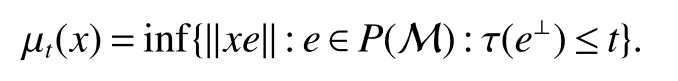




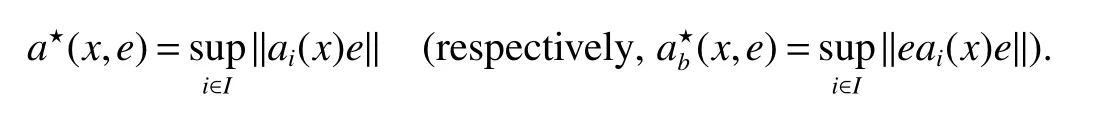


2 Individual ergodic theorems for noncommutative Orlicz space