函數(shù)不等式的幾種放縮法
2023-12-08 10:47:26陳彥男何紅梅
數(shù)理化解題研究 2023年31期
肖 剛 陳彥男 何紅梅 馬 杰
(1.宜賓學(xué)院理學(xué)部,四川 宜賓 644000;2.宜賓三中,四川 宜賓 644000;3.簡陽中學(xué),四川 宜賓 641499)
文章通過將數(shù)列不等式視為函數(shù)不等式,通過構(gòu)造法、聯(lián)想法等方法來證明不等式的成立.
1 巧用Sn構(gòu)造放縮函數(shù)
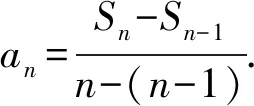
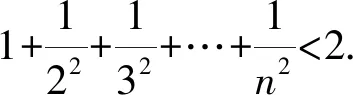
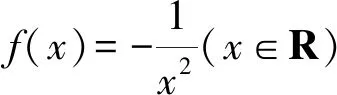
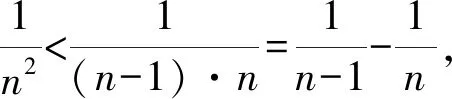
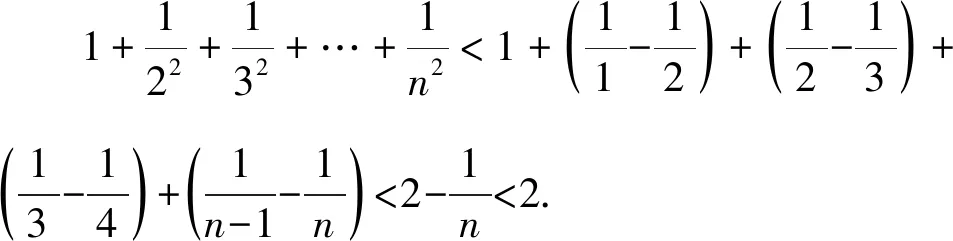
通過上述方法,我們很容易處理在自主招生和強(qiáng)基計(jì)劃中出現(xiàn)過的類似數(shù)列不等式問題,例如復(fù)旦自主招生試題和上海交大自主招生試題.
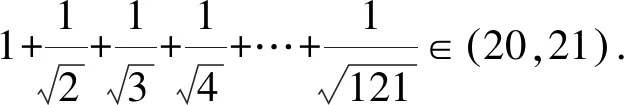
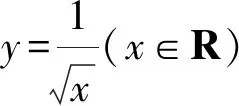
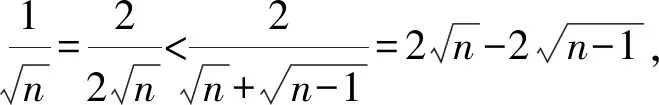
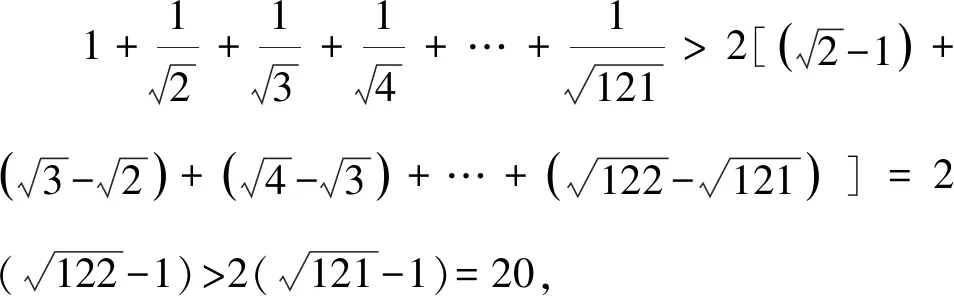

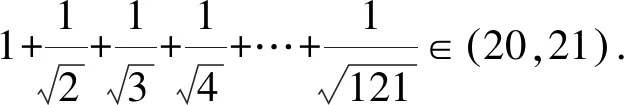
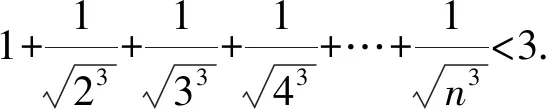
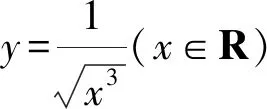
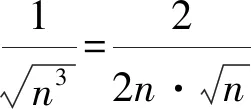
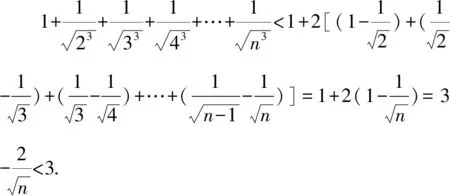
2 善用聯(lián)想法構(gòu)造新數(shù)列
對于常見的數(shù)列不等式,通常證明其小于或大于一個常數(shù).此時,可以將常數(shù)聯(lián)想成常見的數(shù)列[2].將數(shù)列不等式的證明轉(zhuǎn)換成兩個通項(xiàng)式的證明.例如卓越聯(lián)盟自主招生考試的壓軸題.
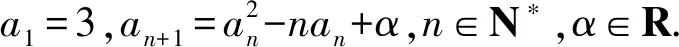
(1)若對?n∈N+,an≥2n成立,求α的取值范圍.
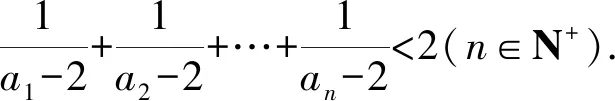
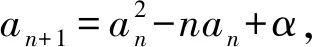
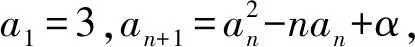
即需要證明:(1)an-2>(n-1)·n或(2)an-2>2n-1,對于(1)式,通過代入特例a1=3,a2=4,a3=6,a4=16,…,很容易否定(1)式不成立.而(2)式代入特殊項(xiàng)均成立.因此,需要證明an-2>2n-1,此式用數(shù)學(xué)歸納法即可證明.此題只給出第(2)問的詳細(xì)解答過程.
證明(2)當(dāng)n=1時,a1-2≥21-1,即a1≥20+2成立;
假設(shè)當(dāng)n=k時,ak-2≥2k-1,即ak≥2k-1+2成立;
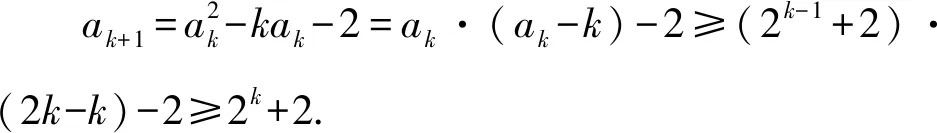
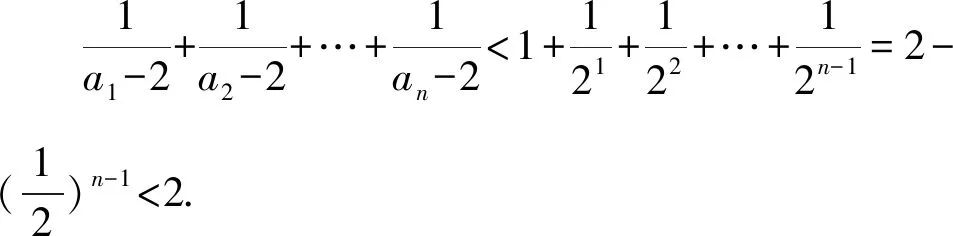
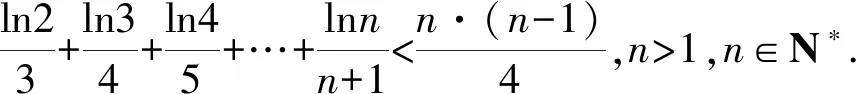
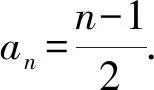
猜你喜歡
數(shù)學(xué)年刊A輯(中文版)(2021年1期)2021-06-09 09:32:06
文藝生活·中旬刊(2020年12期)2020-04-08 02:44:57
四川省干部函授學(xué)院學(xué)報(bào)(2019年1期)2019-06-25 00:53:36
成功(2018年11期)2018-12-28 09:18:54
新教育時代·教師版(2017年31期)2017-07-25 21:43:41
岷峨詩稿(2017年4期)2017-04-20 06:26:33
中國調(diào)味品(2017年2期)2017-03-20 16:18:19
山西大同大學(xué)學(xué)報(bào)(自然科學(xué)版)(2016年4期)2016-11-27 02:20:55
新高考·高一物理(2016年3期)2016-05-18 16:16:56
人民周刊(2016年4期)2016-02-29 15:53:30

