Dynamics of bubble-shaped Bose–Einstein condensates on two-dimensional cross-section in micro-gravity environment
Tie-Fu Zhang(張鐵夫), Cheng-Xi Li(李成蹊), and Wu-Ming Liu(劉伍明),3,?
1Beijing National Laboratory for Condensed Matter Physics,Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China
2School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China
3Songshan Lake Materials Laboratory,Dongguan 523808,China
Keywords: boson systems,ultracold gases,dynamic properties of condensates
1.Introduction
The bubble-shaped Bose–Einstein condensates with a topological structure,that is almost unattainable through conventional experiments on the Earth’s surface,[1]have been experimentally observed[2]in NASA Cold Atom Laboratory,[3]which provides the micro-gravity environment on the International Space Station.The seminal proposal of the matter–wave condensate bubbles was proposed by Zobay and Garraway,[4–6]and experimentally examined by several research groups.[7–10]The quantum bubble’s zero-temperature density distribution and free expansion have been studied[11]by the simulation of Gross–Pitaevskii equation,[12–15]which provides important references for the study of the bubbleshaped Bose–Einstein condensates in micro-gravity environments.
Recently, a series of advances have been made in the study of Bose–Einstein condensates in micro-gravity environments.[2,3,11,16–19]The mean-field theory developed by Bogoliubov provided an effective method for studying dilute Bose gas with weak repulsive interaction.[15,20]Subsequently,the Gross–Pitaevskii equation,which is based on this theory, has become the fundamental paradigm for investigating Bose–Einstein condensates and their matter–wave interference phenomena.[21–24]Through the numerically solving of the Gross–Pitaevskii equation,interesting phenomena such as variations in the thickness of bubble-shaped Bose–Einstein condensates and changes in interference fringes between two bubble-shaped Bose–Einstein condensates can be studied.The physical nature of bubble-shaped Bose–Einstein condensates still deserves attention.
In the presented study, the dynamical evolution of the bubble-shaped Bose–Einstein condensate has been investigated by numerically solving the Gross–Pitaevskii equation.In order to more effectively illustrate the variations in the density distribution of the condensate, we have selected a twodimensional(2D)cross-section of the three-dimensional(3D)bubble-shaped Bose–Einstein condensate as the focus of our study.Utilizing numerical solutions of the Gross–Pitaevskii equation, we generated the temporal density evolution plots for a singular bubble-shaped Bose–Einstein condensate, subsequently delving into the impact of the atomic interaction strength and the initial momentum on the density distribution.Employing the same methodology,we further examined the interference effects between the two bubble-shaped Bose–Einstein condensates.
2.Method: Gross–Pitaevskii equation
Consider the bubble-shaped Bose–Einstein condensate in micro-gravity environment where the gravitational force from the Earth is sufficiently weak to be negligible, under the description of the mean-field theory,[15,20]the time-evolution of the wave function can be described by the following Gross–Pitaevskii equation:[12–15]
whereφis the dimensionless wave function,τis the dimensionless time,and
is the Laplace operator of the dimensionless space coordinates characterized byξ,and the expression
is a dimensionless parameter, which characterizes the atomic interaction strength.The original variables (t,x, andψ) are presented by the dimensionless variables(τ,ξ,andφ)as follows:
whereαis the time unit,βis the space unit,andγis the wave function unit.Andt,x,ψare the original time, space, wave function variables of the original free Gross–Pitaevskii equation
where ˉhis the reduced Planck’s constant,Mandasare mass and s-wave scattering length of the atom,
is the Laplace operator.Under the condition for simplification:
this equation can be simplified into a dimensionless form in Eq.(1),which is convenient for calculation.
Regarding the bubble structure of the Bose–Einstein condensate,consider the 2D cross-section of the 3D bubble in order to simplify the calculations and emphasize the key physical issues.In this case, the 2D cross-section of a 3D bubble can be treated as a ring.The related schematic diagram has been presented in Fig.1.

Fig.1.The schematic diagram of a bubble-shaped Bose–Einstein condensate.(a) The contour of a bubble-shaped Bose–Einstein condensate in three-dimensional(3D)space.(b)The related 2D cross-sectional of the 3D bubble-shaped Bose–Einstein condensate.
Based on the density profiles of the bubble-shaped Bose–Einstein condensates in Refs.[1,2,25], and the longestablished tradition of postulating Gaussian wave packets as the initial wave functions of the Bose–Einstein condensates,[24,26,27]it is natural to assume that the condensate’s initial ground-state wave function satisfies the ringshaped Gaussian distribution
where|φdis|2satisfies the normalization condition
wherepiniis the initial momentum andβis the space unit.This momentum is related to the kinetic energy,which is characterized by the zero-point motion.[28]Let the macroscopic wave function be the product of the distribution function and the single particle wave function,the initial wave function can be presented as
where|φini|2also satisfies the normalization condition as given before
The dynamic evolution of the wave function of the ring-shaped Bose–Einstein condensate as the 2D cross-section of the 3D bubble can be characterized by numerically solving the dimensionless Gross–Pitaevskii equation(Eq.(1))with the initial condition(Eq.(6)).
3.Dynamics of individual bubble-shaped Bose–Einstein condensate undergoing free diffusion
Consider free diffusion of the bubble-shaped Bose–Einstein condensate in micro-gravity.To observe the timeevolution of the wave function of the 2D cross-section of a 3D bubble, the Gross–Pitaevskii equation in Eq.(1)was numerically solved with the initial condition in Eq.(6).
The time-evolution of the density distribution of the wave function for a bubble’s 2D cross-section is presented in Fig.2.This bubble is constructed by Bose–Einstein condensate with weakly repulsive interaction.It shows that, as the time increases,the outer surface of the bubble gradually spreads outward, and at the same time, the inner surface of the bubble also spreads inward.In other words,the bubble will gradually expand,while the thickness increases.
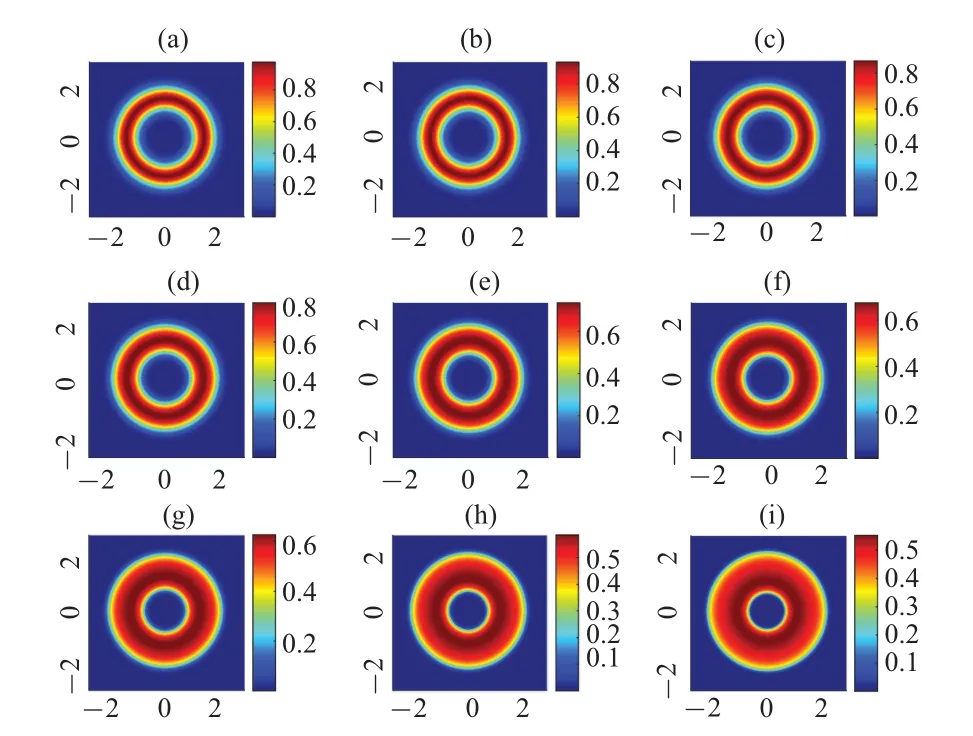
Fig.2.The time-evolution of the 2D cross-section of a 3D bubble-shaped Bose–Einstein condensate.Here,the parameters are set as η=3000,ρ0=2,σ =0.4,β pini/ˉh=1.The sub-figures present the distributions of|φ|2 from τ =0.001 in panel (a) to τ =0.009 in panel (i), the time interval between the neighbor sub-figures is 0.001.
The dynamics of the bubble may be influenced by the parameters in Gross–Pitaevskii equation and initial state.In order to explore the influences of the parameters,one of the parameters can be adjusted individually.First we adjust the interaction parameterηand numerically solve the Gross–Pitaevskii equation with corresponding different cases to observe the influences of the time-evolution of the wave function.
A comparison of the cross-section density distribution of the bubble-shaped Bose–Einstein condensates with different interaction parameterηis presented in Fig.3.From these results, it seems that the bigger interaction parameter may cause the faster evolution of the wave function, and in this case, the faster diffusion of the atoms of this bubble-shaped Bose–Einstein condensate.When the interaction parameter is sufficiently large and the time is long enough, the outer surface of the bubble will gradually expand and the density of the condensed matter in close proximity to the external surface will decrease.At the same time,the inner surface of the bubble will gradually contract inward, and the density of the condensed matter in close proximity to the inner surface will increase significantly.
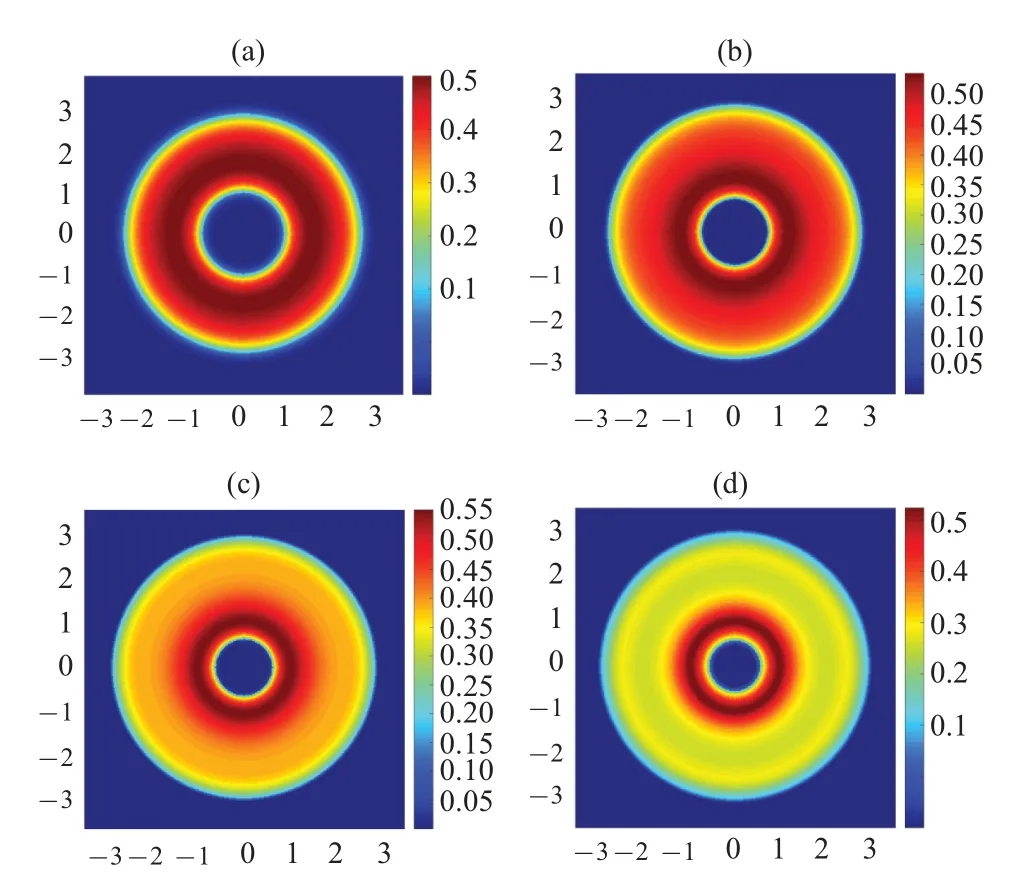
Fig.3.A comparison of the time-evolutions of the 2D cross-section of a 3D bubble-shaped Bose–Einstein condensate with different interaction parameters.Here,the common parameters are set as ρ0=2,σ =0.4,β pini/ˉh=1.The interaction parameters are set as η =2000 in panel (a), η =4000 in panel(b),η =6000 in panel(c),and η =8000 in panel(d).The time variable τ is fixed at τ =0.009.
In order to discover the deeper physical mechanisms behind this,the effects of the varying of other parameters should be considered.The initial momentum of the condensate is related to the kinetic energy which can be determined by the zero-point motion.[28]Choose different initial momentum parameters and solve the Gross–Pitaevskii equation, the results can be shown in the following figures.
In Fig.4, comparisons of the bubble’s density distribution in a 2D cross-section are shown at a specific time.In contrast to the findings presented in Fig.3,it is observed that augmenting the initial momentum parameter does not result in bubble thickening.Conversely,it is possible to observe bubble thinning when the initial momentum parameter is sufficiently large.This appears to be a counterintuitive result,and its physical essence necessitates further experimental and theoretical exploration to unveil.
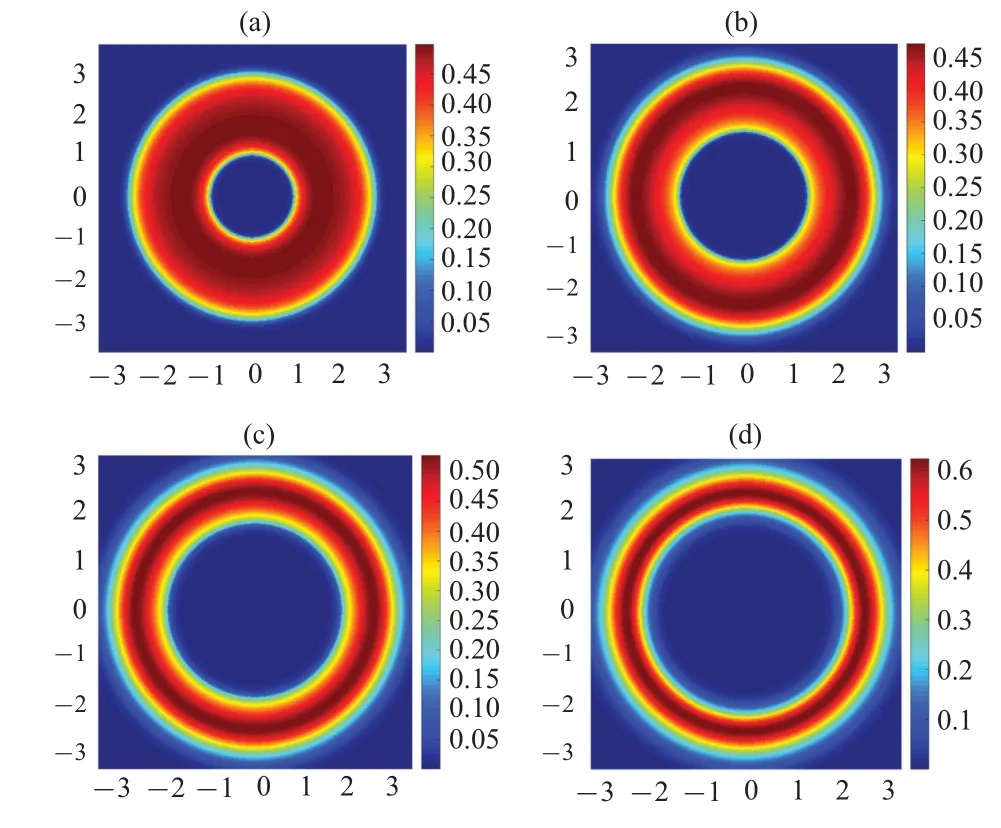
Fig.4.A comparison of the time-evolutions of the 2D cross-section of a 3D bubble-shaped Bose–Einstein condensate with different initial momentum parameters.Here, the common parameters are set as ρ0 =2, σ =0.4,η = 3000.The initial momentum parameters are set as β pini/ˉh = 10 in panel (a), β pini/ˉh = 40 in panel (b), β pini/ˉh = 70 in panel (c), and β pini/ˉh=100 in panel(d).The time variable τ is fixed at τ =0.009.
4.Interference between two bubble-shaped Bose–Einstein condensates and the associated dynamic evolution
To investigate the matter–wave interference of the bubbleshaped Bose–Einstein condensates in micro-gravity, consider two of them which have been separated by a distance in space.The initial wave function can be revised into
where
characterize the distance from the atoms in the left or right bubble condensate to the left or right center.Numerically solve Gross–Pitaevskii equation with this initial wave function of two bubble-shaped Bose–Einstein condensates in a 2D crosssection,the dynamical evolution of the distribution of the wave function can be drawn based on numerical results.
The time-evolution of two bubbles constructed by Bose–Einstein condensates in a 2D cross-section has been shown in Fig.5.As their wave functions begin to overlap,interference patterns emerge between the wave functions.With the passage of time,the overlapping region of the wave functions gradually increases,resulting in an increase in the number and density of interference patterns.

Fig.5.The time-evolution of the interference between two bubble-shaped Bose–Einstein condensates in a 2D cross-section.Here,the parameters are set as η =1500, ρ0 =1.5, σ =0.4, β pini/ˉh=5.The sub-figures present the distribution of|φ|2 from τ=0.001 in panel(a)to τ=0.009 in panel(i),the time interval between the neighbor sub-figures is 0.001.
The time-evolution of the wave function may be influenced by the value of interaction parameter,to investigate the related effects,the Gross–Pitaevskii equation should be solved with the initial wave function characterized by different interaction parameters.
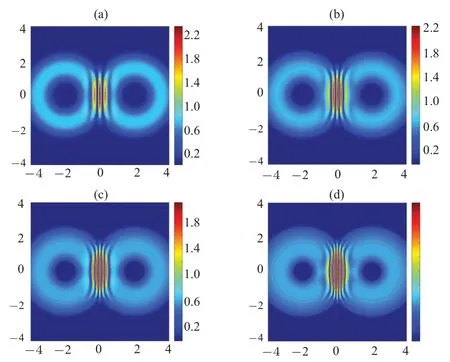
Fig.6.The comparison of the time-evolutions of the interference between two bubble-shaped Bose–Einstein condensates in cases with different interaction parameters.Here, the common parameters are set as ρ0 =1.5,σ =0.4, β pini/ˉh=5.The interaction parameters are set as η =500 in panel (a), η = 1000 in panel (b), η = 1500 in panel (c), η = 2000 in panel(d).The time variable τ is fixed at τ =0.009.
In Fig.6, the comparison of interference fringes of two bubbles constructed by Bose–Einstein condensates under different interaction parameters has been illustrated in a 2D cross-section.It can be observed that as the interaction parameter increases, the wave function of the bubbles expand more rapidly.This results in an increase in the number of interference fringes between the two bubbles, as well as an increase in the density of the interference fringes.
The initial momentum of the bubble is equally important to the time-evolution of the wave function.Similarly,exploring its effects can be achieved by selecting different initial momentum parameters to solve the Gross–Pitaevskii equation and generate wave function distribution plots.
The contrast of interference fringes between two bubbles constructed by Bose–Einstein condensates,depicted in Fig.7,has been shown based on the numerical solution of the Gross–Pitaevskii equation with different initial momentum parameters.It can be observed that, in this 2D cross-section, as the initial momentum parameter increases,the number of interference fringes between the bubbles increases, and the width of the interference fringes becomes narrower.Referring to the images of interference fringes under varying interaction parameters in Fig.6, it can be observed that the increase in the initial momentum parameter and the increase in the interaction parameter have similar effects on the interference fringes.

Fig.7.The comparison of the time-evolutions of the interference between two bubble-shaped Bose–Einstein condensates in cases with different initial momentum parameters.Here,the common parameters are set as ρ0 =1.5,σ =0.4,η =1000.The initial momentum parameters are set as β pini/ˉh=5 in panel(a),β pini/=10 in panel(b),β pini/ˉh=15 in panel(c),β pini/ˉh=20 in panel(d).The time variable τ is fixed at τ =0.009.
5.Discussion
Through numerically solving the Gross–Pitaevskii equation with different initial conditions,the time-evolution of the density distribution of bubble-shaped Bose–Einstein condensates has been presented in the figures shown above.
Based on the above results,it can be observed that the increase of the atomic interaction strength can cause the faster time-evolution of the wave function.And in the case of the interference between two bubble-shaped Bose–Einstein condensates appears, the increase of the atomic interaction strength can cause the enhanced interference effect which characterized manifestly by the increased number of interference fringes and the increased fringe density.The interaction strength is related to the atomic s-wave scattering length,which can be modified by external magnetic field through the effects of the Fano–Feshbach resonance,[29–35]these results can be examined by further related experiments.
The initial momentum that is related to the zero-point motion[28]can also influence the time-evolution of the density distribution of the wave function.Increasing the initial momentum can enhance the rate of time-evolution of the wave function, which is consistent with our physical intuition, as a larger initial momentum implies that microscopic particles have higher initial velocities, leading to faster macroscopic wave function evolution.Furthermore, a larger initial momentum also implies a shorter de Broglie wavelength, corresponding to shorter period of interference fringes.[24,28]However,increasing the initial momentum can also result in a thinner bubble-shaped Bose–Einstein condensate, which appears counterintuitive and requires further theoretical and experimental exploration to verify.
6.Conclusion
The dynamical evolution of the bubble-shaped Bose–Einstein condensates has been investigated by numerically solving the Gross–Pitaevskii equation with several different initial conditions.We studied the effects of atomic interaction strength and initial momentum on the time evolution of single bubble and interference patterns between two bubbles by analyzing the evolution images based on numerical results.We have discovered several interesting physical phenomena,such as the fact that bubbles with larger initial momentum,i.e.,stronger the zero-point motion,exhibit a thinning of their thicknesses after a certain period of evolution.This counterintuitive result requires further investigation to verify.Our findings will contribute to exploring the physical nature of bubbleshaped Bose–Einstein condensates and provide a valuable reference for future relevant experiments in micro-gravity.
Acknowledgements
Project supported by the National Key Research and Development Program of China(Grant Nos.2021YFA1400900,2021YFA0718300,and 2021YFA1402100),the National Natural Science Foundation of China (Grant Nos.61835013,12174461, 12234012, and 12334012), and the Space Application System of China Manned Space Program.
- Chinese Physics B的其它文章
- Robustness of community networks against cascading failures with heterogeneous redistribution strategies
- Identifying multiple influential spreaders in complex networks based on spectral graph theory
- Self-similarity of complex networks under centrality-based node removal strategy
- Percolation transitions in edge-coupled interdependent networks with directed dependency links
- Important edge identification in complex networks based on local and global features
- Free running period affected by network structures of suprachiasmatic nucleus neurons exposed to constant light

