橢圓及其輔助圓的6個弦長命題
山東省泰安市寧陽縣第一中學(271400) 劉才華
我們知道, 連接橢圓上任意兩點的線段叫作橢圓的弦, 通過橢圓焦點的弦叫作橢圓的焦點弦, 通過橢圓中心的弦叫作橢圓的中心弦.
定義1過橢圓的焦點且與過焦點的軸垂直的弦叫作橢圓的通徑. 易得橢圓的通徑長為

圖1
定義2以橢圓的長軸為直徑的圓叫作橢圓的輔助圓.
對于橢圓及其輔助圓,通過研究,我們得到如下6 個與弦長相關(guān)的命題.
命題1如圖1,圓? 為橢圓Γ 的輔助圓,AB為過橢圓Γ右焦點F的焦點弦,CD為過F的圓? 的弦,且AB ⊥CD,則|AB|·|CD|2=8ab2.
證 明(1) 當AB為 橢 圓Γ 的 長 軸 時,|CD|=則|AB|·|CD|2= 2a×4b2=8ab2.
(2) 當AB為橢圓Γ 的通徑時,CD為橢圓的長軸, 由8ab2.
(3) 當AB不為橢圓Γ 的長軸且不為通徑時, 設(shè)A(x1,y1),B(x2,y2), 直線AB的方程為y=k(x-c), 將其與橢圓方程聯(lián)立并消去y得(k2a2+b2)x2-2k2a2cx+k2a2c2-a2b2=0,則由橢圓的焦半徑公式得
直線CD的方程為即x+ky-c= 0.圓心O到直線CD的距離為
則
綜上得|AB|·|CD|2=8ab2.
命題2如圖2,圓? 為橢圓Γ 的輔助圓,F為橢圓Γ 的右焦點,AB為橢圓Γ的中心弦,CD為過F的圓? 的弦, 且AB ⊥CD, 則|AB|·|CD|=4ab.
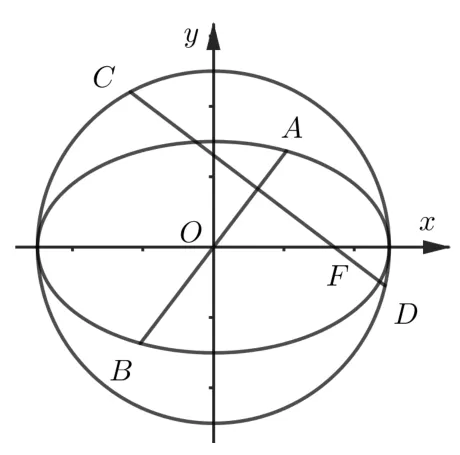
圖2
證明(1) 當AB為橢圓Γ 的長軸時,|CD|=由|AB|= 2a得|AB|.|CD|= 2a×2b=4ab.
(2) 當AB為橢圓Γ 的短軸時,CD為橢圓的長軸, 由|CD|=2a得|AB|.|CD|=2b×2a=4ab.
(3) 當AB不為橢圓Γ 的長軸和短軸時, 設(shè)A(x1,y1),B(x2,y2), 直線AB的方程為y=kx, 將其與橢圓方程聯(lián)立并消去y得(k2a2+b2)x2-a2b2= 0,則從而
直線CD的方程為即x+ky-c= 0.圓心O到直線CD的距離為則
綜上得|AB|.|CD|=4ab.
命題3如圖3, 圓?為橢圓Γ 的輔助圓,AB為過橢圓Γ 右焦點F的焦點弦,過橢圓Γ 的右頂點P與直線AB平行的直線交橢圓Γ 于C, 交圓? 于Q, 則|AB|.|PQ|=2a|PC|.
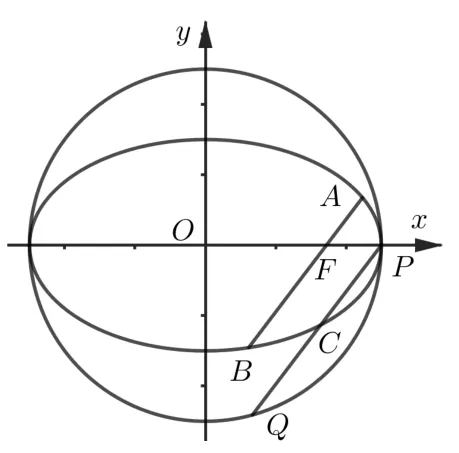
圖3
直線PQ的方程為y=k(x-a),圓心O到直線PQ的距離為故
所以|AB|.|PQ|=2a|PC|.
命題4如圖4, 圓?為橢圓Γ 的輔助圓,AB為過橢圓Γ 右焦點F的焦點 弦, 直 線AB交 圓? 于C,D, 則a2+b2.
證明(1) 當AB為橢圓Γ 的通徑時,由得
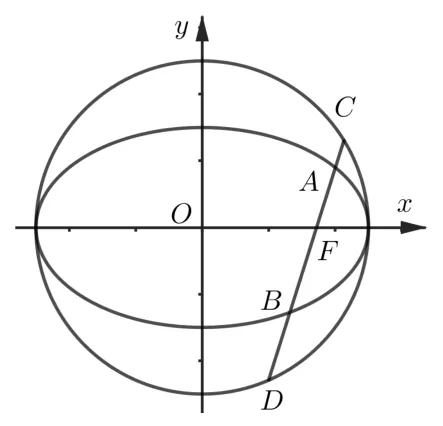
圖4
(2) 當AB不為橢圓Γ 的通徑時, 設(shè)直線AB的方程為y=k(x-c),A(x1,y1),B(x2,y2), 同命題1 的證明, 得|AB|=|AF|+|BF|=
直線CD的方程為y=k(x-c),即kx-y-kc= 0.圓心O到直線CD的距離為
則
命題5如圖5, 圓? 為橢圓Γ 的輔助圓,F為橢圓Γ 的右焦點,AB為橢圓Γ 的中心弦, 過F與直線AB平行的直線交圓? 于C,D, 則

圖5
證明(1) 當AB為橢圓Γ 的短軸時,由|AB|= 2b得
(2) 當AB不為橢圓Γ 的短軸時, 設(shè)直線AB的方程為y=kx,A(x1,y1),B(x2,y2), 由命題2 的證明得直線CD的方程為y=k(x - c),由命題4 的證明得則
命題6如圖6, 圓?為橢圓Γ 的輔助圓, 過?上任意一點P作橢圓Γ 的兩條切線, 切點為A,B, 直線AB分別交x軸,y軸于點M,N,O為坐標原點, 則
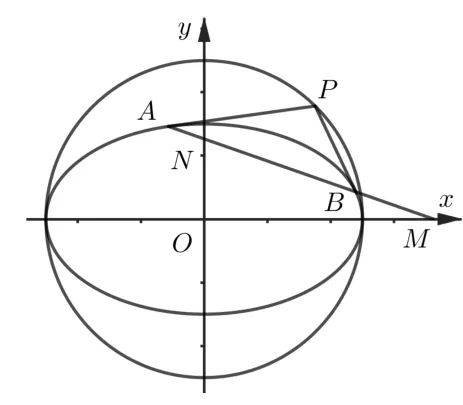
圖6
證明設(shè)P(acosθ,asinθ),θ ∈[0,2π),則直線AB的方程為得則
關(guān)于橢圓及其輔助圓應有許多優(yōu)美的性質(zhì),讀者可以進一步深入研究.

