圓錐曲線中非對(duì)稱韋達(dá)式的處理策略*
——一道考查數(shù)學(xué)運(yùn)算素養(yǎng)的高三試題分析

福建省泉州第一中學(xué) (362000) 張國(guó)川 任曉紅

解析幾何試題中,以斜率關(guān)系為考查背景的試題在各地模擬試題中經(jīng)常出現(xiàn),其本質(zhì)常與圓錐曲線的第三定義有關(guān),深層次的理論依據(jù)則是高等幾何中的極點(diǎn)極線問(wèn)題．利用代數(shù)方法解決幾何問(wèn)題的核心是將幾何基本量代數(shù)化,如將斜率用兩點(diǎn)坐標(biāo)表示,再根據(jù)題目將所要求解的斜率表達(dá)式整合成對(duì)稱韋達(dá)式,并將韋達(dá)定理整體代入求解即可．然而在一些模擬試題中卻出現(xiàn)了一些非對(duì)稱韋達(dá)式,比較簡(jiǎn)單的通常是將韋達(dá)定理中的兩個(gè)式子相除,得到兩根和與積的倍數(shù)關(guān)系,代入化簡(jiǎn)即可.可是有些試題如是操作卻不可行,本文結(jié)合一道高三試題的運(yùn)算處理談?wù)劮菍?duì)稱韋達(dá)式的處理策略,以此拋磚引玉.

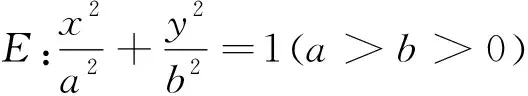
本題的難點(diǎn)在于如何處理非對(duì)稱式5x1+2x2=2,化歸成同系數(shù)韋達(dá)定理才能整體代入,實(shí)現(xiàn)運(yùn)算簡(jiǎn)化的目的．下面給出四種常見的非對(duì)稱韋達(dá)式的運(yùn)算處理策略:

策略1同系數(shù)配湊法

策略2方程求根法

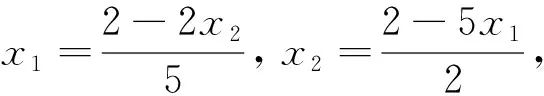
策略3待定系數(shù)法

由策略1的③式,知-9x1x2=[5(x1+x2)-2][2(x1+x2)-2](*)

策略4倒數(shù)構(gòu)造法

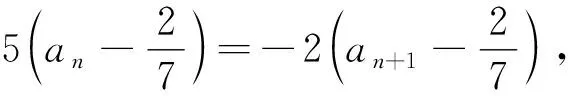
結(jié)語(yǔ)非對(duì)稱韋達(dá)式是圓錐曲線中一類比較特殊的代數(shù)結(jié)構(gòu),對(duì)學(xué)生處理代數(shù)式子的要求比較高,本質(zhì)上是考查學(xué)生如何將非對(duì)稱式子轉(zhuǎn)化成為稱式子,和數(shù)列中將非特殊數(shù)列化成特殊的等差或等比數(shù)列有異曲同工之妙,命題者的意圖旨在通過(guò)試題考查學(xué)生數(shù)學(xué)運(yùn)算的核心素養(yǎng),有利于培養(yǎng)學(xué)生熟練的式子變形能力,符合解析幾何考查代數(shù)運(yùn)算求解能力的基本要求．