Stable striped state in a rotating twodimensional spin–orbit coupled spin-1/2 Bose–Einstein condensate

Xuan Xu, Chao Gao, Ji Lin and Hui-jun Li

Institute of Nonlinear Physics and Department of Physics, Zhejiang Normal University, Jinhua 321004,China

Abstract We consider an effective two-dimensional Bose–Einstein condensate with some spin–orbit coupling(SOC)and a rotation term in an external harmonic potential.We find the striped state,and analyze the effects of SOC, the external potential, and the rotation frequency/direction on the profile and the stability of the striped state.Without the rotation term, the two spinor components exhibit striped pattern,and the numbers of stripes in the two components are always an odd–even or an even–odd.With the increase of the SOC strength, the number of stripes in both components increases, while the difference of the striped numbers is always one.After adding the rotation term, the profiles of the spinor components change qualitatively, and the change regulation of the striped numbers differs, while the difference of the striped numbers is still one.In addition, we find that the rotation direction only makes the striped state of the two spinor components exchange each other, though the clockwise and counterclockwise rotation directions are inequivalent with the presence of SOC.Such regulation is different from the previous study.And the rotation frequency gives rise to the transition from the striped state to a mixture of the striped state and vortex state.Furthermore,we prove the stability of these states by the evolution and linear stability analysis.

Keywords: spin–orbit coupling, Bose–Einstein condensate, the striped state

1.Introduction

The spin–orbit coupling(SOC)for electrons gives rise to diverse phenomena, including the splitting of fine structure in atomic physics, and multiple novel materials in condensed matter physics such as topological insulators,quantum anomalous Hall insulators and topological superconductors [1, 2].In contrast,there is no SOC effect for neutral atoms in their original state.

Since the synthetic SOC has been engineered in Bose–Einstein condensates (BEC), it provides us a highly controllable platform to study exotic quantum phenomena and novel states of matter[3–6],such as the plane-wave phase[7],the stripe phase [8–10], the lattice phase [11], skyrmion[12–14], the topological superfluid phase [5, 15–20], supersolid phase [6], soliton excitation [21–26], and half-quantum vortices[8,10,27].As a matter of fact,various SOC,such as the Rashba-type SOC[28],the Dresselhaus SOC[29],and the combination of Rashba and Dresselhaus SOC [30], can significantly affect the quantum states and dynamic properties of BEC, which result in rich physics.

On the other hand, rotation is one of the most common strategies to generate nontrivial states in BEC.The combined effect of SOC and rotation facilitates the states to exhibit various structures in spin-1/2[8],spin-1[31]and spin-2[32]BEC.However, certain carefully engineered SOC may offer opportunities to trigger even more novel excitation.

In the present work, we consider a special 2D SOC ∝σxkx+σxkycombined with rotation and a harmonic potential.Using the Newton conjugate gradient method[34],the mean-field Gross–Pitaevskii(GP)equation is solved,and a set of striped states is obtained.The effects of SOC intensity,potential intensity,and the rotation frequency and direction on the profiles and stability of the striped states are discussed.We find that the greater the SOC strength, the more the number of stripes.We also obtain that the weaker the strength of potential,the more the number of stripes and the rotation frequency will change seriously the profiles of striped states.In addition, we find the rotation direction only exchanges the striped states of two spinor components with each other, though the clockwise and counterclockwise rotation directions are inequivalent in this system.The stability of these striped states is also discussed by using numerical evolution and linear stability analysis.We find that the external potential favors the stability of the striped states,and the rotation frequency is unfavorable for stability.

The rest of the article is arranged as follows.Section 2 describes the model.Sections 3 and 4 discuss the striped states and their properties without and with the rotation term,respectively.In section 5,the effects of the harmonic potential and the rotation frequency on the profiles and stability of the striped states are discussed.The final section (section 6)contains a discussion and summary of the main results of our work.

2.SOC model with a rotation term

The dynamical behavior of BEC with the SOC and rotation term can be described by a normalized Gross–Pitaevskii equation:

Here(ψ1,ψ2)Tis the spinor macroscopic wave function,t is a dimensionless time coordinate, x, y are the dimensionless spatial coordinates,is the trapping potential with V0denoting the intensity of potential, βx,yrepresents the SOC strength, g1and g denote the intra- and inter-species interactions, the fifth term is the rotation term introduced by the z component of the angular-momentum operator, Ω ＞0 denotes the rotation frequency in the clockwise direction, the last term is the Rabi term.Inspired by the[33], the coefficients of the Rabi term and the rotation term are both denoted by Ω.

For discussing the stable solutions of equations (1) and their stability, nonlinear steady-state equations

are obtained by introducing the transformation ψj(x, y, t)=e?iμtφj(x, y), where μ is the chemical potential.By using the Newton conjugate gradient method [34], the profiles and power(which is proportional to the number of particles for the jth spinor component) of stable solutions are obtained in the following.Once the stable solutions φjare obtained, we can analyze their stability by adding the perturbations into them, i.e.

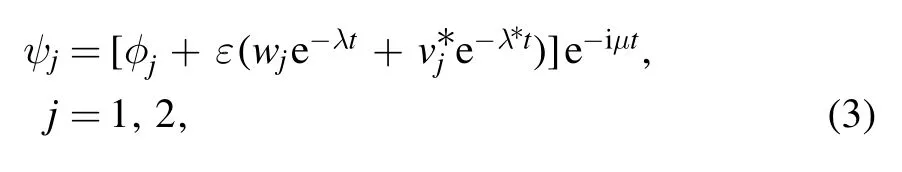
where wjand vjare the normal modes,and λ is the eigenvalue of the normal modes.Substituting equation (3) into equation (1), we get the following linear eigenvalue problem

after neglecting the higher order terms of O(εj) (j ≥2), with

L5=iβx?x+iβy?y,which can be solved numerically by using the Fourier collocation method [34].The solutions ψjare stable if the real parts of all the eigenvalues are non-positive.We also prove their stability through temporal evolution using the fourth-order Runge-Kutta method.In this paper, we only consider the repulsive interactions,such as,g1=1 and g=2,the homogeneous SOC in x and y direction, that is,βx=βy=β, and the chemical potential μ=0.6.

3.Striped states without rotation term

We now present the stable state solutions of equations (2)without the rotation, that is, Ω=0, and take V0=1.

The stable states with the striped patterns are shown in figure 1.Figure 1(a) shows the power curves which are the function of the SOC coefficient β.We can find the power increases gradually with the increase of SOC coefficient β, and the power curves of φ1and φ2almost coincide except for a small difference P1?P2as shown in the inset of figure 1(a).The stability of the solutions is checked by solving the eigenvalue problem (4).We check all the stable states corresponding to figure 1(a), and find all of them are stable.In figure 1(b), we choose three cases to show the results of stability,that is,β=1.2,2, 2.8.Their profiles with the striped pattern are shown in figures 1(c)–(e)for the component φ1,and figures 1(f)–(h)for the component φ2.We find that these two components have odd–even(or even–odd)stripe numbers in the case of taking the same β value.And,with increasing of β,the numbers of stripes for φ1,φ2are also increasing.

Figure 1.(a)Power curves of the striped states as a function of the SOC strength β.Here,the red solid line is for the component ψ1,and the blue dotted line is for the component ψ2.The difference between P1 and P2 is shown in the inset.(b) The eigenvalues of linear stability analysis for the corresponding striped states marked by the green dots in panel(a)are shown,β=1.2,2,2.8 respectively.(c)–(e)Profiles of the striped states for the components φ1 with different β=1.2, 2, 2.8.(f)–(h) Profiles of the striped states for the components φ2.The projections of the striped states are shown in the left and right insets.The left ones are for the initial value of evolution,the right ones are for the evolution results when t=100.

The stability of the solutions is also proved further by a numerical evolution of equations (1), with some random perturbations added into the initial values of evolution, i.e.the initial values are taken as ψ1,2(t=0,x,y)=φ1,2(x,y)(1+ερ1,2),where ε=0.01 and ρ1,2are the random variables uniformly distributed in the interval[0,1].In the insets of Figures 1(c)–(e)and(f)–(h),the left ones are the projections of spin components ψ1,2when t=0, and the right ones are the projections after evolution t=100.From these projections,we prove these striped states are stable.

The numbers of stripes for the spin components φ1,2are shown in figure 2.We can find the difference of the striped numbers for φ1,2is always 1.So, the numbers always keep an odd–even or an even–odd mode for the two spinor components.

Figure 2.The number n of stripes as a function of SOC strength β.The blue dashed line denotes φ1, and the green solid line indicates φ2.

4.Striped states with the rotation term

In this section,we will discuss the properties of striped states after adding the rotation term, that is, Ω ≠0.

After adding the rotation term, the properties of striped states are shown in figure 3.Here Ω=?0.25.Figure 3(a)shows the power curves which are the function of the SOC coefficient β.We find that the power still increases monotonically with increasing β.These eigenvalues which denote the stability of three striped states marked by green dots in figure 3(a) are shown in figure 3(b).Here,β=1,1.5,2.We also check all the eigenvalues of the striped states corresponding to every dot of the power curves and confirm that these striped states are all stable.Figures 3(c)–(e) and (f)–(h) display the typical profiles and their evolutions of these striped states with different β.Here β=1,1.5,2 respectively.In these insets,the left ones show the projections of the initial values,the right ones are the evolution results when t=100.Compared to the null background of striped states in figure 1, these striped states appear on a mountain-like background in figure 3.These evolution results prove further that they are stable.And the numbers of stripes still increase with increasing β.

Figure 3.(a)Power curves of the striped states as a function of the SOC strength β.Here,the red solid line is for the component ψ1,and the blue dotted line is for the component ψ2.The difference between P1 and P2 is shown in the inset.(b)The eigenvalues of linear stability analysis for the corresponding striped states marked by the green dots in panel(a)are shown,β=1,1.5,2 respectively.(c)–(e)Profiles of the striped states for the components φ1 with different β=1, 1.5, 2.(f)–(h) Profiles of the striped states for the components φ2.The projections of the striped states are shown in the left and right insets.The left ones are for the initial value of evolution, the right ones are for the evolution results when t=100.

In figure 4, the numbers of stripes for the spin components φ1,2are shown.We can find the difference between the striped numbers for φ1,2is still 1.So, the numbers always keep an odd–even or an even–odd mode for two spinor components with or without the rotation term.

Figure 4.The number n of stripes as a function of SOC strength β.The blue dashed line denotes φ1, and the green solid line indicates φ2.

We also discuss the effect of rotation direction on the striped states.From equations (1), it is obvious that the clockwise and counterclockwise rotation directions are inequivalent.In[33],the authors state that the properties of the stable states differ for the positive and negative rotation frequency.However,we find some counterintuitive results as shown in figure 5.Figures 5(a),(c)are the profiles of the striped states with Ω=0.25 and β=1.Figures 5(b), (d) are states of another type with the rotation frequency Ω=0.25 and β=0.5.These insets are the projections.The right ones are the projection of the profiles,and the left ones are the projection for the opposite rotation frequency.For the striped states, the rotation direction makes the two spinor components exchange each other,but for other states,the rotation direction does not affect their profiles.

Figure 5.Profiles and projections(right insets)of stable states for φ1 and φ2.(a),(c)The striped states with β=1 and Ω=0.25.(b),(d)The localized stable states with β=0.5 and Ω=0.25.In the left insets, the projections of stable states are shown with different rotational direction Ω=?0.25.

5.Striped states with different potential intensities and rotation frequencies

In this section, the effects of external potential and rotation frequency on the properties of the striped states are discussed.Here, we take β=1.

In figure 6,we study the effect of the intensity of external potential V0on the profiles of striped states without the rotation term,that is,Ω=0.The profiles and evolution results with different V0are shown in figures 6(a)–(c) and (d)–(f),respectively.We find that the numbers of stripes increase with decreasing V0.So, the external potential is very important to generate the striped states.

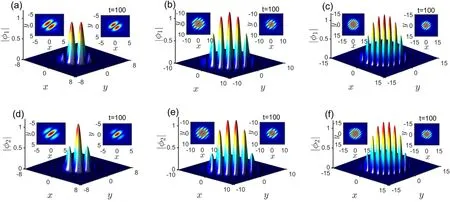
Figure 6.Profiles and evolutions (right insets) of the striped states with different V0.(a), (d) for V0=0.5.(b), (e) for V0=0.1.(c), (f) for V0=0.05.Here, Ω=0.The left insets are the projections of the initial profiles, and the right ones are the projections of evolution results when t=100.

In figure 7, we discuss the effect of the intensity of external potential V0on the profiles of striped states after considering the rotation term.In particular, Ω=?0.25.The profiles and evolution results with different V0are shown in figures 7(a)–(c) and (d)–(f).We find that these striped states are stable according to the evolution results of the right insets,and the numbers of stripes still increase with decreasing V0.However, the stripes become indistinguishable with decreasing V0.

Figure 7.Profiles and evolutions (right insets) of the striped states with different V0.(a), (d) for V0=0.7.(b), (e) for V0=0.5.(c), (f) for V0=0.3.Here,Ω=?0.25.The left insets are the projections of the initial profiles,and the right ones are the projections of evolution results when t=100.

For studying further the interplay of external potential and rotation frequency, we change the relative strength between the potential intensity and the rotation frequency.Figures 8(a)–(c) and (d)–(f) show correspondingly the profiles, the projections of initial profiles and phases, and the projections of the evolution results for V0=0.1, while figures 8(g)–(i) show the effects of the external potential V0and rotation frequency Ω on the stability.From these profiles,we find that the striped states become a combination of striped states and vortex states with increasing rotation frequency,and the number of vortexes is also increasing.From the stability analysis results, the stable region becomes narrow with increasing the rotation frequency Ω, the external potential favors the stability of the striped states, while the rotation frequency is unfavorable for the states’ stability.In the weaker external potential, the rotation will result in a transition from the stripe states to the mixed states of striped and vortex states.

Figure 8.Profiles and evolutions (right insets) of striped states with different Ω.(a), (d) for Ω=0.(b), (e) for Ω=?0.15.(c), (f) for Ω=?0.25.Here, V0=0.1.The left insets are the projections of the initial phases and profiles, and the right ones are the projections of evolution results when t=100.(g)–(i) Stability curves of stable states as a function of V0 with Ω=0, ?0.15, ?0.25, respectively.

6.Conclusion and summary

In conclusion,we have proposed a special two-dimensional SOC BEC model with a rotation term and a harmonic potential.The generation,stability,and controllability of the striped states were discussed by changing the SOC strength,the intensity of external potential,frequency,and direction of the rotation.These elements not only change the profiles of striped states but also affect their properties.After introducing the rotation term,the background of striped states changes from the null background to the mountainlike one.And with or without the rotation term, the numbers of stripes always kept the even–odd or odd–even mode for the two spinor components.We also find that the rotation direction only makes the striped states of the two spinor components exchange with each other,rather than causing other differences.Finally,we discuss the importance of the external potential and the competition between the external potential and the rotation frequency and find that the rotation might cause a transition from the striped states to the mixed states of striped and vortex states when the external potential is weak.

Acknowledgments

Project supported by the National Natural Science Foundation of China (12074343, 11835011, 12074342), Natural Science Foundation of Zhejiang Province of China (LZ22A050002,LY21A040004, LR22A040001).

ORCID iDs