基于迭代學(xué)習(xí)的具適多智能體系統(tǒng)分布式跟蹤控制
王小文 ,劉 帥 ,王錦榮
(1.山東大學(xué)控制科學(xué)與工程學(xué)院,山東濟(jì)南 250061;2.貴州大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,貴州貴陽(yáng) 550025)
1 Introduction
Multi-agent systems are composed of a set of intelligent agents that through mutual communication,cooperation,and other ways to complete complex tasks that a single agent cannot realize.Distributed cooperative control of multi-agent systems include consensus,flocking,formation,swarming and rendezvous has been concerned by many researchers due to its wide applications in many areas such as physics [1],biology [2],satellites[3]and control engineering[4].In particular,the consensus tracking control problem[5-7]is a kind of practical cooperation task that all agents are required to achieve specified value as desired.It can be applied in the vehicles and aerospace areas,exploration of unknown environments,navigation in harsh environments,cooperation on transportation tasks,helicopters and so on[8-10].
In recent years,researchers have proposed many approaches for the multi-agent system to realize desired consensus tracking from initial configuration [11-13].For example,Liu et al.[14]studied the leader-following exponential consensus tracking problem with abrupt and incipient actuator faults under edge-fixed and edgeswitching topologies.Cao and Song [15] developed a distributed adaptive control scheme to complete the consensus tracking problem for high-order multiagent systems with consensus error transformation techniques.
However,the above literatures can only guarantee the realization of the desired consensus tracking asymptotically or in finite time.In practice,considering the safety and effectiveness of operation,a group of agents have to keep relative position during the whole process when performing specific repetitive tasks,such as a group of autonomous vehicles[16]and UAVs[17]cooperative to deliver huge goods and patrol in the air,respectively.Iterative learning control(ILC)[18]is an accurate technology by correcting the deviation between the output signal and the desired target to improve the performance of the system,which is suitable for solving the above problems.Recently,there are many researches on multi-agent systems consensus tracking control with ILC technology.Xiong et al.[19]presented quantized iterative learning controllers for digital networks to achieve the consensus tracking in a finite time interval with limited information communication.For a class of nonlinear multi-agent systems,Bu et al.[20]proposed a distributed model free adaptive ILC control protocol to solve the consensus tracking problem.To achieve the high precision consensus tracking,Zhang et al.[21]gave a unified ILC algorithm for heterogeneous multivehicle systems with switching topology and external disturbances.
In 2014,Khalil et al.[22]introduced the new concept of conformable derivative which is a natural extension of the usual derivative.The conformable derivative is well-behaved and obeys the chain rule and Leibniz rule.A rich number of relevant theoretical results are emerging [23-25].It has attracted the attention of researchers due to its applications in various area,such as biology [26],physics [27],finance [28] and so on.Therefore,it is of great practical interest to study the distributed consensus tracking control for conformable multi-agent systems.
Motivated by the above discussion,the main purpose of this paper is to design appropriate protocols by using the ILC theory to achieve perfect tracking over finite time intervals.The main contributions of this paper can be summarized as follows:we considered a new simple well-behaved definition of derivative called conformable derivative in this paper.Different from the traditional difference method,conformable derivative can characterize a different step in real data sampling.The proposed distributed iterative learning-based scheme is a significant extension of the ILC approach to multiagent systems and brings new alternatives to solve distributed consensus problems over finite time intervals.
The remainder of the paper is arranged as follows.The consensus tracking problem is formulated in Section 2.In Section 3,we present a distributed iterative learning scheme.Main results of this paper are given in Section 4,where the convergence conditions are analyzed.In Section 5,two simulation examples are given to illustrate the results.Finally,the conclusions are drawn in Section 6.
for someλ>0 and 0<α<1,where‖.‖is any generic norm defined in the vector space Rn.N+stands for the set of positive integers.Given vectors or matricesAandB,A ?Bdenotes the Kronecker product ofAandB.
Preliminaries in graph theory: The communication topology of multi-agent systems composed ofNagents can be described by a graphG(V,E,A),whereV{1,2,...,N}is the set of vertices,E ?V ×Vis the set of edges,andAis the adjacency matrix.The set of neighboring nodes of theith agent is denoted byNi(j,i).If,thejth agent can receive the information from theith agent.A[ai,j]RN×Nis the adjacency matrix ofGandai,i >0.Setai,j >0 for(j,i)andai,j0 otherwise.LetL[li,j]RN×Ndenote the Laplacian matrix ofGwhereli,iandli,j-ai,jif.Define a directed path as a sequence of edges of the form(i1,i2),(i2,i3),...,(in-1,in).A directed graph is known as containing a spanning tree if the graph has at least one agent(as a root agent)with a directed path to any other agent.
2 Problem formulation
In this paper,we consider the iterative learningbased consensus tracking control for the following linear and nonlinear conformable multi-agent systems with repetitive properties as follows:
and
Moreover,we rewrite the system in a compact form.For thekth iteration in the multi-agent systems,(1)and(2)can be rewritten as
and
Definition 1[22,Definition 2.1] The conformable derivative with lower indexaof a functionx: [a,∞)→R is defined as
Obviously,each statexk(t)of(3)and(4)with the initial statexk(0) and control functionuk(t) have the form,respectively
and
Letyd(t) denote the desired trajectory for consensus tracking,which is regarded as a leader and index it by vertex 0 in the directed graph.Consequently,the united graph describing the information interaction between the leader and followers can be defined byG+(V ∪{0},E+,A+),whereE+is the edge set andA+is the adjacency matrix of graphG+.The communication topology of multi-agent systems is assumed to be described by graphG+,where each agent is corresponding to a node inG+.Meanwhile,we assume the virtual leader has at least one path to connect with any follower such that all the followers can receive the control objective from the leader.That is,the directed graphG+contains a spanning tree with the virtual leader being the root.The main objective of this paper is to design appropriate distributed iterative learning schemes to guarantee all the agents implement the desired consensus tracking control over a finite time interval.
3 Distributed iterative learning scheme
ILC is used to realize the complete tracking task in a finite time interval by repeating the control attempt of the same trajectory and correcting the unsatisfactory control signal with the tracking error between the output signal and the desired trajectory.We defined the tracking error as the difference between the real-time relative outputs and the desired trajectory.In this section,we shall design distributed iterative learning schemes to drive the above tracking errors to converge to zero so that the multi-agent systems can implement the desired consensus tracking control objective.
We denoteηk,j(t) as the available information at the(k+1)th iteration for thejth agent.Consider
wheresjequals 1 if thejth agent can access the desired trajectory and 0 otherwise.Letek,j(t)yd(t)-yk,j(t)be the tracking error.Further,we can get
Remark 1We shall design distribute protocols that only use the relative output instead of absolute measurements of output in the global framework.Each agent measures relative output errors through information interaction with neighbors in the local framework by limited communication.
For system(3)and(4),we consider the P-type and the PDα-type learning law with the initial state learning law,respectively
and
Remark 2Complete tracking can only be achieved under strict initial reset conditions,that is the initial state of the system is exactly equal to the expected initial state.However,it is difficult to meet the above conditions in actual situations.Therefore,we relax the initial value conditions and design the initial state learning laws.
Remark 3Initial state learning laws can be recognized as discrete-time consensus protocols.That is,the iteration-axis can be treated as a discrete time-axis.under the proposed learning laws,the initial states of all agents can converge to the desired value over a finite interval.
For thekth iteration,we denote the column stack vectors:ηk(t)[ηk,1(t)T...ηk,N(t)T]T,xk(t)[xk,1(t)T...xk,N(t)T]T,yk(t)[yk,1(t)T...yk,N(t)T]T,uk(t)[uk,1(t)T...uk,N(t)T]T,ek(t)[ek,1(t)T...ek,N(t)T]T.Therefore,linking (8) and both P-type and PDα-type learning law by using Kronecker product,we obtain
and
whereImandLdenotem×midentity matrix and graph Laplacian ofG,respectively,andSdiag{s1,...,sN},si≥0(i1,2,...,N).Then,the convergence of this distributed iterative learning scheme will be analyzed in the next section.
Remark 4In practical application,we can set to stop the iteration when the consensus tracking error is less than the actual required value.That is,we can stop the iteration if there exists ak ∈N+such that|ek(t)| <?,where?>0 is a preset parameter according to the actual demand.
4 Convergence analysis
In this section,we shall present two main results on the convergence of the proposed scheme.
4.1 Convergence analysis of P-type learning law for linear systems
First of all,we establish the following theorem by combining the P-type iterative learning law and multiagent consensus tracking control of linear comformable systems(3).
Theorem 1Consider the linear multi-agent systems(3)with P-type learning law(9).Suppose a directed graphG+contains a spanning tree corresponding to the communication topology.If control gains satisfy
and
then the consensus tracking errorek(t)→0 as iterationk →∞,i.e.yd(t)for all[0,T].
ProofAccording to(9),the tracking error of the(k+1)th iteration can be written as
which yields that
Then taking the matrix norm for the above equality,we have
By condition(11),one can obtain
Then using(9)to the states of all the agents(5),we get
Denotingδxk(t)xk+1(t)-xk(t),we have
Taking supremum,we get
where we denoteM‖IN ?A‖.
For(13),taking the matrix norm,we can have
Taking theλ.α-norm and substituting(17)into(18)for the above inequality yield
4.2 Convergence analysis of PDα-type ILC for nonlinear systems
Next,we will give the following theorem for the combined studies of PDα-type ILC law and multi-agent consensus tracking control of nonlinear conformable systems (4).It is necessary to give the following assumption.
A1) Globally Lipschitz condition: The time-varying nonlinear functionf(xz,t),satisfies
whereγ≥0 is constant.
Theorem 2Consider the nonlinear multi-agent systems(4)with PDα-type learning law(10).Suppose assumption A1) holds and directed graphG+contains a spanning tree corresponding to the communication topology.If control gains satisfy
then the consensus tracking errorek(t)→0 as iterationk →∞,i.e.yd(t)for all[0,T].
ProofThe tracking error of the(k+1)th iteration can be written as
Based on(10)and(21),one can obtain
Then,taking the matrix norm to both sides,it has
According to(20),we get
By the state equation (6) and PDα-type iterative learning law(10),we haveδxk(t)xk+1(0)-xk(0)+
Then,taking norm for the above inequality and implementing into A1),we can get
Note that (‖(L+S)?BWPD2‖+‖(L+S)?BWPD1‖tα)eλt‖ek‖λis a nondecreasing function on[0,T].Applying the Gronwall inequality for‖δxk(t)‖,we have
whereω(t)‖(L+S)?BWPD2‖+‖(L+S)?BWPD1‖tα.Moreover,takingλ-norm,one can obtain
By(21)and(23),it follows with
Taking norm for(25),we have
Substituting(27)into(26),we get
Next,takingλ-norm and substituting(24)into(28)
5 Simulation examples
Two simulation examples are performed to illustrate the effectiveness of the proposed distributed iterative learning protocols.
The interaction graph among agents is described by an directed graphG+(V ∪{0},E+,A+)in Fig.1,where vertex 0 represents the virtual leader.We adoptai,j1 if(i,j).It is easy to get the Laplacian matrix for followers
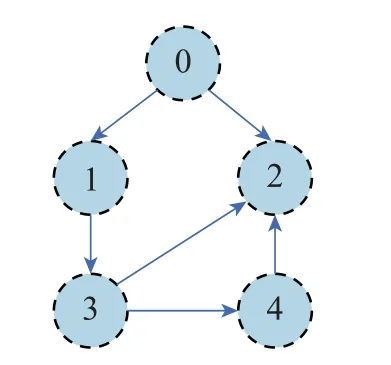
Fig.1 Directed communication topology among agents in the network
andSdiag{1,1,0,0},
In this section,we setα0.7.The norm of the tracking errors in each iteration is designated 2-norm in the following examples.The initial state at first iteration is chosen asx1[1-3]T,x2[2-1]T,x3[0 4]T,andx4[-1 2]T.The desired initial state is uniquexd0.The initial control signalu1,i0,i1,2,3,4 for all agents.
Example 1Consider the multi-agent system(3)as follows:
and the desired reference trajectory
To verify the contraction conditions in Theorem 1,we select the learning gain matrix
By explicit calculation,we can obtain that‖ImN -(L+S)?DWP‖0.9895<1 and‖ImN-(L+S)?CWP0-(L+S)?DWP‖0.9899<1.The convergence condition in Theorem 1 is satisfied so that the consensus tracking can be achieved.Fig.2 shows the initial state learning of agents.Fig.3 shows the output of a leader and four agents at the 1st and 100th iteration.Fig.4 depicts the tracking errors of each agent.It is easy to see all the initial states and outputs converge to the desired trajectory over a finite time interval,respectively.
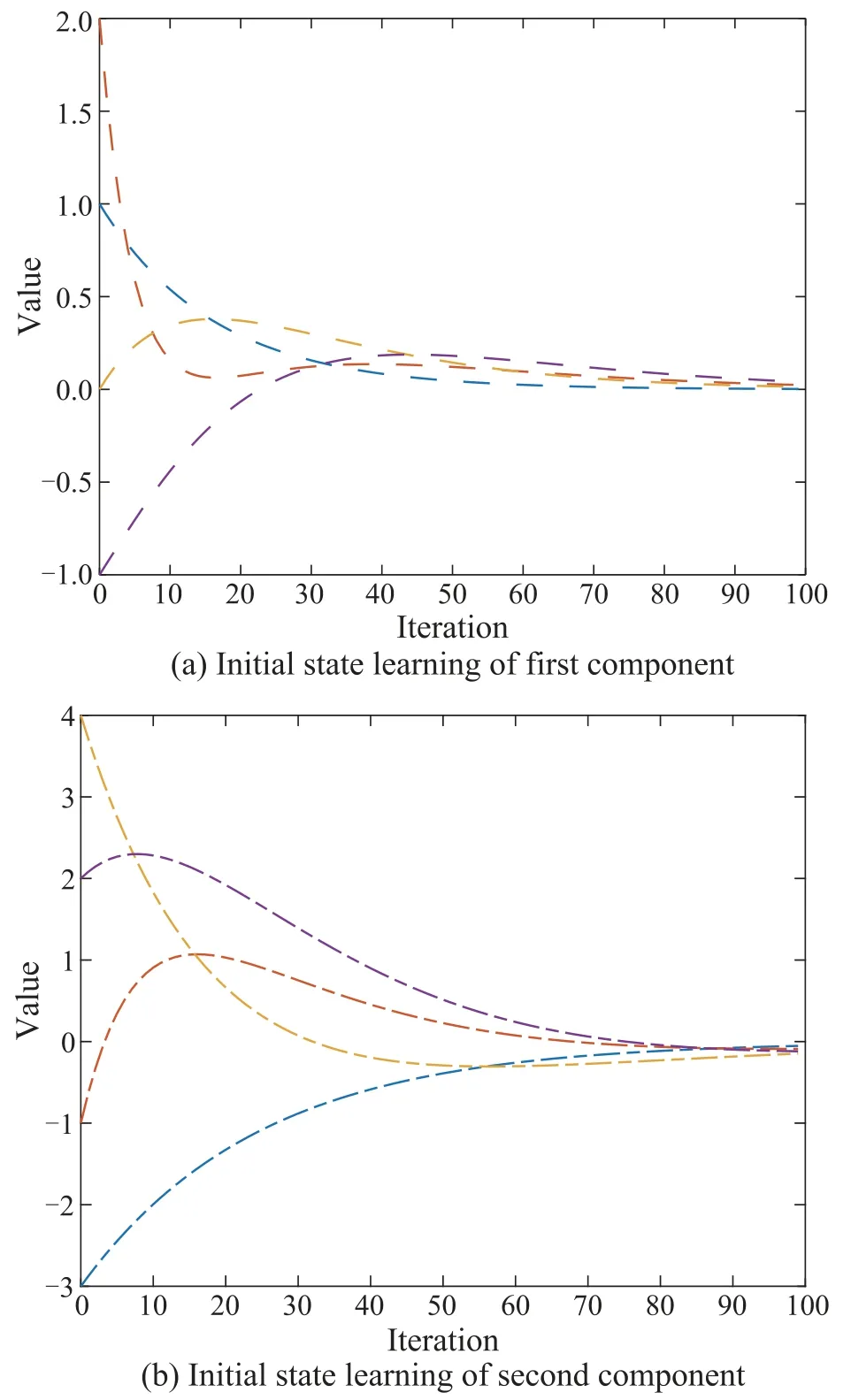
Fig.2 Initial state value at each iteration under P-type learning law
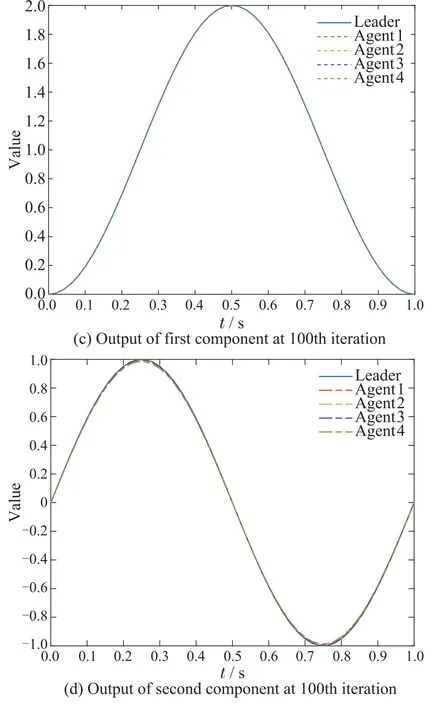
Fig.3 Output trajectory at 1st and 100th iteration under P-type learning law

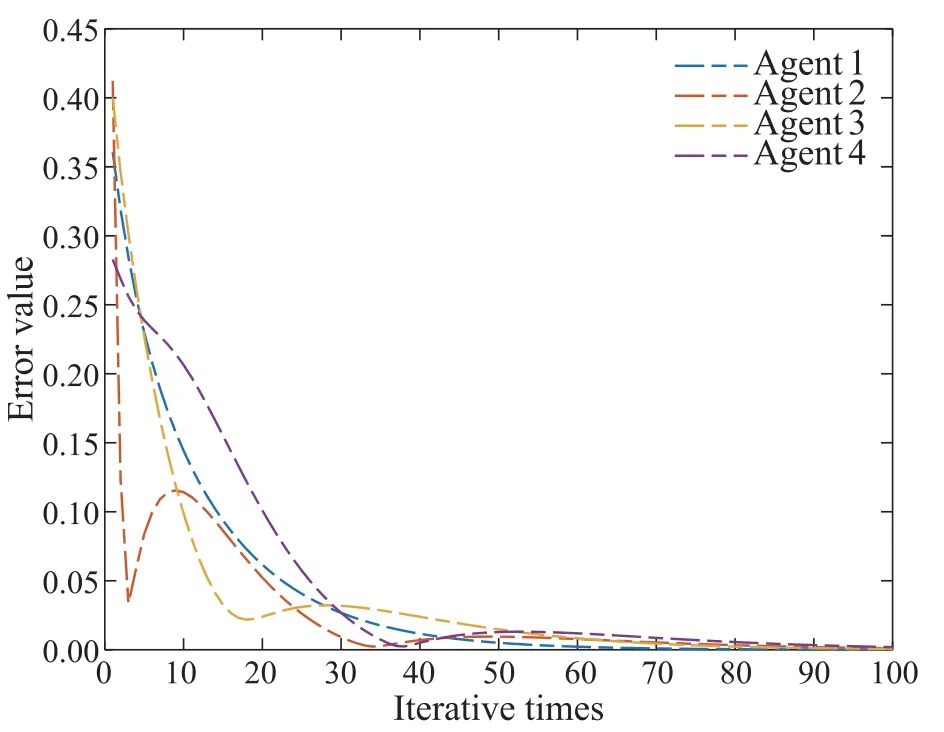
Fig.4 The tracking error at each iteration under P-type learning law
Example 2Setxk,i(t) :[xk,i,1(t)xk,i,2(t)]Tfor each agent.Consider the multi-agent system(4)as follows:
and the desired reference trajectory
To verify the contraction conditions in Theorem 2,we select the learning gain matrix
Through simple calculation,we can get‖ImN -(L+S)?CBWP2‖0.9318<1.The convergence condition in Theorem 2 is satisfied so that the consensus tracking can be achieved.Fig.5 shows the initial state learning of agents.Fig.6 shows the output of a leader and four agents at the 1st and 50th iteration.Fig.7 depicts the tracking errors of each agent.It is easy to see all the initial states and outputs converge to the desired trajectory in a finite time interval,respectively.
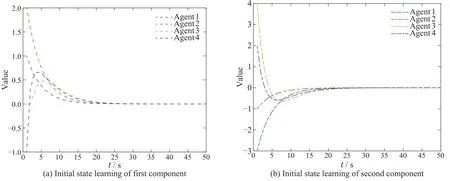
Fig.5 Initial state value at each iteration under PDα-type learning law
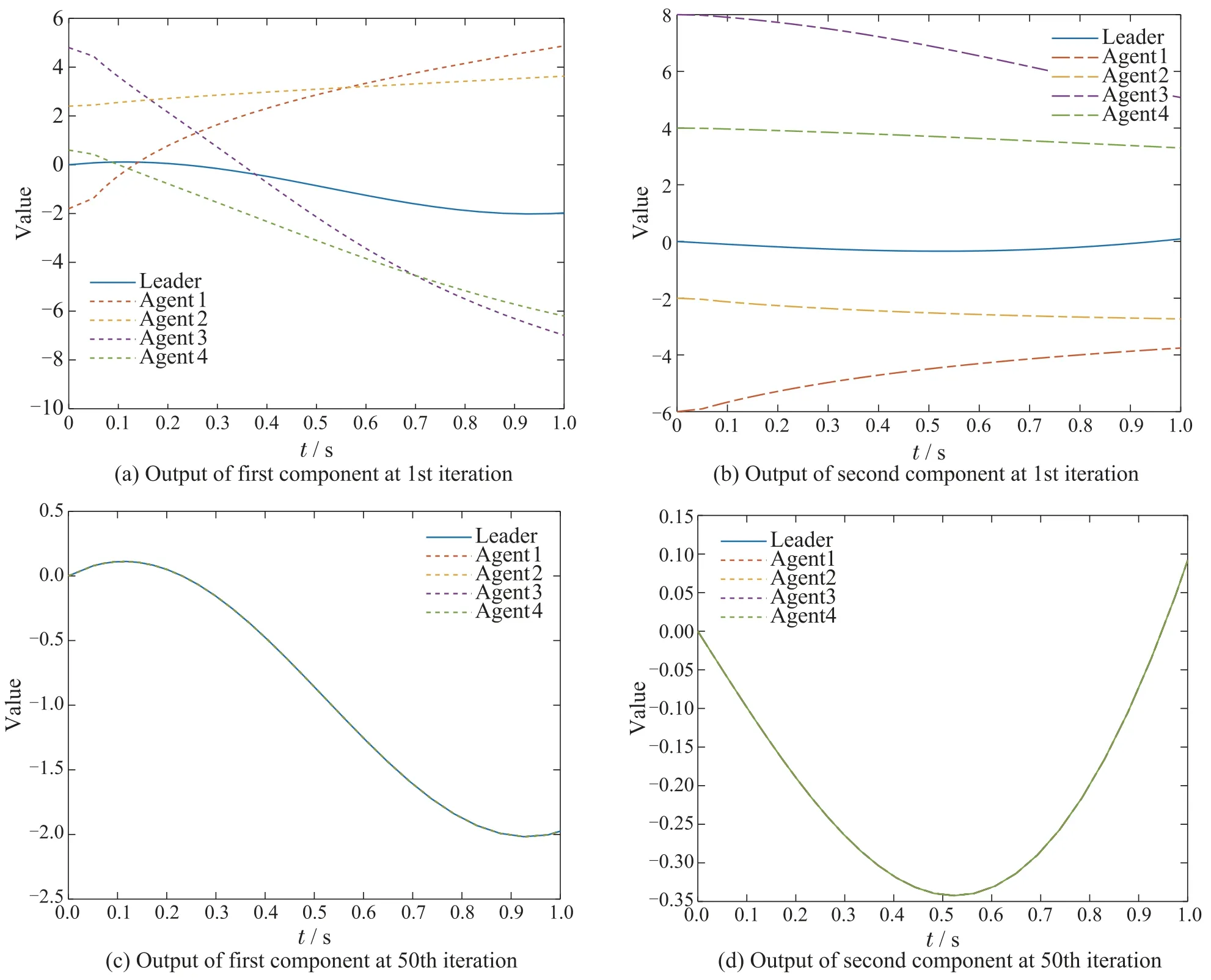
Fig.6 Output trajectory at 1st,10th,and 50th iteration under PDα-type learning law
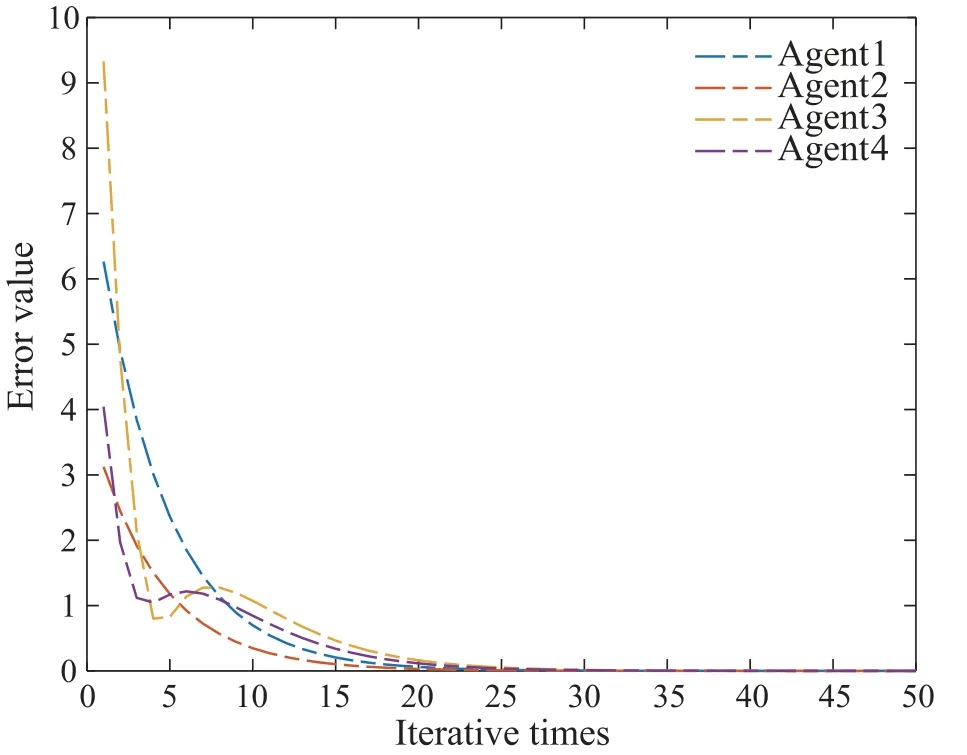
Fig.7 The tracking error at each iteration under PDα-type learning law
6 Conclusions
In this paper,the finite-time consensus tracking control problem for conformable multi-agent systems has been addressed.Under the proposed distributed iterative learning scheme,the desired consensus tracking can be achieved over a finite interval as the iteration increases.By using initial state learning laws,the performance of our protocol can be improved to reach the perfect tracking of the desired trajectory.Two simulations are given to verify the effectiveness of our results on iterative learning-based consensus tracking control.In our future work,the derived protocols will be further studied to provide them with explicit application validations by considering some practical applications such as biomedical science and intelligent unmanned systems.

