SOME RESULTS ON THE SIXTH-ORDER BOUNDARY VALUE PROBLEMS*
Wu Li
(Department of Mathematics and Physics,Nanjing Institute of Technology,Nanjing 211167)
Zhang Liyuan
(Department of mathematics,Nanjing university of Aeronautics and Astronautics,Nanjing 211106/Xingtai No.2 Middle School,Xingtai 054001)
Abstract In this paper,we establish some existence results of positive solutions of the nonlinear sixth-order periodic boundary value problem:
Keywords Six order differential equation,Positive solutions,Cone,Fixed point index theorem
1 Introduction
This paper is concerned with the existence of nontrivial solutions for the periodic boundary value problem

whereA,B,Care some given real constants andf(x,u)is a continuous function on R2.This problem is motivated by the study for stationary solutions of the sixth-order parabolic differential equations

This equation arose in the formation of the spatial periodic patterns in bistable systems and is also a model for describing the behaviour of phase fronts in materials that are undergoing a transition between the liquid and solid state.Especially,forf(x,u)=u?u3it was studied by Gardner and Jones[7]as well as by Caginalp and Fife[4].
Iffis an even 2L?periodic function with respect tox,and odd with respect tou,to get the 2L?stationary spatial periodic solutions of(1.3),one turns to study the two points boundary value problems(1.1)and boundary condition(1.4)

The 2L?periodic extensionof the odd extension of the solutionuof problems(1.1)and(1.4)to the interval[?L,L]yields a 2L?spatial periodic solutions of Eq.(1.3).
At the same time,in investigating such spatial patterns,some other high-order parabolic differential equations appear,such as the extended Fisher-Kolmogorov(EFK)equation

proposed by Coullet,Elphick and Repaux in 1987 as well as by Dee and Van Saarlos in 1988 and Swift-Hohenberg(SH)equation

proposed in 1977.
Gyulov,Morosanu and Tersian[6]has studied the existence and multiplicity of nontrivial solution of BVP(1.1)-(1.2)by using variational tools,including two Brezis-Nirenberg’s linking theorems.In addition,S.Tersian and J.Chaparova[15]obtain the periodic and homolinic solutions by using minimization theorem,a multiplicity result using Clark’s theorem and a mountain-pass theorem of Brezis-Nirenberg.
In much the same time,the existence of spatial periodic solutions of both the EFK equation and the SH equation was studied by Peletier and Troy[3],Peletier and Rottsch¨afer[5],Tersian and Chaparova[8]and other authors.Recently,many authors(see[1],[2],[3])studied the following fourth-order periodic boundary value problem
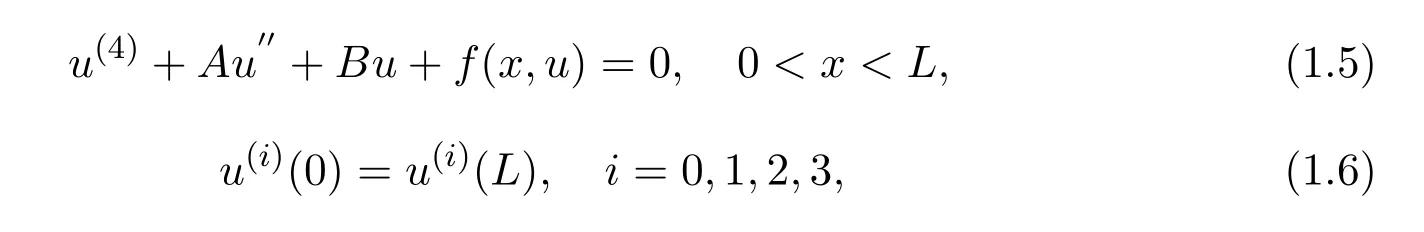
then directly obtained the periodic solution.The method used in those papers are maximum principle and the monotone method in presence of lower and upper solutions.
On the other hand,the positive solutions of fourth-order periodic boundary value problems(1.5)-(1.6)has been studied extensively by using the fixed point theorem(see[8],[9],[10]).Here we mention the paper of Yao[16]in which the author introduced control functions and then used the fixed point index theory on cone to study the problem(1.5)-(1.6).
The purpose of this paper is using the idea of[16]to investigate the existence results of positive solutions for PBVP

whereα,β,γandfsatisfy the following assumptions.
(H1)f:[0,1]×[0,∞]→[0,∞]is a continuous function.
(H2)α,β,γ∈R and satisfy

Here,a positive solutionu*of(1.7)satisfiesu*(t)>0,t∈[0,1].By drawing into new control functions,we will establish some existence criterion for(1.7).The existence criterion shows that problem(1.7)has at least one positive solution provided the growth rates of nonlinear termf(t,u)are appropriate on some bounded subsets of its domain.The main ingredient is the fixed point index theory on cones.And we will prove the existence ofnand infinitely many positive solutions,wherenis an arbitrary natural number.Besides,we also consider the nonexistence.
To be convenient,we introduce the following notations:
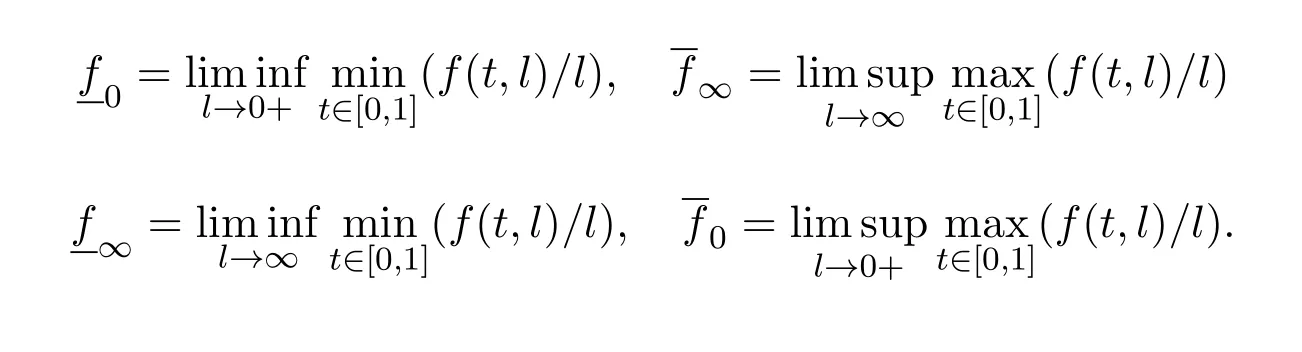
2 Preliminaries
We will use the Banach spaceC[0,1]equipped with the sup norm.Denote

wheren≥2,ai∈R.
We saynth-order operatorLnis inverse positive(inverse negative)in space

ifLn u≥0 foru∈Fnimpliesu≥0(u≤0),andLnis strongly inverse positive(strongly inverse negative)in spaceFnifLn u≥0 foru∈Fnimpliesu≡0 oru(t)>0(u(t)<0)for everyt∈[0,1].It is well known[10,11]that second order operatorL2,λ=u′′?λuis strongly inverse negative inF2forλ>0.
Lemma 2.1Assume(H2)holds.Then the operatorL6u=u(6)+γu(4)?βu′′+αuis strongly inverse positive inF6.
ProofSuppose?=18αβγ?β2γ2+4αγ3+27α2?4β3≤0.Then we have polynomialλ6+γλ4?βλ2+α=(λ2?λ1)(λ2?λ2)(λ2?λ3),whereλ1,λ2,λ3are the real-root ofP(λ)=λ3+γλ2?βλ+α.LetD=d/dtandIbe the identity operator,then we have the decomposition

Sinceα>0,by Vieta Theorem,we haveλ1λ2λ3<0.Thus,it is not restrictive to assumeλ1<0.
Ifλ2,λ3<0,sinceγ<3π2,3π4?2γπ2?β>0,α/π6+β/π4+γ/π2<1,it follows that?π2<λ1λ2λ3<0.By Lemma 2 in[7],D2?λi I(i=1,2,3)is strongly inverse positive inF2.ThusL6is strongly inverse positive inF6.
Ifλ2,λ3>0,thenD2?λi I(i=2,3)is strongly inverse negative inF2.By Lemma 2 in[7],D2?λ1Iis strongly inverse positive inF2.From(2.1)we obtain thatL6is strongly inverse positive inF6.
The proof is completed.
Consider the sixth-order linear problem

By Lemma 1 in[10],the problem has a unique continuous solutionu0(t)andu0(t)>0,0≤t≤1.Let

For given constantsα,β,γ,the minimummand maximumMcan be computed explicitly.
Denote

Then

Letσ=mM?1.Define the coneKof nonnegative functions inC[0,1]by

Forr>0,we denote?r={u∈K:‖u‖ Leth∈C[0,1].By Lemma 1 in[10],the linear boundary value problem associated with has a unique solutionu,which is given by expression Define the operatorT:C+[0,1]→C+[0,1]as follows Lemma 2.2(i)T(K)?K,T:K→Kis completely continuous. (ii)If 0/=u*∈Kis a fixed point ofT,thenu*is a positive solution of(1.7). Proof(i)Letu∈K.From the latter inequality of(2.3)it follows that and therefore Using this and the former inequality of(2.3),we have which impliesT u∈K.ThusT(K)?K.The complete continuity ofTis obvious. (ii)It is easy to check thatu*is a solution of(1.7)and‖u*‖>0.Sinceu*∈Kimplies thatu*(t)≥σ‖u*‖,0≤t≤1,u*is a positive solution of(1.7). We will find the nonzero fixed point ofTinKby applying the following fixed point index theorems on cone(see[10]). Lemma 2.3(Guo-Lakshmikantham)Let X be a Banach space,Kbe a cone in X,T:K→Kbe a completely continuous operator. (i)IfμT u/=ufor anyu∈??cand 0<μ≤1,theni(T,?c,K)=1. Lemma 2.4(Kronecker theorem) If deg(f,?,p)/=0,then the equationf(x)=phas a solution in?. We draw into the control functions In geometry,?(l)expresses the maximal growth rate offon boundary set[0,1]×[σl,l],ψ(l)expresses the minimal growth rate offon boundary set of[0,1]×[σl,l].We also let the limits Lemma 2.5(1)If<α,then<α. Proof(1)Letε=.Then there existsδ1>0 such thatf(t,c)≤(α?ε)c,(t,c)∈[0,1]×(0,δ1].Thus,for anyl∈(0,δ1],?(l)≤α?ε<α.Therefore,<α. (4)Letε=?α].Then there existsδ4>0 such thatf(t,c)≥(α+ε)c,(t,c)∈[0,1]×[δ4,∞].Thus,for anyl∈[δ4,∞],ψ(l)≥α+ε>α.Therefore,>α. The proofs of(2)and(3)are similar. We obtain the following existence results. Theorem 3.1Assume that there exist two positive numbersa,bsuch that?(a)<α,ψ(b)>α.Then problem(1.7)has at least one positive solutionu*∈Ksatisfying min{a,b}<‖u*‖ ProofIt is easy to seea/=b.We may assumea First,we proveμT u/=ufor anyu∈??aand 0<μ≤1.If not,there existu0∈??aand 0<μ0≤1 such thatμ0T u0=u0.It followsσa=σ‖u0‖≤u0(t)≤a,0≤t≤1 andf(t,u0(t))≤?(a)u0(t)<αu0(t),0≤t≤1.By the definition ofT,u0(t)satisfies the differential equation Integrating this equation from 0 to 1 and noticing we get Second,ifu∈??b,we haveσb=σ‖u‖≤u(t)≤b,0≤t≤1 andf(t,u(t))≥ψ(b)u(t)>αu(t),0≤t≤1.It follows that Next,we proveμT u/=ufor anyu∈??bandμ≥1.If not,there existu1∈??bandμ1≥1 such thatμ1T u1=u1.By the definition ofT,u1(t)satisfies the differential equation Integrating this equation from 0 to 1,we get From(3.1)and(3.2)it follows that By the Kronecher existence theorem,we assert that the operatorThas at least one fixed pointu*∈?b.It implies that problem(1.7)has at least one positive solutionu*∈Kanda<‖u*‖ From Theorem 3.1 we immediately obtain the following. Corollary 3.2Assume that<αand>α.Then problem(1.7)has at least one positive solutionu*∈K. Corollary 3.3Assume that one of the following conditions holds, Then problem(1.7)has at least one positive solutionu*∈K. Applying Corollary 3.3 and Lemma 2.5 we obtain. Theorem 3.2Suppose that one of the following conditions holds, Then problem(1.7)has at least one positive solution. We denote the integer part oflby[l]below. Theorem 4.1Assume that there existn+1 positive numbersa1 (i)?(a2k?1)<α,k=1,2,···,andψ(a2k)>α,k=1,2,···, (ii)ψ(a2k?1)>α,k=1,2,···,and?(a2k)<α,k=1,2,···,Then the problem(1.7)has at leastnpositive solutionsK,k=1,2,···,nsatisfyingak< ProofBy Theorem 3.1 we see that(1)has a positive solution∈Ksuch that We have the following existence results for two positive solutions. Corollary 4.2Assume that (ii)there exists a positive numberbsuch thatψ(b)>α. Then the problem(1.7)has at least two positive solutions∈Ksatisfying 0<<+∞. Corollary 4.3Assume that (ii)there exists a positive numberasuch that?(a)<α. Then the problem(1.7)has at least two positive solutions∈Ksatisfying 0<<+∞. We also have the following existence results for three positive solutions. Corollary 4.4Assume that(i)<αand>α(particularly,<αand>α). (ii)there exists positive numbersb Corollary 4.5Assume that (ii)there exists positive numbersa Then the problem(1.7)has at least three positive solutions∈Ksatisfying<+∞. Theorem 5.1Assume that<αand>α.Then problem(1.7)has a sequence of positive solutions→0. ProofSince<αand>α,there exist sequencesak→0,bk→0 such that?(ak)<α,ψ(bk)>α,k=1,2,···.We may assumea1>b1>a2>b2>···>ak>bk>···without loss of generality.By Theorem 3.1,the proof is completed. Similarly,we can prove the following Theorem 5.2. Theorem 5.2Assume that<αand>α.Then problem(1.7)has a sequence of positive solutionsKsatisfying→+∞. We also have the following nonexistence result. Theorem 6.1Let 0 (i)?(l)<α,l∈(a,b). (ii)ψ(l)>α,l∈(a,b). Then problem(1.7)has not positive solutionu*∈Ksatisfyinga<‖u*‖ ProofIt is enough to prove case(ii).Supposeu*∈Kis solution of(1.7)such thata<‖u*‖ Noticing thatσ‖u*‖≤u*(t)≤‖u*‖,t∈[0,1],we have On the other hand,sinceu*is a solution of problem(1.7),we have Integrating this equation from 0 to 1,we get Example 7.1Let us consider the following problem whereα,β,γsatisfy(H1)andfis defined by Then it is easy to verify that Therefore,from Theorem 5.1 it follows that problem(7.1)has a sequence of positive solutionsKsatisfying→0. Example 7.2Let us consider the following problem whereα,β,γsatisfy(H1)andfis defined by Then it is easy to verify that Therefore,from Theorem 5.2 it follows that problem(7.2)has a sequence of positive solutionsKsatisfying→∞. Example 7.3Let us consider the following problem It is clear thatα,β,γsatisfy(H1).Furthermore,we have Therefore,from Theorem 6.1 it follows that problem(7.3)has no positive solutionu*∈Ksatisfyinga<‖u*‖






3 Existence



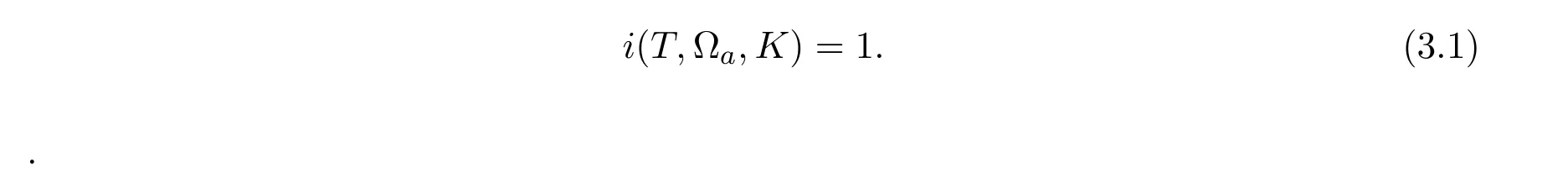





4 Multiplicity
5 Infinite Solvability
6 Nonexistence




7 Examples








 南京大學(xué)學(xué)報(bào)(數(shù)學(xué)半年刊)2021年1期
南京大學(xué)學(xué)報(bào)(數(shù)學(xué)半年刊)2021年1期
