A FRACTIONAL NONLINEAR EVOLUTIONARY DELAY SYSTEM DRIVEN BY A HEMI-VARIATIONAL INEQUALITY IN BANACH SPACES?

Yunhua WENG(翁云華)Xuesong LI(李雪松)Nanjing HUANG(黃南京)

Department of Mathematics,Sichuan University,Chengdu 610064,China E-mail:yunhuaweng@outlook.com;xuesongli78@hotmail.com;nanjinghuang@hotmail.com;njhuang@scu.edu.cn

Abstract This article deals with a new fractional nonlinear delay evolution system driven by a hemi-variational inequality in a Banach space.Utilizing the KKM theorem,a result concerned with the upper semicontinuity and measurability of the solution set of a hemivariational inequality is established.By using afixed point theorem for a condensing setvalued map,the nonemptiness and compactness of the set of mild solutions are also obtained for such a system under mild conditions.Finally,an example is presented to illustrate our main results.

Key words fractional differential variational inequality;fractional nonlinear delay evolution equation;hemi-variational inequality;condensing map;KKM theorem;fixed point theorem

1 Introduction

It is well known that the differential variational inequality(for short,DVI),introduced initially by Aubin and Cellina[2]in 1984,was systematically studied by Pang and Stewart[35]infinite dimensional Euclidean spaces in 2008.As pointed out by Pang and Stewart[35],DVI plays an important role in describing issues pertaining to many areas,such as fluid mechanical problems,contact friction,engineering operation research,economical dynamics,dynamic traffic networks problems,obstacle problems for contacting bodies,and so on.Various theoretical results,numerical algorithms and applications have been studied for DVIs.For example,by adopting a method of differential inclusions with regard to the set-valued map,Li et al.[22]proved the existence theorems of a class of DVIs and established the convergence result on a time-series for solving DVIs involving an initial condition.By utilizing Mosco convergence,Gwinner[13]obtained a stability theorem for a new class of DVIs concerning perturbation parameters for the data.Some related works concerned with DVIs in finite dimensional spaces can be found in [19–21,23,31,36].Recently,Liu and Zeng [24],Liu et al.[27],Liu et al.[26],and Liu et al.[25]discussed the existence of solutions as well as the topological structure of the solution set for DVIs in infinite-dimensional Banach spaces under some mild conditions.

On the other hand,as a field of applied mathematics,fractional calculus can be used to handle calculus of arbitrary order.During the last 20 years,fractional calculus has been widely used in almost every field of physics,engineering,biology,and economics (see [3–5,14,34]).It is noticeable that one of the major advantages of fractional order models is that they can be deemed as the super set of integer order calculus.Thus,there is great potential for fractional calculus to achieve what integer order calculus cannot.In 2015,Ke et al.[18]proved the nonemptiness of the decay solution set for a new class of DVIs regarding fractional order derivatives in finite dimensional spaces.Recently,by using the difference method,together with the surjectivity theorem of set-valued maps and properties of the Clarke subdifferential,Zeng et al.[41],Zeng and Mig′orski[42]discussed fractional differential elliptic hemi-variational inequality and fractional differential parabolic hemi-variational inequality in Banach spaces,respectively.Very recently,Mig′orski and Zeng [30]investigated a class of fractional DVIs in Banach spaces and obtained the existence theorem of solutions for their model by employing the discrete approximation approach.

We note that,in some practical situations,it is necessary to consider some dynamical systems driven by delay evolution equations because time delay is ubiquitous in most physical,chemical and biological systems such as population dynamics,optical bistable devices,electromechanical systems,predator-prey models,and physiological systems (see,for example,[8,15,32,39]and the references therein).Recently,Wang et al.[38]investigated a class of delay DVIs consisting of a system of variational inequalities and delay differential equations in finite dimensional Euclidean spaces.Due to the fact that a lot of application problems arising in engineering and physics can be described more precisely by differential equations in infinite dimensional spaces [1],it is important and interesting to investigate fractional DVIs involving time delay in infinite dimensional spaces.However,until now,there has never been a study on fractional differential hemi-variational inequalities involving state-dependent delay in infinite dimensional spaces.The main purpose of this article is to study a new fractional delay evolution system governed by a hemi-variational inequality (for short,FDESHVI) in Banach spaces under some mild conditions.

The rest of this article proceeds as follows:the next section presents some necessary preliminaries.In Section 3,we show that the solution set of a hemi-variational inequality is upper semicontinuious and measurable by employing the KKM theorem.In addition,by using the fixed point argument of the condensing set-valued map,we obtain the existence and compactness of the set of mild solutions for FDESHVI.Finally,we present an example to demonstrate our main results in Section 4.

2 Preliminaries

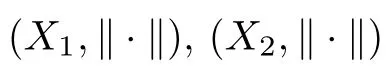
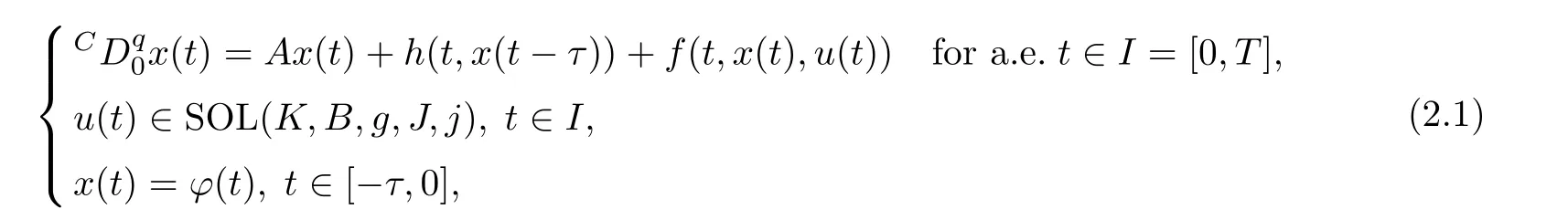
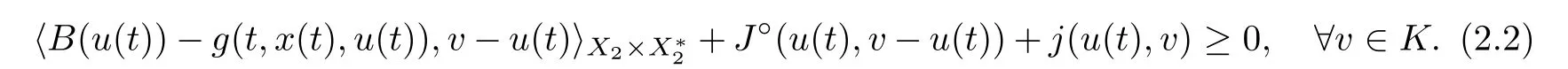
Some special cases of FDESHVI (2.1) are as follows:

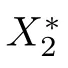
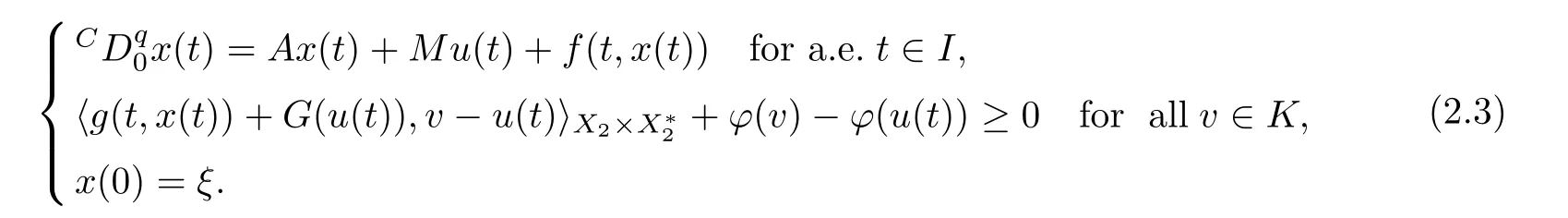
This was considered by Mig′orski and Zeng [30].Moreover,if α=1 and ?=0,then (2.3)reduces to the DVI considered by Liu and Zeng [28].

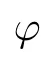
This was discussed by Ke et al.[18].

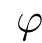
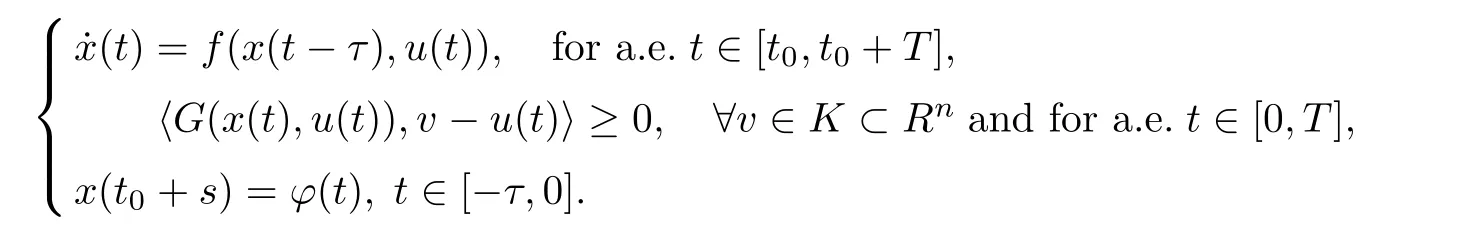
This was investigated by Wang et al.[38].

2.1 Set-valued analysis and measure of noncompactness (MNC)

Let W be a topological space.In the sequel,we denote the following:

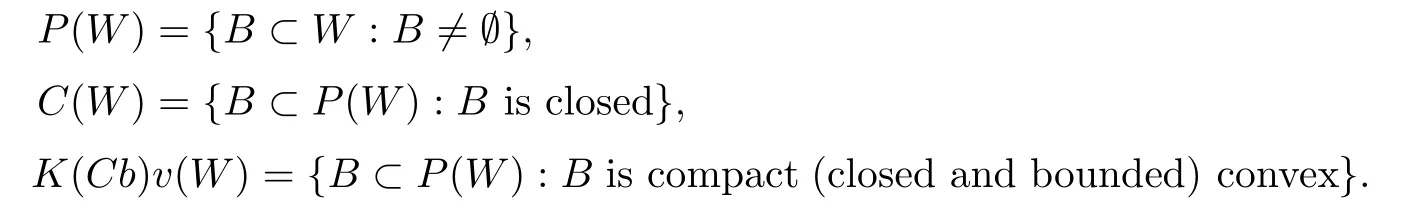
Definition 2.1

(see [17]) Let E be a Banach space.A function β :P(E)→Ris called an MNC in E if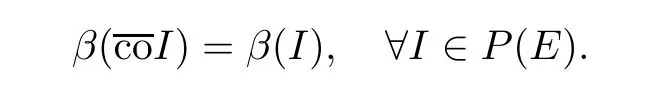

An MNC β is said to be

i) monotone if,for any I,I∈P(E),I?Iimplies that β(I)≤β(I);

ii) nonsingular if β(a ∪I)=β(I),?a ∈E,?I ∈P(E);

iii) invariant with reference to union with compact set if β(K∪I)=β(I)for every relatively compact set K ?E and I ∈P(E);

iv) semi-additive if β(I+I)≤β(I)+β(I);

v) regular if β(I)=0 is equivalent to that I is relative compact.

A representative instance of MNC is the Hausdorff MNC ν(·):

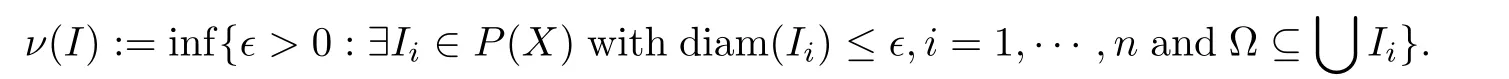
We also need to repeat the definition of MNC in Banach space C([0,T];E)(see[17]),which is given by

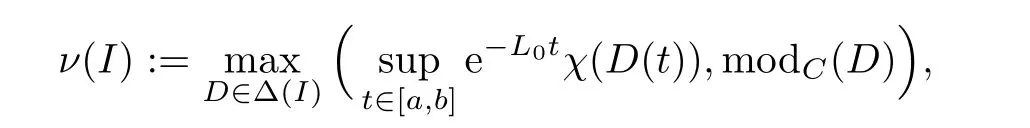
where ?(I) denotes the group of all countable subsets of I,where Lis a constant,and

Clearly,MNC ν is monotone nonsingular and regular.

In what follows,we turn to some preliminaries of set-valued analysis.Let Eand X be two metric spaces.

Definition 2.2

A set-valued map F :E→P(X) is said to be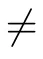

ii) lower semicontinuous(l.s.c.) if,for every closed set W ?X,the small preimage F(W)defined by F(W)={y ∈E:F(y)?W} is a closed subset of E;

iii) continuous if F is both u.s.c.and l.s.c..

iv) closed if G={(y,z):y ∈E,z ∈F(y)}?E×X is closed;

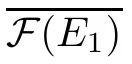
Lemma 2.3

(see[12,Proposition 14.5]) Let E and V be two Hausdorff topological spaces.Assume that the set-valued map G:E →P(V) satisfies the following conditions:

i) there exists a compact set K ?V such that G(E)?K;

ii) the graph of G is closed.

Then G is u.s.c..

Definition 2.4

A set-valued map F :Z ?E →P(E)is said to be condensing in relation to MNC β (or β-condensing) if,for every bounded subset I ?Z,the relation β(I) ≤β(F(I))entails that I is relatively compact in Z.

Lemma 2.5

(see[17,Corollary 2.2.1]) Let D be a nonempty,bounded,and closed subset of a Banach space E.If Σ:E →K(E) is k-Lipschitz (0 Lemma 2.6

(see [7,Theorem 5.1.5]) Let D ∈Cv(E),with E being a Banach space and F :D →Cv(D) being a closed u.s.c.β-condensing map.Then,FixF,the set of fixed point of F,is nonempty.

Lemma 2.7

(see [17,Proposition 3.5.1]) Let D ∈C(E),with E being a Banach space and F :D →K(E) being a closed map such that F is β-condensing when it is restricted to any bounded subset of D.Then FixF is compact,provided that it is bounded.

Definition 2.8

(see[24]) Let X and V be two Banach spaces and let I ?R be an interval.The set-valued map G given by G:I×X →P(V)is said to be superpositionally measurable if,for any measurable set-valued map Z :I →K(X),the set-valued map M :I →P(V) defined by M(t)=G(t,Z(t)) is measurable.

Lemma 2.9

(see [24,Theorem 2.3]) If G:I ×X →P(V) is u.s.c.,then G is superpositionally measurable.

Definition 2.10

(see [10]) Let X be a Banach space and J :X →R a locally Lipschitz function.The generalized directional derivative of J at x ∈X in the direction y ∈X is defined by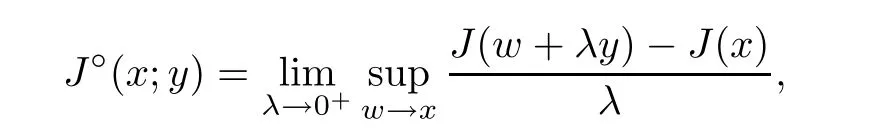

and the generalized gradient of J :X →R is defined as

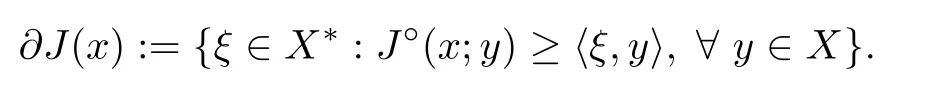
Proposition 2.11

(see [10,proposition 2.1.2]) Let J :X →R be a locally Lipschitz function with the Lipschitz constant L>0 near x ∈X.Then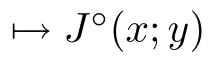

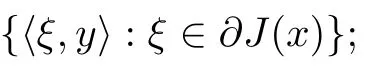
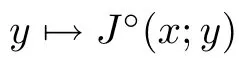
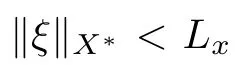
Lemma 2.12

(see [11,Lemma 2.4],KKM Theorem) Let Y be a Hausdorff topological space and let K ?Y be nonempty.Assume that the set-valued map F :K →C(Y) meets the following two conditions:

(a) F is a KKM map,that is,for every {y,y,···,y}?K,one has

(b) there exists at least one y∈K such that F(y)∈Y is compact.

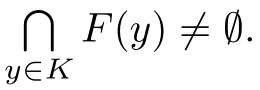
2.2 Fractional calculus

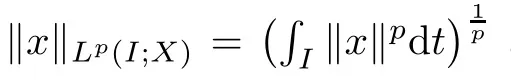
Definition 2.13

(see [16]) The fractional integral of order q >0 of a function x(t) ∈L([0,+∞);R) is defined by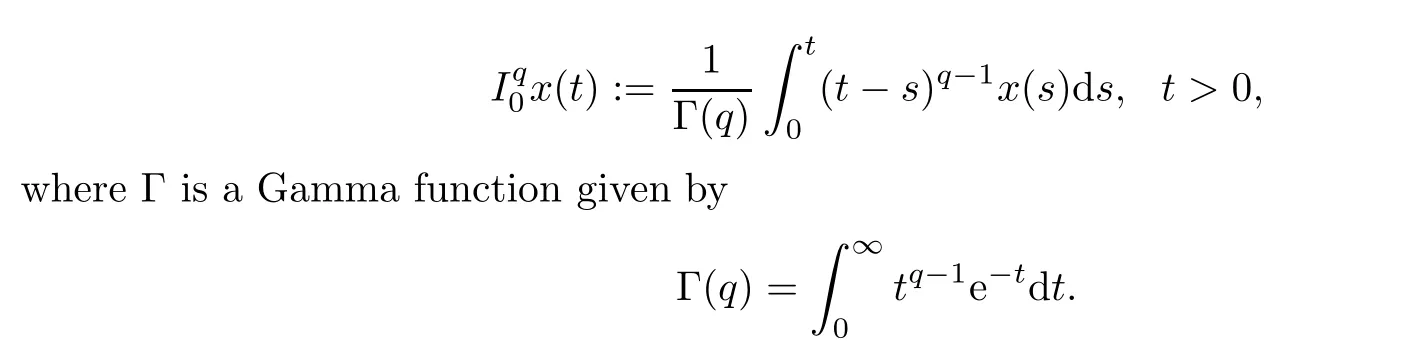

Definition 2.14

(see [16]) For a given function x(t)∈C([0,+∞);R),the Caputo fractional derivative of order q ∈(n ?1,n) is defined by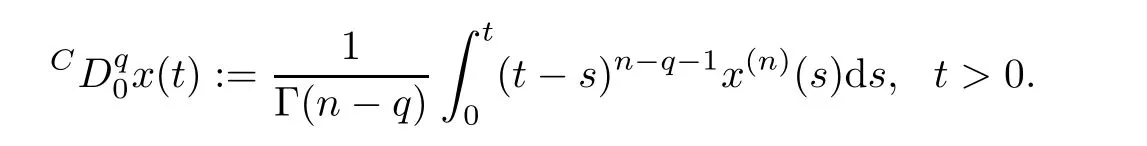

Note that,if x(t) has values in an abstract space X,then the integrals appearing in Definitions 2.13 and 2.14 are understood in Bochner’s sense.

According to [33,40],the mild solution of FDESHVI is defined as follows:

Definition 2.15

A pair(x,u)is said to be the mild solution of FDESHVI if x ∈C([?τ,T];X) and u:I →K is measurable such that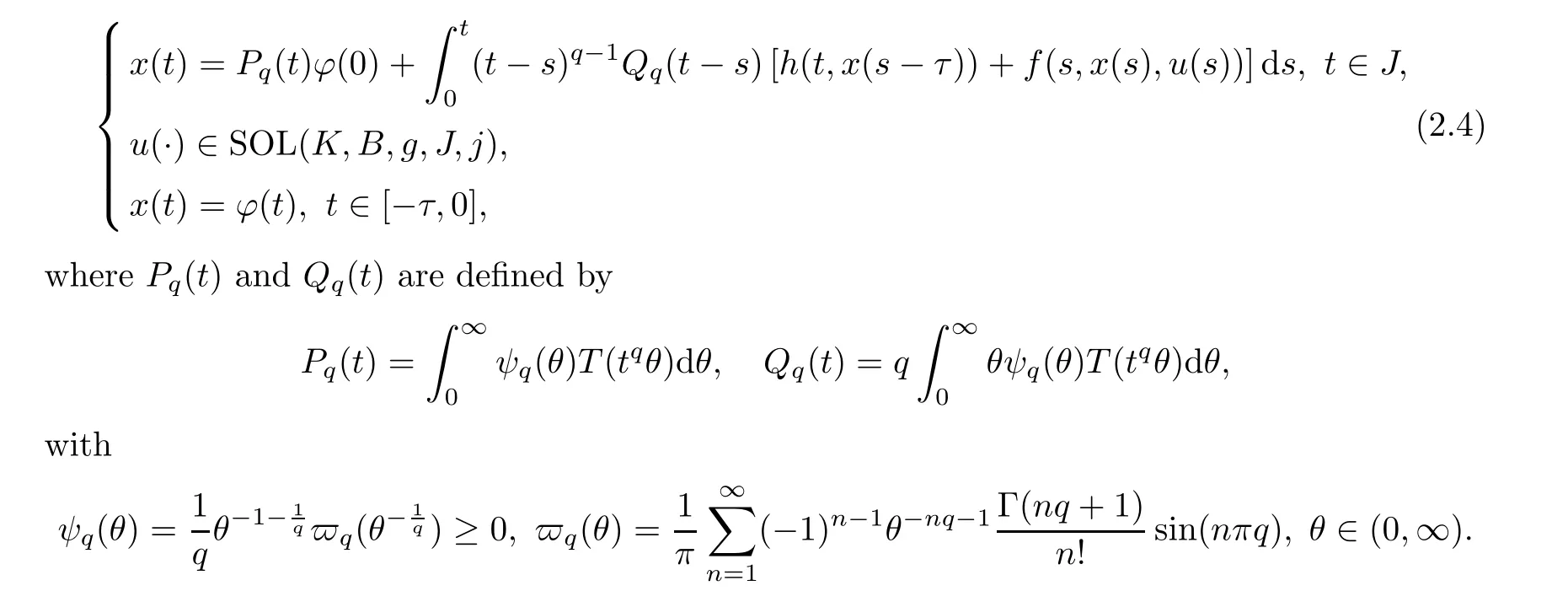

Following [26],if a pair (x,u) is a mild solution of FDESHVI,then x(t) is called the mild trajectory function and u(t) is called the variational control function.

Lemma 2.16

(see[40,Lemmas 3.2–3.4]) The operators Pand Qpossesses the following properties:

i) For any given t ≥0,P(t) and Q(t) are bounded linear operators such that,for any x ∈X,

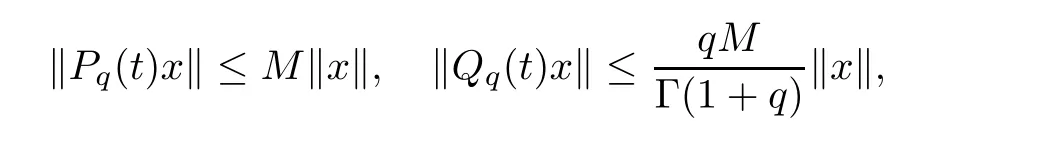
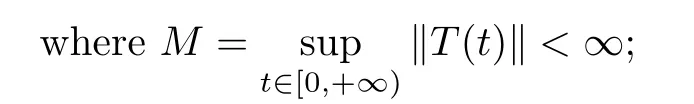
ii) {P(t),t ≥0} and {Q(t),t ≥0} are strongly continuous;

iii) For any t>0,if T(t) is compact,then P(t) and Q(t) are also compact.

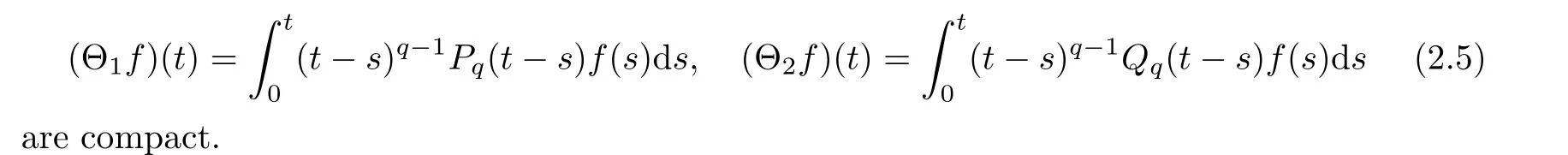
Lemma 2.18

(see [33,Theorem 2.3.2]) For t >0,{T(t)}is uniformly continuous provided that it is a compact C-semigroup.

3 Existence Results on Bounded Time Intervals

Let ν be the Hausdorff MNC on C([?τ,T];X).In order to obtain the existence results for FDESHVI,we need the following hypotheses:

In addition,if K is bounded,then the set of solutions of (3.1)is nonempty,convex,and closed.If K is unbounded,the above conclusion is also correct provided that there exist u∈K and r >0 such that

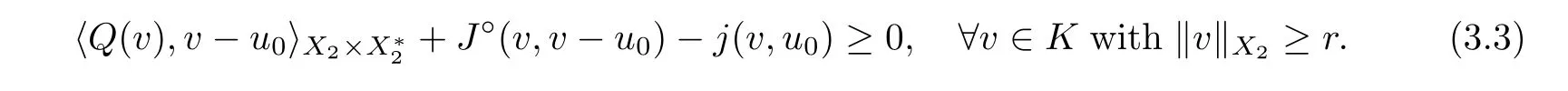
Proof

First,we show that (3.1) is equivalent to (3.2).For simplicity,let Sdenote the set of solutions of (3.1).If u ∈S,then,by Proposition 2.11(b),one has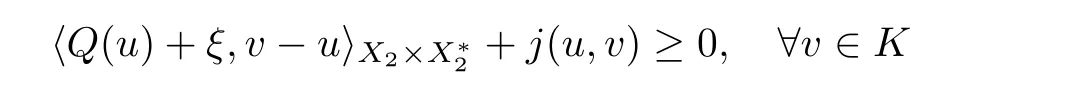

for some ξ ∈?J(u).Invoking the monotonicity of Q+?J,it follows from the above inequality that

Conversely,if u ∈K solves (3.2),then for any t ∈(0,1) and v ∈K,u=tv+(1 ?t)u ∈K thanks to the convexity of K.Thus,

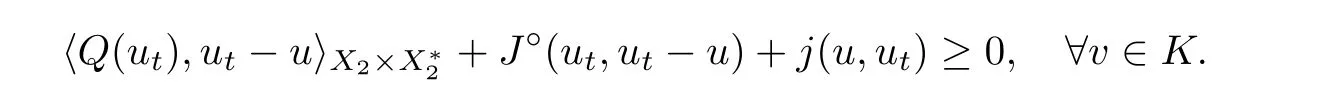
In view of (Hj)(ii),(iv) and Proposition 2.11(c),one has

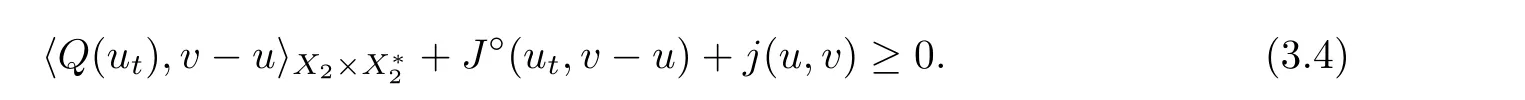
Applying (i),Proposition 2.11(a) and taking the limit as t →0,we have

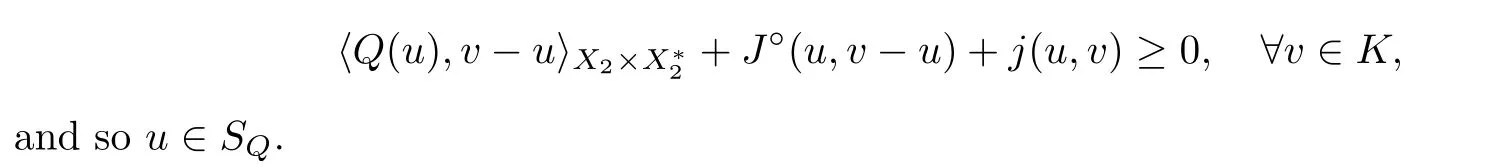
Secondly,we prove that Sis closed.Let u∈Sand u→u ∈X.According to the equivalence of (3.1) and (3.2),we have

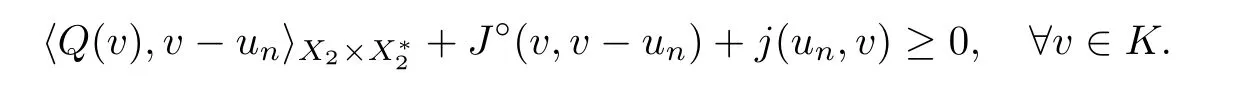
It follows from Proposition 2.11(a) and (Hj)(iii) that

This shows that

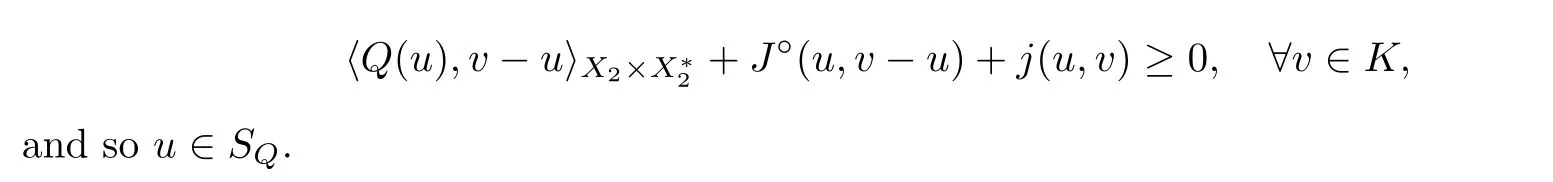
Thirdly,we show that Sis convex.Let u,u∈S.Then

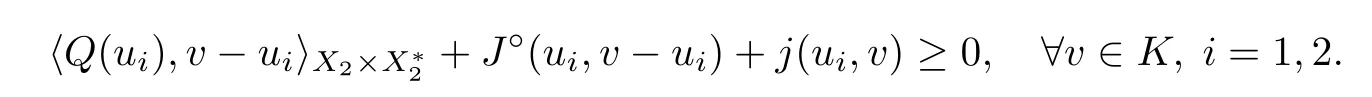
By condition (iii),one has

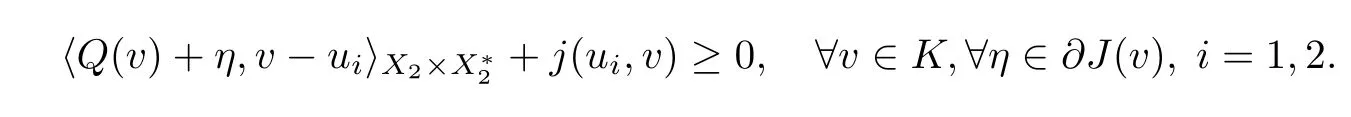
This implies that u=tu+(1 ?t)u∈K for all t ∈(0,1).From (Hj)(iii) and Proposition 2.11(b),for any v ∈K,there is η∈?J(v) such that

This implies that u∈S,and so Sis convex.

Fourthly,we claim that Sis nonempty.The proof is divided into two cases.

Case 1

If K is bounded in X,we consider the set-valued map F :K →P(K) defined by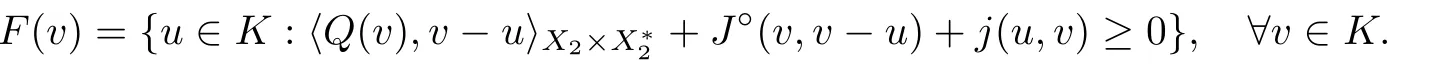

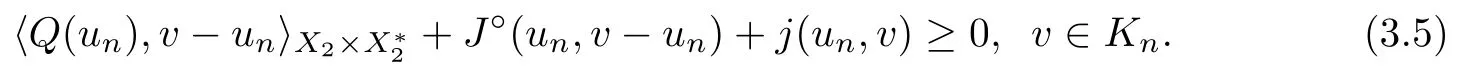
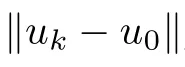
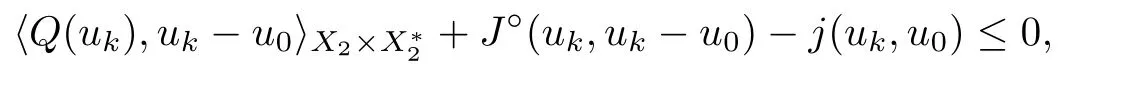
which is a contradiction to (3.3).This shows that the claim holds.Thus,for every u ∈K,there exists λ>0 small enough such that

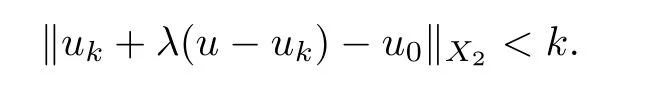
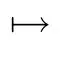
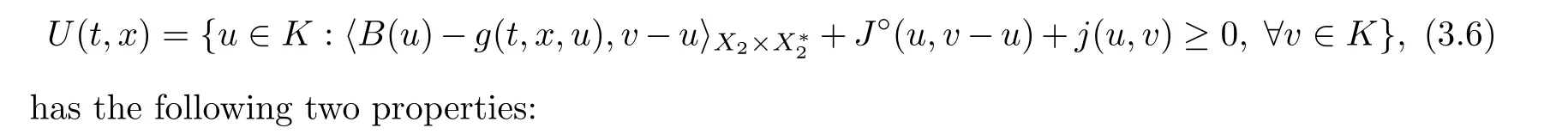
(i) U is u.s.c.;

(ii) U is superpositionally measurable.

Next,we show that,for any closed subset D ?K,the set

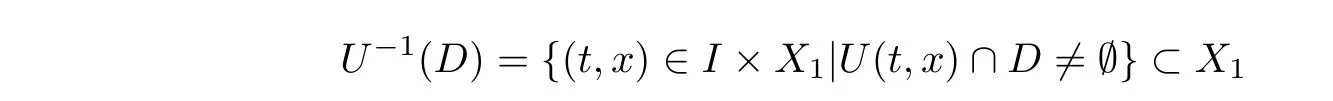
is closed.In fact,for any sequence {(t,x)} ?U(D) with (t,x) →(t,x),we can choose u∈U(t,x)∩D.According to (3.6),we have

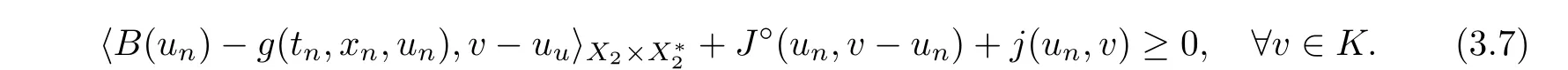
The compactness of K yields that there exists a subsequence of {u} denoted again by {u}such that u→u ∈D.Letting n →∞in (3.7),from conditions (Hg),(HB),(HJ),and(Hj)(iii),one has

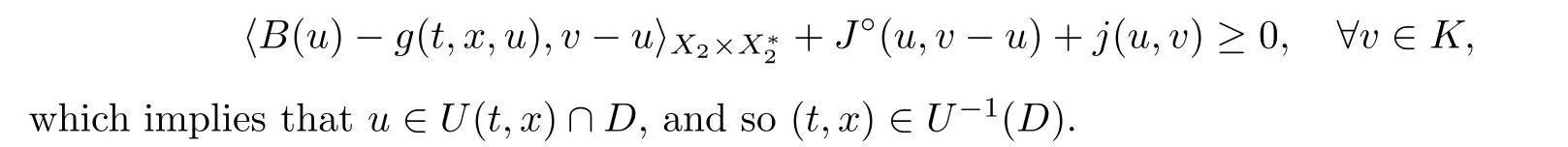
Next we define a set-valued map F :I ×X→P(X) by setting

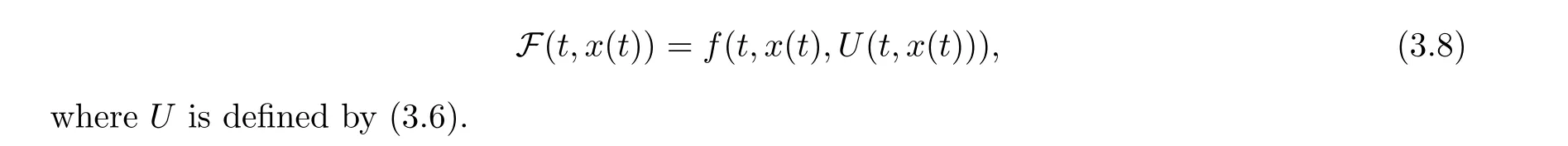
Lemma 3.3

(see [26],Lemma 3.6) Assume that all the conditions of Theorem 3.2 and(Hf) are fulfilled.Then F possesses the following properties:

(F) For every (t,x)∈I×X,F(t,x)∈Kv(E);

(F) F(·,x) admits a strongly measurable selection for every x ∈X;

(F) For every t ∈I,F(t,·) is u.s.c..

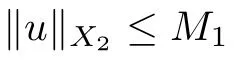
where F(t,x) is defined by (3.8).

Lemma 3.5

Under the same conditions as those of Lemma 3.3,the set P(x)is nonempty and convex for every x ∈C(I;X).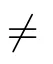

Lemma 3.6

Assume that condition (Hf) holds and that {x} ?C(I;X) with f∈P(x) such that x→xand f?f ∈L([0,T]).Then f ∈P(x).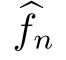

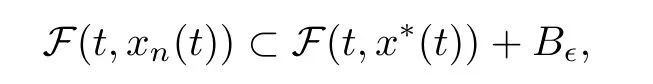
with ?>0 being a given number and B?Xbeing a ball centered at origin with a radius of ?.Thus,

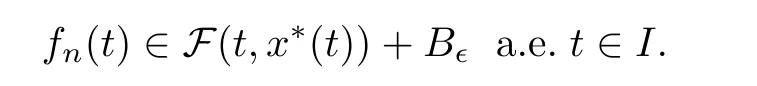
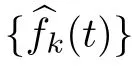
Now,we will present the main results of this section.

Theorem 3.7

Assume that (HW),(Hf),(Hh),and (HT) hold.Then,under the same conditions as those of Theorem 3.2,FDESHVI (2.1) has at least one mild solution.Moreover,the set of mild trajectory functions of FDESHVI is compact in C([?τ,T],X).

Proof

For any x ∈C([?τ,T],X),we define a set-valued map Σ as follows: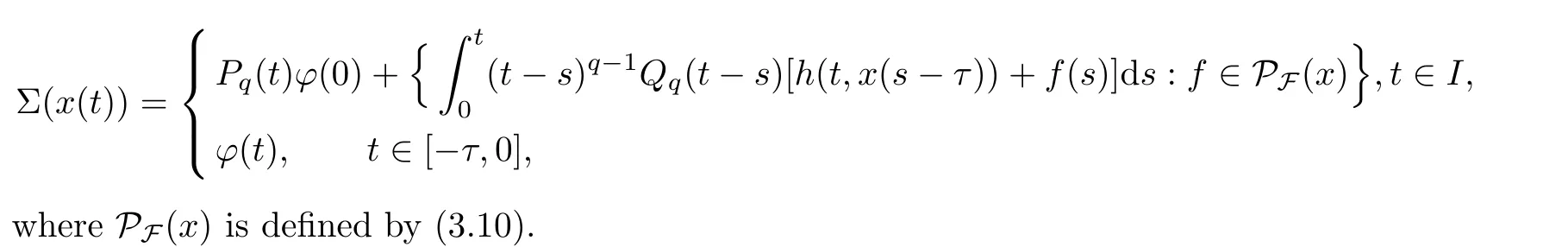

We first show that Σ :C([?τ,T],X)→P(C([?τ,T],X)).Theorem 3.2 ensures that the set-valued map U :I×X→Kv(K) is superpositionally measurable.According to Filippov’s implicit lemma [17],for any x ∈C(I,X),there is a measurable selection u(t)∈U(t,x(t) such that

Thus,according to Lemma 3.5,we know that Σ(x) is well-defined.Moreover,Lemma 2.17 implies that Σ(x)?C([?τ,T],X),and so Σ:C([?τ,T],X)→P(C([?τ,T],X)).

In order to prove the existence of a mild solution for FDESHVI,it suffices to show that Σ admits a fixed point.We will prove that the set-valued map Σ fulfills all the conditions of the Lemmas 2.6 and 2.7.The proof is proceeds in three steps.

Step 1

For every x ∈C([?τ,T],X),Σ(x) is compact and convex.

In light of Lemmas 2.17 and 3.5,it is easy to verify that Σ(x)is compact.Let z,z∈Σ(x).Then there are f,f∈P(x) such that

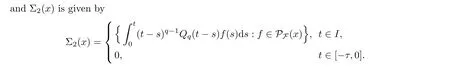
By Lemma 2.5,we need only to show that Σis contractive and that Σis u.s.c.and compact.We divide the proof into 5 claims.

Claim 1

Σis contractive on B.For any x∈Bwith i=1,2 and t ∈I,it follows from(Hh(ii)) that

Claim 2

Σ(x) is uniformly bounded on B.According to the proof of Step 2,one can obtain this claim.

Claim 3

{Σ(x) :x ∈B} is equicontinuous.For this purpose,we discuss the following two situations:

Case 1

For any x ∈Band ? >0,if t=0,0

We show that for any t ∈[?τ,T],Υ(t)={Σx(t) :x ∈B} ?Xis relatively compact.For any t ∈[?τ,0],it is easy to see that Υ(t)={0}is compact and so we only need to consider t ∈(0,T].For any t ∈(0,T],x ∈B,and z ∈Σ(x),there is a function f ∈Psuch that

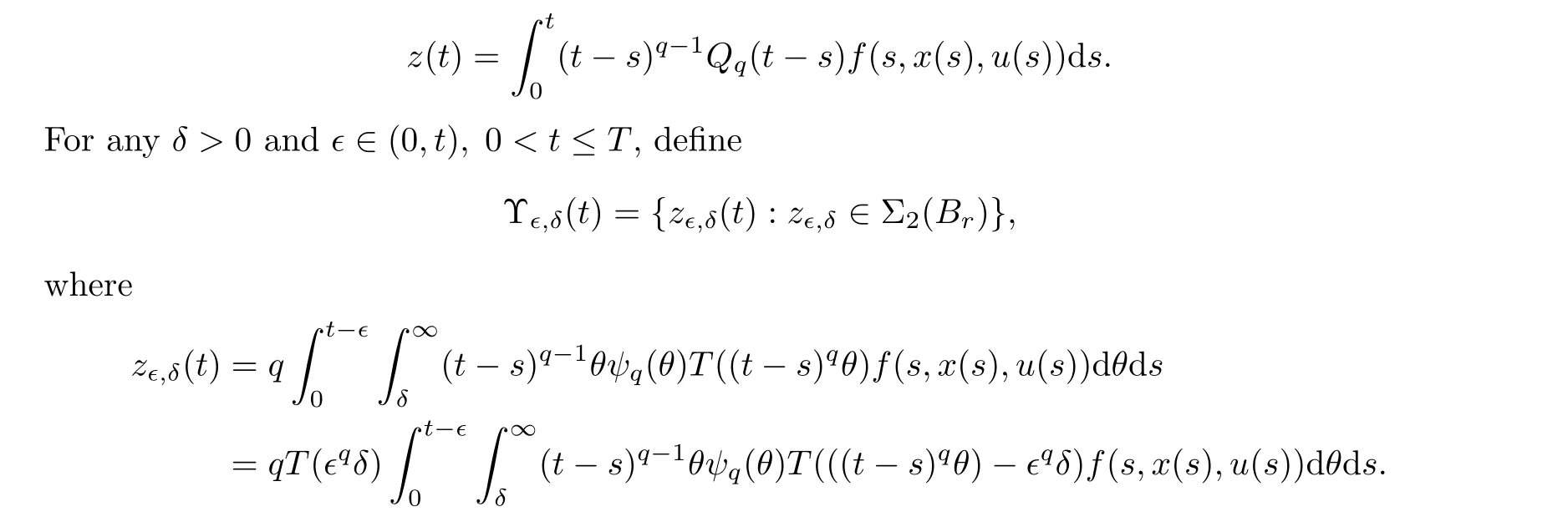
For any ? ∈(0,t) and δ >0,due to the compactness of operator T(?δ)(?δ >0),it is easy to see that Υ(t)?Xis relatively compact.

From condition (Hf)(ii),Lemma 2.16,and H?lder’s inequality,one has

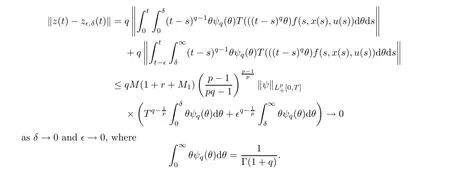
Hence,one can find a relatively compact set close to the set Υ(t)arbitrarily,and so Υ(t)?Xis also relatively compact for t>0.Now the Ascoli-Arzela theorem [6,Proposition 1.7.3]implies that {Σx(t):x ∈B}?Xis relatively compact,and so Claim 4 holds.

Claim 5

Σis closed.

Let x→x and z∈Σxwith z→z.We prove that z ∈Σx.In fact,z∈Σx?Bimplies that there exists f∈P(x) satisfying,for every t ∈I,that

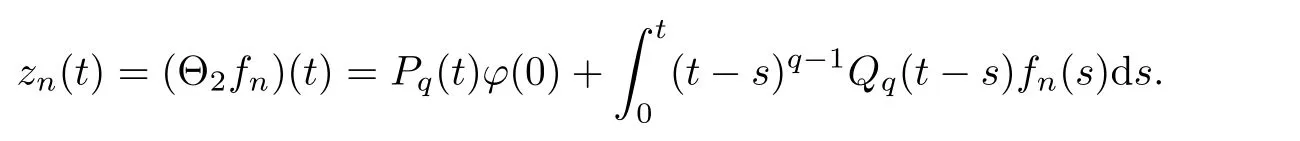
According to (Hf)(ii),we obtain the boundedness of{f}.Due to the reflexivity of L(I;X),we can assume that f?f in L(I;X).As x→x ∈C(I;X) ?L(I;X),it follows from Lemmas 2.17 and 3.6 that

Thus,Claim 5 is true.

By Claims 4 and 5,the upper semicontinuity of Σis a direct result of Lemma 2.3.Therefore,from Claims 1 to 5,we know that Σ=Σ+Σis u.s.c.and condensing.

4 An Example

Let X=L([0,π]),X=R,and K=[2π,5π].Define an operator A:D(A) ?X→Xas Ax=xwith the domain D(A) defined by

D(A)={x ∈X:x,xare absolutely continuous,x∈X,x(t,0)=x(t,π)=0}.According to [43],one can rewrite A as

猜你喜歡

雪松南京

南京比鄰

中國(guó)自動(dòng)識(shí)別技術(shù)(2023年6期)2024-01-12 08:13:22

趙雪松書法作品

詩(shī)潮(2023年11期)2023-12-01 23:24:36

“南京不會(huì)忘記”

環(huán)球時(shí)報(bào)(2022-08-16)2022-08-16 15:13:53

基于改進(jìn)DBSCAN的異常電池識(shí)別

汽車實(shí)用技術(shù)(2022年3期)2022-02-23 12:47:58

趙雪松書法作品

詩(shī)歌月刊(2019年7期)2019-08-29 01:46:48

牛雪松教授簡(jiǎn)介

沈陽體育學(xué)院學(xué)報(bào)(2018年2期)2018-08-02 00:36:38

南京·九間堂

金色年華(2017年8期)2017-06-21 09:35:27

又是磷復(fù)會(huì) 又在大南京

中國(guó)化肥信息(2016年41期)2016-05-17 04:25:59

南京：誠(chéng)實(shí)書店開張

新高考·英語進(jìn)階(高二高三)(2016年1期)2016-03-05 09:05:18

趙雪松書法作品

山花(2015年20期)2015-12-20 09:04:29

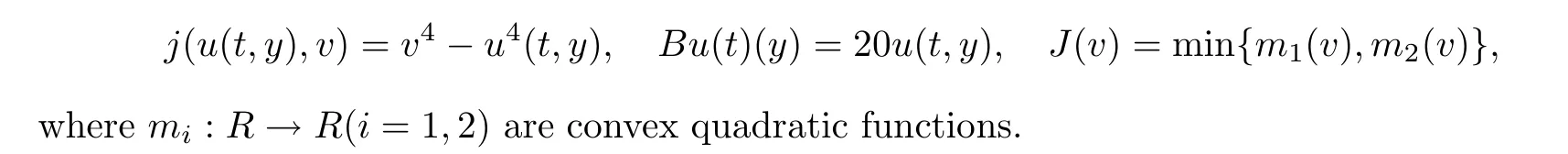
Acta Mathematica Scientia(English Series)2021年1期

Acta Mathematica Scientia(English Series)的其它文章

ON THE MIXED RADIAL-ANGULAR INTEGRABILITY OF MARCINKIEWICZ INTEGRALS WITH ROUGH KERNELS?

THE LOCAL WELL-POSEDNESS OF A CHEMOTAXIS-SHALLOW WATER SYSTEM WITH VACUUM?

UNDERSTANDING SCHUBERT’S BOOK(I)?

GLEASON’S PROBLEM ON FOCK-SOBOLEV SPACES?

THE EXISTENCE AND STABILITY OF STATIONARY SOLUTIONS OF THE INFLOW PROBLEM FOR FULL COMPRESSIBLE NAVIER-STOKES-POISSON SYSTEM?

ON THE CAUCHY PROBLEM FOR AW-RASCLE SYSTEM WITH LINEAR DAMPING?