一類四階常微分方程周期邊值問題的正解

王天祥,李永祥

(西北師范大學數學與統計學院,甘肅 蘭州 730070)

1 引言

本文討論四階非線性常微分方程

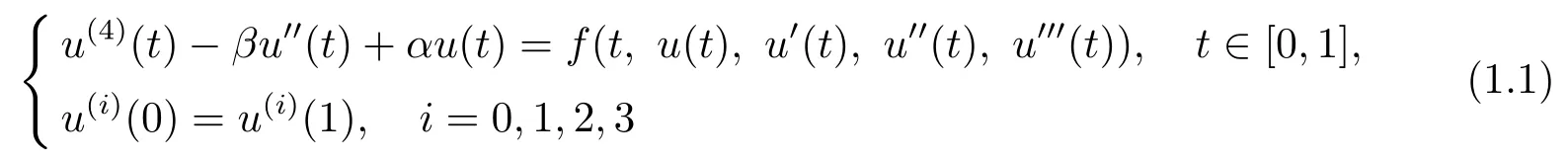
正解的存在性,其中f:[0,1]×[0,+∞)×R3→[0,+∞)連續(xù).該問題描述了靜態(tài)彈性梁在周期邊界條件下的形變,f中的未知函數項u表示梁形變的位移,u0表示隅角,u00表示彎矩,u000表示剪切力剛度.而在彈性梁模型中,只有正解才有實際意義.

四階常微分方程周期邊值問題在非線性振動,流體力學和非線性彈性現象等諸多領域有著廣泛的應用,因而受到了許多學者的研究[1–16].主要應用的非線性分析的工具和方法有錐上的不動點指數理論 [1–3,6,16],Krasnoselskii不動點定理 [6,7,15],單調迭代技巧[4,5,9,12–14],拓撲度方法 [8]等.

對非線性項f不含導數項的簡單四階周期邊值問題(PBVP),文獻[1]中作者利用錐上的不動點指數理論獲得了四階周期邊值問題

正解的存在性和多重性.文獻[2]在周期邊界下對四階微分算子L4u=u(4)?βu00+αu在F4={u∈C4[0,1]|u(i)(0)=u(i)(1),i=0,1,2;u(3)(0)≥u(3)(1)}中建立了強極大值原理,并用錐上的不動點指數理論,在α,β∈R滿足條件

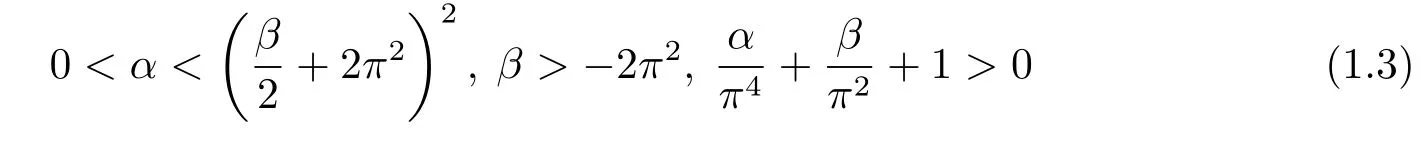
時,獲得了四階周期邊值問題(PBVP)

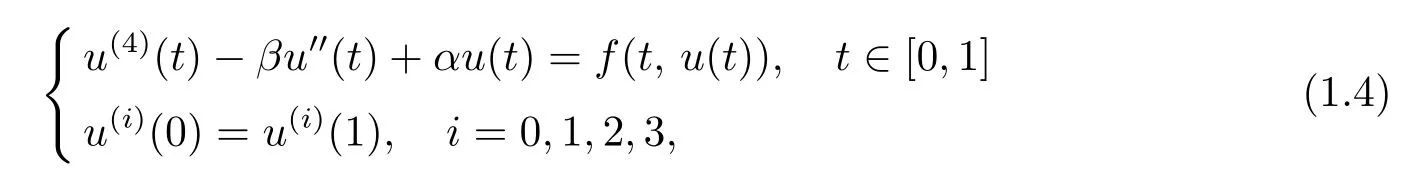
正解的存在性.文獻[3]中作者利用錐上的不動點指數理論獲得了四階變系數周期邊值問題

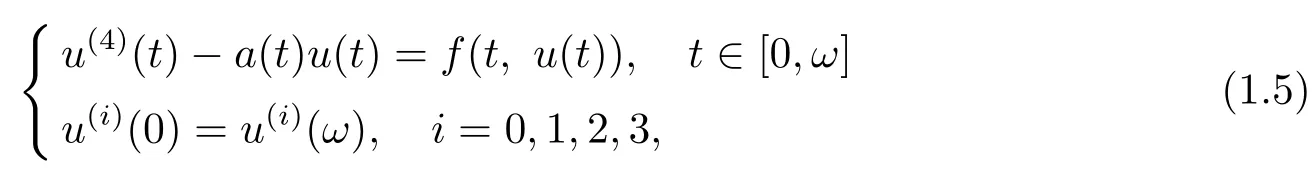
正解的存在性.

對非線性項f含有u00項的四階周期邊值問題(PBVP)

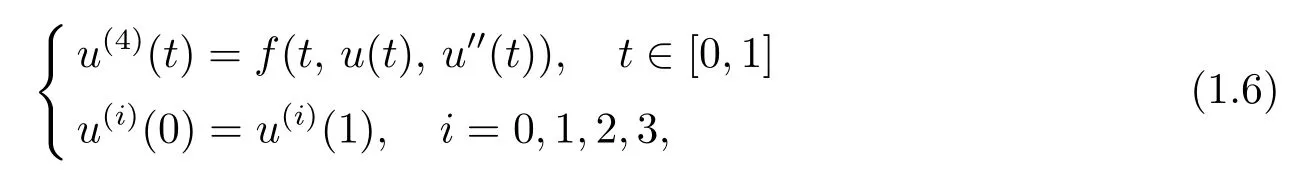
文獻 [12]在上下解存在的情形下,利用Banach壓縮原理,獲得了周期解的存在性與唯一性.文獻 [13]應用單調迭代方法在f(t,u,v)關于u,v滿足單邊Lipschitz條件時,獲得了PBVP(1.6)解的存在性結果.文獻[14]利用建立的新極大值原理和Fredholm抉擇,用上下解方法獲得了PBVP(1.6)解的存在性結果.文獻[16]推廣了文獻[2]中的結果,用錐上的不動點指數理論獲得了四階周期邊值問題(PBVP)

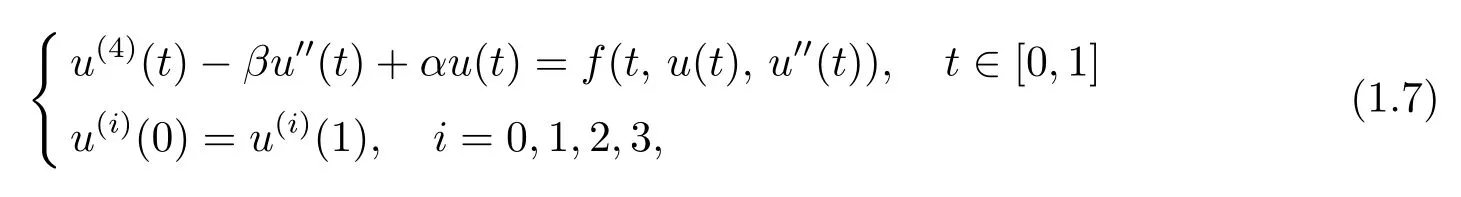
正解的存在性.以上工作討論的均是非線性項f不含未知函數的導數項或僅含二階導數項u00的特殊情形,而在較為復雜的彈性梁模型中,非線性項中可能會出現u0與u000.對非線性項f含有u0,u00,u000的完全四階周期邊值問題(1.1),未見有人研究.本文利用錐上的不動點指數理論,在允許非線性項f(t,x0,x1,x2,x3)關于x0,x1,x2,x3超線性增長的不等式條件下,獲得了四階周期邊值問題(1.1)正解的存在性.

2 預備知識

記I=[0,1],R+=[0,+∞),C(I)表示定義在I上的全體連續(xù)函數按范數構成的Banach空間.

根據文獻[2]中的引理3,微分算子Lu=u(4)(t)?βu00(t)+αu(t)在周期邊界條件下滿足極大值原理,且有下面引理.

3 主要結果