POSITIVE SOLUTIONS AND INFINITELY MANY SOLUTIONS FOR A WEAKLY COUPLED SYSTEM?
Xueliang DUAN (段雪亮)?
School of Mathematical Sciences, Zhejiang University, Hangzhou 310027, China
E-mail : xueliangduan@outlook.com
Gongming WEI (魏公明)
College of Science, University of Shanghai for Science and Technology, Shanghai 200093, China
E-mail : gmweixy@163.com
Haitao YANG (楊海濤)
School of Mathematical Sciences, Zhejiang University, Hangzhou 310027, China
E-mail : htyang@zju.edu.cn

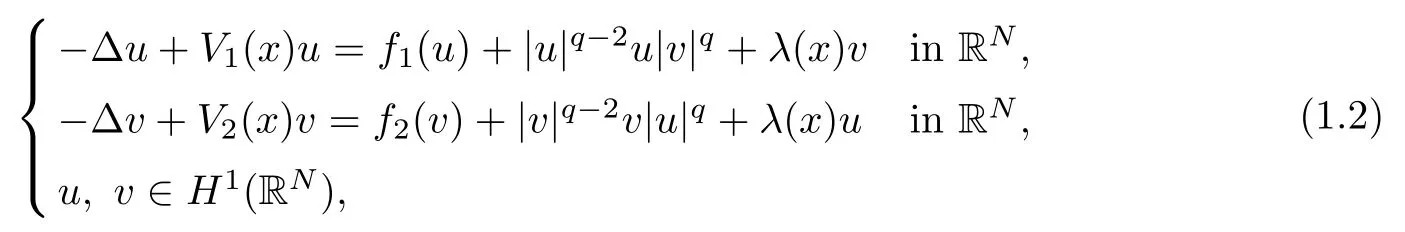
(F1) for fi∈ C1(R) andthere exists a constant c>0 such that
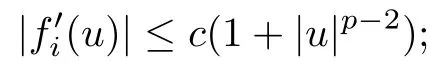
(F2) fi(u)= ?fi(?u) and fi(u)≥ 0 for u ≥ 0;
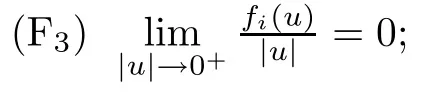
(F4)is non-decreasing on (?∞,0) and (0,+∞);Vi(x),i=1,2, satisfies that:
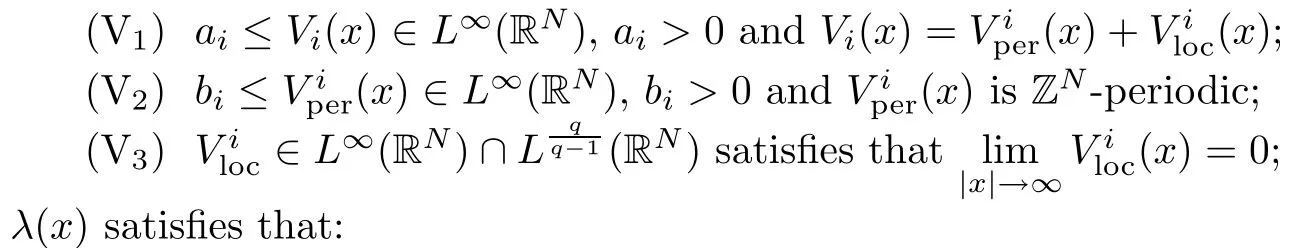
(A) λ(x) ∈ L∞(RN) is ZN-periodic and λ(x) > 0. Moreover, there exists 0 < μ < 1 such that
To get ground state solutions of (1.2), we first consider the following Schrdinger system with periodic potentials:
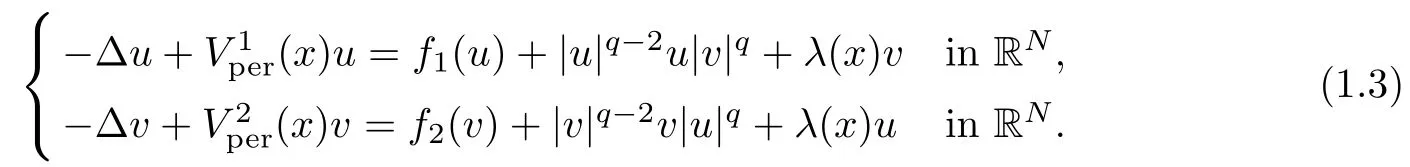
Theorem 1.1Suppose that (F1)–(F4), (A) and (V2) are satisfied. Then
(i) eq.(1.3) has a positive ground state solution (u,v),u,v >0;
(ii) eq.(1.3) admits infinitely many pairs of geometrically distinct solutions.
Solutions ω1,ω2∈ E are geometrically distinct if O(ω1)∩ O(ω2) = ?, where O(u,v) :={(u(·? z),v(·? z)):z ∈ ZN} is the orbit of (u,v)∈ E under the action of (ZN,+). If (u,v) is a solution, then the whole orbit O(u,v) consists of solutions.
From conditions(V1)–(V3),we know that(1.2)is close-to-periodic,i.e.,has potential functions Vi(x) from the sum of ZN-periodic and vanishing functions. Under the cases that eitherthe translation of energy functional is not invariant, which implies that we cannot directly prove that the weak limit of the minimizing sequence is nontrivial. Here the problem is addressed by energy estimates and a concentration compactness argument.
Theorem 1.2Suppose that (F1)–(F4), (A) and (V1)–(V3) are satisfied. Moreover, if=1,2 satisfies that
We also study the nonexistence of the ground state solution of (1.2). By altering the assumptions of=1,2, we obtain the nonexistence result by energy estimates.
Theorem 1.3Suppose that (F1)–(F4), (A) and (V1)–(V3) are satisfied. Moreover, if=1,2 satisfies that
The paper is organized as follows: in Section 2 we present some technical results. We introduce the PS sequence on a Nehari manifold in Section 3. In the final section we prove Theorems 1.1–1.3.
2 Preliminaries
We first state certain basic notations used in this paper. The first is the Hilbert space
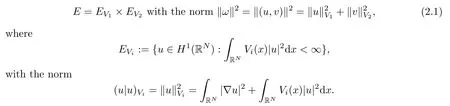
Obviously,EViis equivalent to the standard H1(RN). We denote|·|pas the norm of Lp(RN)andas the norm of the vector in Lp(RN)×Lp(RN). It is a classical argument that weak solutions of (1.2) are critical points of the functional J(ω)=J(u,v):E → R,
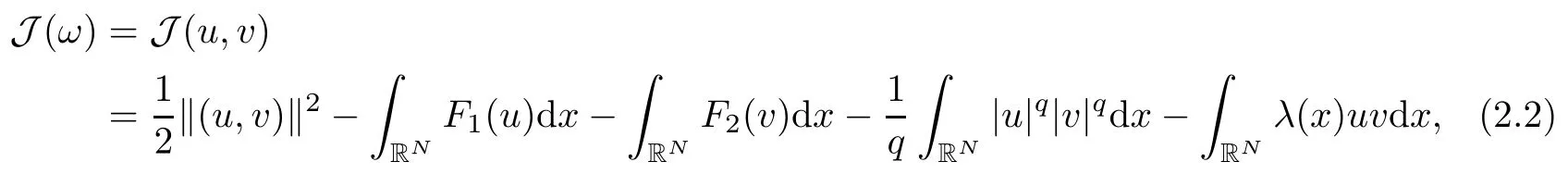
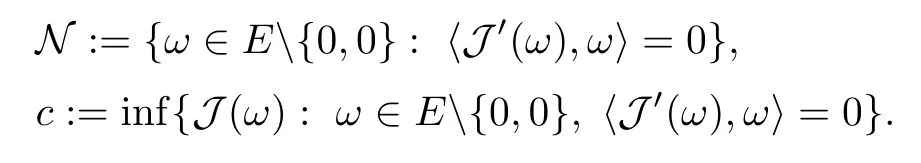
Jper, Nperand cperof (1.3) are well-defined in a similar way. From conditions (V1)–(V3), we deduce that
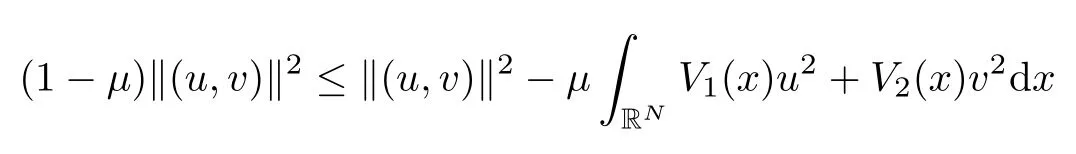
In what follows we provide several lemmas for our proof.
Lemma 2.1Suppose that (F1)–(F4) hold. Then
(i) Fi(u)=Fi(?u)≥ 0;
(ii) fi(u)u ? 2qFi(u)≥ 0;
(iii) For any ε>0, there exists Cε>0 such that |fi(u)u|+|Fi(u)|≤ ε|u|2+Cε|u|p;
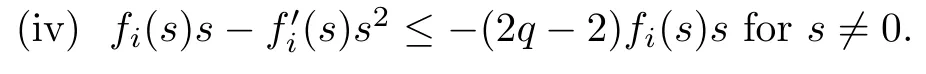
Proof(i) In view of (F2), for u ≥0 we have that
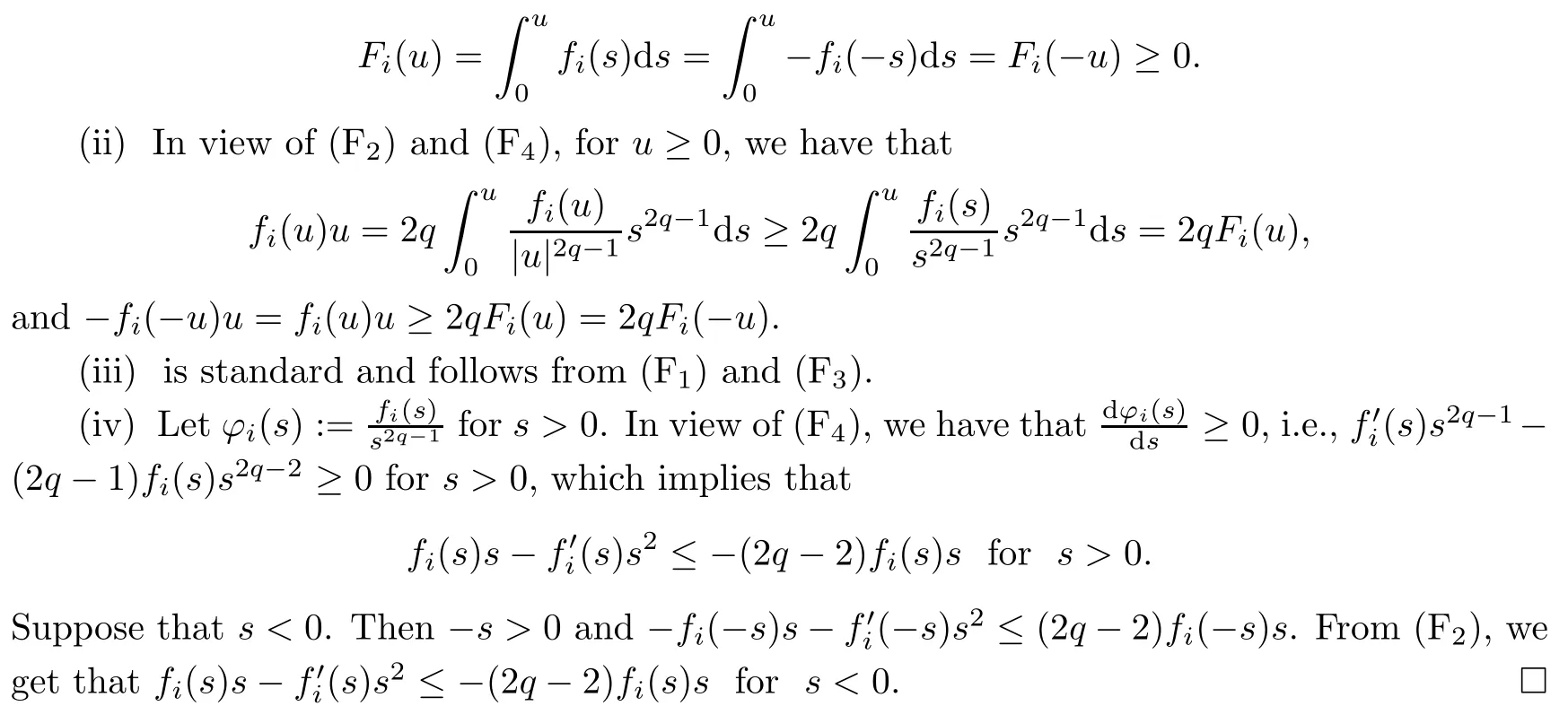
Lemma 2.2Suppose that (F1)–(F4), (A) and (V1)–(V3) are satisfied. Then there exists ρ >0 such that
ProofSuppose, by contradiction, that (ωn) ? N is a sequence such thatas n → +∞. From (2.3), we find that
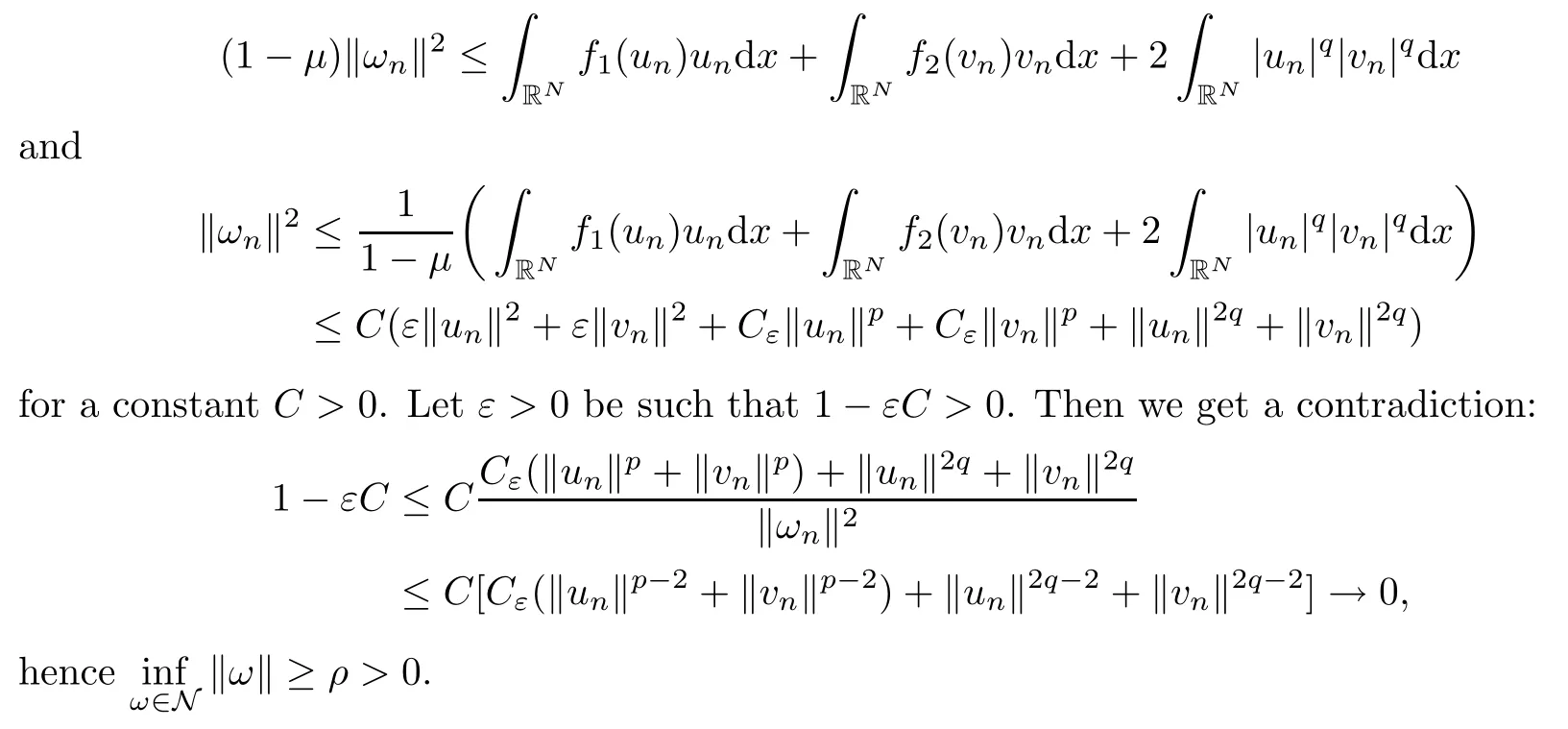
Lemma 2.3Suppose that (F1)–(F4), (A) and (V1)–(V3) are satisfied. Then, for every ω ∈ E{0,0},there is a unique number t>0 such that tω ∈ N and J(tu,tv)=
ProofFor any (u,v)∈E{(0,0)} and t>0, let
We have ?(t) ≥ Ct2for a small t > 0. On the other hand, we have ?(0) = 0 and ?(t) → ?∞as t → +∞. Hence there is a maximum point tmaxofMoreover, we have that ?′(tmax)=J′(tmaxω)ω =0 and tmaxω ∈ N.
We check that the number t is unique. For any ω ∈ N, it follows from Lemma 2.2 that
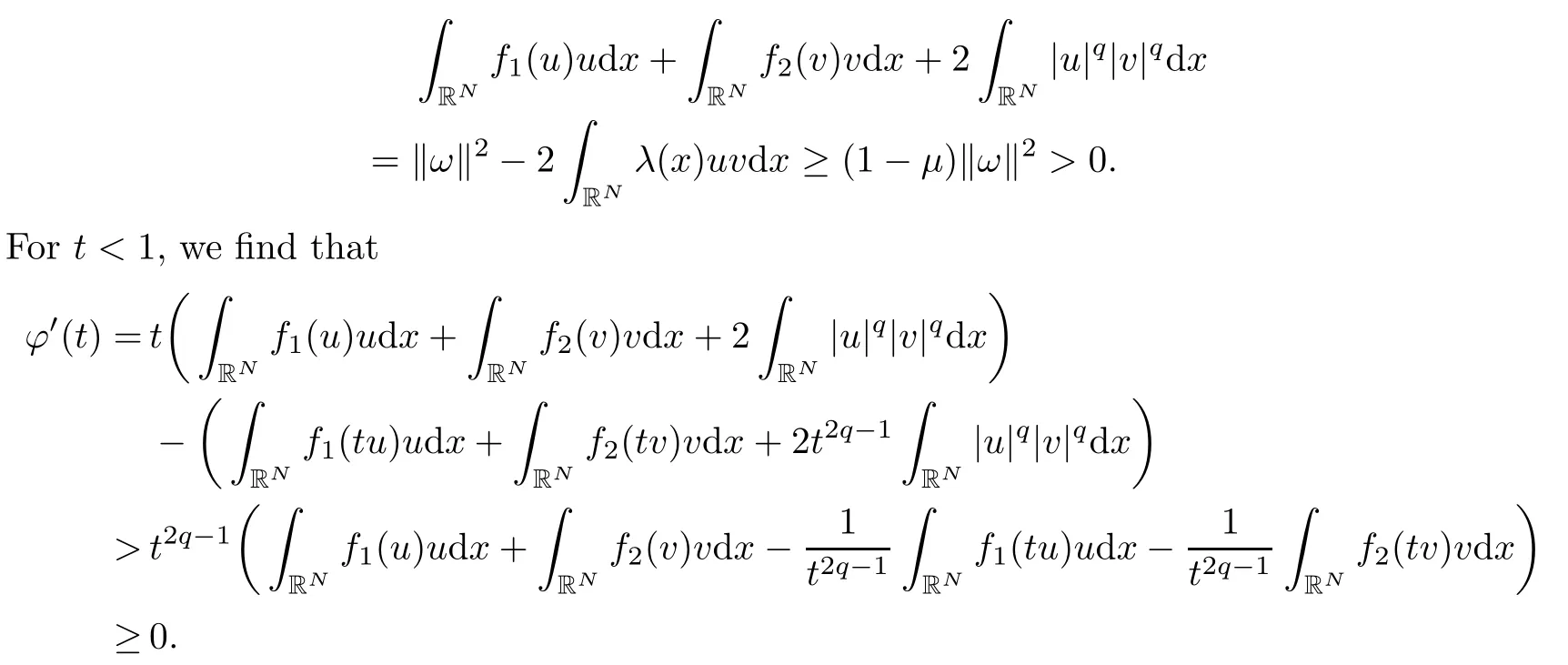
For t > 1, we have that ?′(t) < 0. Hence ?(t) < ?(1) for t ∈ (0,+∞){1}. ?(1) is the unique maximum of ?(t).
The properties of N are stated below.
Proposition 2.4(i) N is a complete metric space;
(ii) N ?E is a C1-manifold;
(iii) J|Nis bounded from below by a positive constant;
(iv) ω is a nonzero free critical point of J if and only if ω is a critical point of J constrained on N.
Proof(i) Let (ωn) ? N be a sequence such thatas n → +∞. By the embedding theorem, we have|un? u0|r→ 0 and |vn? v0|r→ 0 for 2 ≤ r <2?. It is clear that
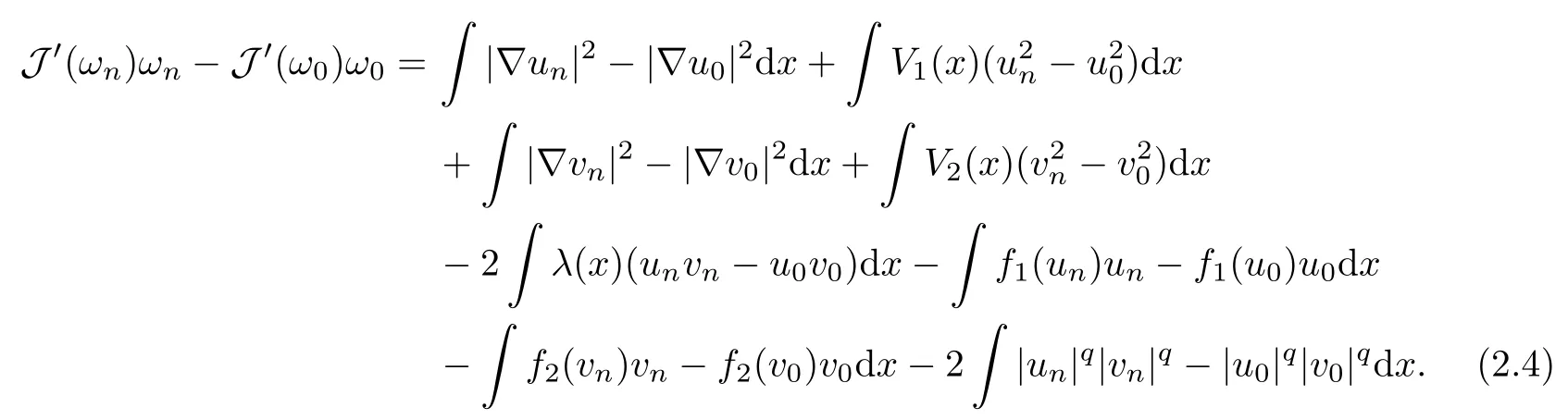
Since |un? u0|2→ 0, applying Hlder’s inequality, we get that

Similarly, 2 λ(x)(un? u0)v0dx → 0. It follows that
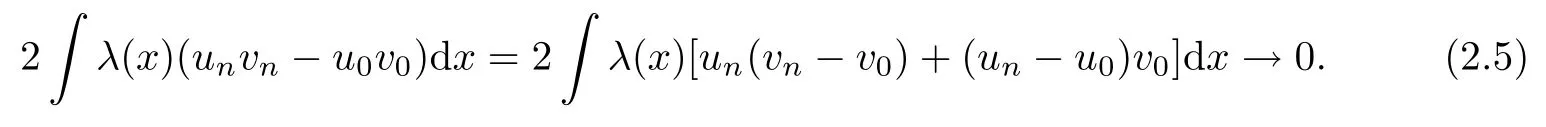
In view of [3, Theorem 4.9], since un→ u0in Lr(RN) for 2 ≤ r < 2?, up to a subsequence,there exist l(x)∈L2(RN) and m(x)∈Lp(RN)such that |un(x)|≤l(x) and |un(x)|≤m(x) for a.e. x ∈RN. We then have that
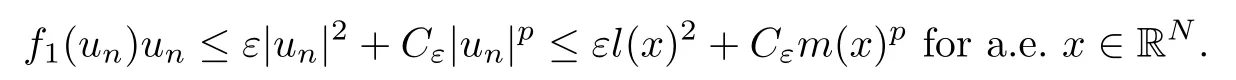
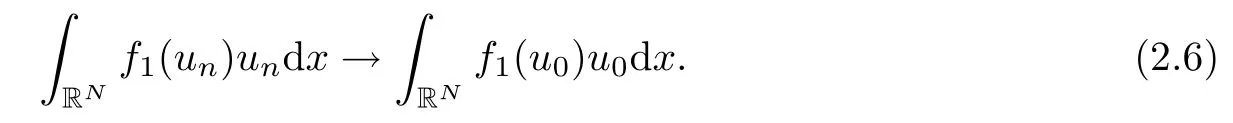
Since un→ u0and vn→ v0in L2q(RN), up to a subsequence,there exist h(x),g(x)∈ L2q(RN)such that |un|≤ h(x) and |vn|≤ g(x) for a.e. x ∈ RN. Then
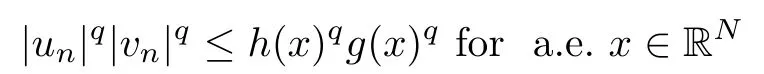
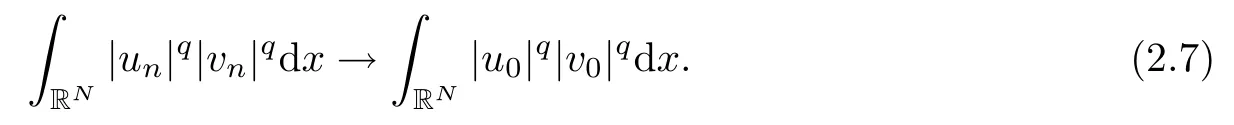
Combining (2.4), (2.5), (2.6) and (2.7), we get
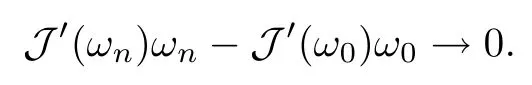
Since J′(ωn)ωn=0, J′(ω0)ω0=0. Using Lemma 2.2 andHence ω0∈ N, and N is a complete metric space.
(ii) For any ω ∈ N, let
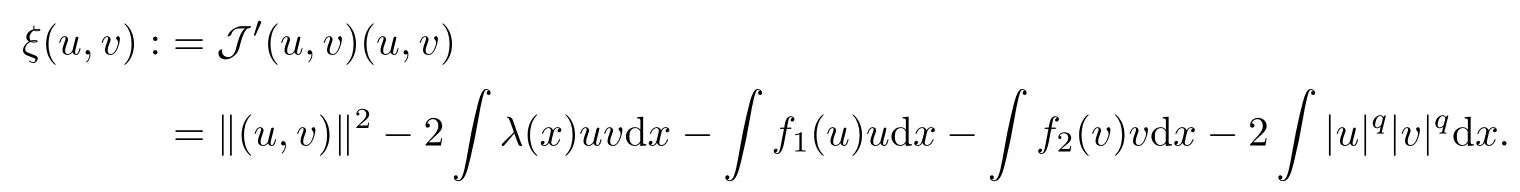
From (iv) of Lemma 2.1, we deduce that
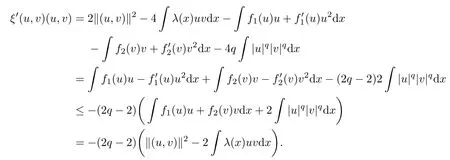
In view of Lemma 2.2, we have that
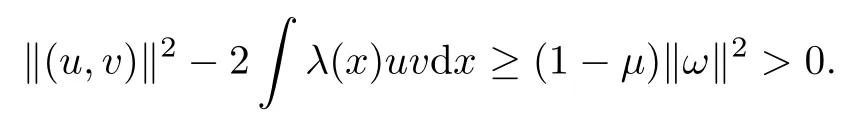

and N ?E is a C1-manifold.
(iii) In view of (ii) of Lemma 2.1 and Lemma 2.2, for ω ∈ N we have that
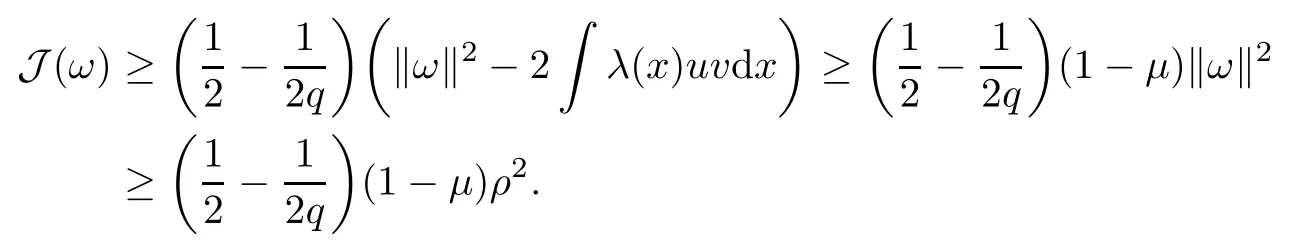
3 Palais-Smale Sequence on Nehari Manifold
In this section,suppose that(F1)–(F4),(A)and(V1)–(V3)are satisfied. We find a bounded Palais-Smale sequence on a Nehari manifold in the following lemma:
Lemma 3.1There exists a bounded sequence(un,vn)?N such that J(un,vn)→c and J′(un,vn)→ 0 as n → +∞.
ProofFrom Proposition 2.4, we get that J is bounded from below on N. By applying Ekeland’s variational principle [21], one obtains a sequence (un,vn)? N satisfying
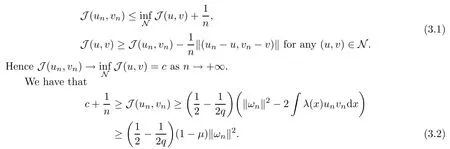
From (3.2), there exists C >0 such that

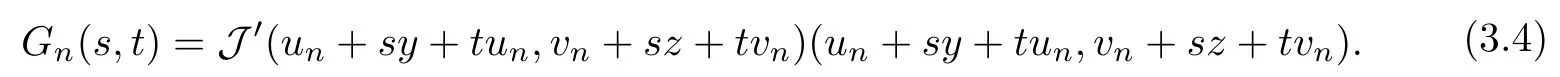
Obviously, Gn(0,0)=J′(un,vn)(un,vn)=0. From (2.8), we get that
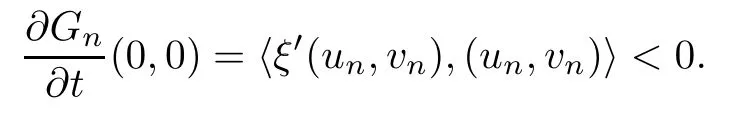
By using the implicit function theorem, there exists a C1function tn(s) : (?δn,δn) → R such that tn(0)=0 and
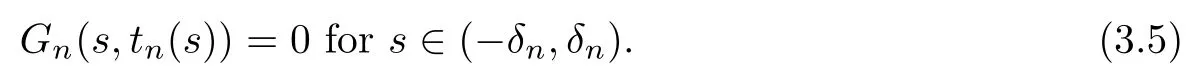
Differentiating Gn(s,tn(s)) in s at s=0, we get that
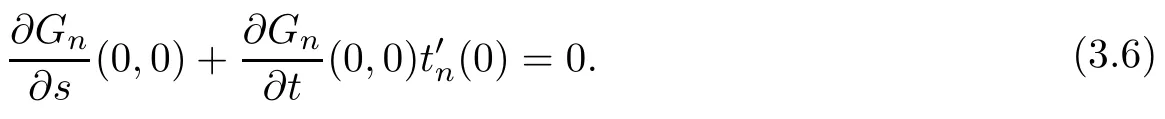
From Lemma 2.2 and (2.8), we find that
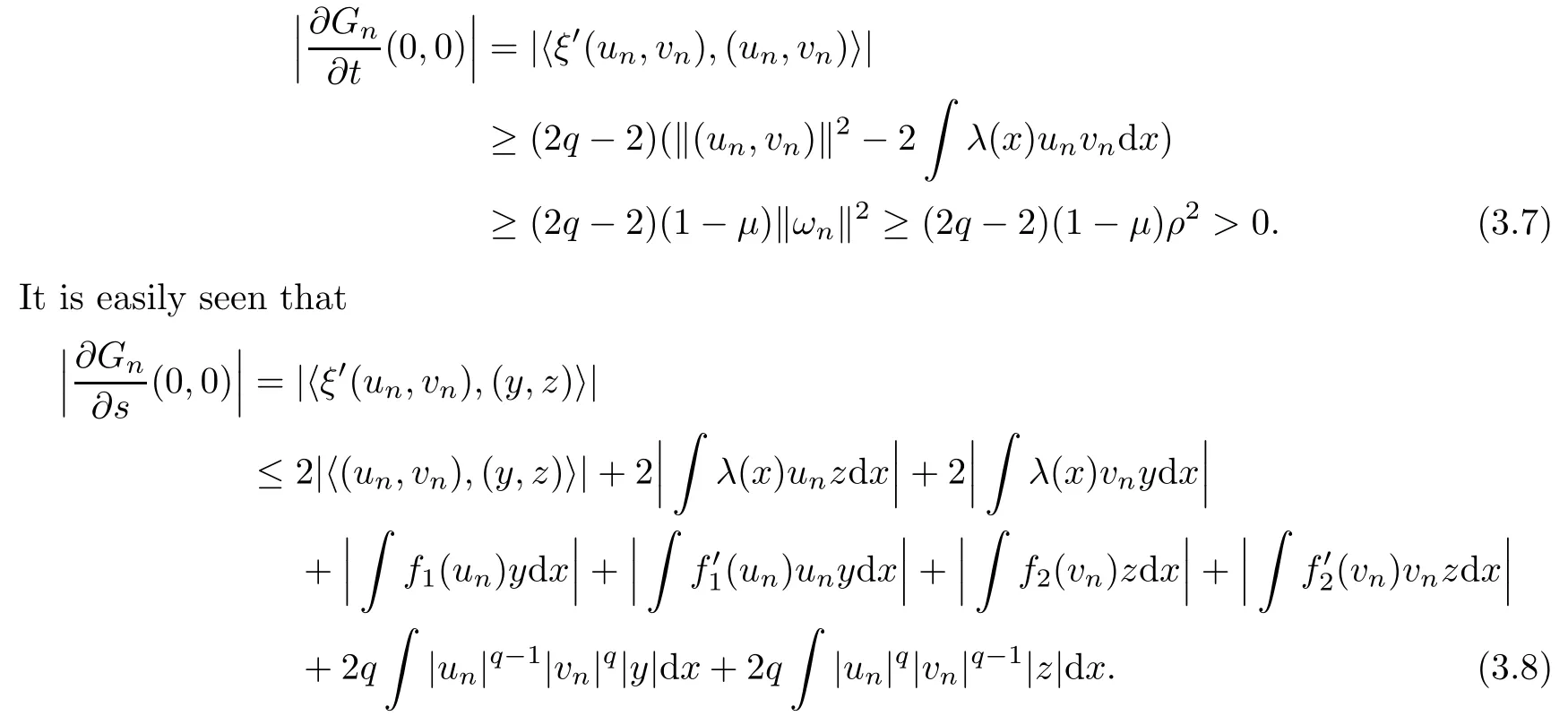
In view of (3.3), applying Hlder’s inequality and an embedding theorem, we deduce that
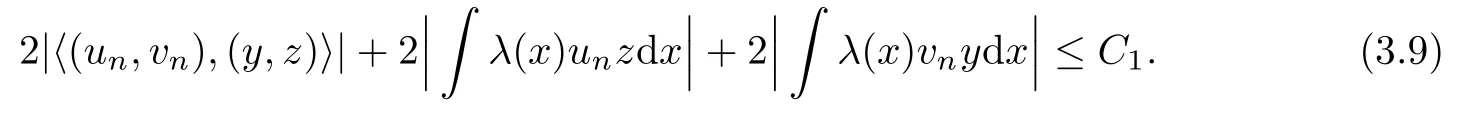
Combining (F1), (iii) of Lemma 2.1 and (3.3), we find that
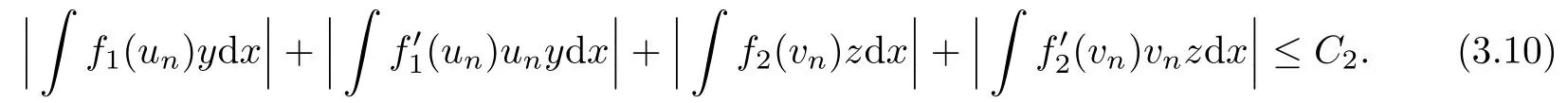
Moreover, we have that
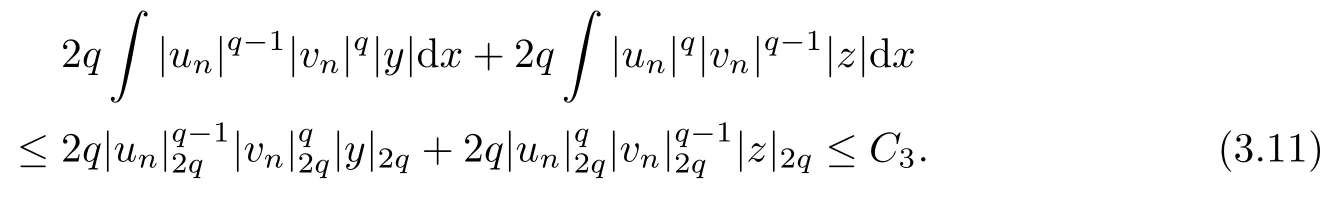
From (3.8)–(3.11), we get that

Combining (3.6), (3.7) and (3.12), we find that

From (3.4) and (3.5), we know that (y,z)n,s∈ N for s ∈ (?δn,δn). In view of (3.1), we have
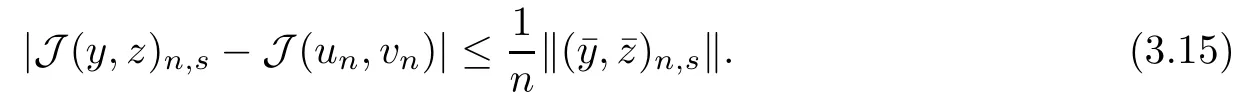
Applying a Taylor expansion on the left side of (3.15), we have that
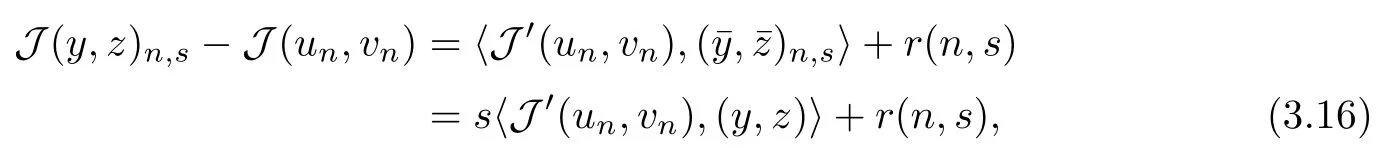

where C6is independent of n. It follows from(3.17)that r(n,s)=o(|s|)as|s|→0. Combining(3.15), (3.16) and (3.17), we find that

Hence J′(un,vn)→ 0 as n → +∞.
From Lemma 3.1, we find a bounded PS sequence (ωn)? N such that J(un,vn)→ c and J′(un,vn)→0. Up to a subsequence, there exists (u0,v0)∈E such that (un,vn)?(u0,v0).
Lemma 3.2Suppose that (un,vn) ? (u0,v0) in E and that J′(un,vn) → 0. Then J′(u0,v0)=0.
ProofFor any φ =(?,ψ), ?, ψwe have that
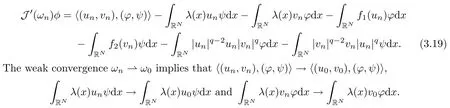
Let K ? RNbe a compact set containing supports of ?,ψ, up to a subsequence, so we have
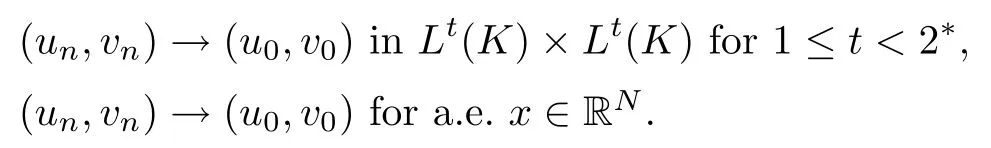
In view of [3, Theorem 4.9], there exist lK(x) and mK(x)∈L2q(K) such that
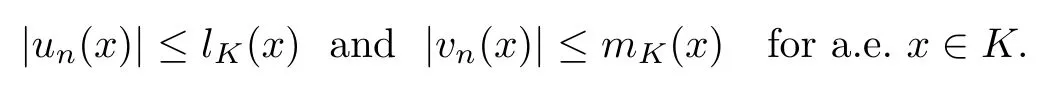
Let hK(x):=lK(x)+mK(x) for x ∈ K. It is easily seen that hK(x)∈ L2q(K) and that
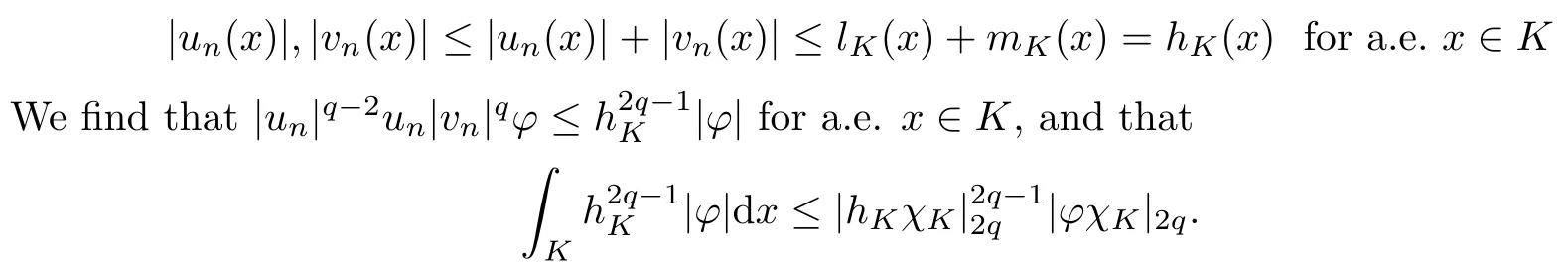
Applying Lebesgue’s dominated convergence theorem, we get
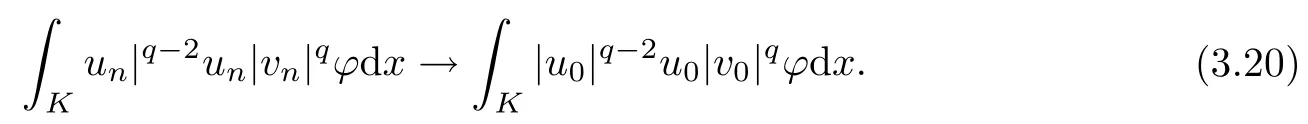
Similarly, there exist rK(x) ∈ L2(K) and gK(x) ∈ Lp(K) such that |un| ≤ rK(x) and |un| ≤gK(x) for a.e. x ∈K. We have that
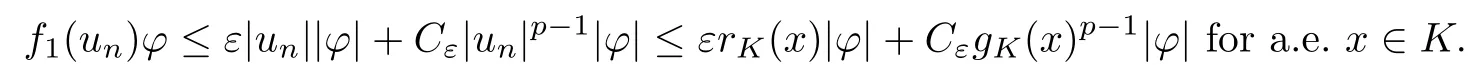
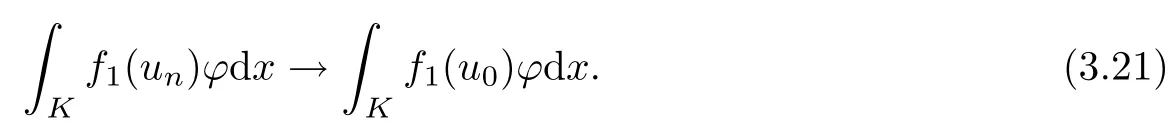
Combining (3.19), (3.20) and (3.21), we get
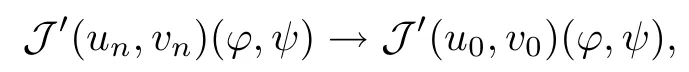
and that J′(u0,v0)=0; i.e., that (u0,v0) is a critical point of J.
Lemma 3.3([21, Lemma 1.21]) If {un} is bounded in H1(RN) and
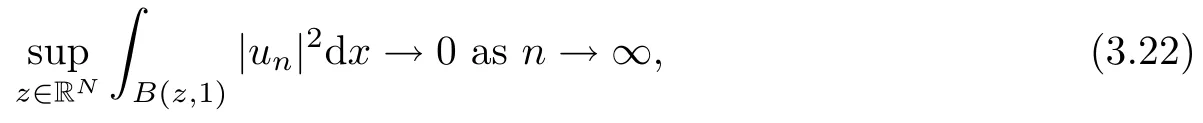
then un→ 0 in Lt(RN) for 2 Lemma 3.4Assume that {ωn} is a PS sequence constrained on N, which satisfies ProofWe have From Lemma 3.3, we deduce that un,vn→ 0 in Lr(RN) for 2 < r < 2?. Letting ε → 0, we have that We prove Theorems 1.1–1.3 in Subsections 4.1–4.3. We note,in particular,that all lemmas in Sections 2–3 hold in the case ExistenceFrom Lemma 3.1,we find a bounded PS sequence(ωn)of Jper;i.e.,a sequence ωn?Npersuch that Jper(ωn) →cperand→0. Applying Lemma 3.2, up to a subsequence, we have In view of Lemma 3.4, we haveThis contradicts Lemma 2.2. In view of Lions’Lemma [10], there exists (yn)?RNsuch that We assume, without loss of generality, that Since Jperand Nperare invariant under translations of the formwith k ∈ ZN,we may assume that (zn) is bounded in ZN. Since un→u0inwe have that(u0,v0)∈ Nperand Jper(u0,v0)≥ cper. Applying Fatou’s lemma, we have that Hence Jper(u0,v0)=cperandis a ground state solution of (1.3). We have (|u0|,|v0|) ∈ E. There exists t > 0 such that (t|u0|,t|v0|) ∈ Nperand Jper(t|u0|,t|v0|)≥cper. It is clear that Hence (u′,v′):=(t|u0|,t|v0|), u′,v′≥ 0 is a nonnegative ground state solution of (1.3). We now observe(1.3). If u′=0,then v′=0. This stands in contradiction to(u′,v′)∈ Nper.We getApplying the strong maximum principle to each equality of (1.3),we get u′> 0 and v′> 0, and ω′= (u′,v′) is a positive ground state solution of (1.3). This completes the proof of (i) of Theorem 1.1. Multiple SolutionsWe follow the arguments of[2,16]. Let(u,v)∈E{0,0},and S1:=There is a unique number t(u,v)> 0 such that t(u,v)(u,v) ∈ Nper.We denote m:S1→Nperby m(u,v)=t(u,v)(u,v), and the inverse function is Let τkdenote the action of (ZN,+) on E; i.e., τk(u,v) := (u(·? k),v(·? k)), where k ∈ ZN.We introduce several lemmas before our proof. Lemma 4.1([2, Lemma 6.1]) The function m : S1→Nperis a local diffeomorphism of class C1. Lemma 4.2([2, Lemma 6.2]) The function m?1: Nper→ S1is Lipschitz continuous;i.e., for ω1,ω2∈ Nper, it holds that where ρ>0 is given by Lemma 2.2. and let F ? L be a symmetric set such that for every orbit O(α,β), there is a unique representative β ∈ F. We assume that F is finite. By [16, Lemma 2.13], we have that Hence L is a discrete set. Lemma 4.3Let d ≥ cper=infNperJper. Ifi =1,2 are two Palais-Smale sequences for Jper? m such that where the constant ρ(d)>0 depends only on d, but not on the particular choice of sequences. ProofLeti = 1,2. In a fashion similar to [16, Corollary 2.10],= 1,2 are Palais-Smale sequences of Jper. Since Jperis coercive on Nper, the sequences are bounded in E. We get, by the Sobolev embedding theorem, that= 1,2 are bounded in Lr(RN) for 2 ≤ r ≤ 2?. Here we consider two cases. In view of Lemma 3.3, for 2 For ε >0, there exists Cε>0 such that For constants C0and Dε>0, it holds that In view of (4.3), we get that Case 2In view of Lions’ lemma [10], there exists a sequence (yn) ? RNsuch that where β is defined as Lemma 2.2. If (u1,v1) =(u2,v2)=(0,0), we have that This completes the proof of Lemma 4.3. By[15,Lemma II.3.9]and Lemma 4.2,we have that Jper?m → R admits a pseudo-gradient vector field. In view of Lemma 4.3, we can repeat the arguments of [2, Theorem 1.4]and [16,Theorem 1.2]. For any k ≥ 1, there exists (αk,βk)∈ S1such that and γ is a Krasnoselskii genus for closed and symmetric sets. Since ck We need the following lemma: ProofIn view of Theorem 1.1, we choose a positive ground state solution (u,v),u,v >0 of Jper. Let t>0 be such that t(u,v)∈N. Then From Lemma 3.1, we find a bounded PS-sequence (ωn) of J; i.e., a sequence ωn? N such that J(ωn)→ c and J′(ωn)→ 0. In view of Lemma 3.2, up to a subsequence, we have Suppose that In view of Lemma 3.4, we haveThis contradicts Lemma 2.2. Similarly, from the proof of Theorem 1.1, there exists a sequence (yn)?RNsuch that For each yn∈ RN, we find zn∈ ZNsuch that We claim that (zn) is bounded. Assuming the claim, we have thatby un→ u0inand hence (u0,v0)∈N and J(u0,v0)≥c. We check the claim. Assume that(zn) is unbounded. We can choose a subsequence of(zn)such that |zn|→∞as n →∞. LetandWe denote K ?RNas a compact set containing supports of ?,ψ, up to a subsequence, so It follows from (4.6) that In view of Lemma 4.4, we get a contradiction. Hence (zn) is bounded. Finally, applying Fatou’s lemma, we have that Let t>0 be such that (t|u0|,t|v0|)∈N. Then J(t|u0|,t|v0|)≥c and Hence (u′,v′):=(t|u0|,t|v0|), u′,v′≥ 0 is a nonnegative ground state solution of (1.2). In view of (1.2), if u′=0,then v′=0. This stands in contradiction to(u′,v′)∈ N. We getApplying the strong maximum principle, we have that u′> 0 and v′> 0,and hence ω′=(u′,v′) is a positive ground state solution of (1.2). Suppose, by contradiction, that there is a ground state solution(1.2). In a fashion similar to the arguments in Theorem 1.2, we find a positive ground state solution ω′=(u′,v′),u′,v′>0 of (1.2). Lemma 4.5Suppose that ProofLet ω′= (u′,v′) (u′,v′> 0) be a positive ground state solution of (1.2). There exists t>0 such that t(u′,v′) ∈ Nper, so Let ω ∈Nperbe a ground state solution of Jper, i.e., Jper(u,v) = cperandWe denote:= ω(·?y) for y ∈ZN, and obviously,∈Nper. Then there exists t > 0 such that tˉω ∈N. For any y ∈ZN, we have that where ε is arbitrary. Letting ε → 0, we get that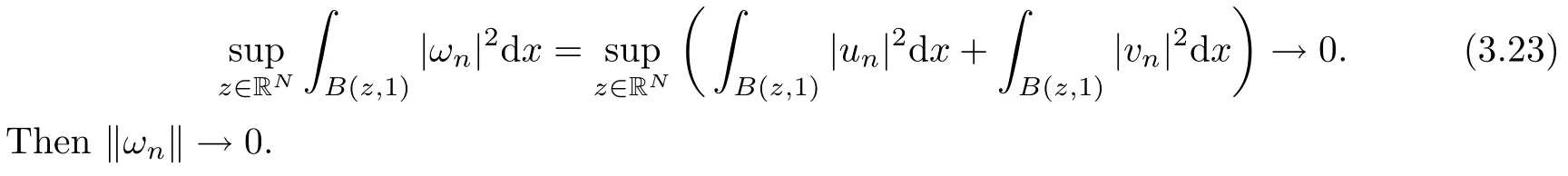
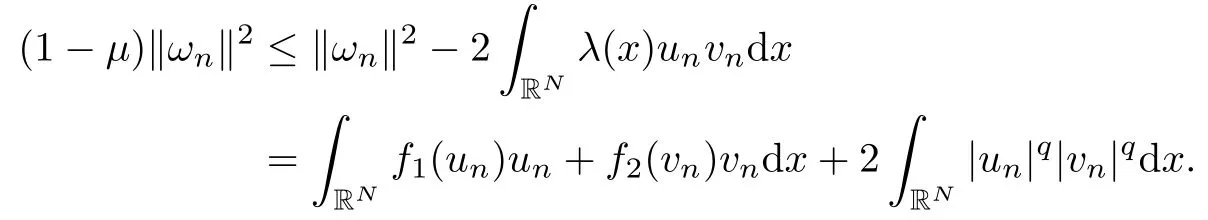
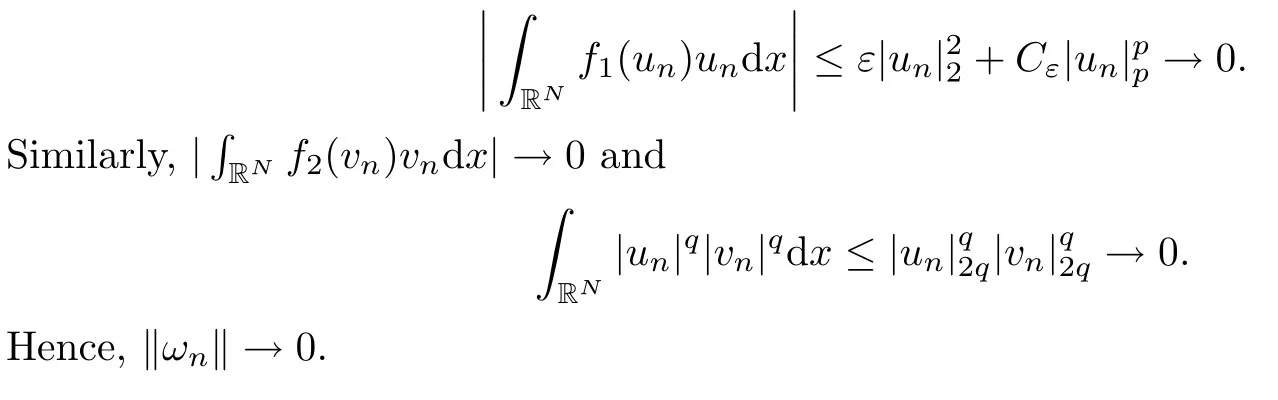
4 Proof of Main Results
4.1 Proof of Theorem 1.1

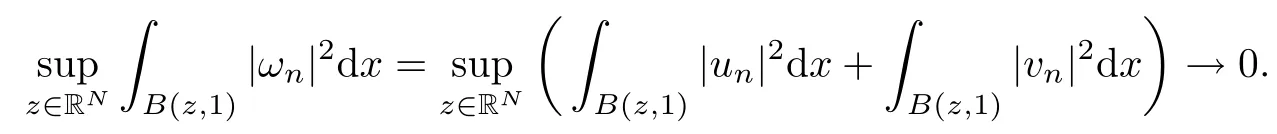
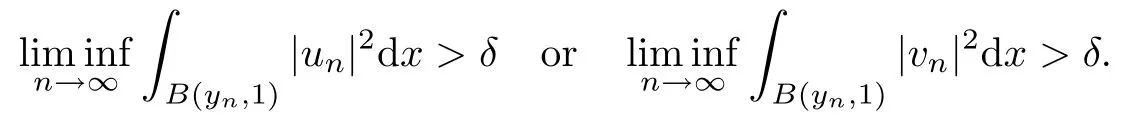
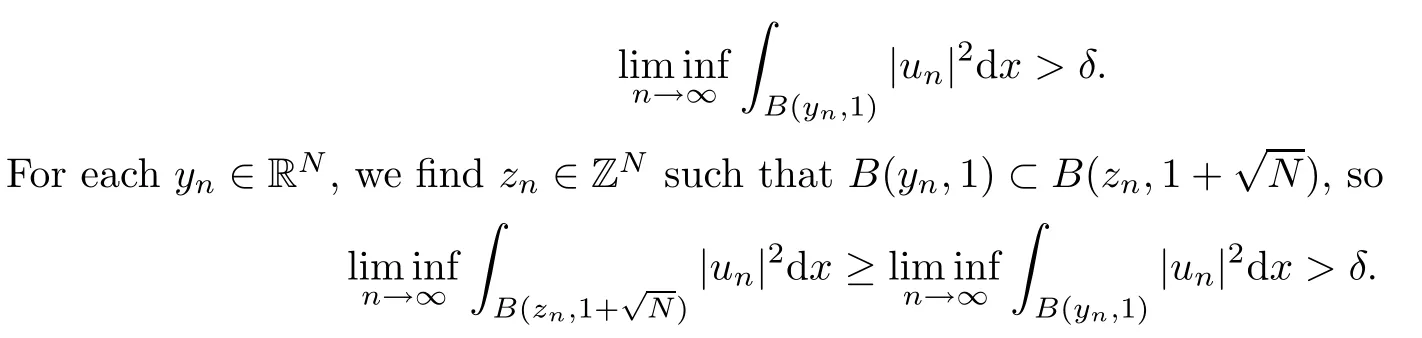
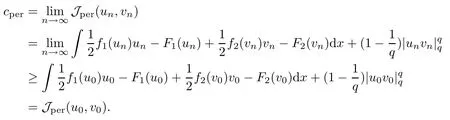
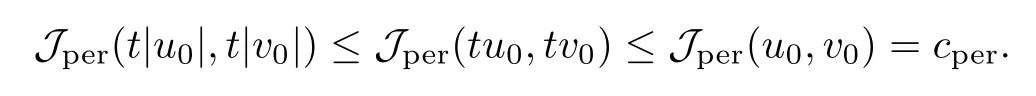
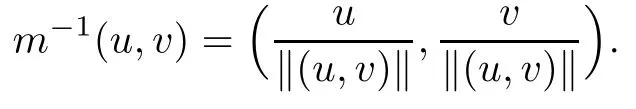
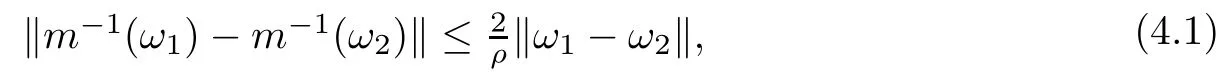
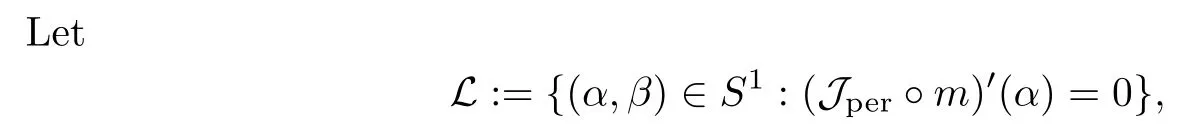
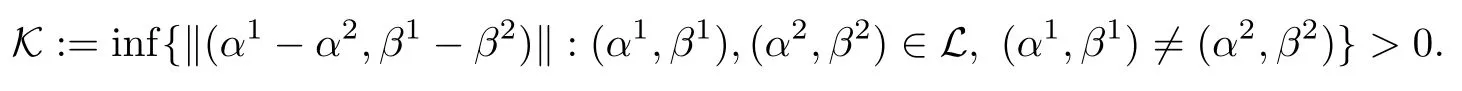
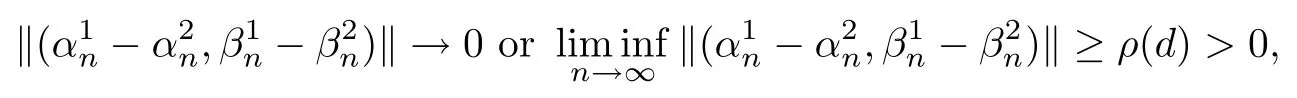
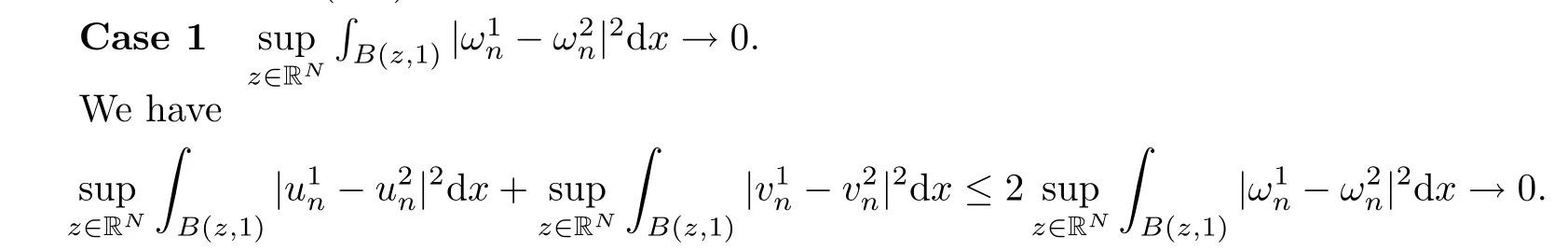

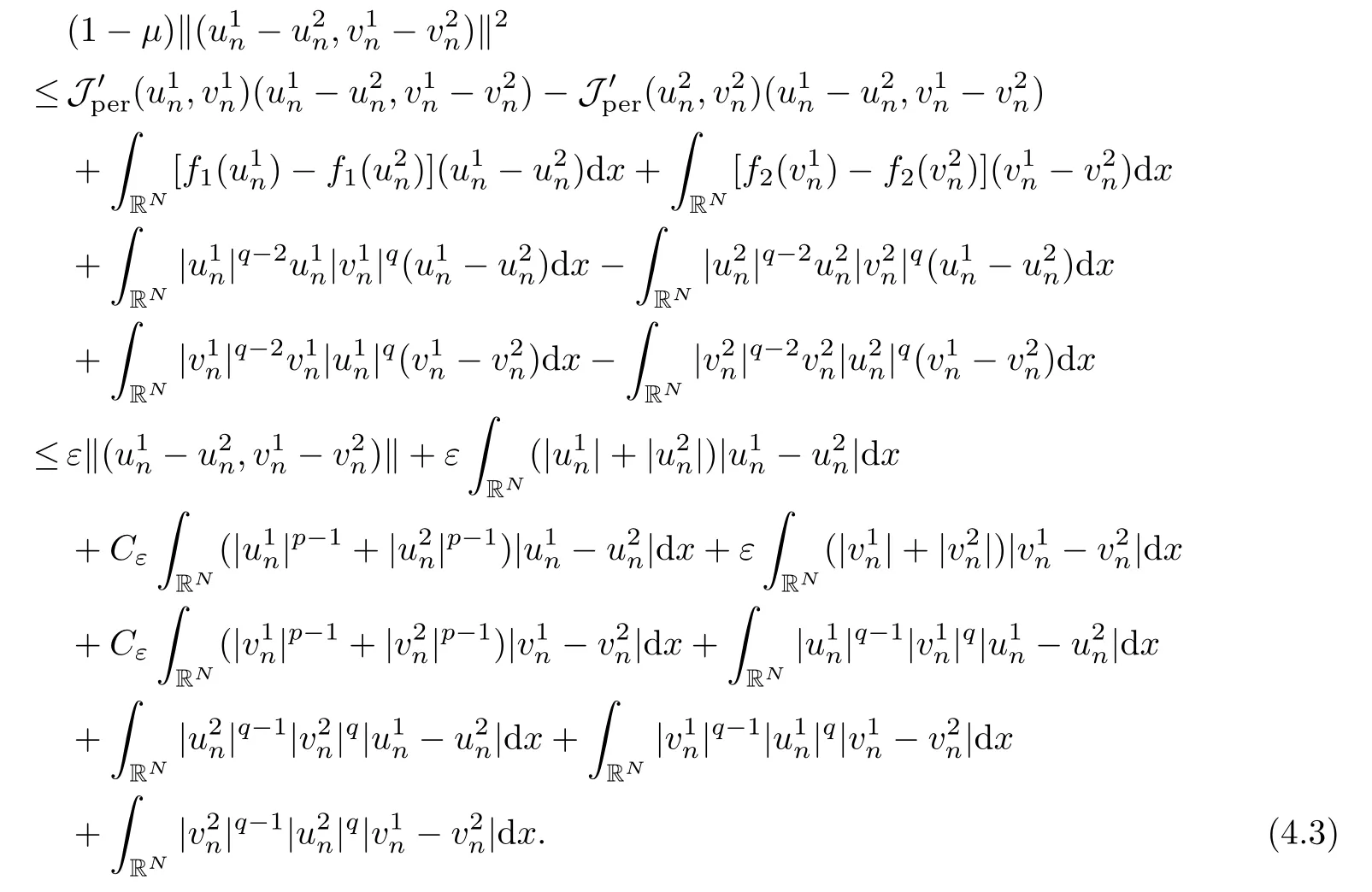
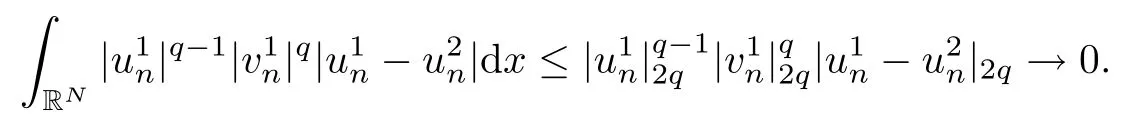
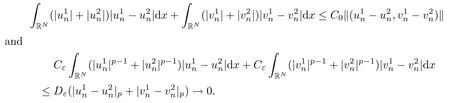
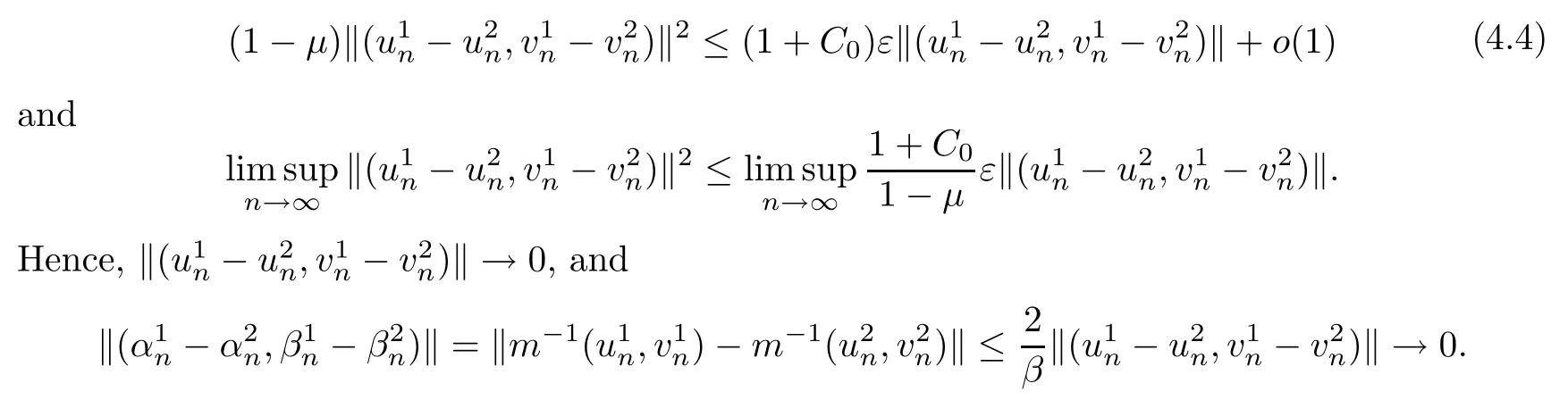
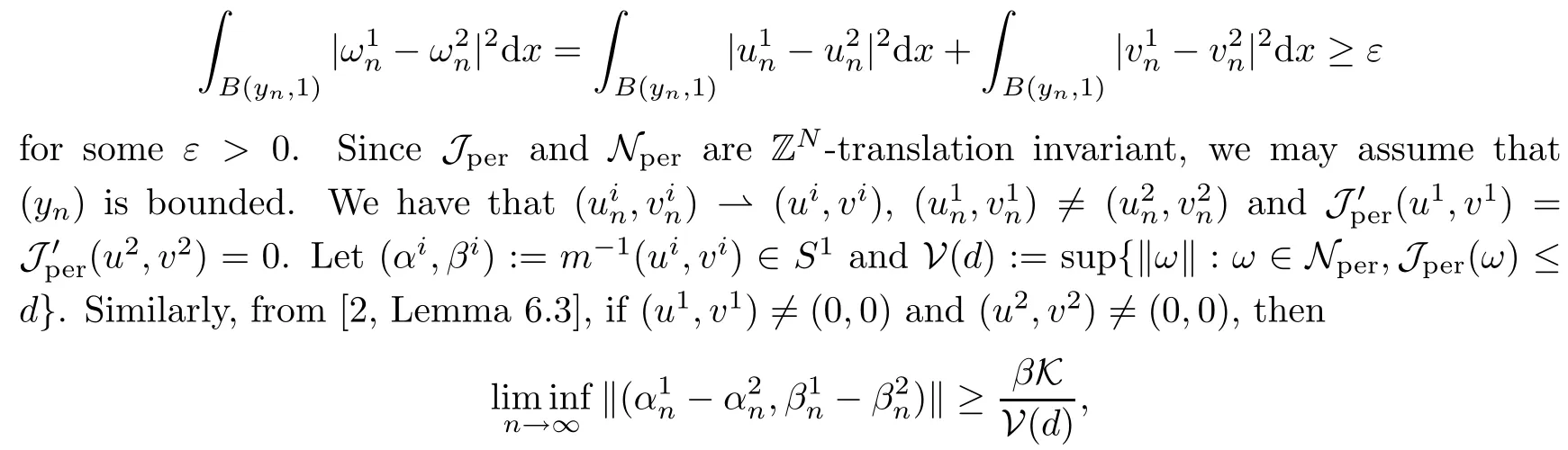
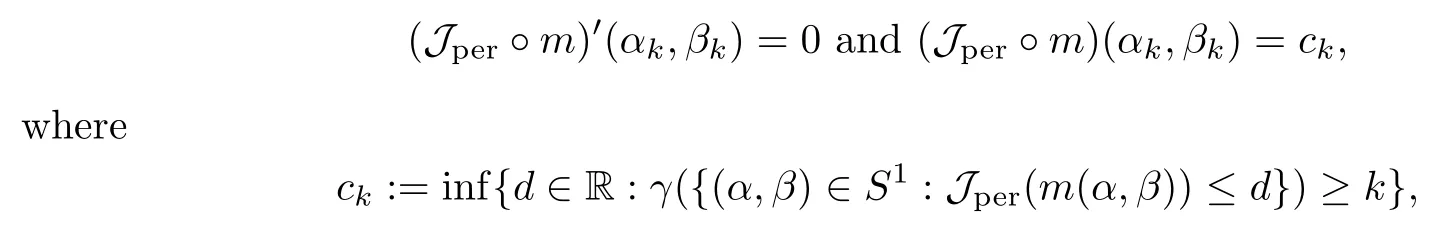
4.2 Proof of Theorem 1.2
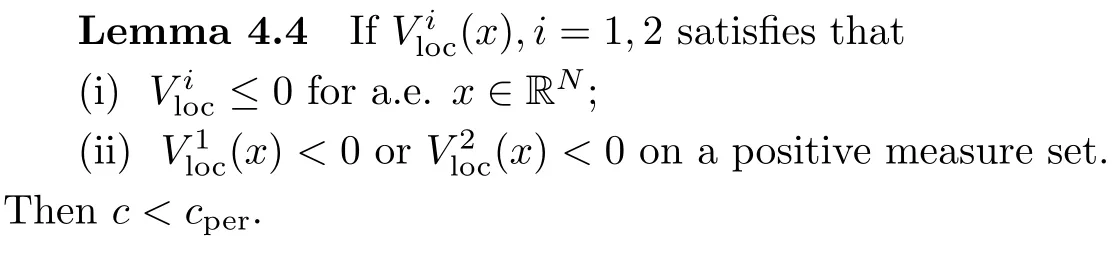
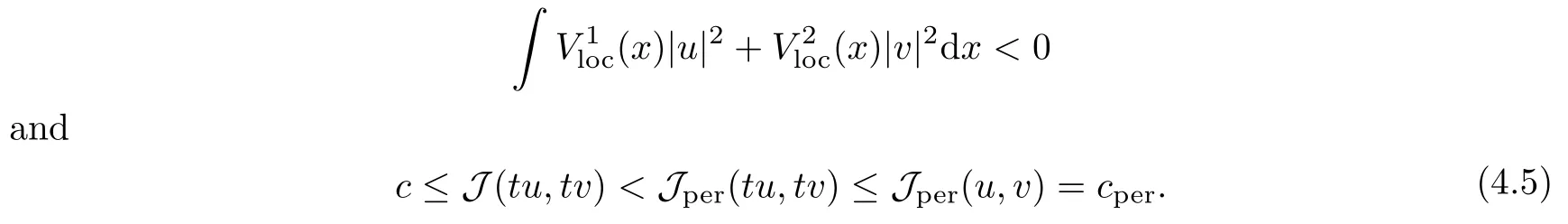
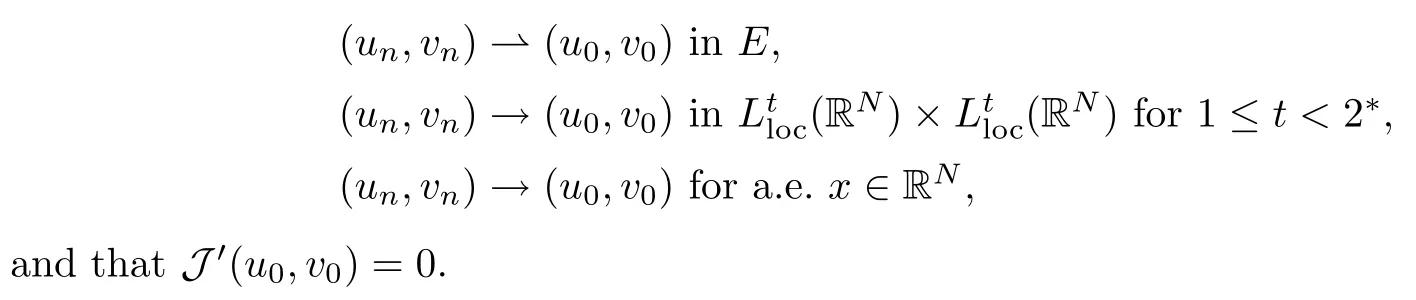
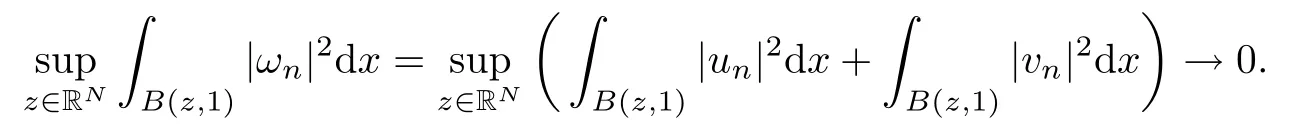
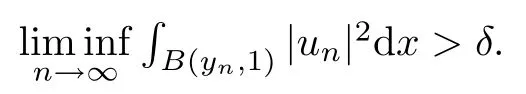
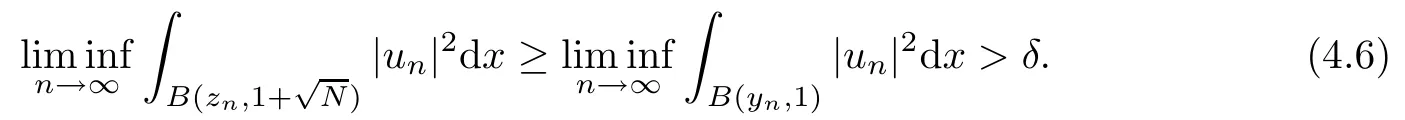
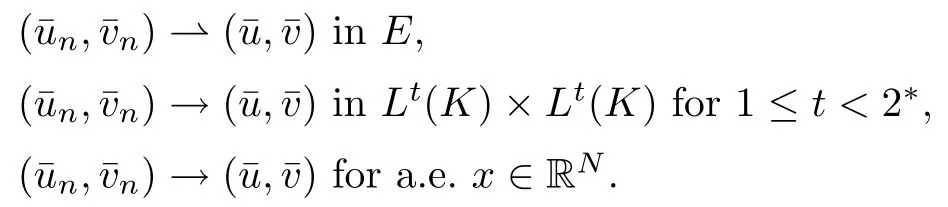
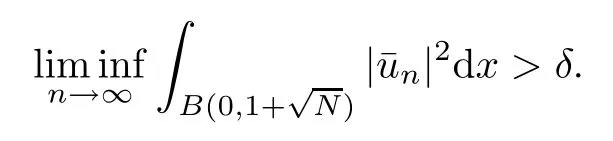

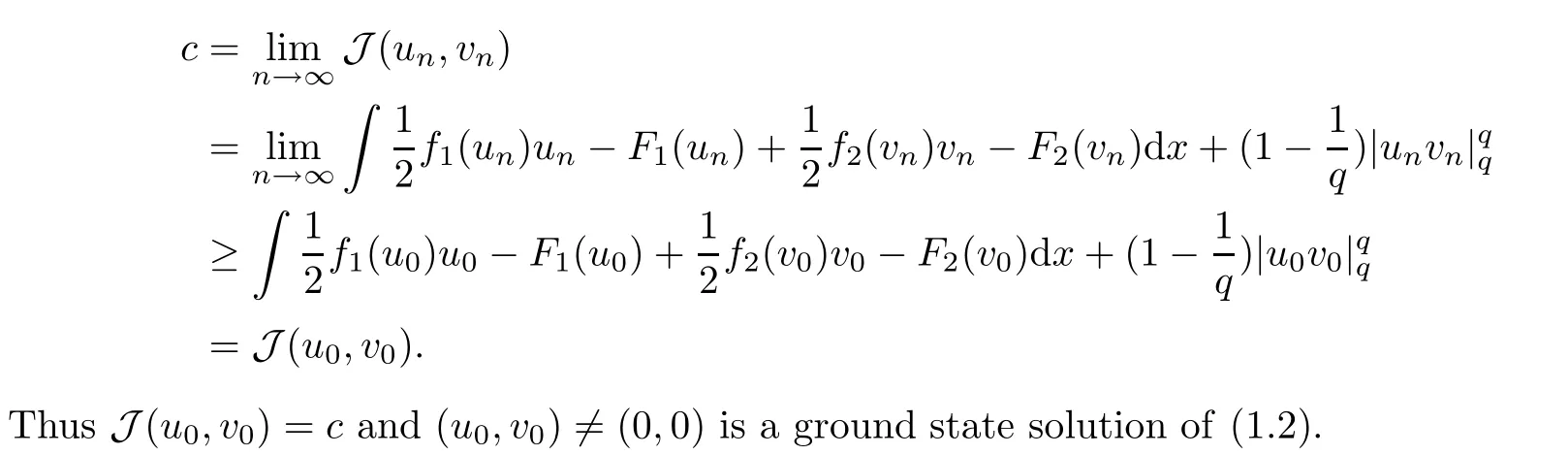
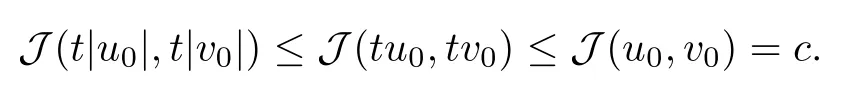
4.3 Proof of Theorem 1.3
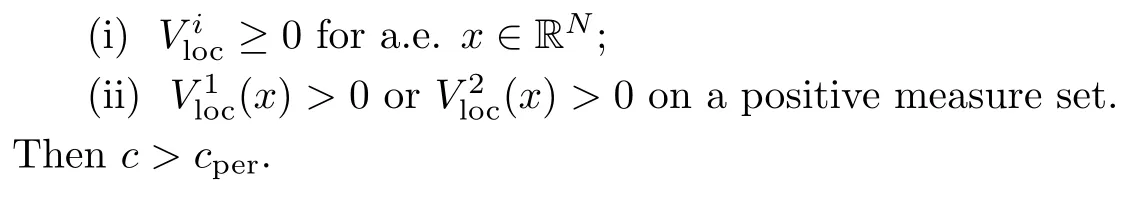
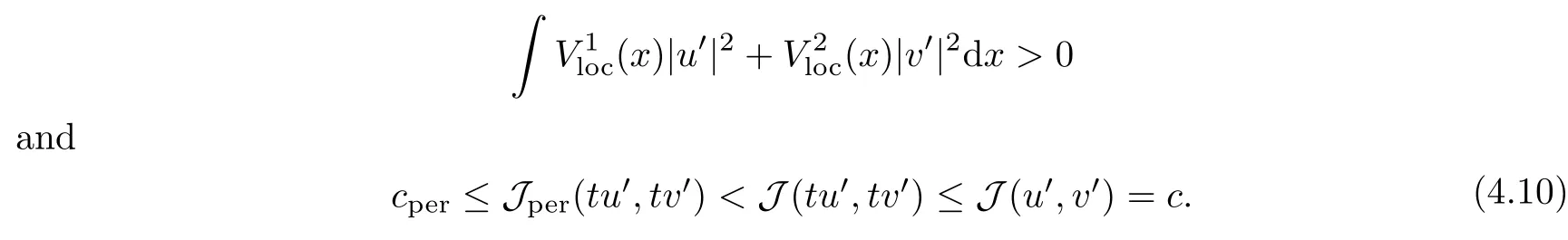
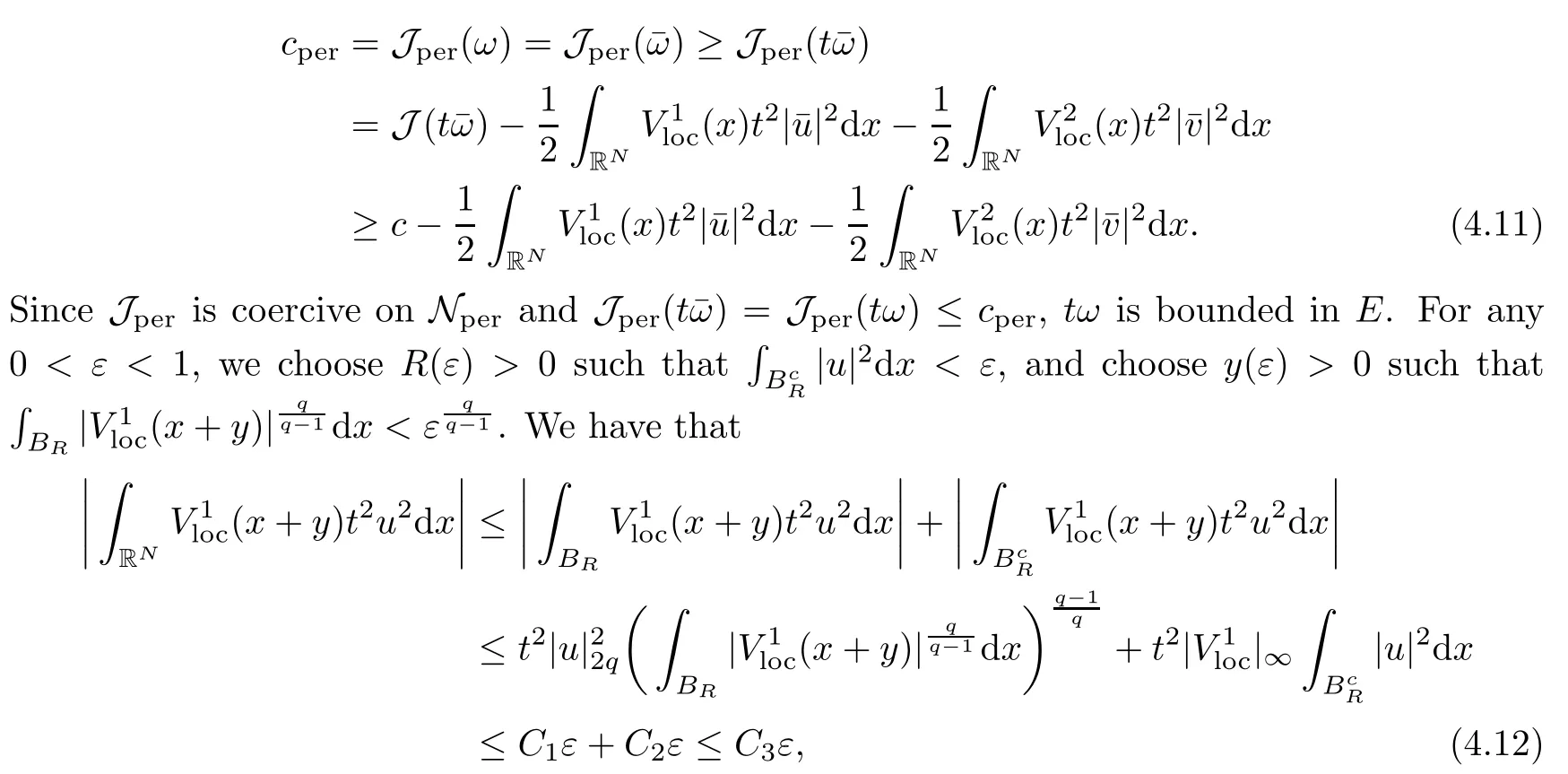

 Acta Mathematica Scientia(English Series)2020年5期
Acta Mathematica Scientia(English Series)2020年5期
