基于ECDLP 的工作量證明方案設(shè)計(jì)*

劉志杰, 張方國, 田海博

1. 中山大學(xué) 數(shù)據(jù)科學(xué)與計(jì)算機(jī)學(xué)院, 廣州510006

2. 廣東省信息安全技術(shù)重點(diǎn)實(shí)驗(yàn)室, 廣州510006

1 引言

由于Koblitz[1]和Miller[2]開創(chuàng)性的工作, 使得已被數(shù)學(xué)家研究了一百多年的橢圓曲線在密碼領(lǐng)域中發(fā)揮重要的作用. 橢圓曲線密碼體制(ECC) 的數(shù)學(xué)基礎(chǔ)是利用橢圓曲線上的點(diǎn)構(gòu)成的Abelian 加法群中的離散對數(shù)的計(jì)算困難性. 換而言之, ECC 的安全性依賴于橢圓曲線離散對數(shù)問題(ECDLP) 的困難性. 在過去的幾十年里, ECC 已經(jīng)成為一種標(biāo)準(zhǔn)化的工具[3], 應(yīng)用于各種密碼協(xié)議和系統(tǒng). 在求解ECDLP 的算法中, 大家公認(rèn)的最有效的算法是基于生日悖論的Pollard rho 算法[4], 其實(shí)質(zhì)是在群元素中尋找匹配或者碰撞, 希望能從這種碰撞中得到碰撞點(diǎn)之間的聯(lián)系進(jìn)而來求解ECDLP. 后來的密碼學(xué)家在此基礎(chǔ)上提出了各種對Pollard rho 算法的改進(jìn)和優(yōu)化方案. Van Oorschot 和Viener[5]等人利用可區(qū)分點(diǎn)碰撞檢測的辦法對Pollard rho 算法進(jìn)行改進(jìn), 證明了該算法在群元素中尋找碰撞的所需要的時間呈線性減少. 同時, 改進(jìn)的Pollard rho 算法可以利用傳統(tǒng)的分布式計(jì)算框架進(jìn)行并行計(jì)算, 每個并行節(jié)點(diǎn)將計(jì)算好的可區(qū)分點(diǎn)存入同一個數(shù)據(jù)庫中, 一旦某一個并行節(jié)點(diǎn)發(fā)現(xiàn)自己存儲的可區(qū)分點(diǎn)已經(jīng)在數(shù)據(jù)庫中, 那么碰撞就找了, 最后計(jì)算出ECDLP 的最終求解. 目前為止, ECDLP 的求解最高記錄是Wenger 和Wolfger[6]等人在2014 年給出的113 bits.

比特幣[7]作為區(qū)塊鏈技術(shù)的一個典型代表, 其共識算法是工作量證明, 礦工們主要是執(zhí)行哈希算法完成這一項(xiàng)工作. 事實(shí)上, 許多分布式計(jì)算問題或困難問題, 都可以作為工作量證明的困難問題. 在區(qū)塊鏈中, 每個礦工打包區(qū)塊的計(jì)算資源可以視為是一種分布式計(jì)算的資源. 例如Primecoin[8]采用數(shù)論問題設(shè)計(jì)一個新的工作量證明方案, 而Chatterjee[9]則是利用NP 完全問題設(shè)計(jì)了一個新的工作量證明方案. 此外, 在區(qū)塊鏈中, 礦工打包區(qū)塊需要消耗大量的計(jì)算資源, 這個過程中造成資源的浪費(fèi)的問題一直受到人們的詬病[10], 因而將分布式計(jì)算問題或困難問題引入到挖礦的過程中, 可以使得挖礦所消耗的能源變的更有意義.

Marcella 和Nadia[11]等人提出了基于離散對數(shù)問題(DLP) 的工作量證明方案, 但是該方案中沒有給出一個從初始點(diǎn)到滿足挑戰(zhàn)難度的可區(qū)分點(diǎn)的快速有效的驗(yàn)證方法. 本文基于一種改進(jìn)的并行的Pollard rho 算法, 提出了基于ECDLP 的工作量證明方案. 特別地, 本文提出了一種思路, 解決了一個區(qū)塊中從初始點(diǎn)到可區(qū)分點(diǎn)的有效驗(yàn)證問題. 另一方面, Certicom[12]公司為ECDLP 挑戰(zhàn)者設(shè)立了豐厚的獎金. 因此, 可以借助區(qū)塊鏈中天然的激勵機(jī)制, 為每位參與挖礦的礦工給予報酬, 從而促使更多的節(jié)點(diǎn)參與到挖礦的過程中來. 同時, 可以促進(jìn)ECDLP 求解算法的軟件或硬件實(shí)現(xiàn)的優(yōu)化, 更好的推動ECDLP求解算法的研究與發(fā)展.

2 預(yù)備知識

2.1 ECC

一般地, 橢圓曲線是指在有限域Fq或F2m上的橢圓曲線. Fq是一個特征q ?=2,3 的有限域, 橢圓曲線E 定義為滿足方程:y2=x3+ax+b, a,b ∈Fq且4a3+27b2?=0 的點(diǎn)(x,y)∈Fq×Fq和特殊點(diǎn)(無窮遠(yuǎn)點(diǎn)) 所組成的集合.

定義在有限域F2m上的非超奇異橢圓曲線E 為滿足方程:y2+xy = x3+ax2+b, a,b ∈F2m且b ?=0 的點(diǎn)(x,y)∈F2m×F2m和特殊點(diǎn)(無窮遠(yuǎn)點(diǎn)) 所組成的集合.

2.2 ECDLP

給定橢圓曲線E 上階為素?cái)?shù)n 的點(diǎn)P, < G > 為P 生成的一個素?cái)?shù)階群. 對于任意Q ∈G, 找一個整數(shù)k, 0 ≤k ≤n, 使得Q=kP, 就是橢圓曲線離散對數(shù)問題.

2.3 ECCp-131

ECCp-131 是Certicom[12]公司設(shè)立的挑戰(zhàn)之一, 目前還沒有被攻破. 該挑戰(zhàn)是定義在有限域Fq上的橢圓曲線, 其中

同時, 給定的素?cái)?shù)階為

對于該挑戰(zhàn)ECCp-131, 點(diǎn)P 和點(diǎn)Q 的值分別是

2.4 Pollard rho 算法

隨機(jī)選取2r 個整數(shù)

并且計(jì)算r 個元素

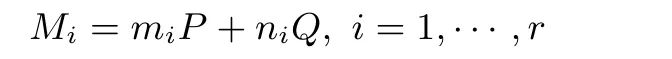
定義一個映射函數(shù)v, 使得G 中的元素均勻地映射到{1,··· ,r} 中, 即

定義隨機(jī)游走迭代函數(shù)F :G →G 為

隨機(jī)選取a0,b0∈{0,1,··· ,n ?1}, 令Y0=a0P +b0Q 作為起始點(diǎn). 每一次迭代中ai,bi的表達(dá)式如下

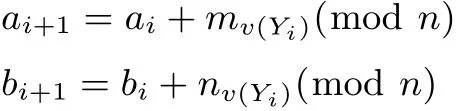
一旦發(fā)生碰撞, 即Yi=Yj(i ?=j), 可以得到如下表達(dá)式

如果gcd(bi?bj,n)=1 則k =(aj?ai)(bi?bj)?1mod n.

2.5 可區(qū)分點(diǎn)碰撞檢測

令D 為G 的一個子集合, 給定一個約束條件d, D 中所有的元素都滿足如下要求:

(1) 對于任意一個可區(qū)分點(diǎn)Yi∈D, 滿足Yi的x 軸坐標(biāo)值小于等于d.

(2) 對于任意一個可區(qū)分點(diǎn)Yi∈D, 滿足Yi=aiP +biQ, ai,bi∈{0,1,··· ,n ?1}.

(3) 一旦發(fā)生碰撞, 即Yi=Yj(i ?=j), 滿足aiP +biQ=ajP +bjQ, gcd(bi?bj,n) =1.

2.6 工作量證明

工作量證明[13]早期是為了防止垃圾郵件和Dos 攻擊而被提出的, 隨后比特幣采用工作量證明作為共識機(jī)制, 使得比特幣在開放的, 去中心的, 互補(bǔ)信任的節(jié)點(diǎn)之間可以達(dá)成共識. 工作量證明由三個函數(shù)組成[14](Gen, Solve, Verify):

(1) c ←Gen(1n): 產(chǎn)生挑戰(zhàn)c 的概率性算法.

(2) s ←Solve(c): 解決挑戰(zhàn)c ←Gen(1n) 得到解s 的算法.

(3) { 接受, 拒絕}←Verify(c,s): 驗(yàn)證挑戰(zhàn)c ←Gen(1n), 是否被s ←Solve(c) 解決的算法.且滿足以下幾點(diǎn)[14]:

(1) 效率性:

(a) Gen(1n) 的運(yùn)算時間復(fù)雜度是O(n).

(b) 對于任意c ←Gen(1n), Solve(c) 的運(yùn)算時間復(fù)雜度是O(t(n)), 其中t 是一個指數(shù)函數(shù).

(c) 對于任意c ←Gen(1n) 和s ←Solve(c), Verify(c,s) 的運(yùn)算時間復(fù)雜度是O(n).

(2) 完備性:

對于任意c ←Gen(1n) 和s ←Solve(c), Pr [Verify(c,s) = 接受] = 1.

(3) 難解性:

l 為任意的多項(xiàng)式, ? 為任意常量且 ? > 0, 當(dāng)給定任意多項(xiàng)式時間 l(n) 的挑戰(zhàn){ci←Gen(1n)}i∈l(n), Solve?l的運(yùn)算時間復(fù)雜度為l(n)t(n)1??, 有Pr[?i Verify(ci,si) = 接受 | (s1,··· ,sl(n))←Solve?l(c1,··· ,cl(n))] <δ(n), 其中δ(n) 是一個可忽略的概率值.

在比特幣中, Gen 函數(shù)的輸出值是前一個區(qū)塊的哈希值. Solve 是由一個難度值d 控制的函數(shù), 礦工需要找到一個隨機(jī)值nonce, 使得SHA-256(c,nonce) < 2256?d. SHA-256 可以視為是一個隨機(jī)數(shù)函數(shù),因此礦工尋找一個滿足要求的隨機(jī)值nonce 的概率是2?d. 換言之, Solve 的運(yùn)算時間復(fù)雜度是O(2d).Verify 函數(shù)是驗(yàn)證(c,nonce) 是否滿足SHA-256(c,nonce) <2256?d, 如果滿足該條件就接受, 否則拒絕.

2.7 激勵機(jī)制

在區(qū)塊鏈中, 當(dāng)每個新區(qū)塊產(chǎn)生后, 區(qū)塊鏈系統(tǒng)都會獎勵找到該區(qū)塊的礦工. 在挖礦的過程中是需要消耗計(jì)算資源和電力的, 因此獎勵也可以作為交易費(fèi)用來資助礦工. 同時, 這種激勵可能有助于鼓勵節(jié)點(diǎn)保持誠實(shí). 另一方面, 每個新區(qū)塊的獎勵也不是固定的, 每開采210 000 個區(qū)塊, 大約需要4 年的時間, 貨幣發(fā)行速率將降低50%. 以比特幣為例, 從2008 年開始計(jì)算, 在其運(yùn)行的第一個四年中, 產(chǎn)生區(qū)塊的礦工將獲得50 個比特幣. 到了2012 年后, 產(chǎn)生區(qū)塊的礦工將獲得25 個比特幣. 依次類推, 產(chǎn)生區(qū)塊的礦工將獲得12.5 個比特幣.

3 方案模型

3.1 用戶關(guān)系模型

本文方案共有3 個參與方, 分別為ECDLP 發(fā)布者, 礦工和驗(yàn)證者. 其中ECDLP 發(fā)布者可以為任何一個需要發(fā)布ECDLP 挑戰(zhàn)的區(qū)塊鏈用戶, 該用戶只需要發(fā)布一個挑戰(zhàn)申明的交易. 挑戰(zhàn)申明交易包含了ECDLP 的初始點(diǎn)P, Q, 可區(qū)分點(diǎn)單價以及一系列固定參數(shù)(mi,ni,Mi, i=1,··· ,r) 等信息, 所有的礦工會將挑戰(zhàn)申明的交易信息記錄到一張?zhí)魬?zhàn)申明表中. 一旦當(dāng)前的ECDLP 的問題被解決了, 他們會選擇下一個ECDLP 挑戰(zhàn)重新開始計(jì)算. 礦工的主要責(zé)任是執(zhí)行隨機(jī)游走迭代函數(shù)F, 計(jì)算符合挑戰(zhàn)難度要求的可區(qū)分點(diǎn), 并將該可區(qū)分點(diǎn)的x 軸坐標(biāo)值打包放到區(qū)塊頭中, 然后向全網(wǎng)廣播. 驗(yàn)證者的主要責(zé)任是驗(yàn)證新區(qū)塊頭中可區(qū)分點(diǎn)是否滿足要求, 如果滿足則接受該新區(qū)塊, 否則拒絕. 同時, 驗(yàn)證者會驗(yàn)證所有的可區(qū)分點(diǎn)在區(qū)塊鏈上是否存在碰撞, 一旦發(fā)現(xiàn)了碰撞, 會發(fā)布一個碰撞的交易.

3.2 區(qū)塊頭結(jié)構(gòu)

礦工產(chǎn)生滿足挑戰(zhàn)難度的可區(qū)分點(diǎn)之后需要將其打包到新區(qū)塊的區(qū)塊頭中, 因此本文重新設(shè)計(jì)了區(qū)塊鏈中的區(qū)塊頭結(jié)構(gòu), 如圖1所示.

圖1 區(qū)塊鏈頭部結(jié)構(gòu)Figure 1 Head structure of blockchain

(1) VERSION: 記錄區(qū)塊版本號.

(2) PREVIOUS: 記錄前一個區(qū)塊的哈希值.

(3) NONCE: 記錄隨機(jī)數(shù).

(4) TARGET: 記錄該區(qū)塊工作量證明算法的難度閾值.

(5) TIME: 記錄時間戳.

(6) POINT: 記錄符合挑戰(zhàn)難度目標(biāo)的可區(qū)分點(diǎn)x 軸坐標(biāo)值.

(7) LISTS: 記錄存儲特殊點(diǎn)的游走路徑.

(8) MERKLE ROOT: 記錄Merkle 樹根節(jié)點(diǎn)的哈希值.

上述提及的區(qū)塊頭部中的PREVIOUS 字段用于作為一個挑戰(zhàn)c, 并且和NONCE 字段值一起計(jì)算出初始點(diǎn)Y0. POINT 字段只需要存儲可區(qū)分點(diǎn)的x 軸坐標(biāo)值, 因?yàn)樵谂鲎矙z測的過程中, 只需要檢測兩個可區(qū)分點(diǎn)是否有相同的x 軸坐標(biāo)值即可, 同時也減少了頭部占用的存儲空間. LISTS 字段是一個r 維向量, 由r 個整數(shù)組成(s1,··· ,sr), 依次代表著從M1到Mr的累加次數(shù), 區(qū)塊鏈中的驗(yàn)證節(jié)點(diǎn)可以通過LISTS 字段快速驗(yàn)證特殊點(diǎn)產(chǎn)生所需要的工作量, 為每個新生區(qū)塊提供工作量證明.

3.3 挑戰(zhàn)難度關(guān)系模型

為了使得工作量證明中挑戰(zhàn)難度容易受控制, 本文方案規(guī)定滿足當(dāng)前挑戰(zhàn)難度的可區(qū)分點(diǎn)的x 軸坐標(biāo)值小于等于難度閾值TARGET. 難度閾值是礦工打包區(qū)塊速率的重要參考指標(biāo), 它決定了礦工大約需要經(jīng)過多少次計(jì)算才能產(chǎn)生一個合法的區(qū)塊. 在比特幣系統(tǒng)中, 每個區(qū)塊生成的時間大約為10 分鐘. 若要維持新區(qū)塊的產(chǎn)生速率約為10 分鐘一個區(qū)塊, 難度閾值必須根據(jù)全網(wǎng)算力的變化進(jìn)行調(diào)整. 難度閾值的調(diào)整是在每個完整節(jié)點(diǎn)中獨(dú)立自動發(fā)生的, 每當(dāng)生成了2016 個區(qū)塊, 所有的礦工都會按一個規(guī)定好的公式進(jìn)行自動難度調(diào)整. 這個公式是由產(chǎn)生最新2016 個區(qū)塊所花費(fèi)的時長與期望時長(20 160 分鐘) 比較得出的, 具體表達(dá)式如下:

其中actual_time 為產(chǎn)生最新2016 個區(qū)塊所花費(fèi)的時長, expected_time 為期望時長. 若在區(qū)塊鏈系統(tǒng)初始化時, 我們以Certicom[12]公司設(shè)立的ECCp-131 作為默認(rèn)挑戰(zhàn), 同時維持新區(qū)塊的產(chǎn)生速率約為10 分鐘生產(chǎn)一個區(qū)塊, TARGET 值的初始值應(yīng)為77766331555005660491798357300000.

3.4 工作量驗(yàn)證模型

雖然驗(yàn)證者需要驗(yàn)證滿足挑戰(zhàn)難度要求的可區(qū)分點(diǎn)YD的x 軸坐標(biāo)值在二進(jìn)制編碼形式下, 由最高位開始依次d 個二進(jìn)制位都為零, 但是驗(yàn)證者卻無法確定YD是由一個合法的初始點(diǎn)Y0開始計(jì)算得到的.于是一個不誠實(shí)的礦工可以預(yù)先計(jì)算好一個滿足挑戰(zhàn)難度的可區(qū)分點(diǎn), 然后將該點(diǎn)打包到區(qū)塊頭部并發(fā)布到網(wǎng)絡(luò)中去. 為了避免這樣的情況發(fā)生, 驗(yàn)證者需要記錄下礦工提供從Y0到Y(jié)D的游走路徑(s1,··· ,sr),然后驗(yàn)證者沿著該路徑一步一步計(jì)算到Y(jié)D, 判斷YD是否付出了足夠的工作量. 但是這種驗(yàn)證方法并不是有效的, 不滿足工作量證明中“難于計(jì)算, 易于驗(yàn)證” 的要求.

3.5 激勵模型

本方案中的激勵方案共分為兩個部分, 第一部分是礦工成功打包區(qū)塊后所獲得的獎勵, 第二部分是礦工成功計(jì)算出已發(fā)布問題的可區(qū)分點(diǎn)后所獲得的獎勵. 在區(qū)塊鏈中, 為了鼓勵節(jié)點(diǎn)保持誠實(shí), 當(dāng)每個新區(qū)塊的產(chǎn)生后, 區(qū)塊鏈系統(tǒng)都會獎勵給打包該區(qū)塊的礦工. 對于第一部分, 本文采用與比特幣系統(tǒng)相同的激勵方案, 每開采210 000 個區(qū)塊, 大約需要4 年的時間, 貨幣發(fā)行速率將降低50%, 并且在第一個四年中,產(chǎn)生區(qū)塊的礦工將獲得50 個鏈上流通的貨幣.

對于第二部分, 當(dāng)區(qū)塊鏈系統(tǒng)中有已發(fā)布的ECDLP 挑戰(zhàn)后, 礦工成功計(jì)算出符合要求的可區(qū)分點(diǎn)后會獲得相應(yīng)的第二部分的獎勵, 該獎勵金額由ECDLP 發(fā)布者決定. ECDLP 發(fā)布者在發(fā)布挑戰(zhàn)交易時,需要指定每個可區(qū)分點(diǎn)的金額, 當(dāng)?shù)V工成功計(jì)算出符合要求的可區(qū)分點(diǎn)時, 該礦工會獲得該金額. 如果當(dāng)前區(qū)塊鏈系統(tǒng)中沒有任何節(jié)點(diǎn)發(fā)布ECDLP 挑戰(zhàn), 礦工將計(jì)算默認(rèn)的ECDLP 挑戰(zhàn), 但是當(dāng)?shù)V工成功計(jì)算出符合要求的可區(qū)分點(diǎn)時, 礦工獲得第二部分的獎勵的金額為0.

4 具體設(shè)計(jì)

本文中的方案設(shè)計(jì)主要包括挑戰(zhàn)申明交易發(fā)布, 礦工挖礦, 區(qū)塊驗(yàn)證, 碰撞檢測和EDCLP 求解五個模塊. 本小節(jié)將會更為詳細(xì)的闡述每個模塊的具體實(shí)現(xiàn)或具體使用的參數(shù).

4.1 挑戰(zhàn)申明交易發(fā)布

Teske[15]通過大量的實(shí)驗(yàn)表明, 在基于adding walks 的Pollard rho 算法中群G 的劃分大小為30 是最適合的選擇. Teske 的實(shí)驗(yàn)結(jié)果顯示, 當(dāng)r = 30 時, 找到碰撞所需要計(jì)算量是最小的. 因此在ECDLP 發(fā)布者需要在挑戰(zhàn)申明交易中輸入自身的ECDLP 挑戰(zhàn)之后, 額外要輸入預(yù)計(jì)算好的30 組固定參數(shù)(mi,ni,Mi), i=1,··· ,30, 具體步驟如下:

(1) 隨機(jī)選取整數(shù)α ∈{0,1,··· ,n ?1}, 令Q′=αQ 且P ?=Q′.

(2) 隨機(jī)選取60 個整數(shù)mi,ni∈{0,1,··· ,n ?1}, i=1,··· ,30.

(3) 計(jì)算Mi=miP +niQ′.

(4) 向挑戰(zhàn)申明交易輸入ECDLP 參數(shù)(Mi,P,Q′) 和單個可區(qū)分點(diǎn)金額.

(5) 發(fā)布挑戰(zhàn)申明交易.

(6) 礦工接收到該交易, 并記錄到挑戰(zhàn)申明表中.

由于區(qū)塊鏈上的信息都是公開透明的, 在發(fā)生可區(qū)分點(diǎn)碰撞時且網(wǎng)絡(luò)時延比較大的情況下, 惡意的用戶可能可以預(yù)先一步將解決ECDLP 的成果占為己有, 惡意用戶可以通過碰撞點(diǎn)計(jì)算出ECDLP 的挑戰(zhàn)結(jié)果, 然后去冒領(lǐng)完成該挑戰(zhàn)的獎勵. 因此為了避免這樣的情況發(fā)生, ECDLP 發(fā)布者在公布自身的ECDLP 挑戰(zhàn)之前需要對Q 做盲化處理, 這樣即便找到了碰撞, 也只有ECDLP 發(fā)布者能獲得真正的挑戰(zhàn)成果. 當(dāng)找到碰撞時, ECDLP 發(fā)布者進(jìn)行一次去盲的操作便可以計(jì)算出最終的解. 同時, 所有挑戰(zhàn)申明表中第一條都是默認(rèn)的ECDLP 挑戰(zhàn)參數(shù), 以保證開始階段礦工能正常的挖礦. 需要注意的是, 每個礦工維護(hù)的挑戰(zhàn)申明表中都有一個相同默認(rèn)挑戰(zhàn), 當(dāng)?shù)V工收到新的挑戰(zhàn)申明時, 會向表中插入該新的挑戰(zhàn)申明,并記錄相應(yīng)的時間戳.

4.2 礦工挖礦

礦工主要是計(jì)算出滿足挑戰(zhàn)難度的可區(qū)分點(diǎn), 將計(jì)算得到的可區(qū)分點(diǎn)打包放入?yún)^(qū)塊頭中, 并發(fā)布到網(wǎng)絡(luò)中去. 此外, 區(qū)塊鏈上的信息都是公開透明的, 為了避免惡意用戶預(yù)先計(jì)算好滿足要的可區(qū)分點(diǎn), 方案規(guī)定一個合法的初始點(diǎn)Y0必須從最新區(qū)塊的區(qū)塊頭中計(jì)算獲得. 具體步驟如圖2 所示.

圖2 礦工挖礦流程圖Figure 2 Mining procedure process

(1) 選擇挑戰(zhàn)申明表第一個未被求解的ECDLP 挑戰(zhàn)參數(shù). 當(dāng)申明表中沒有未被求解的ECDLP 挑戰(zhàn), 礦工會選擇申明表中的默認(rèn)挑戰(zhàn)參數(shù)進(jìn)行挖礦.

(2) 獲取當(dāng)前最新區(qū)塊的哈希值作為挑戰(zhàn)c 和選取隨機(jī)數(shù)n, 令(a0,b0)=Hash(c||n).

(3) 令i=0, 且s1=s2=···=s30=0.

(4) 計(jì)算Y0=a0P +b0Q′.

(5) 若Y0滿足當(dāng)前難度下的可區(qū)分點(diǎn)要求, 則進(jìn)入第(7) 步, 否則進(jìn)入下一步.

(6) 迭代計(jì)算: Yi+1=F(Yi)=Yi+Mv(Yi), sv(Yi)=sv(Yi)+1, i=i+1.

(7) 若Yi+1滿足當(dāng)前挑戰(zhàn)難度下的可區(qū)分點(diǎn)要求, 則進(jìn)入下一步, 否則返回到第(6) 步.

(8) 將游走軌跡(s1,s2,··· ,s30) 寫入LISTS 字段, 隨機(jī)數(shù)n 寫入NONCE 字段, 同時打包可區(qū)分點(diǎn)Yi+1的x 軸坐標(biāo)值到區(qū)塊頭中, 打包區(qū)塊并發(fā)布到全網(wǎng)中.

4.3 區(qū)塊驗(yàn)證

區(qū)塊鏈驗(yàn)證節(jié)點(diǎn)需要驗(yàn)證礦工發(fā)布的區(qū)塊內(nèi)容是否滿足要求, 具體步驟如圖3 所示:

(1) 計(jì)算每個Mi,i = 1,··· ,30 的預(yù)計(jì)算標(biāo)量乘查找表, 并存儲到本地(該步驟為預(yù)計(jì)算步驟, 對于每一個ECDLP 挑戰(zhàn), 該步驟只需要執(zhí)行一次).

(2) 驗(yàn)證POINT 字段中的數(shù)值是否滿足挑戰(zhàn)難度值要求, 若滿足則進(jìn)行下一步, 否則直接拋棄, 驗(yàn)證階段結(jié)束.

(3) 獲取當(dāng)前最新一塊區(qū)塊的哈希值, 并驗(yàn)證該值是否與PREVIOUS 字段值相等, 若相等則進(jìn)行下一步, 否則直接拋棄, 驗(yàn)證階段結(jié)束.

(4) 提取PREVIOUS 字段值作為挑戰(zhàn)c 和NONCE 字段值n, 計(jì)算Hash(c||n)=(a0,b0).

(5) 計(jì)算Y0=a0P +b0Q′.

(6) 通過(s1,s2,··· ,s30) 查表并計(jì)算Y′=Y0+s1M1+s2M2+···+s30M30.

(7) 判斷Y′的x 軸坐標(biāo)值是否與POINT 字段中的值相等, 若相等則進(jìn)行下一步, 否則直接拋棄, 驗(yàn)證階段結(jié)束.

(8) 驗(yàn)證POINT 字段中的數(shù)值是否滿足挑戰(zhàn)難度值的要求, 若滿足則接受該區(qū)塊, 驗(yàn)證階段結(jié)束, 否則直接拋棄, 驗(yàn)證階段結(jié)束.

4.4 碰撞檢測

驗(yàn)證者在區(qū)塊驗(yàn)證結(jié)束之后需要將礦工計(jì)算的可區(qū)分點(diǎn)存儲到本地?cái)?shù)據(jù)庫中, 其目的是用于碰撞檢測. 如果當(dāng)前計(jì)算的是默認(rèn)ECDLP 挑戰(zhàn)參數(shù), 驗(yàn)證者則不進(jìn)行碰撞檢測, 否則驗(yàn)證者需要對該可區(qū)分點(diǎn)做一些預(yù)處理, 把處理后的信息存儲到本地?cái)?shù)據(jù)庫中. 一旦發(fā)現(xiàn)碰撞, 驗(yàn)證者就會發(fā)布一個碰撞交易, 通知全網(wǎng)用戶該ECDLP 挑戰(zhàn)已被求解. 礦工會選擇挑戰(zhàn)申明表中下一個未被求解的挑戰(zhàn)繼續(xù)挖礦. 需要注意的是, 碰撞檢測預(yù)處理操作是緊接著在區(qū)塊驗(yàn)證完成以后進(jìn)行的, 具體步驟如圖4 所示.

(1) 檢測是否為默認(rèn)的ECDLP 挑戰(zhàn), 如果是則直接拋棄, 檢測結(jié)束, 否則進(jìn)行下一步.

(2) 計(jì)算a′=a0+s1m1+s2m2+···+s30m30(modn).

(3) 計(jì)算b′=b0+s1n1+s2n2+···+s30n30(modn).

(4) 計(jì)算Y′′=a′P +b′Q′.

(5) 判斷Y′′是否與Y′相等, 若相等則進(jìn)行下一步, 否則直接拋棄, 檢測結(jié)束.

(6) 存儲Y′的x 軸坐標(biāo)值x′, a′和b′到本地?cái)?shù)據(jù)庫中.

(7) 檢測是否存在碰撞, 若碰撞則進(jìn)行下一步, 否則檢測結(jié)束.

(8) 提取出碰撞點(diǎn)的信息x′′軸坐標(biāo)值, a′′和b′′.

(9) 判斷x′′是否與x′相等, 若相等則進(jìn)行下一步, 否則直接拋棄, 檢測結(jié)束.

(10) 判斷等式gcd(b′?b′′,n)=1 是否成立, 若成立則進(jìn)行下一步, 否則直接拋棄, 檢測結(jié)束.

(11) 計(jì)算k′=(a′′?a′)(b′?b′′)?1mod n.

(12) 判斷等式Q′=k′P 是否成立.

(13) 若成立, 輸入k′, Q′和P 到碰撞交易中, 然后向全網(wǎng)發(fā)布該交易, 否則直接拋棄, 檢測結(jié)束.

4.5 ECDLP 求解

當(dāng)ECDLP 發(fā)布者接收到碰撞交易時, 他將驗(yàn)證該交易的正確性. 若通過驗(yàn)證, 將進(jìn)行最后的去盲操作, 進(jìn)而得到最終的ECDLP 求解值, 具體步驟如下:

(1) 計(jì)算Q′′=k′P, 如果Q′′=Q′, 進(jìn)行下一步, 否則求解結(jié)束.

(2) 計(jì)算k =α?1k′.

(3) 若Q=kP, 則求解ECDLP 成功, 結(jié)束, 否則求解失敗, 結(jié)束.

5 驗(yàn)證區(qū)塊效率與安全分析

5.1 驗(yàn)證區(qū)塊效率分析

驗(yàn)證者接收到礦工新發(fā)布的區(qū)塊時, 需要驗(yàn)證YD=Y0+s1M1+s2M2+···+srMr, 因此驗(yàn)證者需要計(jì)算r 次標(biāo)量乘運(yùn)算和r+1 次點(diǎn)加運(yùn)算. 其中r 次標(biāo)量乘運(yùn)算是r 個固定點(diǎn)標(biāo)量乘, 于是可以利用查找表的方式進(jìn)行加速計(jì)算, 為每個固定點(diǎn)Mi,i = 1,··· ,r 建立一個查找表, 當(dāng)計(jì)算siMi的值時, 驗(yàn)證者只需要通過si進(jìn)行查表即可. 此外, 由于每個標(biāo)量乘是相互獨(dú)立的, 因此驗(yàn)證者可以并行查找和計(jì)算每個siMi的值, 然后進(jìn)行一次求和, 進(jìn)一步提高驗(yàn)證上述等式的速度.

以ECCp-131 作為例子, 在單線程情況下, 平臺為Ubuntu 18.04 LTS, 處理器為Intel Core i7-782x(Skylake-X), 3.60 GHz 并且內(nèi)存為64 GB, 驗(yàn)證等式Y(jié)D= Y0+s1M1+s2M2+···+srMr所消耗的時間約為81.45 ms. 同時在相同的平臺下, 計(jì)算一次SHA-256 所消耗的時間約為0.013 ms. 本方案的驗(yàn)證速度與比特幣系統(tǒng)的中計(jì)算SHA-256 的驗(yàn)證速度相比較還是有較大的差距, 但是該方案具有一定的實(shí)用性, 并且從實(shí)踐中驗(yàn)證了本方案達(dá)到“難于計(jì)算卻易于驗(yàn)證” 的目標(biāo).

5.2 驗(yàn)證區(qū)塊安全分析

定理1 如果存在惡意的礦工把一個預(yù)計(jì)算好滿足挑戰(zhàn)難度的可區(qū)分點(diǎn)構(gòu)造一個合法的新區(qū)塊并發(fā)布到網(wǎng)絡(luò)中, 這個新區(qū)塊被全網(wǎng)絡(luò)接收的概率是可以忽略的.

證明: 對于惡意的礦工來說, 他需要找到一條游走路徑(s1,s2,··· ,s30) 使得他預(yù)計(jì)算好的可區(qū)分點(diǎn)Y′D滿足Y′D= Y0+ s1M1+ s2M2+ ··· + s30M30, 其中初始點(diǎn)Y0是一個合法的初始點(diǎn), 即礦工選取最新一塊區(qū)塊的哈希值作為挑戰(zhàn)c 和隨機(jī)選取一個nonce 值n, 令Hash(c||n) = (a0,b0) 并計(jì)算Y0= a0P +b0Q′. 如果惡意的礦工可以在多項(xiàng)式時間內(nèi)找到這樣的一條游走路徑, 那么ECDLP 就被解決.

6 總結(jié)

本文基于ECDLP 設(shè)計(jì)一種工作量證明方案. 其結(jié)合并行的Pollard rho 算法提出了一個新的思路,有效解決了一個區(qū)塊中從初始點(diǎn)到可區(qū)分點(diǎn)中有效計(jì)算的問題. 本文的方案通過記錄區(qū)分點(diǎn)的游走路徑的和結(jié)合固定點(diǎn)標(biāo)量乘查找表的辦法, 實(shí)現(xiàn)快速驗(yàn)證區(qū)塊的功能. 本文設(shè)計(jì)的方案不僅可以作為一種新的在區(qū)塊鏈中的共識算法, 還可以為用戶提供一種解決ECDLP 困難問題的工具.