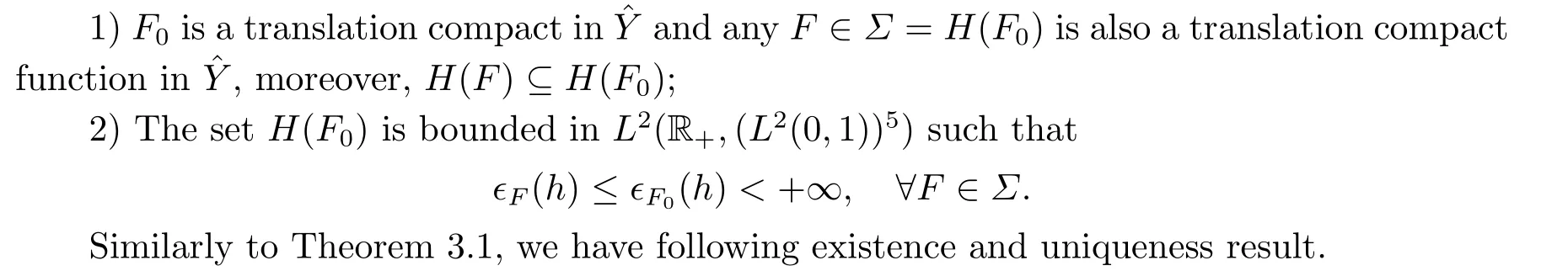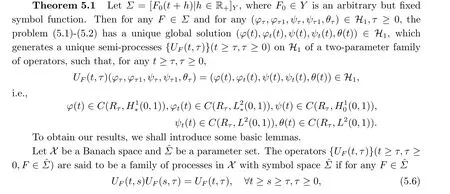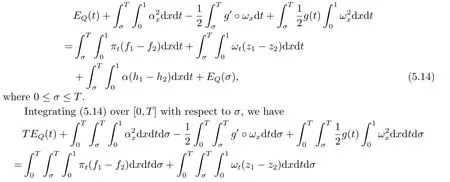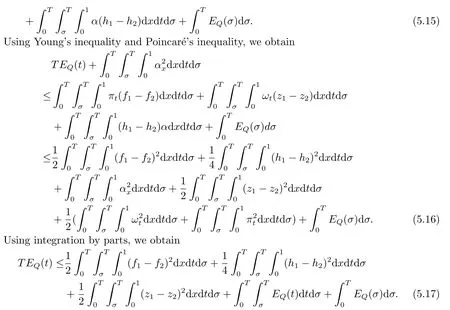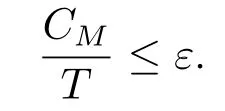Global Existence,Asymptotic Behavior and Uniform Attractor for a Non-Autonomous Thermoelastic Timoshenko System of Type I with a Memory Term
QIN Yuming(秦玉明),DU Yachun(杜雅純)
(College of Science,Donghua University,Shanghai 201620,China)
Abstract: In this article,we consider a non-autonomous Timoshenko system of thermoelasticity of type I with memory type.We first establish the global existence of solutions using the semi-group theory.And then we obtain asymptotic behavior of the solution.Last,we prove the existence of a uniform attractor by using the method of uniform contractive functions.
Key words: Timoshenko system;Global existence;Asymptotic behavior;Uniform attractor;Semigroup method
1.Introduction
Timoshenko[17]developed a simple model to describe the transverse vibration of a beam,whose system of coupled hyperbolic equations are given by
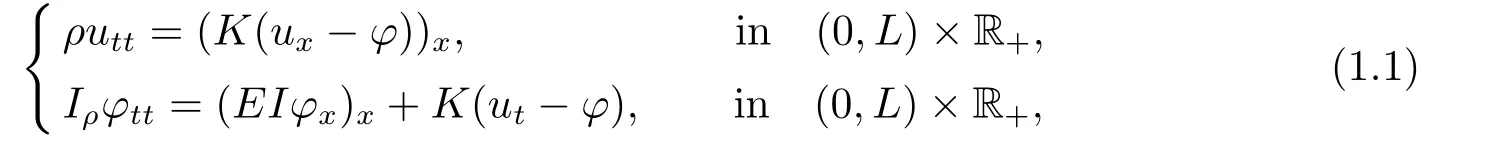
together with boundary conditions of the form
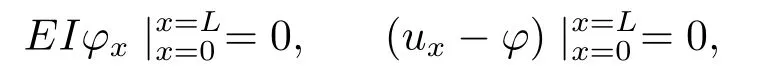
wheretis the time variable andxdenotes the space variable along the beam of lengthL,uis the transverse displacement of the beam andφdenotes the rotation angle of the filament of the beam.The coefficientsρ,Iρ,E,IandKare respectively the density (the mass per unit length),the polar moment of inertia of a cross section,Young’s modulus of elasticity,the moment of inertia of a cross,and the shear modulus.System (1.1) with the above boundary conditions,is conservative and the natural energy of the beam is given by
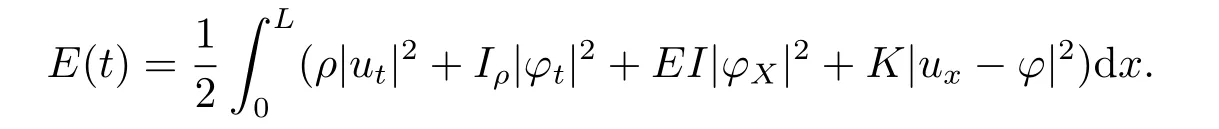
System(1.1)with various initial conditions and boundary conditions has been studied by many mathematicians and asymptotic behavior of solutions has been established.Kim and Renardy[7]considered system (1.1) with two boundary controls of the form
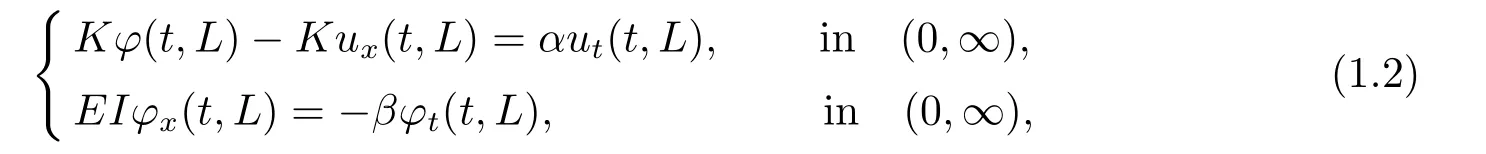
and used the multiplier techniques to establish an exponential decay result for the natural energy of system (1.1).They also provided numerical estimates to the eigenvalues of the operator associated with system (1.1).
Concerning stabilization via classical heat effect,Muńoz Rivera and Racke[10]investigated the system
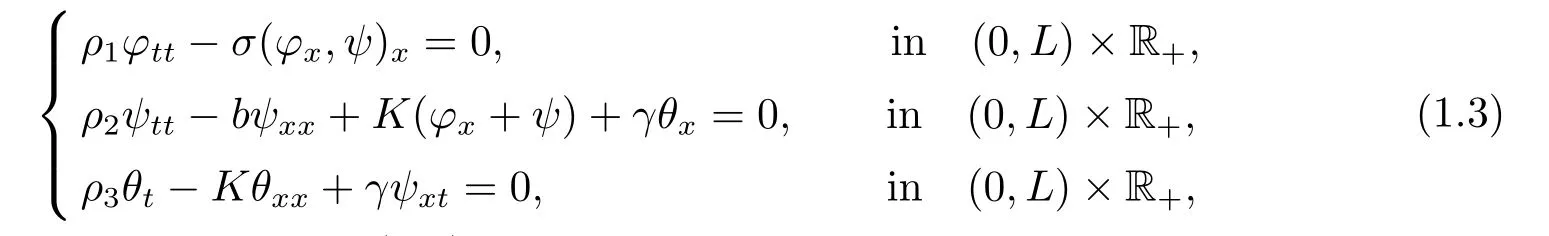
whereφ,ψandθare functions of(x,t)which model the transverse displacement of the beam,the rotation angle of the filament and difference temperature,respectively.Under appropriate conditions onσ,ρ1,b,K,γ,they proved several exponential decay results for the linearized system and non-exponential stability results for the case of different wave speeds.
Messaoudi,Pokojovy and Said-Houari[8]studied Timoshenko systems of thermoelasticity with second sound
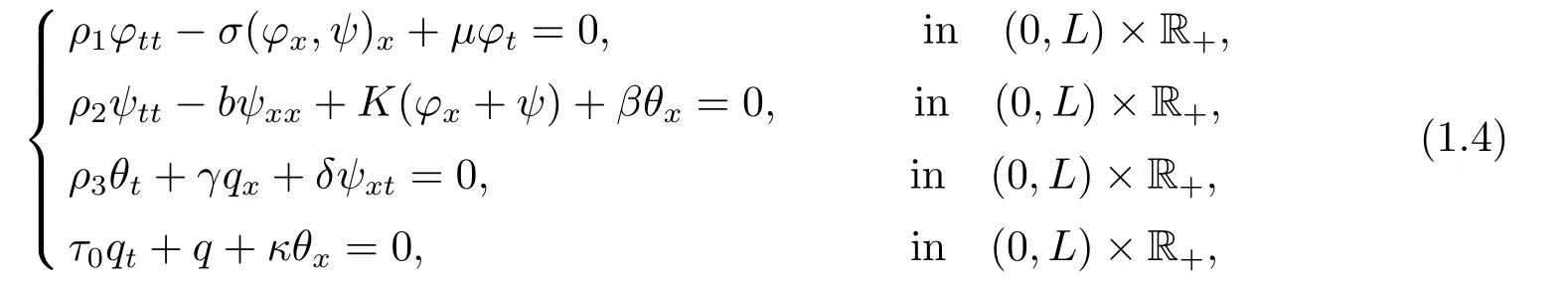
whereφ=φ(x,t)is the displacement vector,ψ=ψ(x,t)is the rotation angle of the filament,θ=θ(x,t)is the temperature,q=q(x,t)is the heat flux vector andρ1,ρ2,ρ3,b,K,γ,δ,κ,μ,τ0are positive constants.The nonlinear functionσis assumed to be sufficiently smooth and satisfies
σφx(0,0)=σψ(0,0)=K,
and
σφxφx(0,0)=σφxψ(0,0)=σψψ=0.
Ammar-Khodja et al.[2]considered a linear Timoshenko-type system with memory of the form
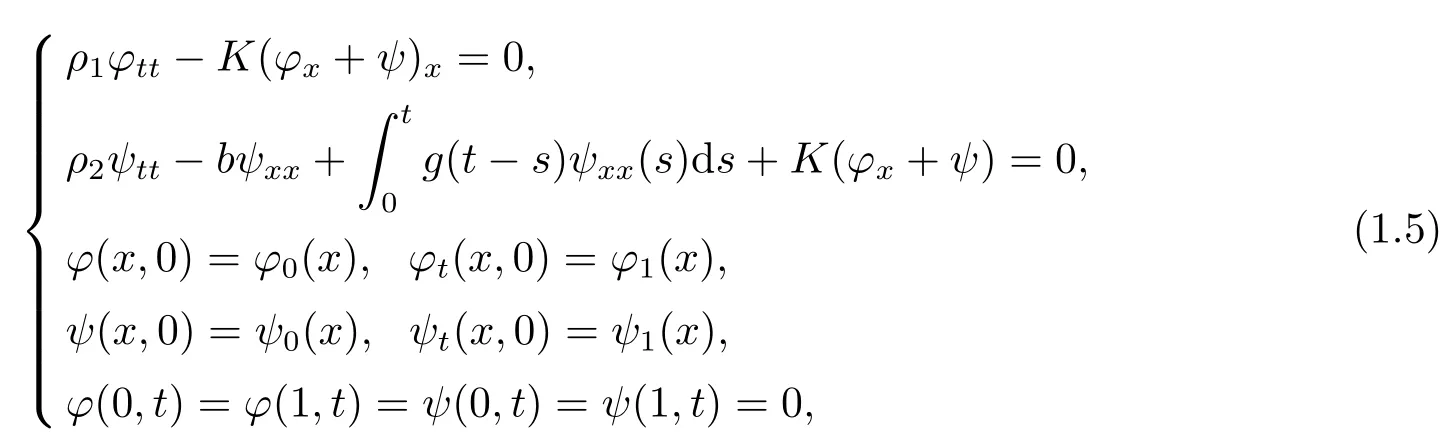
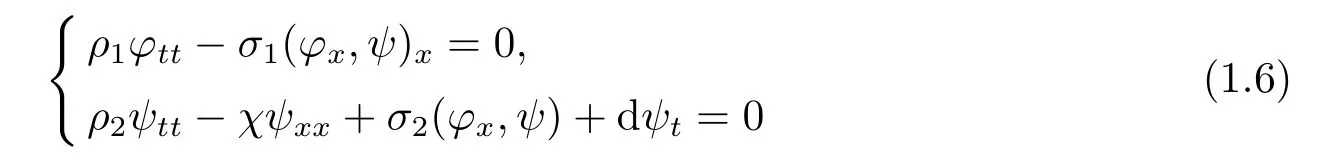
in a one-dimensional bounded domain.The dissipation is produced here through a frictional damping which is only present in the equation for the rotation angle.
Recently,Fernández Sare and Rivera[4]considered a Timoshenko-type system with a past history of the for m
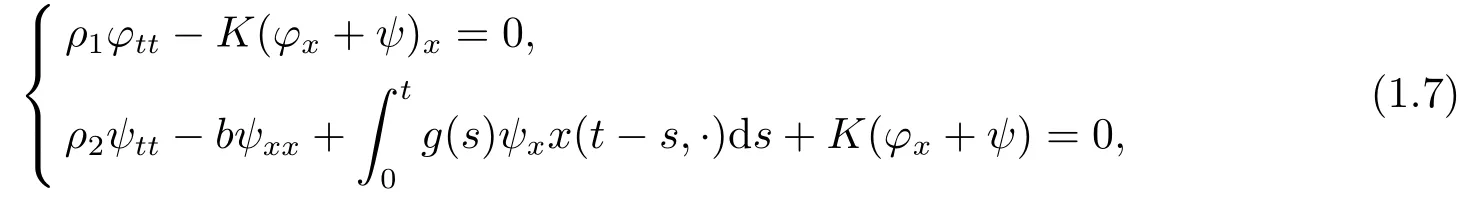
whereρ1,ρ2,K,bare positive constants andgis a positive twice differentiable function satisfying,for some constantsk0,k1,k2>0,
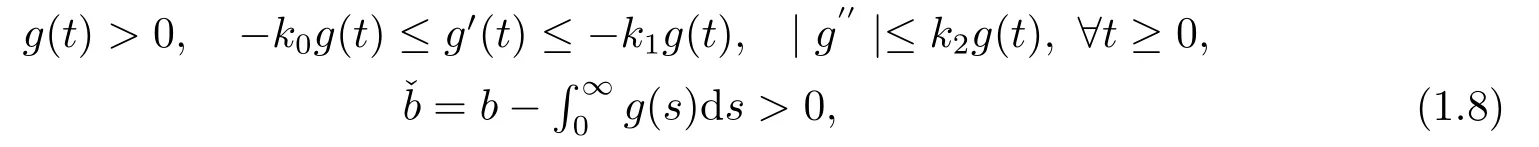
and showed that the dissipation given by the history term is strong enough to stabilize the system exponentially if and only if the wave speeds are equal.They also proved that the solution decays polynomially for the case of different wave speeds.
Guesmia[5]consider a Timoshenko system in one-dimensional bounded domain with infinite memory and distributed time delay both acting on the equation of the rotation angle
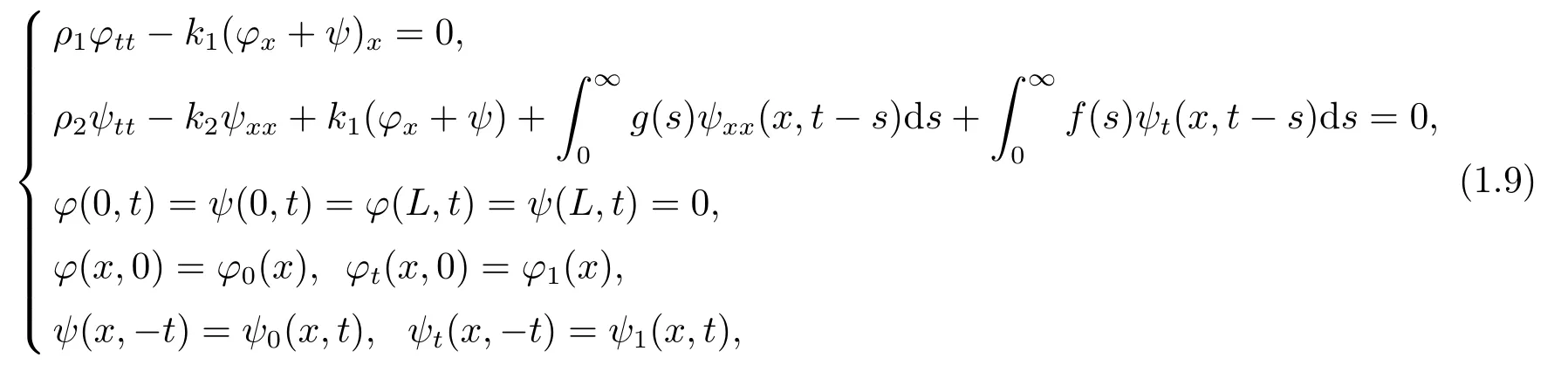
Recently,QIN and WEI[16]established the global existence and asymptotic behavior of solutions by using the semigroup method and multiplicative techniques,then proved the existence of a uniform attractor for a non-autonomous thermoelastic system by using the method of uniform contractive functions.QIN and MA[15]presented recent results on some global well-posedness and asymptotic behavior of the solutions to non-classical thermo(visco)elastic models.They established the global existence result for the higher-dimensional linear thermoviscoelastic equations of type III by using a semigroup approach.Using the multiplier techniques and Lyapunov methods,they proved that the energy goes to zero exponentially by introducing a velocity feedback on a part of the boundary of a thermoelastic body,which is clamped along the rest of its boundary to increase the loss of energy.For more related results,we refer to [12-14,18].
In the present paper,we consider a non-autonomous Timoshenko-type system of thermoelasticity of type I with memory term:
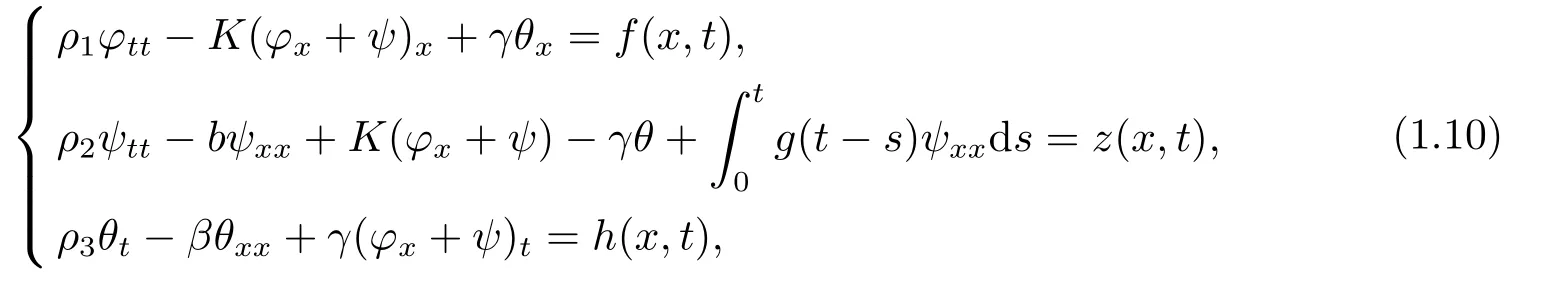
whereφ=φ(x,t),ψ=ψ(x,t),θ=θ(x,t),(x,t)∈(0,1)×(0,+∞) andρ1,ρ2,ρ3,K,b,β,γare positive constants.In this system,represents a memory term,andf,z,hare forcing terms.We consider (1.10) coupled with initial data
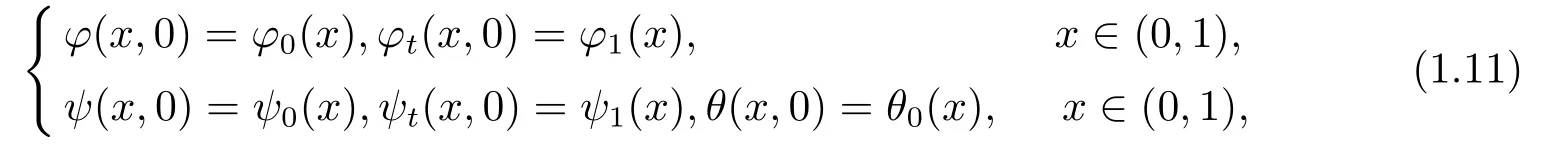
and Neumann-Dirichlet-Dirichlet boundary conditions
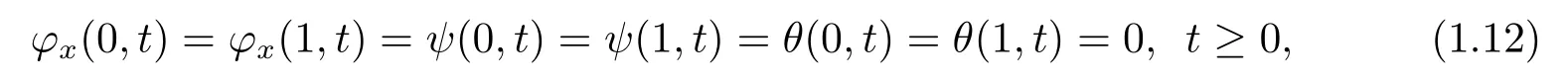
and establish a general stability result irrespective of the wave speeds of the system.It is imperative to mention that the boundary conditions (φx(0,t)=φx(1,t)=ψ(0,t)=ψ(1,t)=0) are equivalent to the sliding end boundary condition on Timoshenko system.
2.Preliminaries
In this section,we present some materials needed for our main results.For simplicity of notations,hereafter we denote by∥.∥qthe norm of Lebesgue spaceLq(?),and by∥.∥2the norm of Lebesgue spaceL2(?).
In order to deal with the memory term,we assume that the functiongsatisfies the following assumptions:
(H1)g:is aC1decreasing function satisfying:
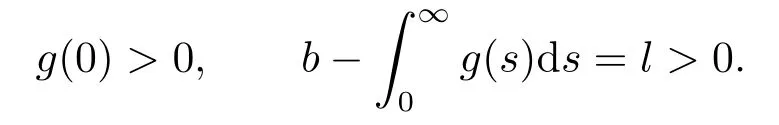
(H2) There exists a nonincreasing differentiable functionξ:,and a constantM,satisfying:
|ξ(t)| Meanwhile,from the first equation in (1.10) and the boundary conditions (1.12),it follows that Obviously,using the initial data ofφ,we obtain Consequently,as in [6],if we let then we obtain In this section,we shall investigate the global well-posedness of problem (1.10) with the variable norm technique,we start with the vector functionU=(φ,u,ψ,v,θ)T,whereu=φt,v=ψt.We introduce as in [6], Then we define the energy space Theorem 3.1Assume thatf(x,t),z(x,t),h(x,t)∈C1([0,+∞),L2(0,1)),and(H1)(H2)are satisfied.Then,for anyU0∈D(A),there exists a unique solutionU(t) of problem (3.1)satisfying In this section,we shall state and prove our decay results.To this end,we need now to establish several lemmas. Lemma 4.1Let (φ,ψ,θ) be the solution of problem (1.10)-(1.12).Then the energy functional defined by satisfies ProofMultiplying the first three equations in (1.10) byφt,ψtandθ,respectively,and integrating by parts over (0,1),and using the boundary conditions,we obtain Lemma 4.2Let (φ,ψ,θ) be the solution of problem (1.10)-(1.12).Then,the functional ProofA direct computations,and using (1.10),we set Using Young’s inequality,for anyε1>0,we obtain Lemma 4.3Let(φ,ψ,θ)be the solution of problem(1.10)-(1.12).Then,the functional ProofTaking a derivative ofF2int,using (1.10) and integrating by parts,we obtain Lemma 4.4Let(φ,ψ,θ)be the solution of problem(1.10)-(1.12).Then,for anyt0>0,the functional ProofDifferentiatingF3int,taking into account(1.10),and using integrating by parts together with the boundary conditions,we obtain Lemma 4.5Let(φ,ψ,θ)be the solution of problem(1.10)-(1.12).Then,the functional ProofDirect differentiation ofF4int,using(1.10)and integration by parts,we obtain Theorem 4.1LetU0∈D(A),assume that hypotheses(H1)and(H2)hold,and(φ,ψ,θ)is the solution of the problem (1.10)-(1.12) andf(x,t),z(x,t),h(x,t)∈C1([0,+∞),L2(0,1)). with constantsC′ >0,p>1,then there exists a constantC?>0 such that To achieve our results,we define a Lyapunov functionalL(t),and show that it is equivalent to the energy functionE(t). Lemma 4.7ForNsufficiently large,the functional defined by ProofIf we letL(t):=NE(t)+N1F1(t)+N2F2(t)+N3F3(t)+F4(t),then and then,we chooseε1small enough such that In this section,we shall establish the existence of uniform attractors for the system(1.10).SettingRτ=[τ,+∞),τ ≥0,we consider the following system Lemma 5.1[16]LetΣbe defined as before andF0∈Y,then whereγ,C1are two positive constants withC1>0 being independent of initial data.In the following,Cdenotes general positive constant,which may be different in different estimates. Obviously,we have The proof is complete. The main purpose of following part is to establish the uniformly asymptotic compactness(with respect toF ∈Σ).Without loss of generality,we deal with the strong solutions in the following part,then the case for weak solutions follows easily for a similar argument. Thus integrating (5.13) over [σ,T],we arrive at According to (5.11)-(5.12),we obtain Theorem 5.3Assume thatFsatisfies(5.3),then the family of semi-process{UF(t,τ)}(F ∈Σ,t ≥τ,τ ≥0),corresponding to (5.1),is uniformly (w.r.t.F ∈Σ) asymptotically compact inH1. ProofBecause the family of semi-process{UF(t,τ)}(F ∈Σ,t ≥τ,τ ≥0) has a bounded uniformly absorbing set,by the definition ofCM,we know that for any fixedε>0,we can chooseT >0 so large that Due to Lemma 5.1,it is sufficient to prove thatR(·,·,·,·,·)∈Contr(A0,Σ) for each fixedT.From the proof of Theorem 5.1,we can deduce that for any fixedT,we have Theorem 5.4Assume thatf,z,hsatisfies(5.3)andΣis defined above,then the family of processesUF(t,τ)(F ∈Σ,t ≥τ,τ ≥0)corresponding to(5.1)has a compact uniform(w.r.t.F ∈Σ) attractorAΣ. ProofAccording to Theorems 5.2 and 5.3,we have the existence of a uniform attractor at once.

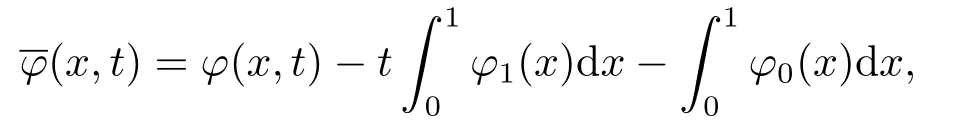

3.Global Well-Posedness of the Problem

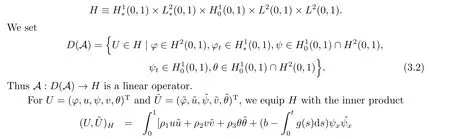
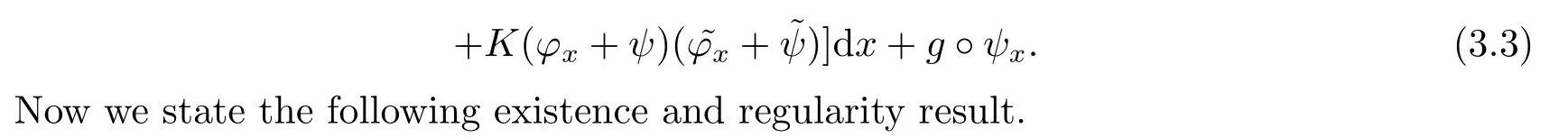


4.Uniform Stability


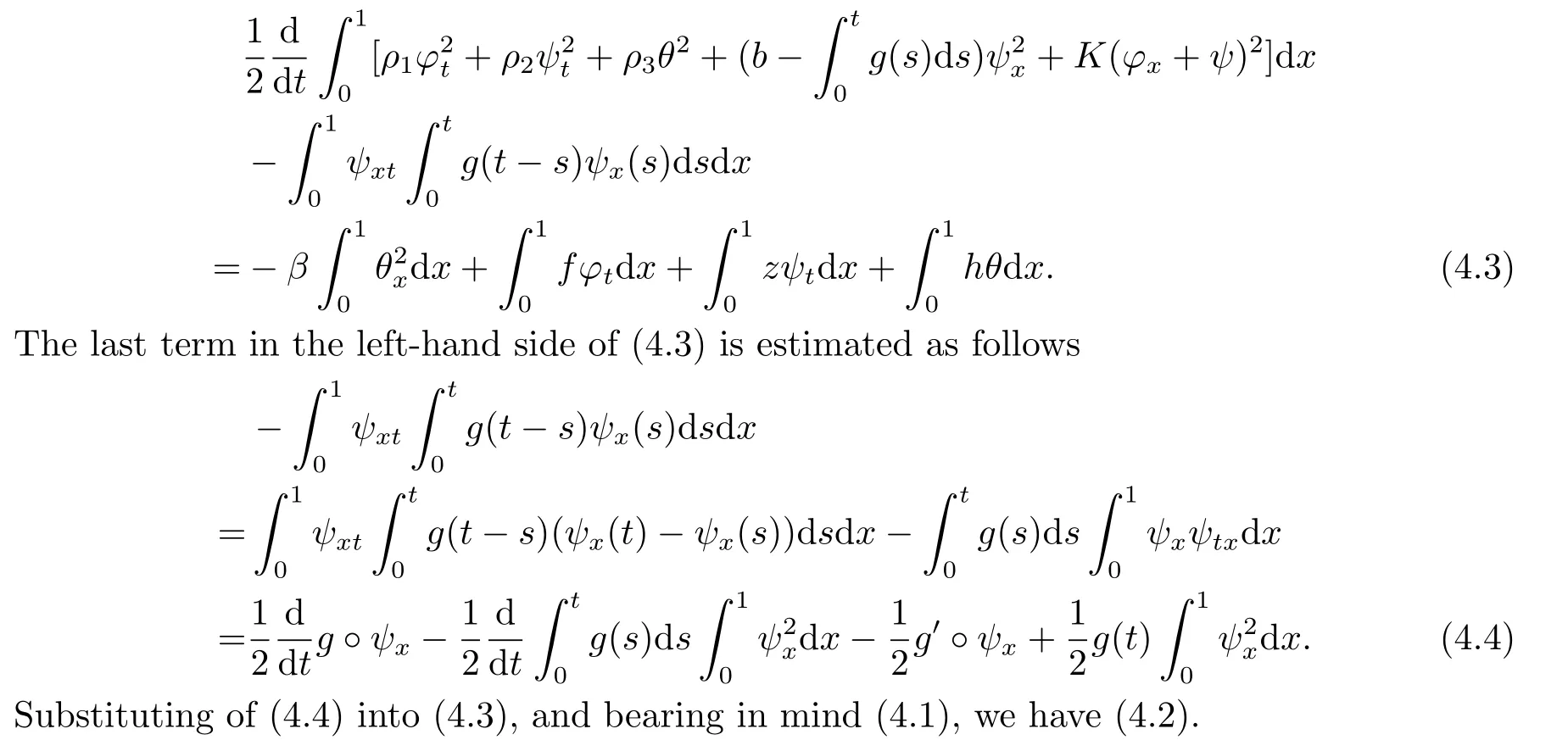

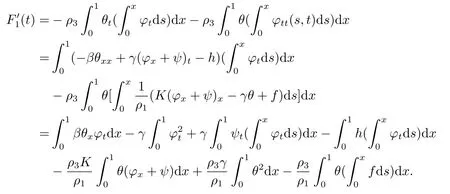
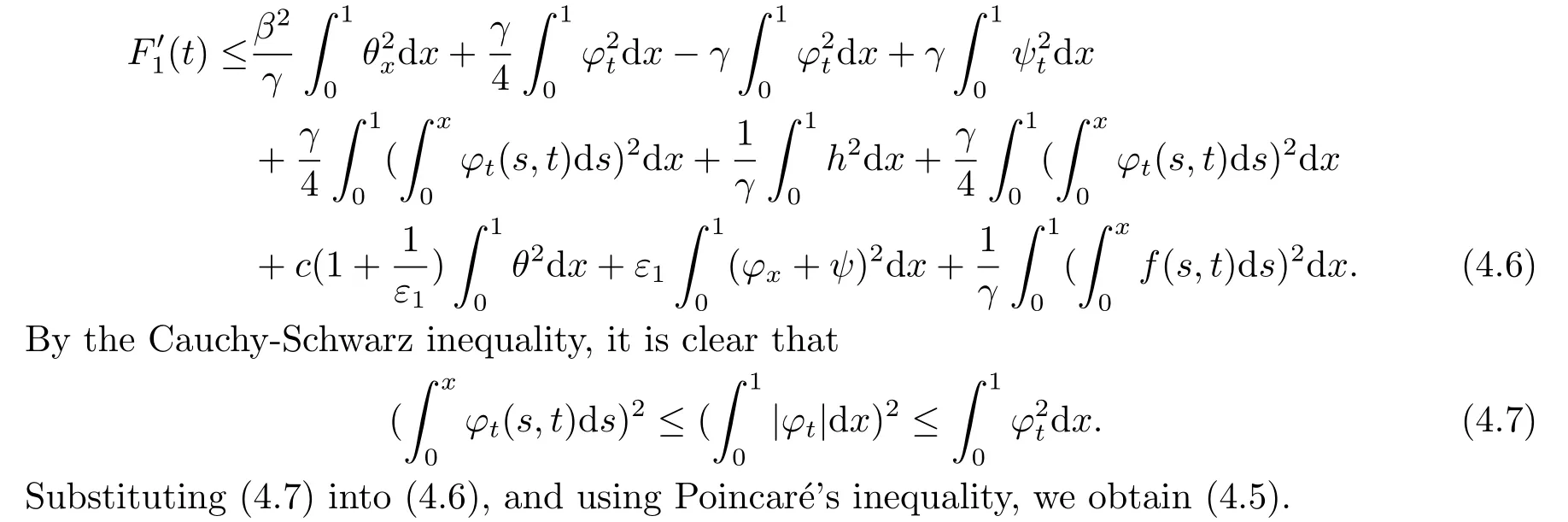
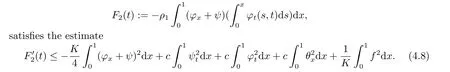
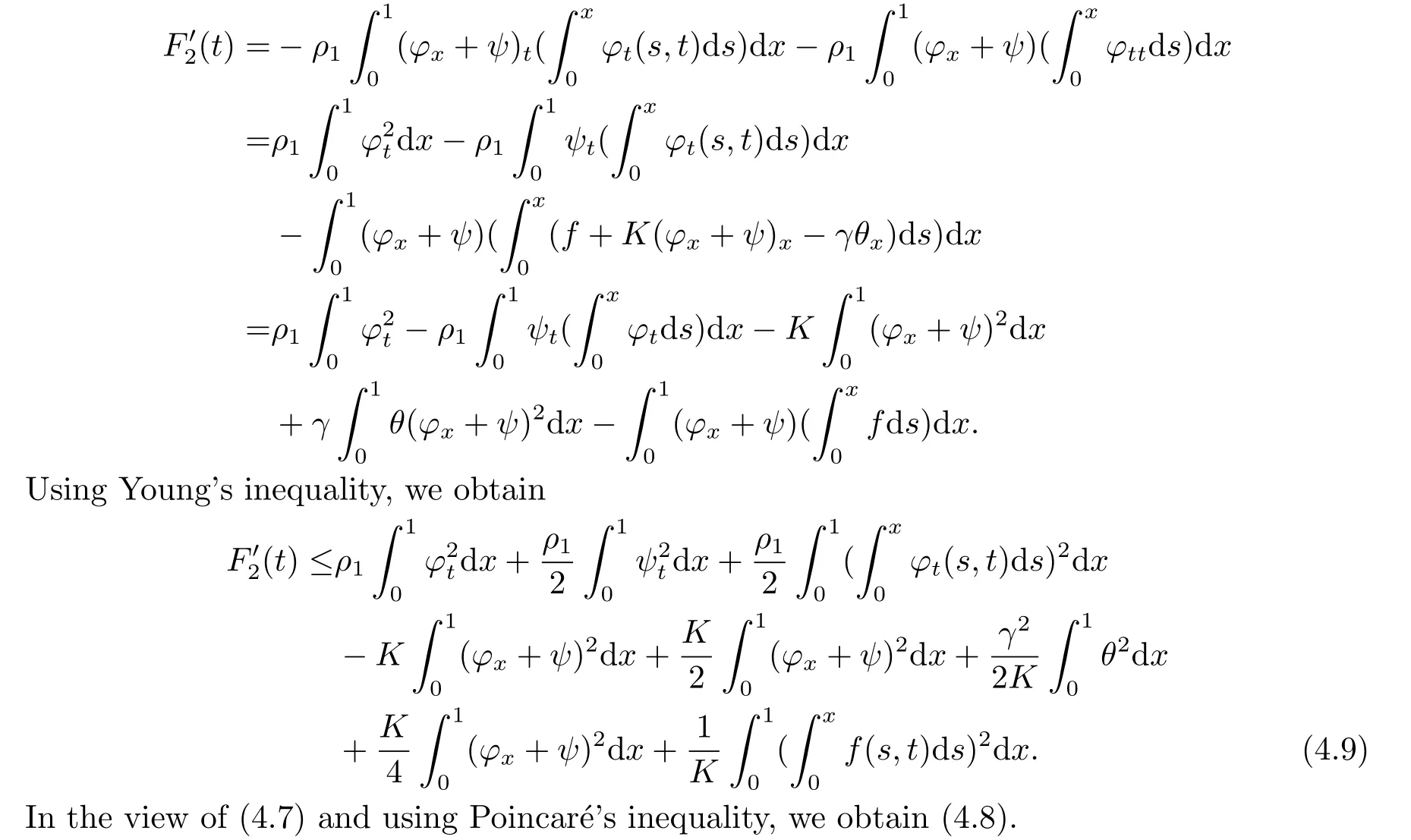
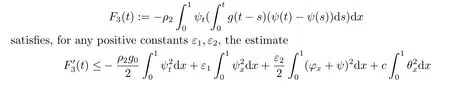
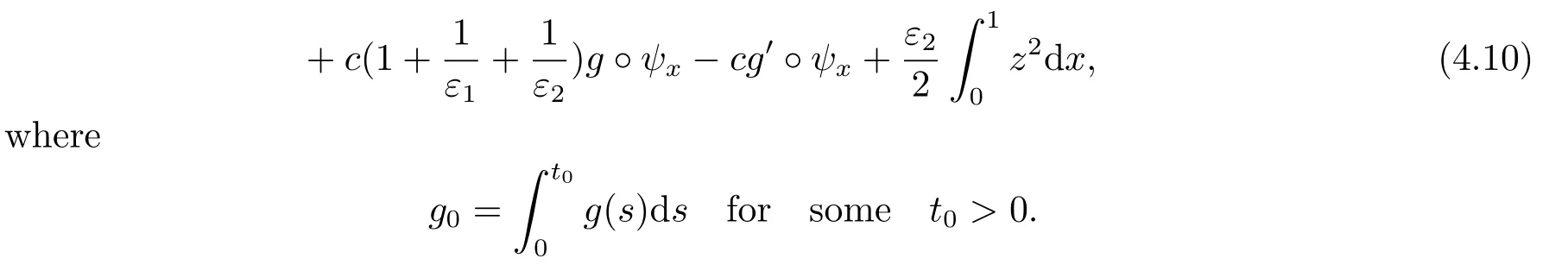

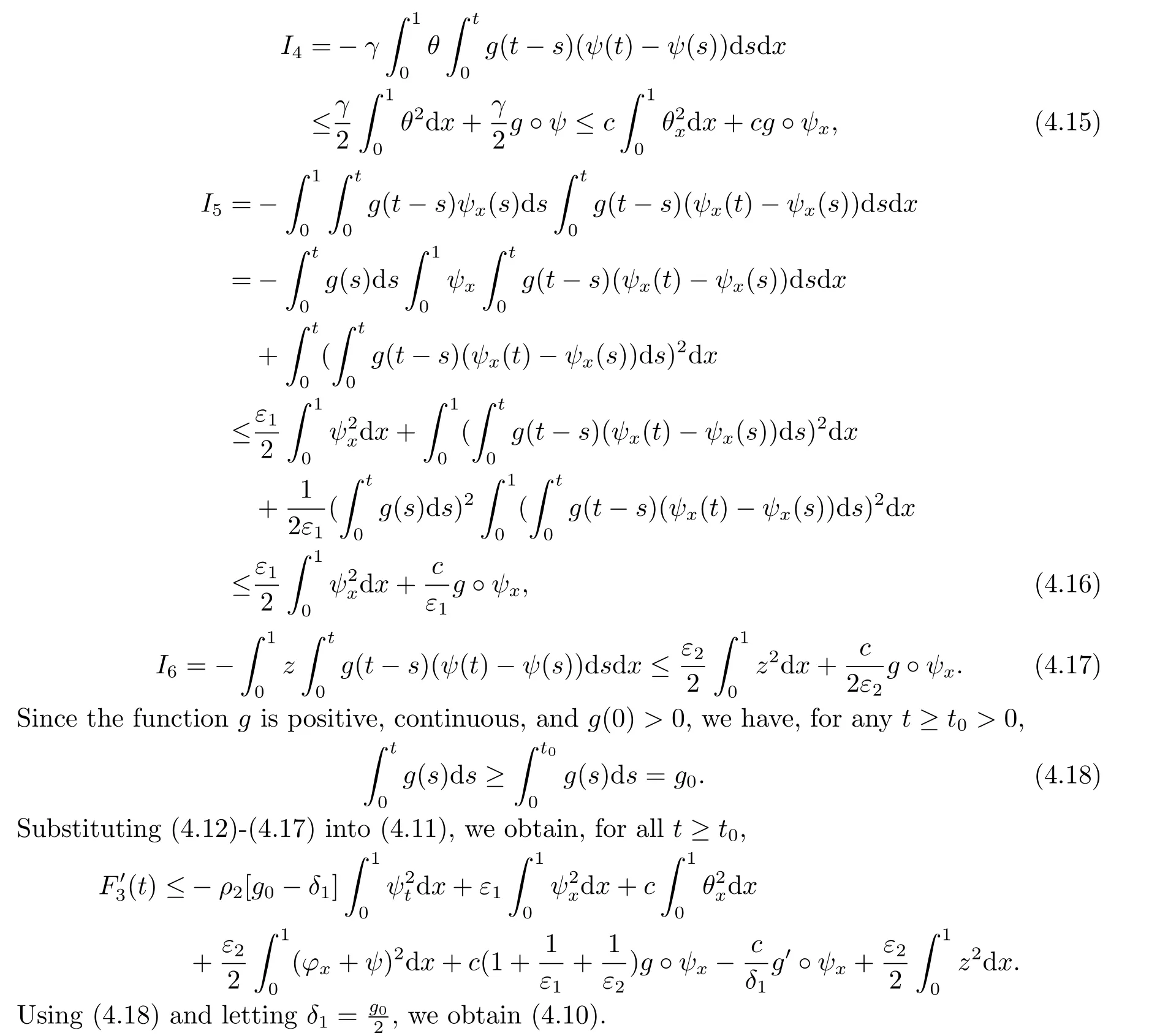
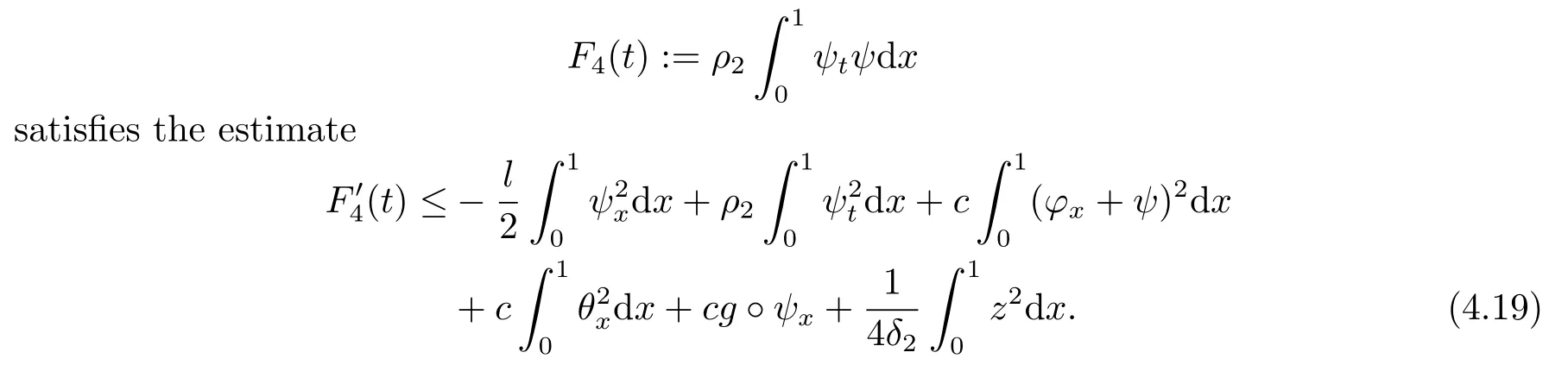
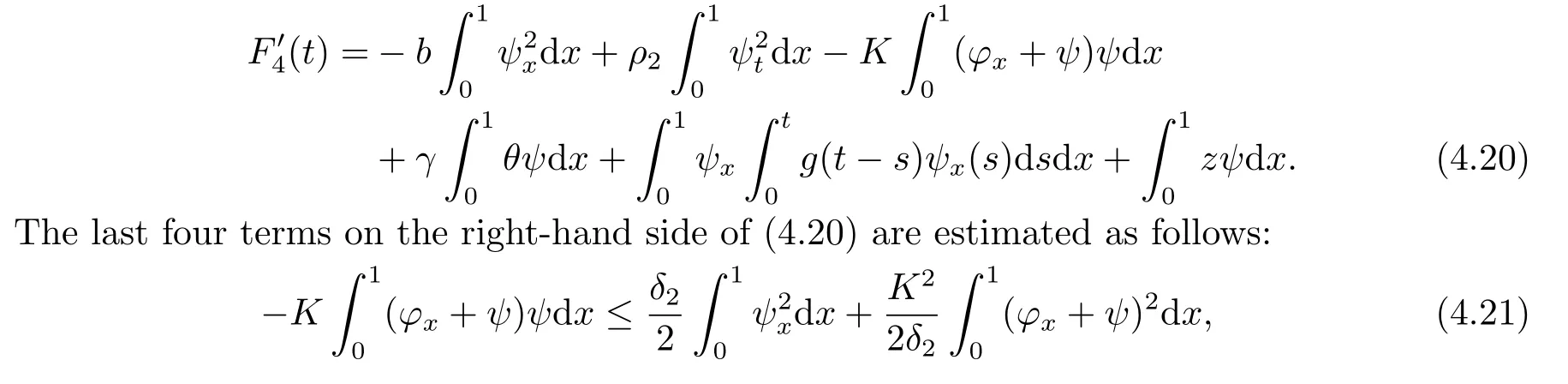
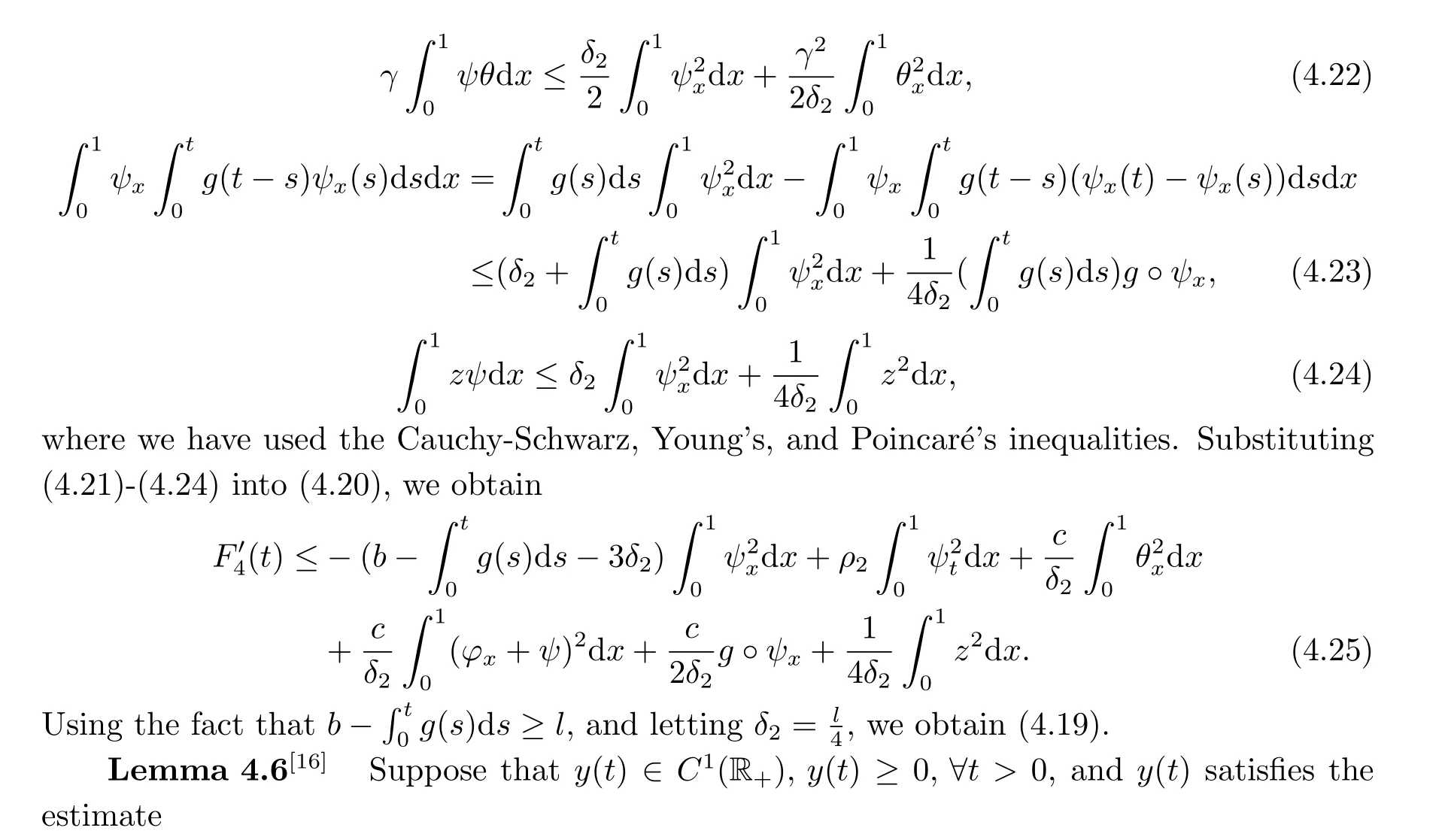
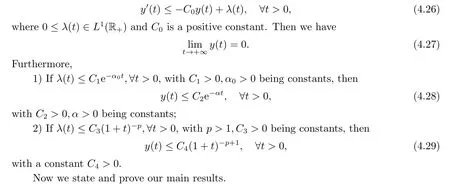
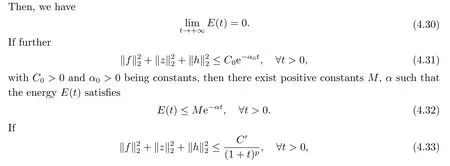
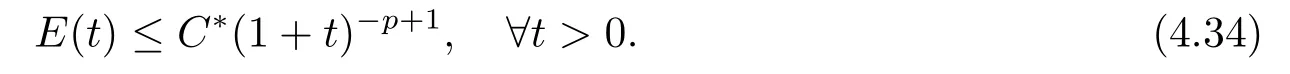
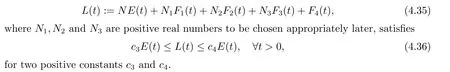
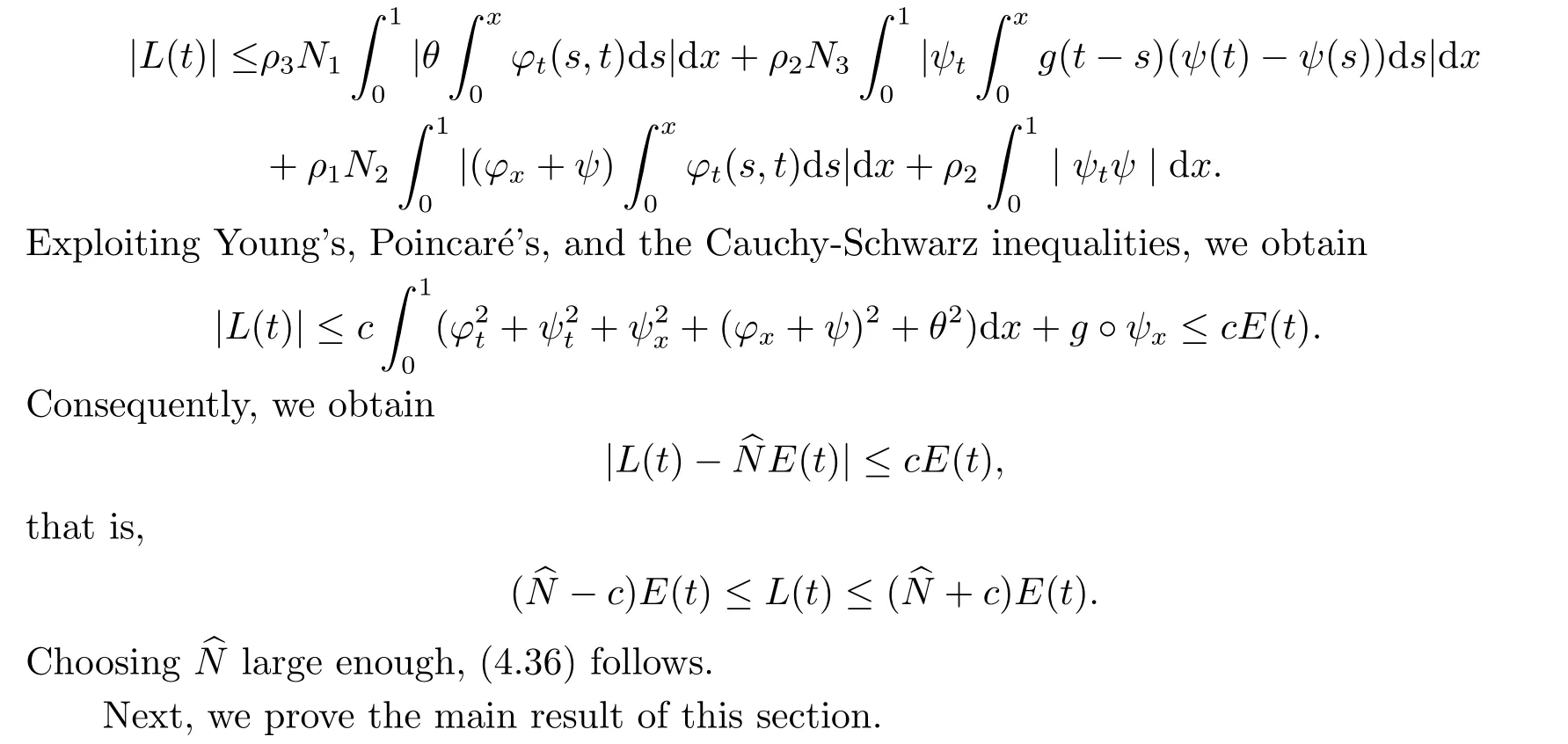


5.Uniform Attractors