基于PCA優(yōu)化的PSO-FCM聚類算法①
陳 誠,劉振宇
(南華大學(xué) 計(jì)算機(jī)科學(xué)與技術(shù)學(xué)院,衡陽 421001)
作為傳統(tǒng)聚類算法模糊C-均值聚類算法(Fuzzy C- Mean clustering algorithm,FCM)的一種優(yōu)化算法,引入了粒子群優(yōu)化算法(Particle Swam Optimization,PSO),粒子群模糊聚類算法(Particle Swarm-based Fuzzy Clustering algorithms,PSO-FCM),通過PSO 算法的收斂速度快,粒子收斂由自身最優(yōu)位置和群體最優(yōu)位置相結(jié)合,在一定程度上解決了FCM 對初始值敏感,對噪聲數(shù)據(jù)敏感,容易陷入局部最優(yōu)解的缺點(diǎn).如今,隨著數(shù)據(jù)量多樣化,復(fù)雜化,多類別化,PSOFCM 只是單一優(yōu)化初始聚類中心選取問題,沒有合理的限制粒子的移動,并不能更好優(yōu)化好FCM 算法面對多聚類問題時(shí)[1-7].
為了解決上述問題,引入主成分分析(Principal Component Analysis,PCA),本文提出基于PCA 優(yōu)化的粒子群模糊聚類算法(PCA-PSO-FCM),通過PCA 對數(shù)據(jù)各維度的分析和評定綜合給出一個權(quán)重值,粒子各維度會根據(jù)該調(diào)整權(quán)重速度和方向.本文詳細(xì)介紹了PCA-PSO-FCM,并且與FCM 和PSO-FCM 進(jìn)行了實(shí)驗(yàn)結(jié)果的比對,從實(shí)驗(yàn)上來看,本文的算法在多種群聚類問題上性能更好,是一種很有潛力的聚類算法.
本文結(jié)構(gòu)如下:第1 部分主要對已有的算法的研究成果進(jìn)行簡要分析總結(jié);第2 部分對于本文的優(yōu)化算法進(jìn)行詳細(xì)說明;第3 部分說明實(shí)驗(yàn)過程相關(guān)細(xì)節(jié),設(shè)定參數(shù)以及實(shí)驗(yàn)結(jié)果的分析;第4 部分總結(jié)全文.
1 算法介紹
PSO-FCM 算法是模糊均值聚類算法基礎(chǔ)上的優(yōu)化算法,傳統(tǒng)的模糊C 均值算法的結(jié)果精度,對初始中心的選取有很嚴(yán)格的要求,并且容易陷入局部最優(yōu)解.為了解決這個問題,國內(nèi)許多學(xué)者,利用具有集體智能的粒子群優(yōu)化算法,與傳統(tǒng)模糊C 均值算法結(jié)合.利用PSO 算法求解初始聚類中心,進(jìn)而優(yōu)化了FCM 依賴初始中心的問題;利用PSO 算法中,粒子個體與粒子群體之間關(guān)系,粒子整體移動的速度可以調(diào)節(jié),進(jìn)而降低了FCM 容易陷入最優(yōu)解的可能性.
1.1 PSO-FCM 算法
PSO-FCM 算法是基于數(shù)據(jù)樣本之間的模隸屬矩陣建立的聚類算法.算法的核心思想是:n個文本樣本為X=(x1,x2,···,xn),劃分為C =(c1,c2,···,cn),p個聚類中心,計(jì)算出每個文本的隸屬度 μij,μij表示第j個樣本隸屬于第i個樣本的隸屬度.

根據(jù)每個樣本的隸屬度值計(jì)算出適應(yīng)度函數(shù)值:

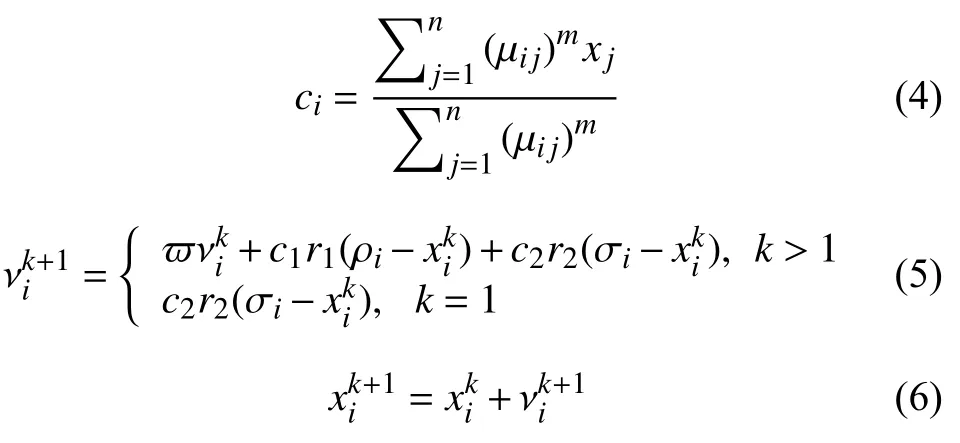
式中,m是加權(quán)指標(biāo),m>1,xj-νi表示樣本xj到第i個樣本中心的聚類,PSO-FCM 算法適應(yīng)度函數(shù)Jm值越小說明性能越好;ρi是粒子最優(yōu)適應(yīng)度的位置,σi是群體最優(yōu)適應(yīng)度函數(shù),c1和c2是 學(xué)習(xí)因子;r1和r2是[0,1]之間的隨機(jī)因子數(shù),?是慣性權(quán)重.
2 算法優(yōu)化
2.1 PCA 算法
隨著數(shù)據(jù)量的爆發(fā)和激增,數(shù)據(jù)類型的增多,數(shù)據(jù)復(fù)雜程度的加深,PSO-FCM 算法的性能無法完全發(fā)揮.于是近年來有學(xué)者對該算法進(jìn)行了再度優(yōu)化,陳壽文[8]提出利用混沌粒子融合粒子群模糊聚類算法(CCPSOFCM),余曉東等[9]利用直覺模糊核優(yōu)化粒子群模糊聚類算法.雷浩轄等[10]利用遺傳算法(GA)與PSO 混合優(yōu)化的遺傳粒子群模糊聚類(GA-PSO-FCM).這些學(xué)者都是針對于PSO-FCM 算法依賴初始解這個問題上進(jìn)行的優(yōu)化.算法核心是通過比較隸屬度,移動該粒子并決定屬于哪一類,但是在各維度上面的移動上并沒有一個主次之分,在各維度上的移動全部是隨機(jī)因子數(shù)決定.隨著聚類中心數(shù)量的增加,隸屬度矩陣上,各聚類中心隸屬度值接近,粒子各維度移動不受限,這樣導(dǎo)致部分粒子可能會被分入,與正確聚類中心隸屬度值接近的錯誤聚類中心中的問題.在維度增加,聚類中數(shù)量增加,這個問題會越來越頻繁出現(xiàn).
為了在一定程度降低上面的問題出現(xiàn)的可能性,本文引入了PCA[11-13]算法對原算法進(jìn)行優(yōu)化,PCA 是一種統(tǒng)計(jì)分析的方法,通過正交變換將具有一定相關(guān)性的向量轉(zhuǎn)為彼此正交,且互相獨(dú)立的一維新向量(即主成分).每個主成分都是初始變量的線性組合,沒有冗余信息,構(gòu)成空間的正交基.主成分分析法可以簡化統(tǒng)計(jì)數(shù)據(jù),揭示特征變量之間的關(guān)系.在本文優(yōu)化中并沒直接對數(shù)據(jù)進(jìn)行降維,根據(jù)PCA 中主成分貢獻(xiàn)率公式:計(jì)算出樣本空間各維度之間的貢獻(xiàn)率η=(η1,η2,···,ηn),進(jìn)一步優(yōu)化PSO-FCM 算法中速度的的迭代公式:
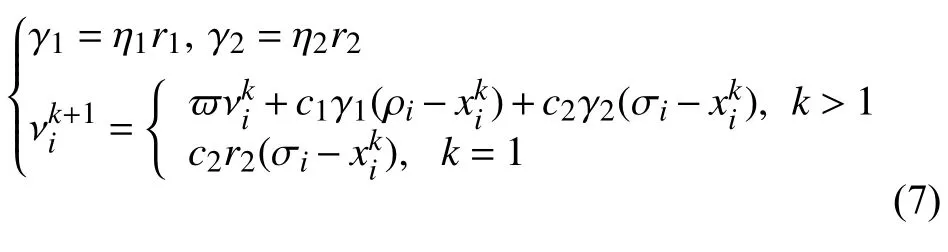
2.2 優(yōu)化算法實(shí)現(xiàn)

?

?
3 實(shí)驗(yàn)分析
3.1 實(shí)驗(yàn)數(shù)據(jù)處理
在測試算法的性能,本文選擇UCI 機(jī)器學(xué)習(xí)數(shù)據(jù)庫中,Wine,Breast Tissue,Dermatology,以及Glass Identification,每一組數(shù)據(jù)都進(jìn)行了清洗,并且都做了使用線性函數(shù)歸一化將數(shù)據(jù)集進(jìn)行標(biāo)準(zhǔn)化處理.各維度的權(quán)重是通過主成分分析得出各維度貢獻(xiàn)率,數(shù)據(jù)集參見表1 數(shù)據(jù)集表.

表1 實(shí)驗(yàn)數(shù)據(jù)集表
3.2 模型評價(jià)指標(biāo)
通過對比本算法與K-近鄰(KNN),FCM,PSO-FCM在數(shù)據(jù)集訓(xùn)練的結(jié)果.本文采取的評價(jià)算法性能的指標(biāo):調(diào)整互信息(Adjusted Mutual Information based scores,AMI);調(diào)整蘭德系數(shù)(Adjusted Rand Index,ARI);FM 指數(shù)(Fowlkes and Mallows Index,FMI).3 個指標(biāo)都是評價(jià)聚類算法性能的外部指標(biāo),通過聚類結(jié)果與參考數(shù)據(jù)集的標(biāo)簽比較而獲得,這些外部指標(biāo)度量的結(jié)果都在[0,1]之間,指標(biāo)值越接近1 說明聚類的結(jié)果越好.
3.3 檢驗(yàn)?zāi)P托阅?/h3>
圖1 和圖2 根據(jù)Breast Tissue 數(shù)據(jù)集的主成分貢獻(xiàn)率所選擇的平面圖,圖1 是本文算法在數(shù)據(jù)集上,兩個高貢獻(xiàn)率維度的圖像,圖2 是PSO-FCM 算法,從圖中可以明顯的對比出來,在相同數(shù)據(jù)集,相同維度下的本文算法聚類的結(jié)果明顯優(yōu)于PSO-FCM,PSO-FCM算法在數(shù)據(jù)比較集中的區(qū)域,對于多個聚類中心的交界處的數(shù)據(jù)敏感程度低,無法有效的給出數(shù)據(jù)的準(zhǔn)確的聚類中心,相反本文算法面對這類粒子,敏感度高,能夠更加有效的且準(zhǔn)確的給出聚類中心.粒子各維度之間無差別移動,在多個聚類中心的粒子會被錯誤的移動到不正確的聚類中心中:本算法對于不同貢獻(xiàn)率的空間中,采取相對應(yīng)的移動權(quán)重的能夠較低粒子錯誤移動的概率,說明該策略效果是顯著的.
由表2 和表3 中可以看出,本文算法只是在Dermatology 數(shù)據(jù)集上的AMI 這一個指標(biāo)上落后KNN,這是因?yàn)樽鳛橛簿垲愃惴?隨著聚類中心數(shù)目的增加,每一個數(shù)據(jù)只能存在單一的一個聚類結(jié)果,不會存在多種可能性,聚類的結(jié)果純度更高.KNN 算法性能很穩(wěn)定,在隨著聚類中心增多,性能反超F(xiàn)CM,PSO-FCM 兩個算法,但是綜合指標(biāo)上,本文的算法總體仍是優(yōu)于FCM,PSO-FCM,KNN 這3 個算法.FCM 采用隨機(jī)初始的中心,指標(biāo)隨著聚類中心的增多,算法性能下降明顯.PSOFCM 采取使用PSO 算法得出的初始中心,明顯的發(fā)現(xiàn),綜合性能上面性能上優(yōu)于FCM,但是算法精度提升不高.
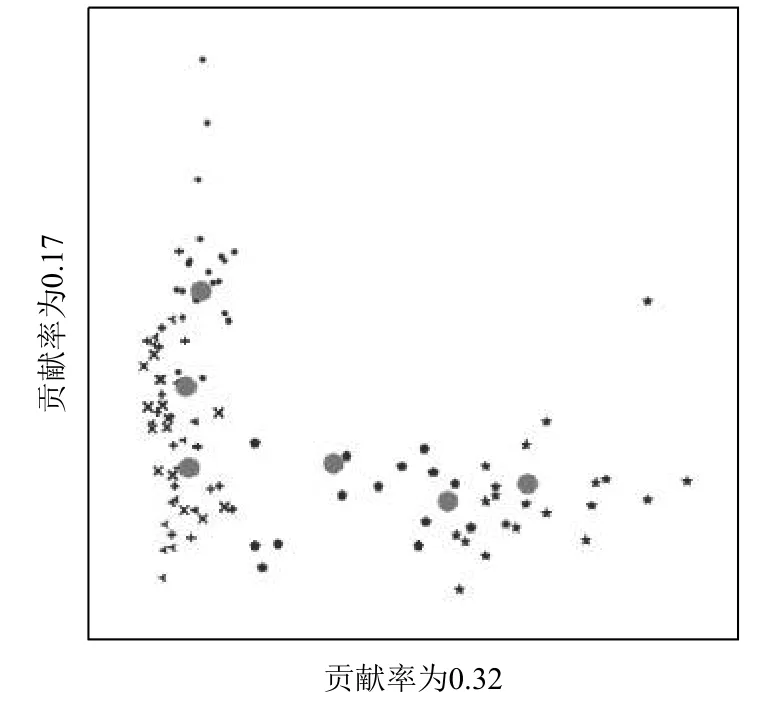
圖1 PCA-PSO-FCM 高貢獻(xiàn)率圖

圖2 PSO-FCM 高貢獻(xiàn)率圖
隨著各數(shù)據(jù)集的聚類中心的增加,聚類的問題的復(fù)雜化,從表中各指標(biāo)上,側(cè)面體現(xiàn)本算法面對多個聚類中心的之間的粒子敏感度更高,分辨能力更強(qiáng).總體上指標(biāo)上來看,本文算法性能更強(qiáng),魯棒性更高,適用面更廣.
4 結(jié)論與展望
采取PCA 優(yōu)化的PSO-FCM 算法,通過主貢獻(xiàn)率加權(quán)的限制,控制粒子各維度上的移動,降低多聚類群交界粒子的敏感性,增強(qiáng)了粒子的搜索能力,降低粒子被不正確粒子群吸入,能夠一定程度上,跳出局部最優(yōu),有效的彌補(bǔ)了傳統(tǒng)PSO-FCM 性能上的不足,增加算法精度,增強(qiáng)算法的魯棒性,相對于其他算法,在綜合指標(biāo)上面更優(yōu),部分指標(biāo)上有著更好的精度,適用面更廣,魯棒性更強(qiáng).接下來的工作會將優(yōu)化算法應(yīng)用到更多領(lǐng)域.

表2 算法性能表1

表3 算法性能表2

