LEONARD PAIRS CONSTRUCTED FROM THE QUANTUM ALGEBRA νq(sl2)
LIU Jun-li, XU Qiu-li, JIANG Wei
(College of Science, Langfang Normal University, Langfang 065000, China)
Abstract: In this paper, we study the construction of Leonard pairs.By using the finite dimensional irreducible representations of quantum algebra νq(sl2), we get Leonard pairs, and give the classification of Leonard pairs, which provide more help in studying Leonard triples.
Keywords: Leonard pair; quantum algebra; irreducible representation; split basis
1 Intro duction
Leonard pairs were introduced by Terwilliger in [1], which gave some examples to illustrate how Leonard pairs arise in representation theory, combinatorics, and the theory of orthogonal polynomials.Because these polynomials frequently arise in connection with the finite-dimensional representations of good Lie algebras and quantum groups, it is natural to find Leonard pairs associated with these algebraic objects.Leonard pairs of Krawtchouk type were described in [2]using split basis and normalized semisimple generators ofsl2.Leonard pairs ofq-Krawtchouk type were described in [3]using split basis ofUq(sl2).Recently,Alnajjar and Curtin in[4]gave general construction of Leonard pairs of Racah,Hahn,dual Hahn and Krawtchouk type using equitable basis ofsl2.Alnajjar in [5, 6]gave general construction of Leonard pairs ofq-Racah,q-Hahn, dualq-Hahn,q-Krawtchouk, dualq-Krawtchouk, quantumq-Krawtchouk, and affineq-Krawtchouk type using equitable generators ofUq(sl2).The Leonard pairs and Leonard triples ofq-Racah type from the quantum algebraUq(sl2)were also discussed by Hou in[7]and[8].Equivalent presentations forUq(sl2)were introduced in [9].
Given a Leonard pair it is often more natural to work with a split basis rather than a standard basis.In this paper, we illustrate this with an example based on the quantum algebraνq(sl2).LetMdenote a finite-dimensional irreducibleνq(sl2)-module and assume A (resp.B) is an arbitrary linear combination ofF,K(resp.EH?1,H?1).We give the necessary and sufficient conditions on the coefficients for A,B to act onMas a Leonard pair.
The rest of this paper are organized as follows.In Section 2, we introduce some facts concerning the Leonard pairs.In Section 3, we recall some facts concerning irreducible finite-dimensionalνq(sl2)-modules.In Section 4, we define two linear transformations A and B using the elements inνq(sl2) and describe their properties.At last, we characterize when the pair A,B is a Leonard pair.
2 Leonard Pairs
In this section,we recall the definitions and some related facts concerning Leonard pairs,and more details about the Leonard pairs can be found in [3].Throughout this paperFdenotes an algebraically closed field.Fix a nonzero scalarq ∈Fwhich is not a root of unity.Md+1(F) denote theF-algebra consisting of all (d+1) by (d+1) matrices having rows and columns indexed by 0,1,2,···,dfor a nonnegative integerd.
LetVdenote aF-vector space of dimensionsd+1.Let End(V) denote theF-algebra consisting of all linear transformations fromVtoV.Letdenote a basis forV.For A∈End(V) andX ∈Md+1(F), we sayXrepresents A with respect towheneverwhereXijis the element in the matrixX.
A square matrix is said to be tridiagonal if each nonzero entry lies on either the diagonal,the subdiagonal, or the superdiagonal.A tridiagonal matrix is said to be irreducible if each entry on the subdiagonal is nonzero and each entry on the superdiagonal is nonzero.We now define a Leonard pair.
Definition 2.1LetVbe a vector space overFwith finite positive dimensions.A Leonard pair onVis an ordered pair of linear transformations A:V →Vand A?:V →Vthat satisfy both the conditions below.
(1) There exists a basis forVwith respect to which the matrix representingAis diagonal and the matrix representingA?is irreducible tridiagonal.
(2) There exists a basis forVwith respect to which the matrix representingA?is diagonal and the matrix representingAis irreducible tridiagonal.
There are so many examples of Leonard pairs which arise in representation theory,combinatorics, and the theory of orthogonal polynomials, for details can be found in [3].
Given a Leonard pair A,A?, it is natural to represent one of A,A?by an irreducible tridiagonal matrix and the other by a diagonal matrix.In order to distinguish the two representations, Terwilliger introduced the standard basis and split basis for this pair in [3].A square matrix is said to be lower bidiagonal whenever every nonzero entry lies on either the diagonal or the subdiagonal.A lower bidiagonal is said to be irreducible lower bidiagonal whenever each entry on the subdiagonal is nonzero.A matrix is upper bidiagonal (resp.irreducible upper bidiagonal) whenever its transpose is lower bidiagonal (resp.irreducible lower bidiagonal).
Definition 2.2LetVdenote a vector space overFwith finite positive dimension and let A,A?denote a Leonard pair onV.A standard basis for this pair is a basis forVwith respect to which the matrix representing A is irreducible tridiagonal and the matrix representing A?is diagonal.
Definition 2.3LetVdenote a vector space overFwith finite positive dimension and let A,A?denote a Leonard pair onV.A split basis for this pair is a basis forVwith respect to which the matrix representing A is irreducible lower bidiagonal and the matrix representing A?is irreducible upper bidiagonal.
The following theorem in [3]provides a way to recognize a Leonard pair.
Theorem 2.4(see [3]) LetVdenote a vector space overFwith finite positive dimension.Let A :Vand B :Vdenote linear transformations.Let us assume there exists a basis forVwith respect to which the matrices representing A and B have the following form
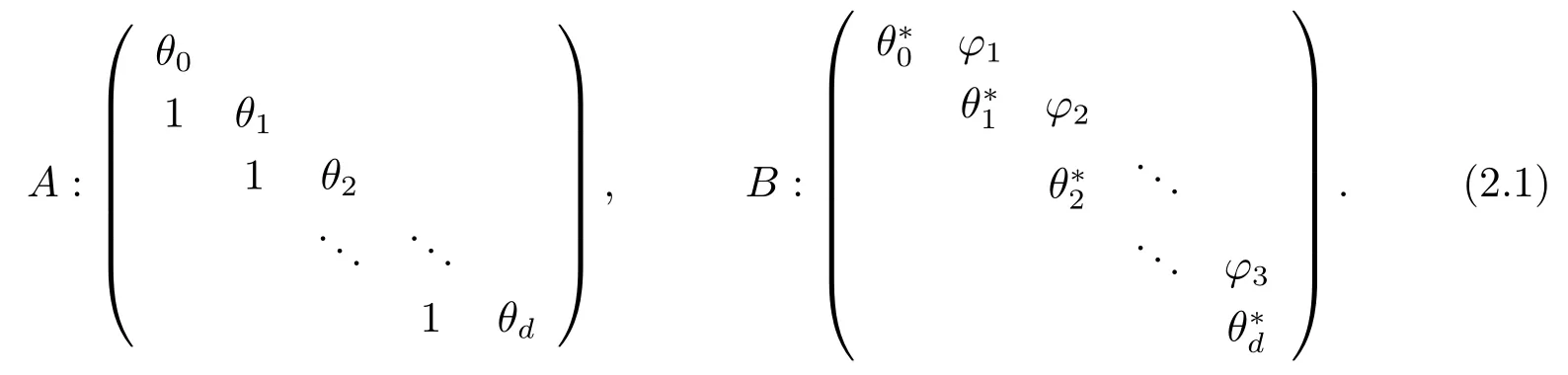
Then the pair A,B is a Leonard pair onVif and only if there exist scalarsφi(1≤i ≤d) inFsuch that conditions (i)–(v) hold below
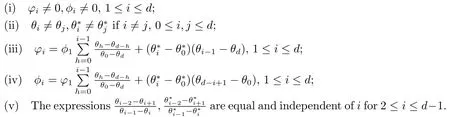
In the rest of this paper, we use the theorem to get Leonard pairs.
3 νq(sl2)-Modules
In this section, we recall some facts concerning irreducible finite-dimensionalνq(sl2)-modules in [10].
Definition 3.1The quantum algebraνq(sl2)is defined as the associative algebra(with 1 and overF) with the generatorsE,F,K,K?1,H,H?1and the following relations
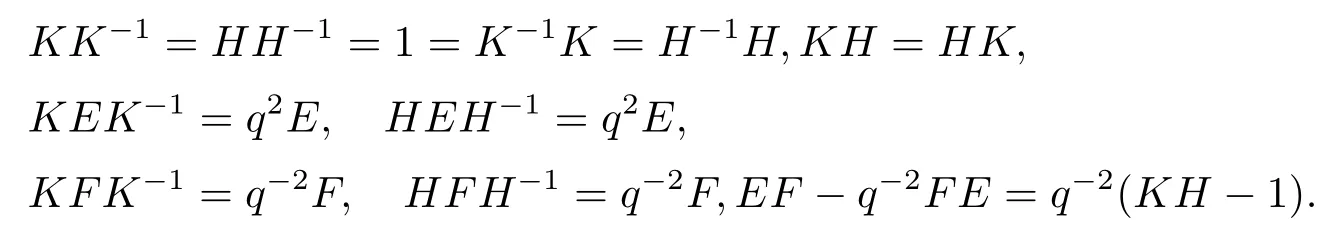
Lemma 3.2Lett ≥1 be an integer.Then we have the following formulas inνq(sl2),
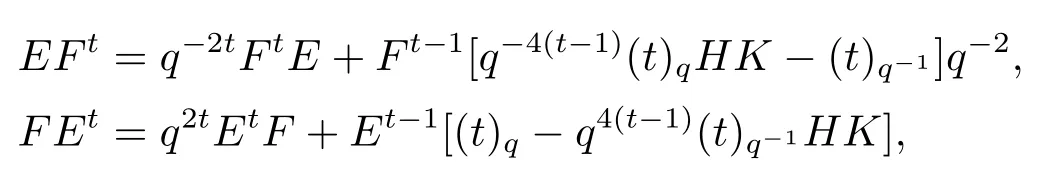
where (t)q=1+q2+···+q2(t?1).
Lemma 3.3Given an nonnegtative integernanda,b ∈Fwithab=q2n.LetMbe an+1-dimensional vector space with basis{m0,m1,···,mn}.We define theνq(sl2)-action onMas follows
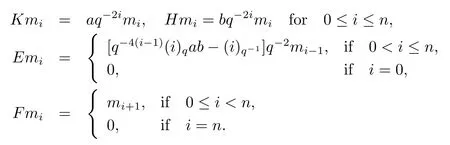
ThenMbecomes aνq(sl2)-module, we denote byM(n,a,b).
Theorem 3.4Suppose that V is a finite dimensional irreducibleνq(sl2)-module with dimensionn+1, thenVis isomorphic toM(n,a,b) for somea,b ∈Fwithab=q2n.
We describe the construction of Leonard pairs fromνq(sl2)-modules by using generators ofνq(sl2) in the next section.
4 Leonard Pairs From νq(sl2)
In this section, we define two linear transformations A and B of elements inνq(sl2) and characterize when the pair A,B is a Leonard pair.
Definition 4.1Referring to Definition 3.1 and Lemma 3.3 , letα,βdenote nonzero scalars inF.Then define two linear transformations A,B as follows
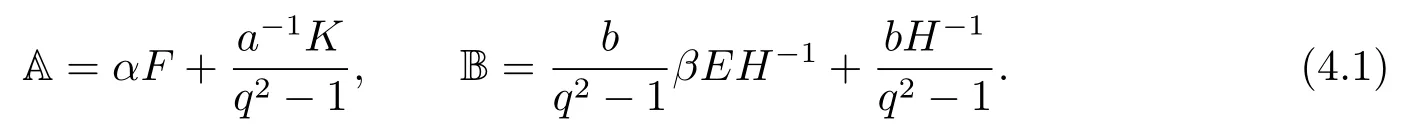
Now we give the main result in this paper.
Theorem 4.2Letnbe an nonnegative integer anda,b ∈Fwithab=q2n.Then the pair A,B defined in (4.1) acts onM(n,a,b) as a Leonard pair providedαβis not amongq?2,q?4···,q?2n.
To prove the above theorem, we apply Theorem 2.4.Before do this, we first give some lemmas.
Lemma 4.3There exists a basis forM(n,a,b) with respect to which the matrices representing A, B have the form of (2.1).
ProofWe can obtain this basis by modifying the basis{m0,m1,···,mn} given in Lemma 3.3.For 0≤i ≤n, we defineui=αimi.We observe{u0,u1,···,un} is a basis forM(n,a,b).The elementsE,F,K,Hact on this basis as follows
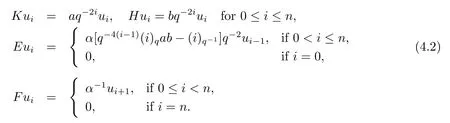
Takeab=q2ninto (4.2), we can get the coefficient ofui?1as below
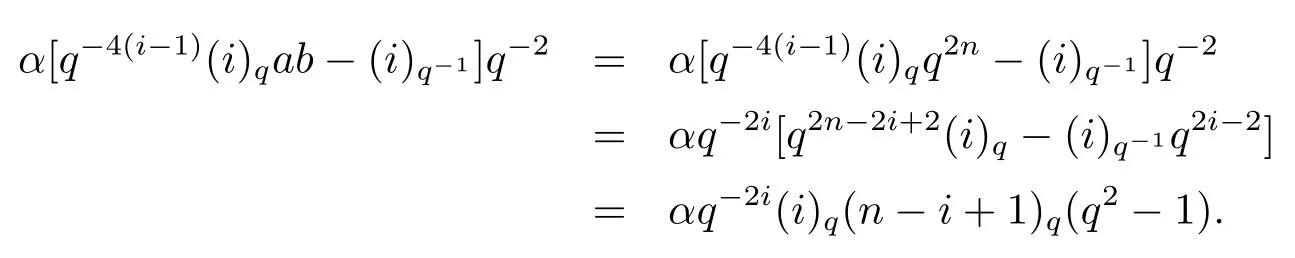
Using these comments we can get
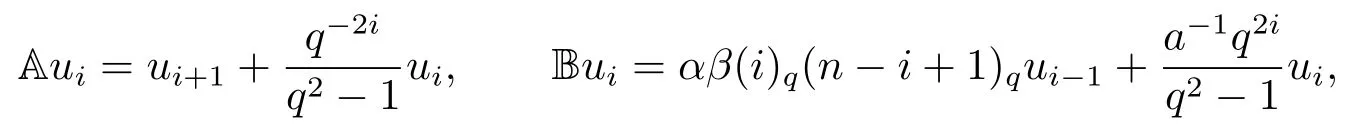
whereu?1=un+1= 0.Thus, with respect to the basis{u0,u1,···,un} the matrices representing A, B are given in (2.1), where
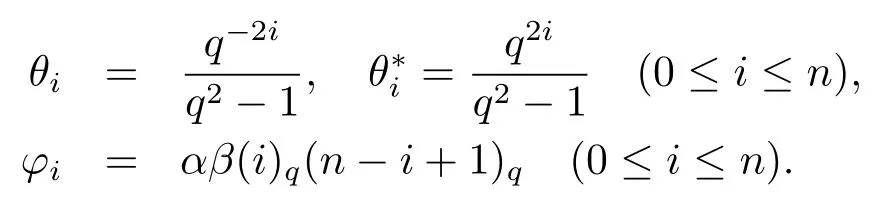
Lemma 4.4Referring to Lemma 4.3, the following two equations hold
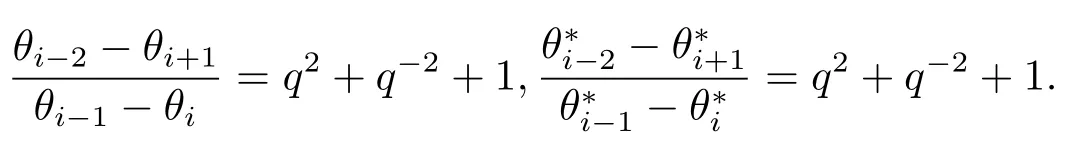
ProofImmediate from Lemma 4.3 and a simple calculation.
Lemma 4.5Referring to Lemma 4.3, the scalarsθialso satisfy the following equation
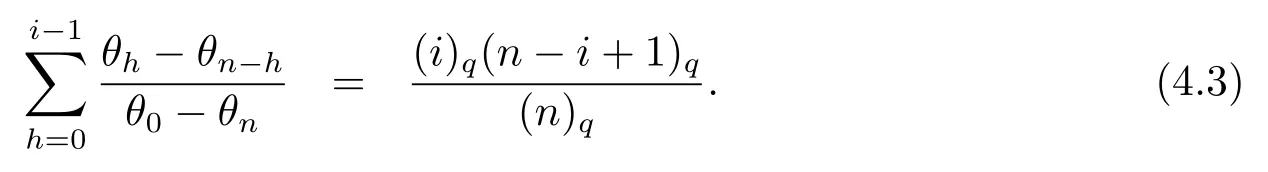
ProofUsing the sum of the geometric progression, we have

Then from (4.4), equation (4.3) holds.
Proof of Theorem 4.1Defineφi=(i)q(n ?i+1)q(αβ ?q?2(n?i+1)),1≤i ≤n.Let us assumeαβis not amongq?2,q?4···,q?2n.Then the above scalarssatisfy conditions (i)–(v) of Theorem 2.4 by Lemmas 4.3, 4.4 and 4.5.
Remark 1Applying Theorem 2.4 we find the pair A, B acts onM(n,a,b) as a Leonard pair.With respect to the basis{u0,u1,···,un}, the matrix representing A (resp.B) is irreducible lower bidiagonal (resp.irreducible upper bidiagonal).Therefore this basis is a split basis for A, B in view of Definition 2.3.
Remark 2By the classification of Leonard pairs in [11], those with=q2+q?2+1 are the familiesq-Racah,q-Hahn,dualq-Hahn,quantumq-Krawtchouk,affineq-Krawtchouk,q-Krawtchouk,or dualq-Krawtchouk,and since the pair A,B has this property(see Lemma 4.4), it’s easy to show that this pair is of quantumq-Krawtchouk type.

