Orthonormality of Volkov Solutions and the Sufficient Condition?
Hao Wang (王淏),Ming Zhong (鐘鳴), and Long-Fei Gan (甘龍飛)
Department of Physics,National University of Defense Technology,Changsha 410073,China
Abstract We present a simple demonstration on the orthonormality of Volkov solutions with emphasizing on the sufficient condition to the orthonormality.Properly aligning the external electromagnetic wave along the third-axis,the Volkov solutions are eigenfunctions of the hermitian momentump1, ?p2 and the light-cone hamiltonian operators with real eigenvalues,which can lead to a verification of the orthonormality in the context of quantum mechanics when the x3-integration of the external potential is not singularity as severe as δ(0).The hermiticity of the fermion field fourmomentum operators validates the application of the demonstration to the intense field quantum electrodynamic.The proof based on a direct calculation to the inner products of the solutions is recapitulated as well in a general manner without dependence on explicit representation of the Dirac matrices and spinors,which can be conducive to understand the sufficient condition and to the study of the polarized electron production where a convenient representation is selected elaborately to project out the spin-polarization.
Key words: Volkov solutions,orthonormality,intense field QED
1 Introduction
As prototype solutions of the Dirac equation in timevariant external fields,the Volkov functions are of significance in exploring the strong field physics.[1]The analytical functions have experienced an extensive range of applications in quantum mechanics (QM) and intense field quantum electrodynamic (IFQED) to describe the fermions in strong plain wave electromagnetic field environments since the pioneer works.[2?7]The collected data in the first experimental study on the interaction of high energy electron and the intense laser exploited at SLAC was analysed in terms of the functions.[8?10]From then on a surge of studies based on the functions were carried out.[11?53]Furthermore,the functions facilitate in paving the way to the analytical solutions of the equation in a more general background electromagnetic field.[54?55]
The orthonormality is one of the most concerned properties of the Volkov functions.It was used more or less explicitly in many phenomenological calculations,such as the cross sections or production rates,the time evolution of a free electron wave packet in a laser beamet al.,[56]The orthonormality is crucial to the consistence of quantum theories.In QM the Volkov solutions are the wave functions of the fermions.The question of orthogonality determines if we can build a sensible theory since the non-orthogonality will result in the non-hermit of the momentum and the Dirac hamiltonian operators,and ultimately ruin the unitarity of the theory,[57?58]while in IFQED,the Dirac field is expanded in terms of the Volkov functions with the coefficient operators relating to annihilating electron and creating positron respectively.[59]The non-orthogonality might lead to the risk of breaking the electric charge conservation.
Given the significance,many efforts have been paid to the orthonormality from time to time.The doubt of orthonormality arose due to the observation that the solutions are not eigenfunctions of the Dirac Hamiltonian.[57?58]A direct calculation on the inner products of the functions by expressing them in the light-cone coordinate and in a specific representation of the Dirac matrices and the spinors was made to demonstrate the orthonormality in Refs.[60–61].The proof was extended to arbitrary space-time dimensions for the case of an external constant plus plane-wave field.[62]Assuming continuous differentiability of the electromagnetic vector potential,boundedness of its derivative and hermiticity of the hamiltonian operators,it was shown in Ref.[63] that regular wave packets which decay rapidly in spatial space can be constructed by superposition of the Volkov functions in the momentum space.The norm of a wave packet is identical to that of its corresponding momentum distribution,which presents an implicit interpretation of the orthogonality to the functions.The orthonormality at a fixed time of the functions is proved in a recent article,[64]relying on a geometric argument based on the Gauss theorem in four dimensions and the periodic boundary condition assumption on the solutions.The assumptions underlying these proofs are different.It is obvious that not all of them,acting as conditions,are physically necessary to the orthonormality.
We revisit the orthonormality of Volkov functions in this paper with emphasis on the extent to which the orthonormality can be achieved.It will be shown in an explicit and concise demonstration that the spaceintegration of external electromagnetic vector potential can not be singularities as severe as delta functions though the potential allows various poles at certain values of space and time.This is the least-constrained sufficient condition to the orthonormality and can be meet easily in applications.We start by presenting the representationindependent demonstration on the orthonormality in terms of a eigenfunctions method in Sec.2.Properly aligning the external electromagnetic wave along the third-axis,the Volkov functions are eigenfunctions of the momentum operators,and the light-cone hamiltonian operator,whereis the Dirac hamiltonian,with real eigenvalues in the context of QM.As corresponding to physical observables,the operatorsandare hermitian,which implies a derivation to the orthonormality of the Volkov functions when thex3-integration of the external potential is not singularity as severe asδ(0).By analyzing the hermiticity of the four-momentum operatorsPμof the fermion field theory,we show that the demonstration is also valid in IFQED.Since the solutions are exclusively applied in QM and IFQED,the demonstration is self-contained in physics.To test the sufficient condition,a direct proof of the orthonormality following the work in the light-cone coordinate[61]is recapitulated in Sec.3.The inner products of the solutions are calculated in a detailed and general manner without dependence on the explicit representation of the Dirac matrices and the spinors.To our knowledge the representation-independent calculation has not been available in the literatures and can serve as a rigorous supplement to the existed direct proof.[61,65?66]Moreover,such a proof can be conducive to the study of the polarized electron production,[67]in which a convenient representation to project out the spinpolarization can be made sense.A summary is made in Sec.4.
2 Volkov Solutions as Eigenfunctions and the Orthonormality
Analytically solving the Dirac equation in intense electromagnetic background
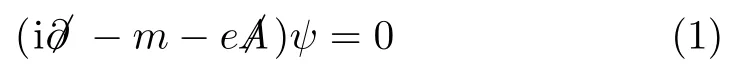
is of significance in exploring the intense field phenomenology.The most interesting and frequent-used solution at present was solved for the plain wave electromagnetic background in the Lorentz gauge?μAμ(η)=0.[1]The positive and negative frequency Volkov functions are
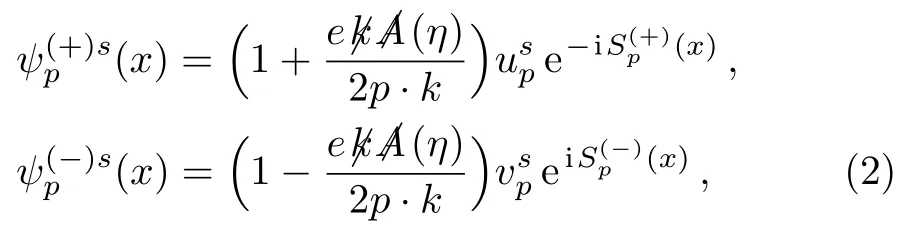
withkμthe external electromagnetic wave vector,η=k·xand
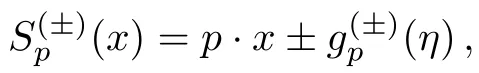
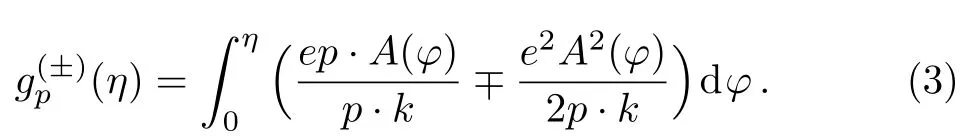
Theandare understood to have
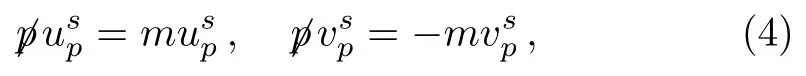
implyingp2=m2,and the orthonormalization
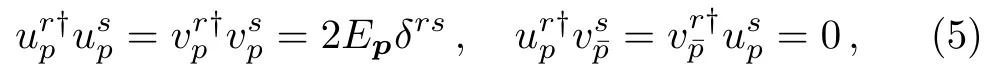
The spacetime derivatives of the Volkov functions are
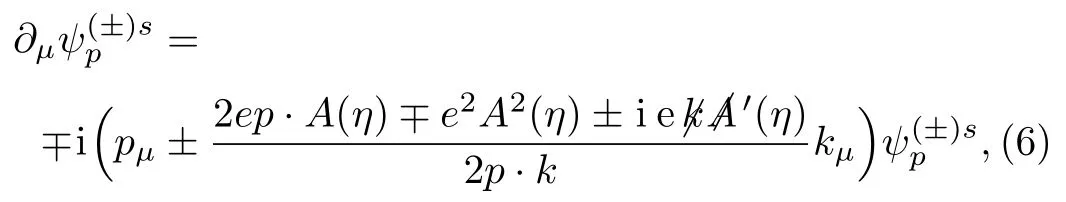
with

Observing in the reference frame where the external plane wave propagates along the third-axis,we havekμ=(k,0,0,k) andAμ=(0,A1,A2,0).Then we obtain the following eigenequations for the Volkov functions
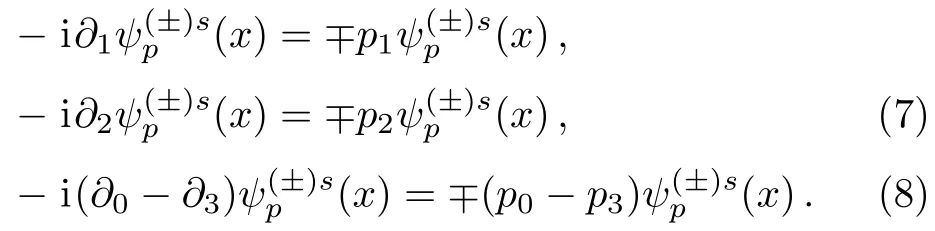
Using Eq.(1),we can alternatively write Eq.(8) as
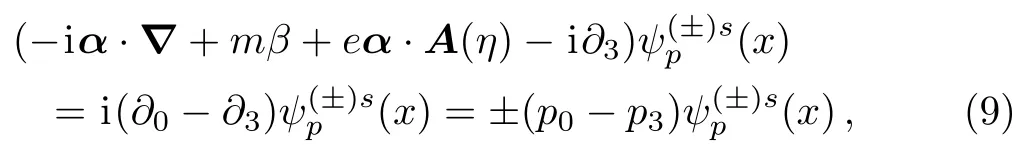
whereβ=γ0andα=γ0γare the Dirac matrices.Defining the momentum,Dirac and the light-cone hamiltonian operators
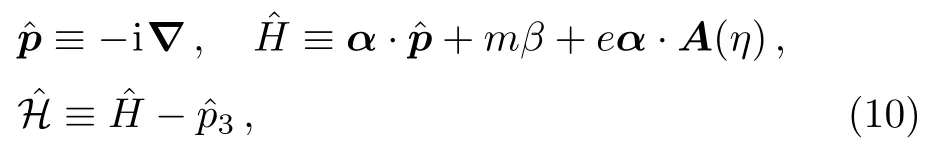
then the Volkov functions are the common eigenfunctions of the operators with real continuous eigenvalues
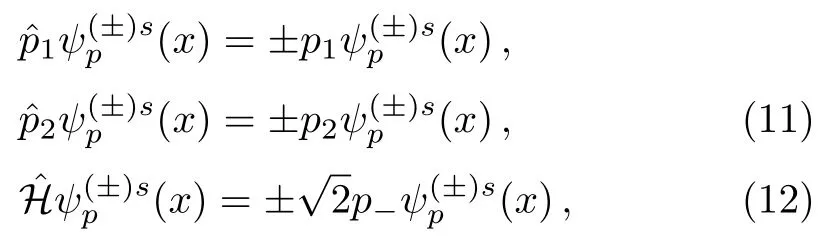
whereNote that the convention used is
As corresponding to the physical observables,the operators(i=1,2,3) andmust be hermitian in QM.The eigenfunctions belonging to different eigenvalues are orthogonal.The inner products of the Volkov functions can then be written as
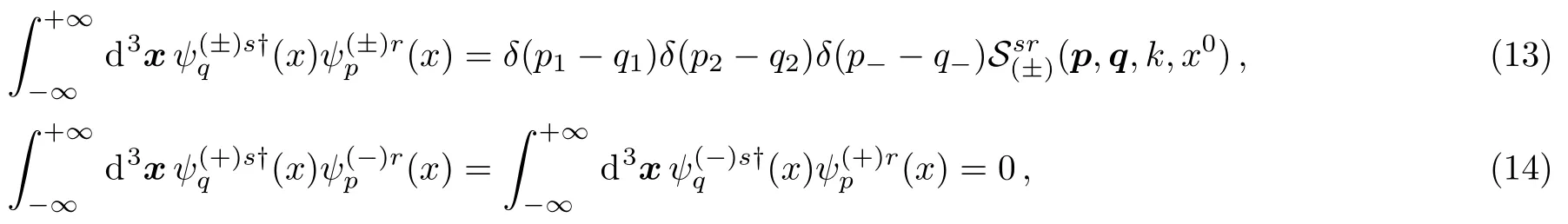
Usingp2=q2=m2,one can easily findwhenp1=q1andp2=q2.Then Eq.(13) becomes
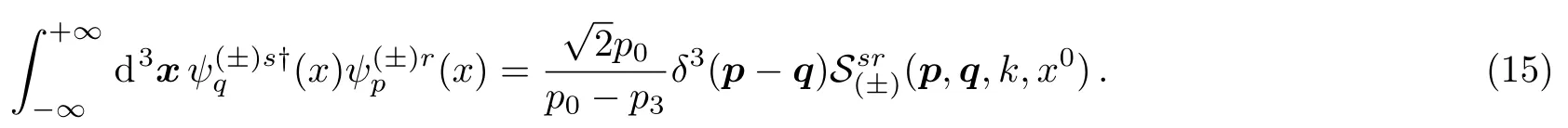
To determine thefactors,we substitute the explicit expression of the Volkov functions (2) to the left-handside of the above equation and evaluate it atp=q,
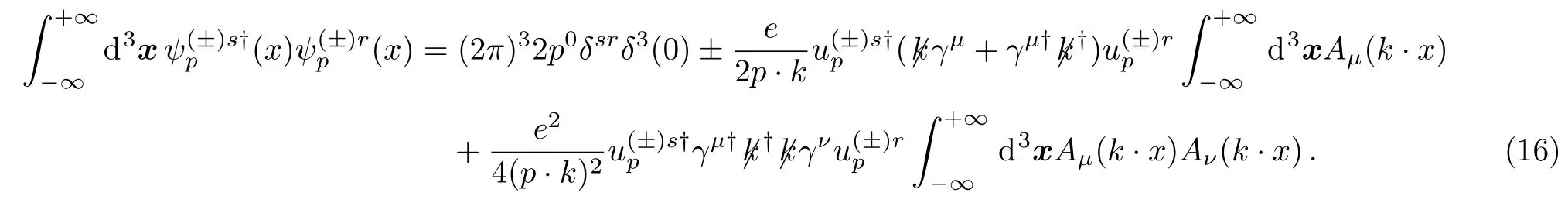
The three-dimensional space integration of the external electromagnetic vector potential yields
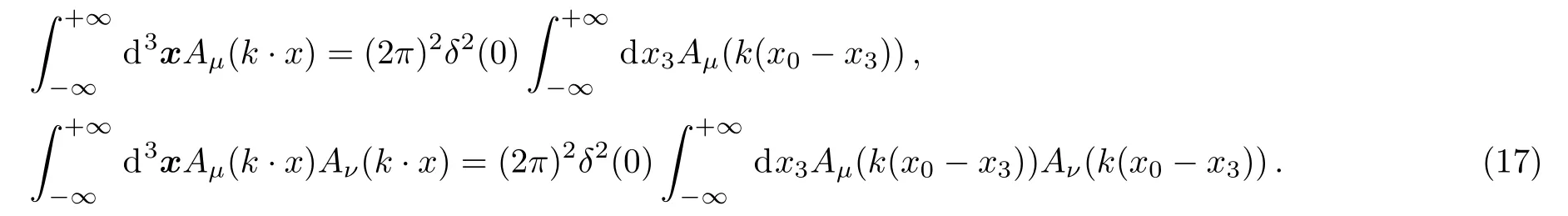
In the applications to venue of laser or collider where the electromagnetic vector potentialAμ(η)is bounded,thex3-integration at a fixed time in the equations is finite.The second and third terms on the right-hand side of Eq.(16)are infinitesimally small and ignored as compared to the first term.Then Eqs.(15) and (16) give
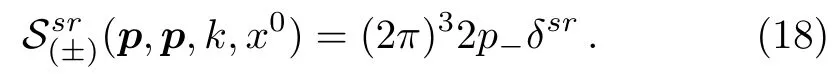
Substituting Eq.(18) to Eq.(15) and collecting up Eqs.(14) adn (15),we write the orthonormality of the Volkov solutions in a compacted expression
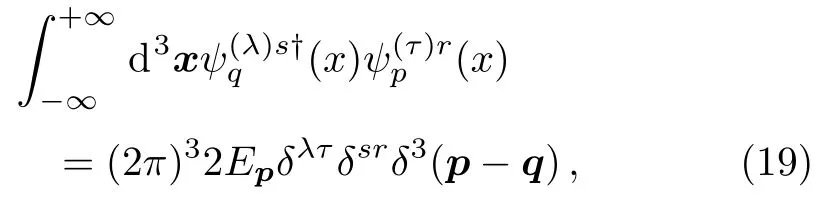
with the superscriptsλandτunderstood as the spin index+ or?.
In mathematics the boundedness of the potential is an over-constrained requirement to make the second and third terms of Eq.(16) vanished.Loosely speaking,the potential can allow various poles at certain values ofkandx0,but itsx3-integration should not be singularities as severe asδ(0),that is
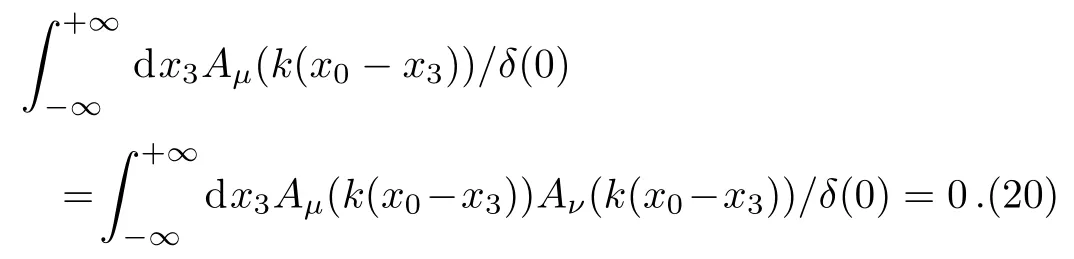
This is the least-constrained sufficient condition to the orthonormality of the Volkov solutions.
One subtlety has been hiden in the above derivation.The hermiticity definition of an operatoris (?,φ) =(,φ)for any two state vectors?andφ.To demonstrate the orthonormality of the Volkov solutions,we only need instead
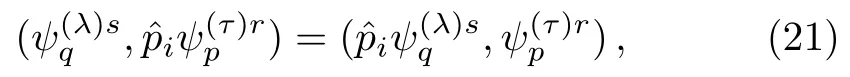
which implies
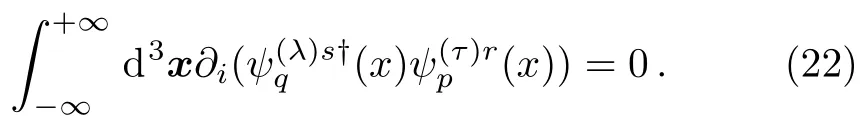
This equation should be satisfied automatically by the Volkov functions or be prescribed as boundary conditions of the functions at infinity,which corresponds to the orthonormality without or with boundary conditions to our purpose.Using Eqs.(9) and (10),one can find that the orthonormal Volkov functions happen to meet the equation
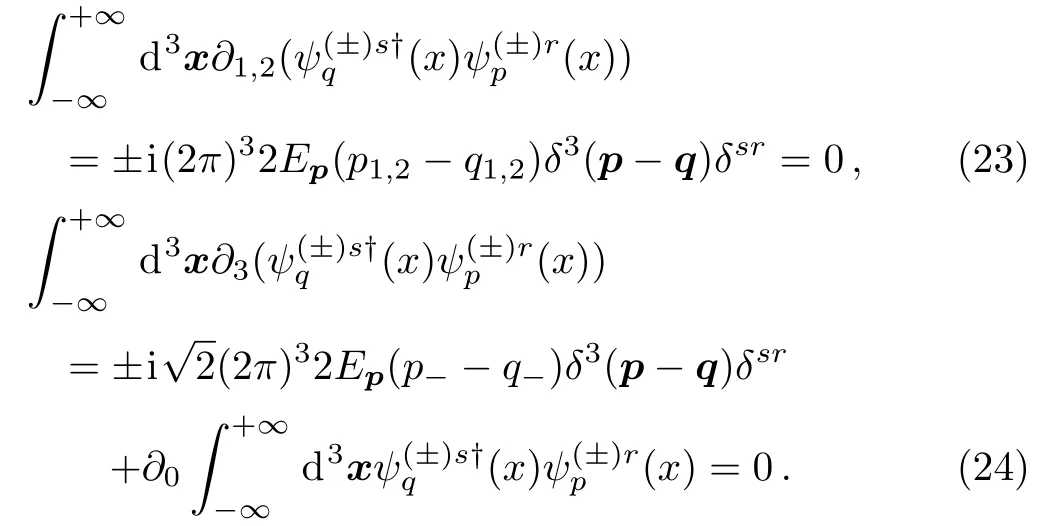
We have made a demonstration on the orthonormality of the Volkov solutions in the context of QM.As compared to the existed ones,[61?66]such a simple and physical demonstration can give us a clear thread on the condition under which the orthonormality is available.It is explicitly shown that the space-integration of external electromagnetic vector potential can not be singularities as severe as delta functions though the potential allows various poles at certain values of space and time.This is the least constrained condition and can be meet easily in applications.
What does the above demonstration mean when applying the Volkov solutions to IFQED? In quantum field theory,theare not mechanical operators anymore.The fermion field four-momentum operatorsPμare instead defined by
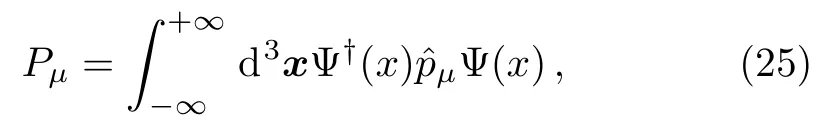

Prescribing the equal-time anti-commutation relations for the field and it’s canonical momentum Π(x)=iΨ?(x),a perturbative quantum field theory is built in the Furry space in which the four-momentumPμrequires to be hermitian.From Eq.(25),the differential operatormust be self-adjoint in the space expanded by the Volkov solutions.This validates the application of the above demonstration of the orthonormality to IFQED.
We have selected a special reference frame where the external plane wave propagates along the third-axis in the above discussion to obtain the orthonormality.SinceEpδ3(p ?q) is Lorentz invariant,Eq.(19) is independent on the reference frame selection.The sufficient condition thus need to be generalized to the expression that the space-integration of external electromagnetic vector potential can not be singularities as severe as delta functions though the potential allows various poles at certain values of space and time.
3 Representation Independent Calculation of the Inner Products
We have shown the orthonormality of the Volkov functions which are eigenfunctions of three independent hermitian operators and found a least-constrained sufficient condition to the orthonormality.We are going to make a direct calculation of the inner products of the functions in this section,following the work in the light-cone coordinate[61]and making use of Eq.(4) to avoid employing any explicit representation of the Dirac matrices and the spinors.If the sufficient condition is universal,it must manifest itself and can be tested in the calculation.Moreover,this presents a representation-independent and rigorous direct demonstration of the orthonormality,and facilitates the study of the polarized electron production where a convenient representation is usually selected.
The light-cone coordinate and the corresponding momentum we adopt are
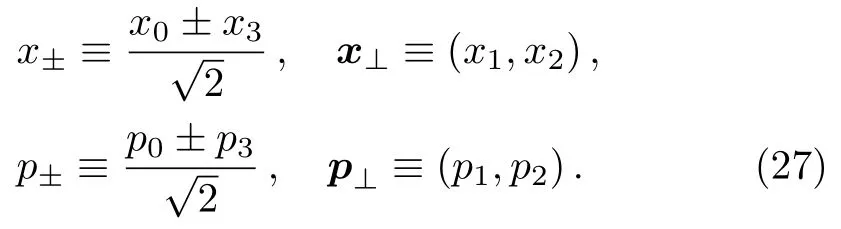
When observing in the reference frame where the external plane wave propagates along the third-axis,the Volkov functions can be written as
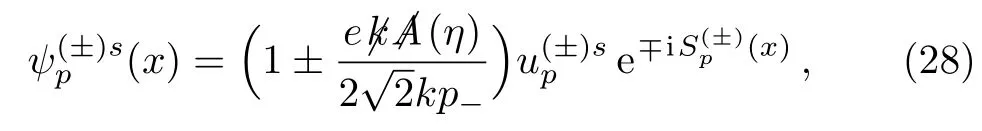
with the light-cone expressions of the parameters

and the phase

By exploiting the light cone expression (28),we start by calculating the inner products between the positive frequency functions and between the negative frequency ones
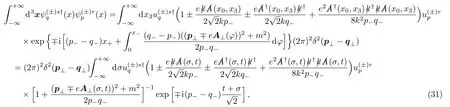
whereσis the transformed integral variable
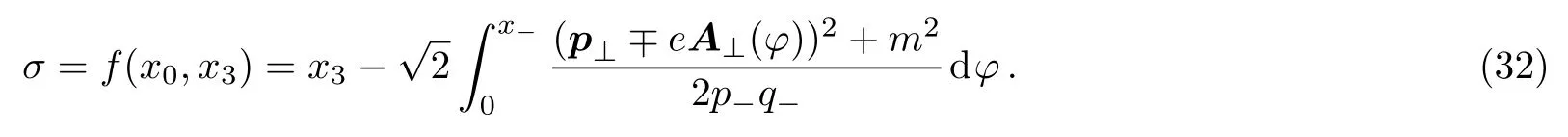
In the same way,we can calculate the inner product between the positive and negative functions
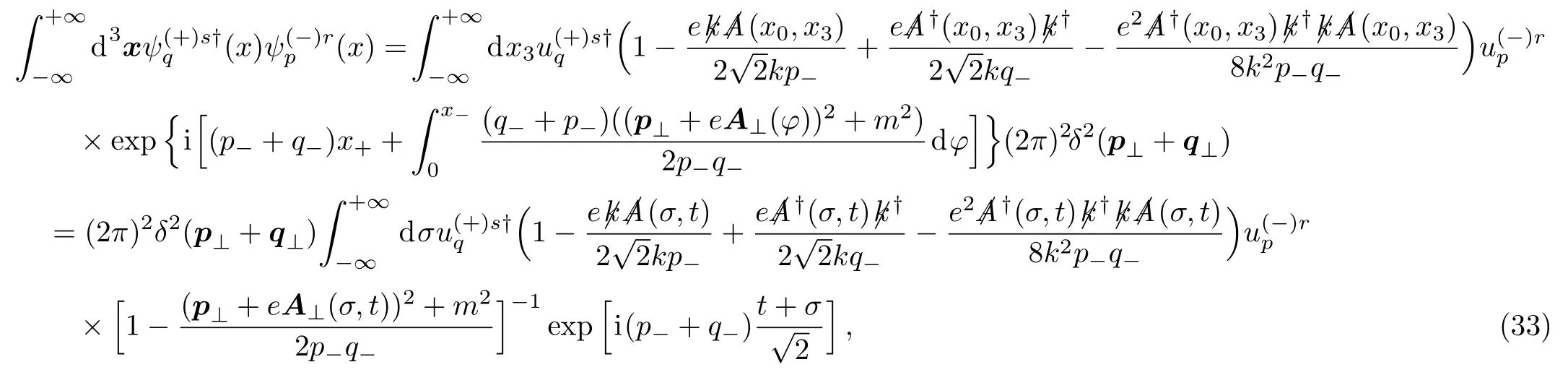
with the integral variable transformation
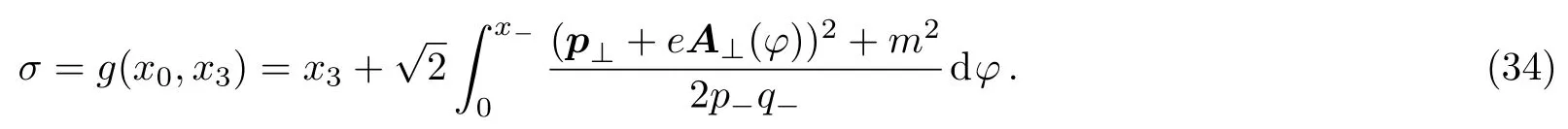
The integral variable transformations (32),(34) and the integration limits ofσdeserve an elaborate analysis.They are vital to the orthonormality and act as a test to the sufficient condition (20).In mathematics the integral variable transformations are valid when the firstσ-derivatives of the inverse functionsf?1(x0,σ)andg?1(x0,σ)are continuous at the intervalσ ∈(?∞,+∞) for a fixedx0.This requiresA⊥(x0,x3) to be continuous inx3.Meanwhile the integration limits ofσare the same as that ofx3∈(?∞,+∞) for a fixed time when Eq.(20) is satisfied,as can be seen straightforward from
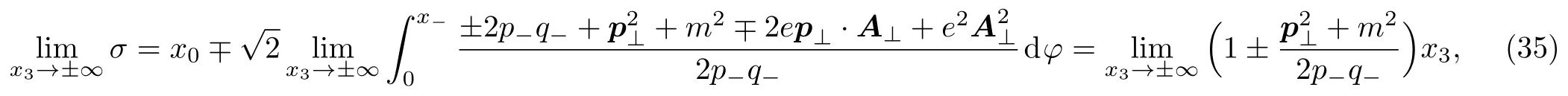
It is obvious that Eqs.(31) and (33) will be orthonormal if the following equations hold
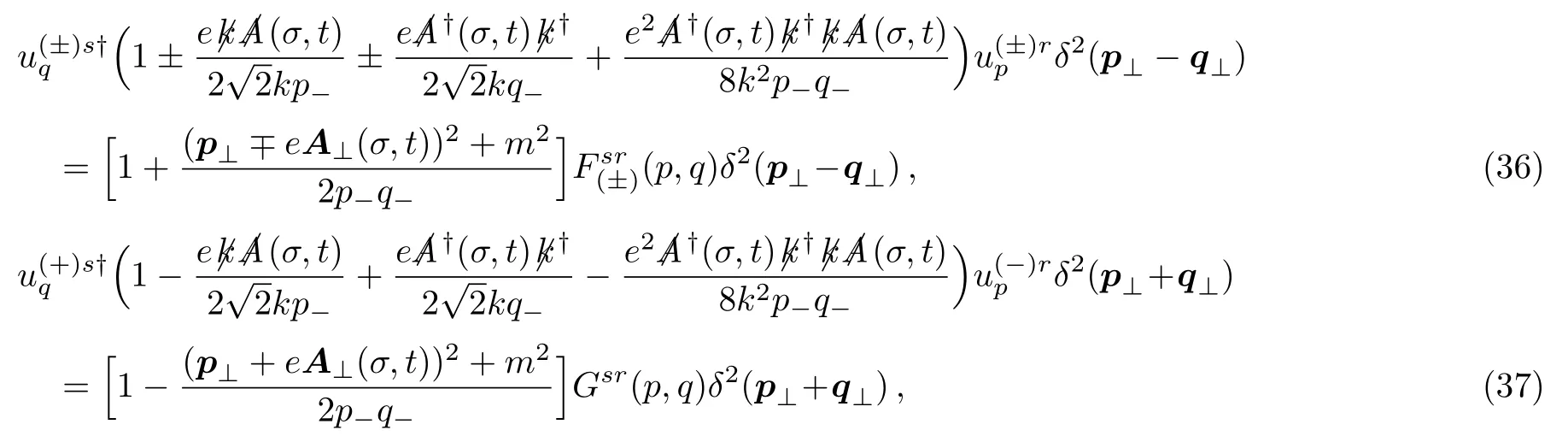
where theF(p,q) andG(p,q) are matrices represented by the spin freedom and the elements are ofσ-independence.In what follows we will try to find out that Eqs.(36) and (37) do hold,regardless of the explicit representation of the Dirac matrices and spinors.By means of idempotence law,each equation can be decomposed into three ones in terms of the powers ofAμ.The Eq.(36) then leads to
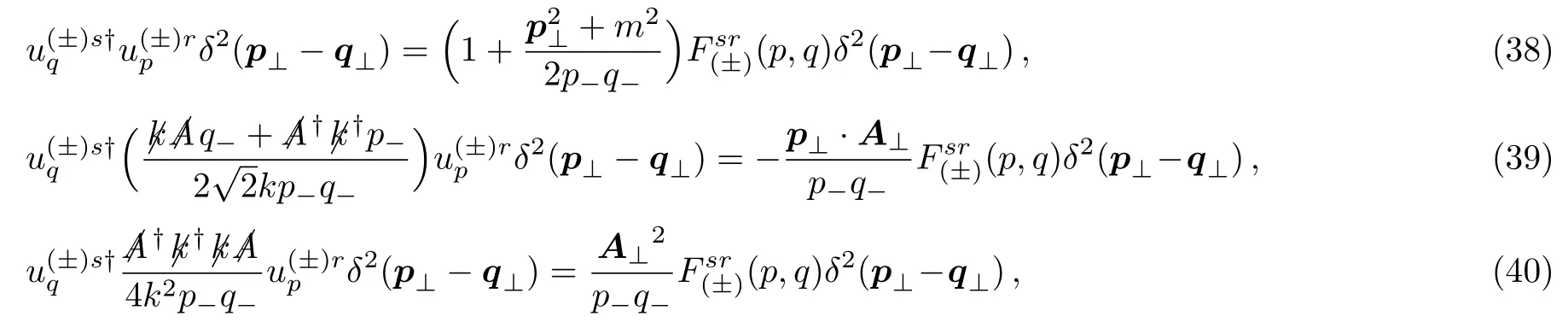
and Eq.(37) as well gives
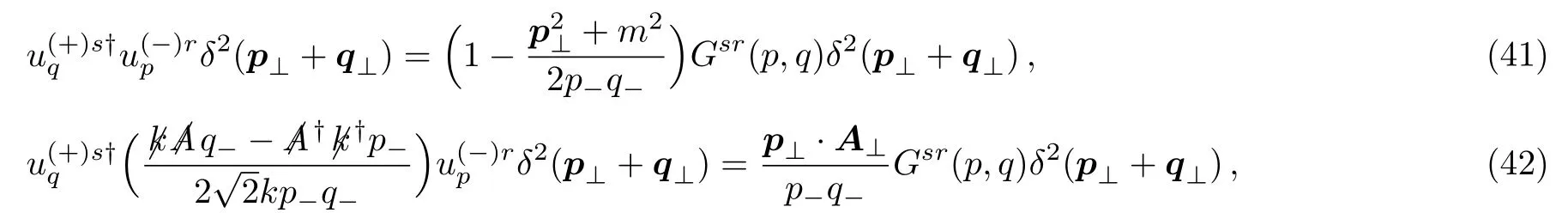

We can derive the normalizations atqμ=pμand=pμfrom Eqs.(5),(38),and (41)
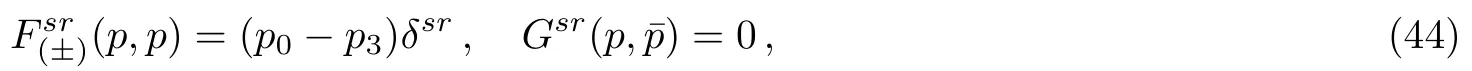
and the expressions forandGsr(p,q)δ2(p⊥+q⊥) from Eqs.(38) and (41).Substituting the expressions to Eqs.(39),(40),(42),and (43) and noticing Eq.(29),one can have
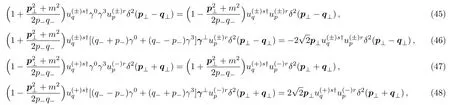
withγ⊥=(γ1,γ2).
We now exploit Eq.(4) to obtain identities
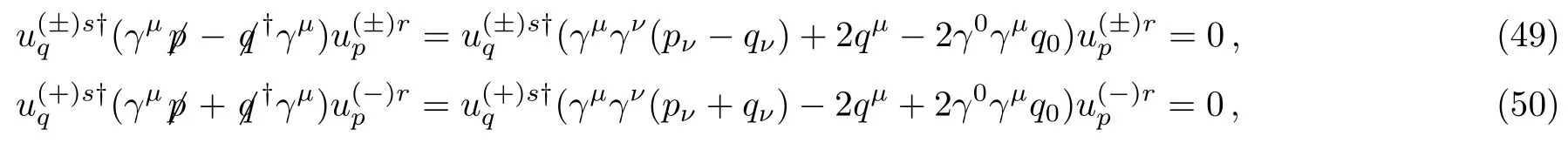
which are useful in further manipulating the Eqs.(45)–(48).Takingμ=0,1,2 respectively and performing the calculations atp⊥=q⊥in Eq.(49) andp⊥=?q⊥in Eq.(50),the identities yields
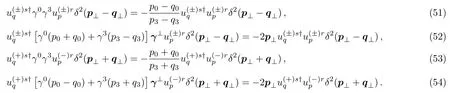
The spinor structures in Eqs.(45)–(48)are the same as those in Eqs.(51)–(54)respectively.By canceling the righthand side of Eqs.(45)–(48)with Eqs.(51)–(54)and expressing the resulting equations in a single spinor structures,we obtain three equations which amount to the verification of Eq.(36).
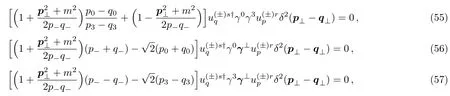
and the other three equations relating to Eq.(37),

If these equations are all satisfied,then Eqs.(36) and (37) hold and the orthonormality of the Volkov functions will be proven.Employing Eq.(27) and,it is easy to find that the momentum factors in the square brackets are all vanished.Thus we have verified the Eqs.(36) and (37) in a representation independent manner.
Substituting Eq.(36) to Eq.(31) and Eq.(37) to Eq.(33) respectively,we can then have the orthonormality for the Volkov functions

where we have employed
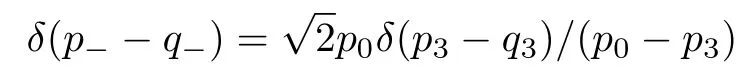
whenp⊥=q⊥,(p?+q?)>0 and the normalizations(44).
4 Summary
We have revisited the orthonormality of Volkov functions and derived a sufficient condition to the orthonormality.The sufficient condition requires that the spaceintegration of external electromagnetic vector potential can not be singularities as severe as delta functions though the potential allows various poles at certain values of space and time.It is a loose condition and can be meet easily in applications.
By aligning the external electromagnetic wave along the third-axis,the Volkov functions are eigenfunctions of the momentum operators,and the light-cone hamiltonian operator,whereis the Dirac hamiltonian,with real eigenvalues in the context of QM.Corresponding to physical observables,the operatorsandare hermitian,which results in a derivation of the orthonormality of the Volkov functions when thex3-integration of the external potential is not singularity as severe asδ(0).By analyzing the hermiticity of the fourmomentum operatorsPμof the fermion field theory,we find that the demonstration is valid in IFQED.We then made a direct calculation to the inner products of the solutions and proved the orthonormality in a general and rigorous manner without dependence on the explicit representation of the Dirac matrices and the spinors.In doing the calculation we can not only test the sufficient condition but also solidate the study of the polarized electron production in which a convenient representation to project out the spin-polarization is usually adopted.
——邢偉中檀香扇作品欣賞
 Communications in Theoretical Physics2019年10期
Communications in Theoretical Physics2019年10期
- Communications in Theoretical Physics的其它文章
- Mapping Between Charge-Dyon and Position-Dependent Mass Systems?
- Magnetic Properties of an Antiferromagnetic Spin-1/2 XYZ Model in the Presence of Different Magnetic Fields: Finite-Size Effects of Inhomogeneity Property?
- Superstatistics of Modified Rosen-Morse Potential with Dirac Delta and Uniform Distributions
- Modeling of Neurodegenerative Diseases Using Discrete Chaotic Systems
- Coupling Instability of a Warm Relativistic Electron Beam with Ion-Channel Guiding
- Design of Tunable Devices at Terahertz Frequencies Based on Quasi-Photonic Crystals Incorporated with Graphene
