First principles study of interactions of oxygen–carbon–vacancy in bcc Fe*

Yuan You(由園),Mu-Fu Yan(閆牧夫),Ji-Hong Yan(閆紀紅),Gang Sun(孫剛),and Chao Wang(王超)

1School of Materials Science and Engineering,Qiqihar University,Qiqihar 161006,China

2National Key Laboratory for Precision Hot Processing of Metals,School of Materials Science and Engineering,Harbin Institute of Technology,Harbin 150001,China

3School of Mechatronics Engineering,Harbin Institute of Technology,Harbin 150001,China

Keywords:interaction,first principles,oxygen,vacancy

1.Introduction

Carburizing[1–9]and nitriding[10–18]are common surface modification methods extensively used to enhance hardness and wear resistance of metallic materials.Furthermore,oxidization[19–26]has been used to improve the corrosion resistance of carburized or nitrided iron-based alloys in the last decades. In the process of carburizing,nitriding,or oxidizing,these small radius atoms(i.e.,C,N,or O)initially diffuse into Fe lattice and form an iron-based solid solution.The ironbased solid solution containing C,N,or O is known as a diffusion layer in carburized,nitrided,or oxidized surface layer.In a diffusion layer,the concentration of solutes gradually decreases from surface to core.When the concentration exceeds their solubility limit,the solutes tend to precipitate as carbides,nitrides,or oxides.[27]These precipitates,such as Fe3C,[28–32]Fe5C2,[28,31]Fe4N,[33–35]Fe2?3N,[33,34,36,37]Fe16X2(X=C or N),[38–40]Fe3O4,[41]Fe2O3,[42]Cr23C6,[43,44]Cr7C3,[32,43–45]Cr2N,[46]and CrN[47]have been extensively investigated.These compounds play a key role in determining the mechanical properties[27](hardness,wear resistance,etc.) of carburized, nitrided or oxidized layers. However, these studies are not enough to illuminate the atomistic diffusion mechanisms[48]of these small radius atoms(C,N,or O).

To explore the atomistic diffusion mechanisms of these small radius atoms(C,N,or O),one has to face an elementary and important issue,i.e.,the interactions of O with C.To study these interactions on an atomic scale,ab initio calculation based on the density functional theory is today the most powerful and appropriate method.Kamminga et al.[49]calculated the interactions of N with Ti,V,Cr,Ni,and Mo.Jiang and Carter[50,51]studied the dissolution and diffusion of C atom in ferrite and austenite,as well as the adsorption and diffusion of C atom into Fe(110)and Fe(100)surfaces from first principles calculations.The interactions of a C or an N atom in α-Fe with a vacancy,other C or N interstitial,as well as self–interstitial atoms have been discussed by Domain et al.[52]F?rst et al.[53]predicted the defect phase diagrams as a function of total carbon and vacancy concentration. Fu et al.[54]found that oxygen shows a high affinity for vacancies.Fors and Wahnstr?m[55]obtained that boron predominantly enters,as substitutional solute atoms,into α-iron.The calculations by Ye et al.[56]showed that the nitrogen vacancy acts as a deep donor in wurtzite AlN and a shallow donor in zinc-blende AlN.Sandberg et al.[57]investigated the dissolution and migration of C atom in bcc Fe as well as the formation enthalpies for carbides. A repulsive O–O interaction(0.4 eV)was obtained by Jiang et al.[58]Ohnuma et al.[59]studied the interactions between a vacancy and C/N atoms.Simonovic et al.[60]studied the interaction between C and Si in bcc Fe.Chen et al.[61]investigated the migrations of hydrogen(H)and helium(He)atoms in β-phase scandium(Sc),yttrium(Y),and erbium(Er)hydrides with three different ratios of H to metal.The diffusion coefficients of several alloying elements(Al,Mo,Co,Ta,Ru,W,Cr,Re)in Ni were calculated by Wu et al.[62](Y,Yi,O)clusters in FeCr matrix were simulated by Claisse et al.,[63]and obtained that the migration energy of O is 0.48 eV.The migration barriers and interactions of boron with point defects were characterized by Bialon et al.,[64]showing that substitutional boron binds strongly to interstitial point defect with dumbbell formation. In an investigation into the diffusivity of O in bcc Fe with and without the effect of vacancy,Shang et al.[65]found that the vacancy increases dramatically the migration energy barrier(from ～0.5 eV up to 0.0 eV)for O diffusion in bcc Fe.Interactions between vacancies and interstitial solutes(C,N,and O)were studied by Barouh et al.,[27]and showed that the solubility limit of O in Fe is largely affected by the presence of smallclusters.The lowest energy migrations of small(X=C,N,and O)clusters were investigated by Barouh et al.,[66]indicating that the dominant clustersandhave very reduced mobility compared with isolated solutes. Wang et al.[67]investigated the carbon segregation in bcc iron symmetrical tilt grain boundaries and reported that the attraction of C atoms to GBs is in general stronger than to dislocations and vacancies.Souissi et al.[68]performed systematic calculations to show that the migration energy values of C,N,B,and O are 0.87 eV,0.72 eV,0.67 eV,and 0.50 eV,respectively.A database of solute–solute interactions in bcc Fe was developed by Gorbatov et al.[69]Li et al.[70]studied the diffusion mechanism of boron in bcc–Fe and predicted that the dominant diffusion mechanism in bcc–Fe is the interstitial mechanism through an octahedral interstitial site.Wang et al.[71]reported that the vacancy formation energy decreases with the distance between vacancy and grain boundary(GB)plane decreasing.Versteylen et al.[72]carried out a number of calculations to investigate the diffusivities of substitutional impurity elements in iron.Ross et al.[73]investigated the curved pathway of O in Al and obtained that O prefers to sit on the tetrahedral interstitial site just opposite to the octahedral site.Lüthi et al.[74]investigated the attractive interaction between interstitial solutes(B,C,N,O)and screw dislocations in bcc iron.Zhang et al.[75]characterized oxygen behaviors in vanadium and obtained that O prefers octahedral interstitial sits in V,and a strong repulsive interaction exists in the nearest neighbors O–O pair.Akshaya et al.[76]studied the interaction energy of atomic defects in bcc iron,their relevant results are compared with our investigations.Ouyang et al.[77]reported that the segregated U vacancy on U/Al interface can act as a sink for H and O impurities.Studied in our previous work were the interactions of La–C/N,[78]La–FSA(here FSA stands for foreign substitutional atom,i.e.,Al,Si,Ti,V,Cr,Mn,Co,Ni,Cu,Nb or Mo),[79]C/N–FSA,[80]C–N,and C–N–vacancy[81]in bcc Fe.However,the interactions of O with C in bcc Fe without and with a vacancy have not been studied.

In this paper,first principles calculations are carried out to study the interactions of oxygen–carbon–vacancy(here vacancy is denoted as symbolin bcc Fe. By constructing possible configurations of a single O atom,in bcc Fe,the preferred occupation of oxygen and the interactions ofandare investigated.Density of states,electron density difference,and Mulliken bond population are also analyzed.The comparisons are made between our results and data obtained by others.

Quantitative descriptions about the behaviors of O and the interactions of C–O andare obtained in this work,it will be beneficial to understanding the atomistic diffusion mechanism of O in iron-based alloy with C and vacancy.Furthermore,all the configurations in this work can be used to construct C–O potential,and this potential can be used to simulate the diffusion behaviors of O in bcc Fe on a greater scale.

2.Computational methods

Our first principles calculations are based on density functional theory (DFT) and carried out with CASTEP code.[82]The ion–electron interaction is modeled by ultrasoft pseudopotentials of the Vanderbilt type.[83]Exchange–correlation functions are described in the spin-polarized Perdew–Burke–Ernzerhof generalized gradient approximation(GGA-PBE).[84]For C,O,and Fe,the numbers of valence electrons are 4,6,and 8,respectively,(reference 2s22p2for C,2s22p3for N,and 3d64s2for Fe).The cutoff energy on the wave function is taken to be 350 eV and the convergence criterion for electronic self-consistency is 5×10?7eV per atom.The wave functions were sampled on a 3×3×3k-point mesh constructed by using the Monkhorst and Pack scheme.[85]

In our calculations,these supercells are composed of 3×3×3 bcc unit cells with 54 Fe atoms.The ion relaxations are performed by using the Broyden–Fletcher–Goldfarb–Shanno(BFGS)method[86]implemented in the CASTEP code.These relaxations are done in a constant volume,thus only the atomic coordinates are optimized in a supercell dimensioned with the equilibrium lattice parameter of bcc Fe.

For a supercell containing m Fe atoms and a foreign atom(FA),the solvation energy(Es)can be calculated from

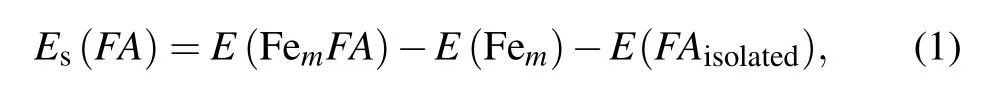
where E(FemFA)is the energy of the supercell containing m Fe atoms and an FA,E(Fem)is the reference energy of bulk Fe with the same structure(bcc)as in FemFA,and E(FAisolated)is the energy of an isolated FA(a single FA alone in a supercell).The foreign atom can be C or O.With the scheme,the more negative the FA solvation energy,the more stable the configuration FemFA will be.

The interactive energy(Ei)of n interacting entities(defects and impurities),(A1,...,An),is calculated from

where E(Ai)is the energy of the supercell containing an entity Aionly,E(A1+···+An)is the energy of the supercell containing all entities(A1+···+An),and Erefis the energy of a perfect supercell.According to the equation,the positive interactive energy means repulsion among these entities,while negative interactive energy indicates attraction.

3.Results and discussion

Our calculations are divided into three parts.Firstly,the occupation and migration behaviors of an oxygen atom in bcc Fe are investigated.Secondly,both C and O are incorporated into bcc Fe cell and occupy the most stable positions obtained in the first part,and the interactions between C and O are calculated.Thirdly,a vacancy is introduced into bcc Fe cell,and the interactions of a vacancy with C and O atoms are studied.

3.1.Oxygen atom in bcc Fe

When an oxygen atom is incorporated into a bcc Fe cell,it possibly occupies a substitutional(Sub),octahedral(Oct)interstitial or tetrahedral(Tet)interstitial site as shown in Fig.1.

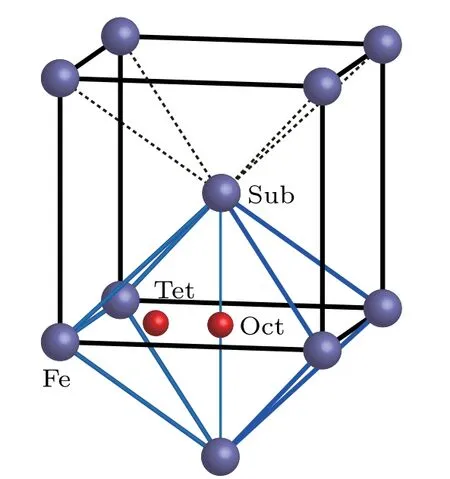
Fig.1.Possible sites of an oxygen atom in bcc Fe.

Solvation and migration energy values of an O(or C)atom in bcc Fe are listed in Table 1. Solvation energy values of a C atom at different positions in bcc Fe are ?4.75 eV,?7.15 eV,and ?6.20 eV,respectively.Solvation energy values of an O atom at different positions in bcc Fe are ?1.31 eV,?2.89 eV,and ?2.43 eV,respectively.The solvation energy values of C are all more negative than those of O at the same position in bcc Fe.A C atom in bcc Fe is more stable than an O atom in bcc Fe at our considered three positions.All solvation energy values of an O atom at different positions in bcc Fe are negative.An O atom can stay stably in bcc Fe at different positions.The most negative solvation energy(?2.89 eV)is obtained for an O atom at an octahedral interstitial site in bcc Fe.Therefore,the octahedral interstitial site is the most stable position for an O atom in bcc Fe,which is the same as the scenario of a C atom in bcc Fe.

Furthermore,small energy differences(≤0.10 eV)are obtained in this work from 3×3×3(before a comma)to 4×4×4(after a comma)bcc Fe supercell as shown in Table 1.Therefore,a 3×3×3 supercell is sufficient to ensure the accuracy of our following calculations.

Table 1. Solvation energy(Es)and migration energy(in unit eV)of an FIA(C or N)in 3×3×3(before a comma)and 4×4×4(after a comma)bcc Fe supercell.In configurationsand,FIA occupies separately Sub,Oct,and Tet sites in bcc Fe as shown in Fig.1.Migration energyof FIA in bcc Fe is difference between energy values of two configurations andOur migration energy values of O and C are compared with those in Refs.[50],[52],[55],[64],[65],and[68].

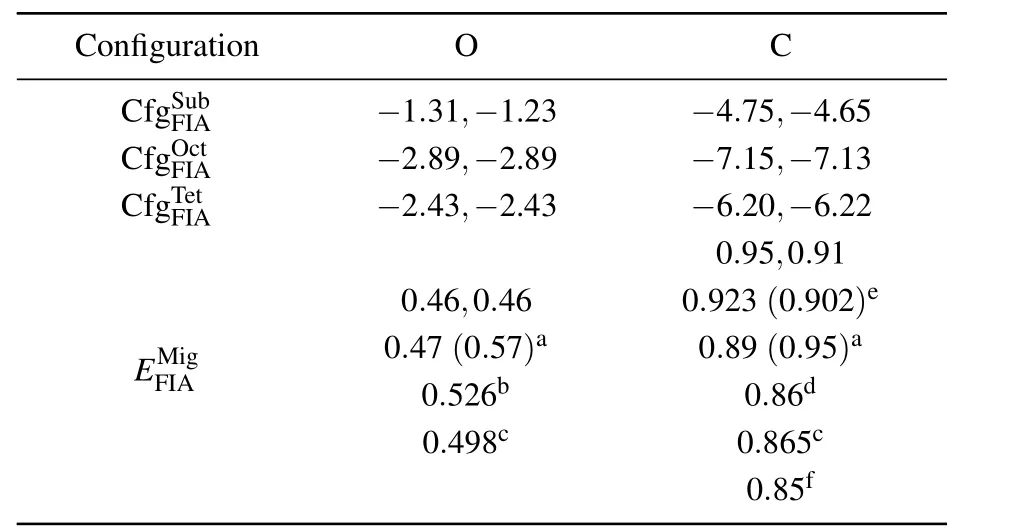
Table 1. Solvation energy(Es)and migration energy(in unit eV)of an FIA(C or N)in 3×3×3(before a comma)and 4×4×4(after a comma)bcc Fe supercell.In configurationsand,FIA occupies separately Sub,Oct,and Tet sites in bcc Fe as shown in Fig.1.Migration energyof FIA in bcc Fe is difference between energy values of two configurations andOur migration energy values of O and C are compared with those in Refs.[50],[52],[55],[64],[65],and[68].

a[64],b[65],c[68],d[50],e[52],f[55].

Configuration O C CfgSFuIAb ?1.31,?1.23 ?4.75,?4.65 CfgOFIcAt ?2.89,?2.89 ?7.15,?7.13 CfgTFeIAt ?2.43,?2.43 ?6.20,?6.22 0.95,0.91 0.46,0.460.923(0.902)e EFMI A ig0.4 0 7.5(0 2.65b7)a0.89 0.(806.d9 5)a 0.498c0.865c 0.85f

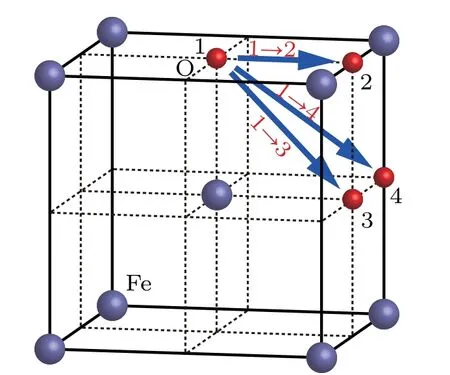
Fig.2.Possible migration paths of an O atom in bcc Fe.

Migration energy of an O atom in bcc Fe can be obtained by the method of transition state search(TSS).The possible migration paths of an O atom in bcc Fe are shown in Fig.2,in which the O atoms marked as 1,2,3,and 4 stay at different octahedral interstitial sites in the bcc Fe.In path 1 →2,the O atom moves from position[0,0,0]to[1/2,0,0].In path 1 →3,the O atom moves from position[0,0,0]to[1/2,1/2,0].In path 1 →4,the O atom moves from position[0,0,0]to[1/2,1/2,1/2].In the bcc Fe,the migration energy values of an O atom are 0.46 eV and 1.82 eV along path 1 →2 and 1 →4 direction,respectively.As shown in Fig.3,along path 1 →2,the minimum migration energy is obtained to be 0.6 eV,which is equal to the difference between energy valyes at tetrahedral site and octahedral interstitial site.Therefore,path 1 →2 is the most possible migration path of an O atom in the bcc Fe.In path 1 →2,the two sites marked as 1 and 2 are the first nearest neighbors to each other in octahedral sites in the bcc Fe.From the site marked as 1 to the site marked as 2,a tetrahedral site is just in the middle of the path.Therefore,the most possible migration path of an O atom in bcc Fe is from one octahedral interstitial site to its first nearest neighbor octahedral interstitial site,in which a tetrahedral site is just in the middle of the two sites.

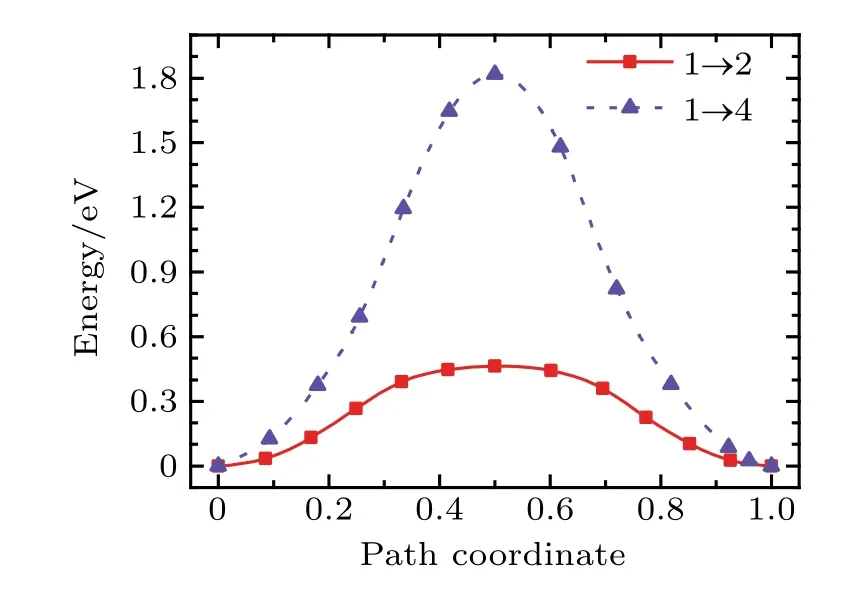
Fig.3.Variations of migration energy with path coordination of an O atom in bcc Fe along different directions.

According to the migration energy(0.46 eV)of an O atom in bcc Fe,obtained by TSS,the migration energy of a C or O atom in bcc Fe is approximately equal to the difference between the energy values at tetrahedral and octahedral interstitial sites as shown in Table 1.The migration energy of a C or an O atom in bcc Fe is 0.95 eV or 0.46 eV,respectively.Our migration energy values of O and C are in agreement with previous results in Refs.[50],[52],[55],[64],[65],and[68].The migration energy of an O atom is smaller than that of C and equal approximately to the half of that.

In Fig.3,the migration energy of the path 1 →3 is absent,because the path 1 →3 is not used and the O atom moves along the path 1 →2 →3.It is also indirect evidence that the path 1 →2 is the most possible migration path of an O atom in bcc Fe.

In the bcc Fe,the maximum migration energy(1.82 eV)of an O atom is obtained along the path 1 →4. This is because the middle point of the path 1 →4 is just located in the close-packed direction[1 1 1]of bcc Fe.

Figure 4 shows the bonds around an octahedral interstitial site without FIA or with FIA in the bcc Fe.Summarized in Table 2 are the number,length(in unit ?A)and population of the bonds around an octahedral interstitial site in each of bulk Fe,andAs shown in Fig.4(a)and Table 2,there are 8 Fe–Fe(1nn that refers to the first nearest neighbor),5 Fe–Fe(2nn that refers to the second nearest neighbor)and 2 Fe–Fe(3nn that refers to the third nearest neighbor)bonds around an octahedral interstitial site in bcc Fe.In the Fe–Fe(1nn)bond,two Fe atoms are the first nearest neighbors to each other and aligned along the?111?direction. The population of Fe–Fe(1nn)bond is 0.26,which can be defined as Fe metallic bond.In Fe–Fe(2nn)and Fe–Fe(3nn)bonds,two Fe atoms are the first and second nearest neighbor to each other and aligned along the?100?and?110?direction,respectively.Population of Fe–Fe(2nn)and Fe–Fe(3nn)bonds are 0.08 and ?0.18,respectively.The sum of bond populations around an octahedral interstitial site in bcc Fe is 2.12.

Fig.4.Bonds around an octahedral interstitial site(a)without or(b)with FIA in bcc Fe.

Table 2.Number,length(in unit ,and population of the bonds around an octahedral interstitial site in each of bulk Fe,,and Last column shows sum of bond populations around octahedral interstitial site.

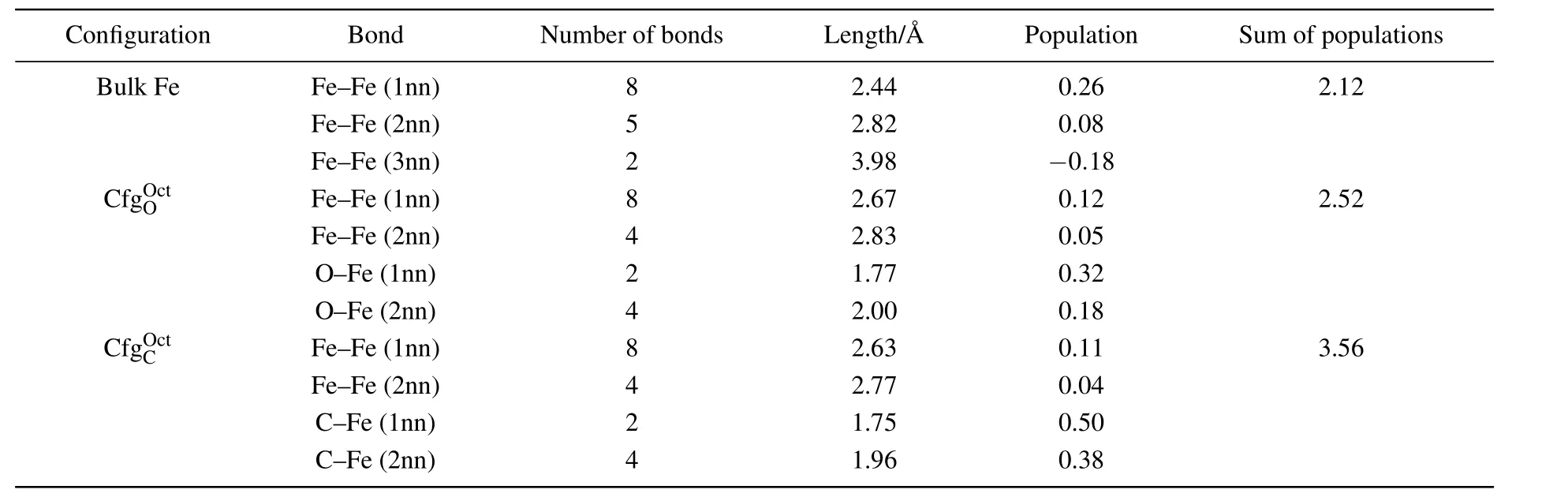
Table 2.Number,length(in unit ,and population of the bonds around an octahedral interstitial site in each of bulk Fe,,and Last column shows sum of bond populations around octahedral interstitial site.

Configuration Bond Number of bonds Length/A? Population Sum of populations Bulk Fe Fe–Fe(1nn) 8 2.44 0.26 2.12 Fe–Fe(2nn) 5 2.82 0.08 Fe–Fe(3nn) 2 3.98 ?0.18 CfgOOc t Fe–Fe(1nn) 8 2.67 0.12 2.52 Fe–Fe(2nn) 4 2.83 0.05 O–Fe(1nn) 2 1.77 0.32 O–Fe(2nn) 4 2.00 0.18 CfgOC ct Fe–Fe(1nn) 8 2.63 0.11 3.56 Fe–Fe(2nn) 4 2.77 0.04 C–Fe(1nn) 2 1.75 0.50 C–Fe(2nn) 4 1.96 0.38

As shown in Fig.4(b)and Table 2,there are 8 Fe–Fe(1nn),4 Fe–Fe(2nn),2 FIA–Fe(1nn),and 4 Fe–Fe(2nn)bonds around FIA in configurationPopulation of Fe–Fe(1nn)bond decreases from 0.26 to 0.11 for C and from 0.26 to 0.12 for O inThe population of Fe–Fe(2nn)bond also decreases from 0.08 to 0.04 for C and from 0.08 to 0.05 for O inThe 2 FIA–Fe(1nn)and 4 FIA–Fe(2nn)bonds form after an FIA has been incorporated into an octahedral interstitial site in bcc Fe.Bond population of C–Fe(1nn)and C–Fe(2nn)are 0.50 and 0.38,respectively.Bond population of O–Fe(1nn)and O–Fe(2nn)are 0.32 and 0.18,respectively.The strength of FIA–Fe(1nn)bond(0.50 for C and 0.32 for O)is greater than that of the Fe metallic bond(0.26).Sum of bond populations around FIA in configurationis 3.56 for C and 2.52 for O,separately.After an FIA is incorporated into an octahedral interstitial site in bcc Fe,the sum of bond populations around the octahedral interstitial site increases from 2.12 to 3.56(for C)and 2.52(for O),separately.Consequently,the strength of the material is enhanced after a small number of C or O atoms have been incorporated into iron-based alloy and a dilute solid solution has formed.And the strengthening effect of C is more significant than that of O.

As listed in Table 2,the lengths of C–Fe bonds are 1.75for 1nn and 1.96for 2nn,respectively.The lengths of O–Fe bonds are 1.77for 1nn and 2.00for 2nn,respectively.The length of O–Fe bond is greater than that of C–Fe bond in

3.2.Interactions of O with C

When two FIAs(two O atoms,two C atoms,or an O atom and a C atom)are incorporated into a bcc Fe cell,they can form seven possible configurations as shown in Fig.5. The interaction energy,relaxation,and bond population for each of C–C,O–O,and C–O in bcc Fe with different configurations are listed in Table 3.When one FIA is placed at the site marked as FIA1 and is assumed to be the origin of coordinate,another FIA denoted as 1 occupies the position of[1/2,0,0]in the configuration.The distance between two FIAs is(1/2)a0in.In,the FIA2 stays at the position of[1/2,1/2,0],and the distance between two FIAs isInthe FIA2 stays at the position of[1/2,1/2,1/2],and the distance between two FIAs isIn the configurationthe FIA2 stays at the position of[1,0,0]and the distance between two FIAs is a0.In the configurationthe FIA2 stays at the position of[1,1/2,0],and the distance between two FIAs isIn the configurationthe FIA2 stays at the position of[1,1/2,1/2],and the distance between two FIAs isIn the configurationthe FIA2 stays at the position of[1,1,0]and the distance between two FIAs isIn a bcc unit cell,there are 18 octahedral sites,which include 12 middle points of edges and 6 center points of faces.In the configurations as shown in Fig.5,the sites marked as 1,2,...,7 are representative octahedral sites.The sites denoted as 1,2,...,7 have 2,4,2,2,2,4,1 equivalent sites,respectively.

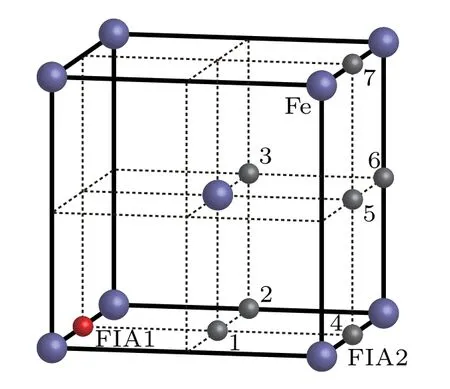
Fig.5.Possible configurations of O atom and C atom in a bcc Fe.

Table 3.Interaction energy(Ei),relaxation(in percent of ?d/d0),and bond population for each of C–C,O–O,and C–O in bcc Fe with different configurations.In(i=1,2,...,7),FIA2 can occupy octahedral interstitial site marked as i.d0:distance between two FIAs before relaxations,?d:change of distance between two FIAs after relaxations,a0:lattice parameter.For O–O and C–C,our interaction energy values are compared with those obtained by Akshay et al.,[76]given after the first comma.For C–C,our interaction energy values are compared with those obtained by Domain et al.,[52]given after the second comma.

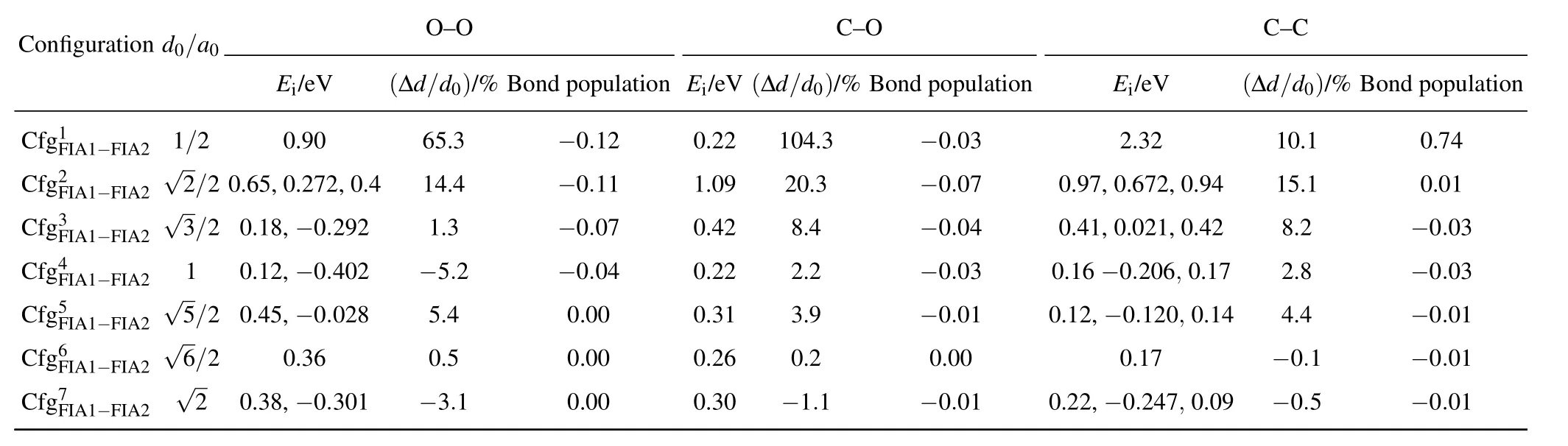
Table 3.Interaction energy(Ei),relaxation(in percent of ?d/d0),and bond population for each of C–C,O–O,and C–O in bcc Fe with different configurations.In(i=1,2,...,7),FIA2 can occupy octahedral interstitial site marked as i.d0:distance between two FIAs before relaxations,?d:change of distance between two FIAs after relaxations,a0:lattice parameter.For O–O and C–C,our interaction energy values are compared with those obtained by Akshay et al.,[76]given after the first comma.For C–C,our interaction energy values are compared with those obtained by Domain et al.,[52]given after the second comma.

Configuration d0/a0 O–O C–O C–C Ei/eV (?d/d0)/%Bond population Ei/eV(?d/d0)/%Bond population Ei/eV (?d/d0)/%Bond population CCC fff ggg 1F2F3F III AAA 111???FFF III AAA 222 √ √123///222 0 .06.1 58,,00?..92 070 2.2,9 0 2.4 611 54...3 34 ???000...110 217 010...204 292 120804..4.33 ???000...000 374 00..94 71,,00 2...60 372 221 ,,00 ..94 42 118 05...2 11 ?000..70.0 413 CCCC ffff gggg 4F5F6F7F IIII AAAA 1111????FFFF IIII AAAA 2222 √√√56 1//2 22 000...143 258,,,0? ? ?.3 0060.. .403 020 281 ??50 5 3..45..2 1 ?000 0...000.0 000 4 0000....2323 2160 ?2301...292.1 ? ? ?0 000.0...0000 311 00 0...12 122 6,, ? ? ?0000....1 2127 024 6 07,,,0 00...110 749 ? ?2400..84..15 ????0000....0000 3111

The interaction energy values for C–C,O–O,and C–O are all positive,indicating the repulsive interaction of C–C,O–O,and C–O in bcc Fe with different reconfigurations.The repulsion is the greatest in C–O,the smallest in O–O,and the middle for C–C,separately.With the increase of the distance for C–C,O–O,and C–O,in the configurations from 1 to 4,the interaction energy values decrease,and the repulsion becomes smaller and smaller.In the configurations from 5 to 7,the changes in the interaction energy are not obvious.

The interaction energy of C–O inis small(0.22 eV)and equal to that inIn the configurationas shown in Fig.5,C and O atoms sit at the sites marked as FIA1 and 1,respectively.After relaxation,the O atom moves from the site marked as 1 to the site denoted as 4.Then the configurationtransforms into the configurationThe motion from the site denoted as 1 to the farther site marked as 4 is due to the C–O repulsion.This is the direct evidence for the C–O repulsion.

As the FIA1–FIA2 distance is less than a0before relaxation,the FIA1–FIA2 distance becomes greater after relaxation. In the configurationsandthe O–O relaxations(?d/d0)are 65.3%and 14.4%,respectively.In the configurationsandthe C–O relaxations(?d/d0)are 104.3%,20.3%,and 8.4%,respectively.In the configurations,and,the C–C relaxations(?d/d0)are 10.1%,15.1%,and 8.2%,respectively.

The population of C–C bond inis 0.74,which means a covalent C–C bond forms.Except for C–C bond inall other C–C,C–O,and O–O bond populations are approximate to zero. In other words,except for C–C in the configuration,the interaction between two FIAs(C–C,C–O,and O–O)in(i=1,2,...,7)is approximate to zero after relaxations.

Figure 6 depicts the densities of states(DOSs)for Fe and O atoms in the configurationsand.For pure Fe atom as shown in Fig.6(a),the highest peaks(1.98 e/eV for α state and ?1.76 e/eV for β state)are situated at ?0.88 eV and 1.85 eV,respectively.

For the DOS of the O atoms in the configurationthere are two peaks as shown in Fig.6(b).In the density of α states for the O atom in the configurationthe first and second highest peaks(3.49 e/eV and 1.75 e/eV)are situated at ?9.09 eV and ?22.42 eV,respectively. In the density of β states for the O atom in the configurationthe first and second highest peaks (?3.39 e/eV and ?1.77 e/eV)are situated at ?8.75 eV and ?22.31 eV,respectively.

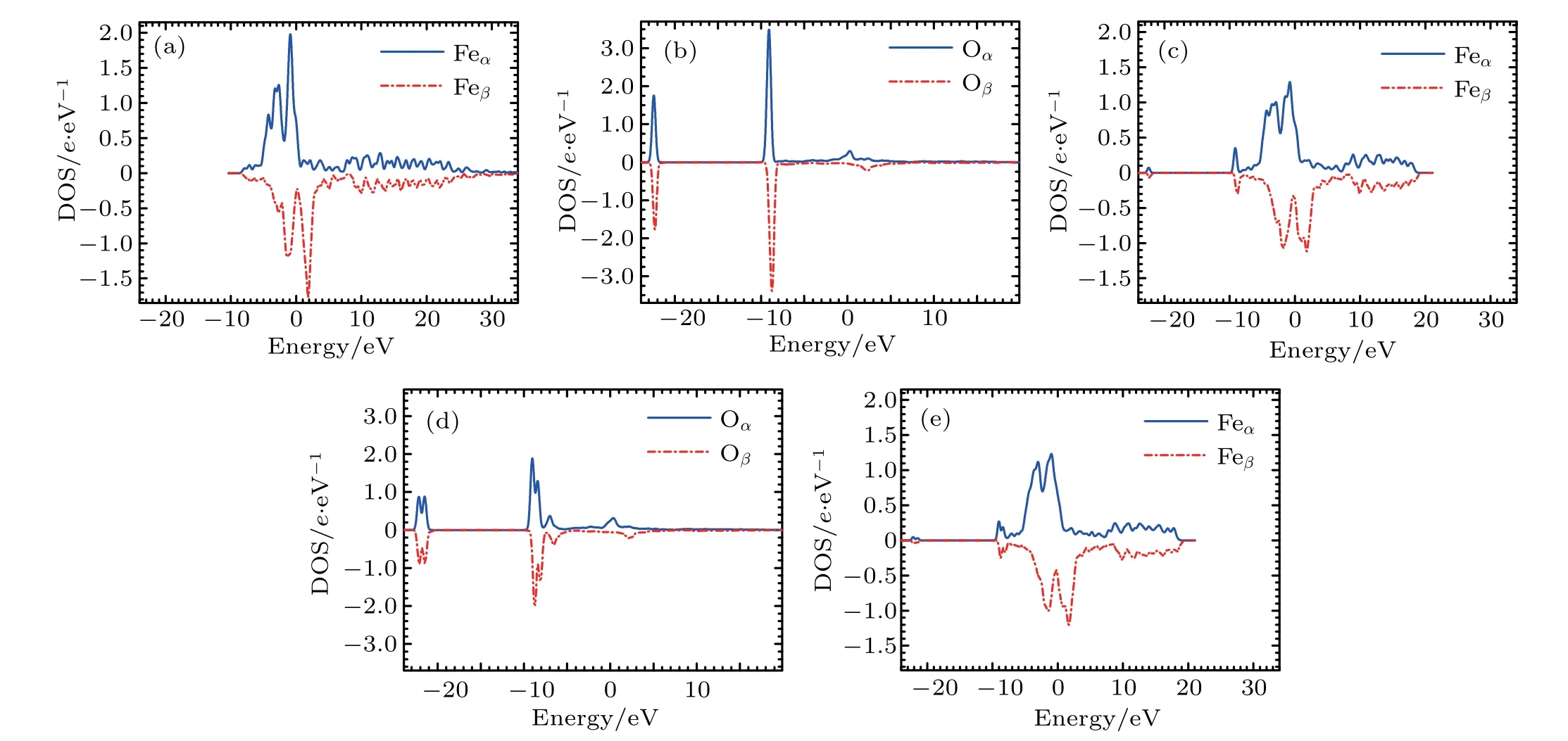
Fig.6.(a)DOS of Fe atoms in pure Fe,(b)DOS of O atoms in configuration(c)DOS of Fe atoms in the first nearest neighboring to O in configurationDOS of O atoms in configuration ,and(e)DOS of Fe atoms in the first nearest neighboring to O in configuration

The DOS of the Fe atoms in the first nearest neighboring to the O atom in configurationis shown in Fig.6(c).Compared with the DOS of Fe atoms in bcc Fe without O atom,the DOS of the Fe atoms in the first nearest neighboring O in configuration(see Fig.1)has the changes as follows.(i)There is an obvious depletion for the highest peak.The highest peaks(1.29 e/eV for α state and ?1.12 e/eV for β state)are situated at ?0.78 eV and 1.82 eV,respectively.(ii)There are two hybridizations.For the density of α states,the first and second highest peaks(0.35 e/eV and 0.07 e/eV)are situated at ?9.14 eV and ?22.42 eV,respectively.For the density of β states,the first and second highest peaks(?0.30 e/eV and ?0.07 e/eV)are situated at ?8.81 eV and ?22.31 eV,respectively.

In the DOS of the O atom inas shown in Fig.6(d),each peak is split into two parts.At higher energy level of α DOS,the first and second highest peaks(1.88 e/eV and 1.29 e/eV)are situated at ?9.03 eV and ?8.41 eV,respectively.At a higher energy level of β DOS,the first and second highest peaks(?2.04 e/eV and ?1.38 e/eV)are situated at?8.75 eV and ?8.09 eV,respectively.At a lower energy level of α DOS,the first and second highest peaks(0.88 e/eV and 0.87 e/eV)are situated at ?21.50 eV and ?22.16 eV,respectively.At a lower energy level of β DOS,the first and second highest peaks(?0.89 e/eV and ?0.88 e/eV)are situated at?21.46 eV and ?22.10 eV,respectively.

In the DOS of the Fe atom in the first nearest neighboring to O atom in configurationas shown in Fig.6(e),each hybridization peak is split into two.At the higher energy level of α DOS,the first and second highest peaks(0.27 e/eV and 0.19 e/eV)are situated at ?9.03 eV and ?8.40 eV,respectively.At a higher energy level of β DOS,the first and second highest peaks(?0.25 e/eV and ?0.17 e/eV)are situated at?8.75 eV and ?8.08 eV,respectively.At a lower energy level of α DOS,the first and second highest peaks(0.05 e/eV and 0.03 e/eV)are situated at ?22.16 eV and ?21.50 eV,respectively.At a lower energy level of β DOS,the first and second highest peaks(?0.04 e/eV and ?0.03 e/eV)are situated at?22.10 eV and ?21.46 eV,respectively.

In Table 4 summarized are the electronic distributions in different orbits,the values of charge(e)and magnetic moment(μB)of O atom and its neighboring Fe atom in configurationsand.In bulk Fe,the total electron number of Fe atoms is 8.00.The electron number in s,p,and d orbits of Fe atom are 0.68,0.69,and 6.62,respectively.The charge and magnetic moment of the Fe atom are 0.00 e and 2.20μB.For an isolated O atom,its total electron number is 6.00.The electron number in s and p orbits of an isolated O atom are 2.00 and 4.00,respectively.

Table 4. Electronic distributions in different orbits,values of charge(e),and magnetic moment(μB)of O atom and its neighbor Fe atom in configurations and

Table 4. Electronic distributions in different orbits,values of charge(e),and magnetic moment(μB)of O atom and its neighbor Fe atom in configurations and

Subshell Bulk Fe Fe in CfgOOc t O in CfgOOc tFe in Cfg1O?O O in Cfg1O?O s 0.68 0.66 1.83 0.63 1.83 p 0.69 0.64 4.74 0.67 4.71 d 6.62 6.65 0.00 6.63 0.00 Total 8.00 7.95 6.57 7.94 6.53 Charge 0.00 0.05 ?0.57 0.06 ?0.53 M 2.20 1.82 0.06 2.06 0.00

The above changes of the electron number for O atom and its neighbor Fe atoms in the configurationsandcan be observed directly from Fig.7.The electron density difference map ofplane in the configurationis represented in Fig.7(a).In the electron density difference map ofplane in the configuration,the electronic losses of the Fe atoms for the first nearest neighboring to O atom are significant along the[001]direction because the O–Fe(1nn)distance is 1.77 ?A.However,the electronic losses of the Fe atoms for the second nearest neighboring to O atom are not obvious along the[110]direction because the O–Fe(2nn)distance is 2.00 ?A.The electronic gains of O atom are not obvious in Fig.7(a).The electron density difference map of(001)plane in the configurationis shown in Fig.7(b).In the electron density difference map of(001)plane in the configuration,the electronic losses of the Fe atoms for the first nearest neighboring to O2 and the second nearest neighboring to O1 are significant along the O2–Fe(1nn to O2)and O1–Fe(2nn to O1)direction,respectively. The electronic gains of O atoms are obviously the configurationas shown in Fig.7(b).The gained electrons concentrate between the two O atoms.

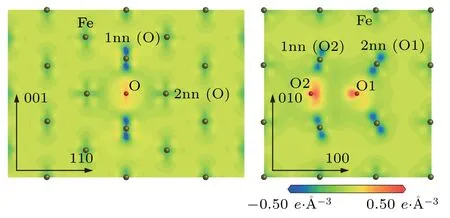
Fig.7.Electron density difference maps of(a)plane in configuration and(b)(001)plane in (a)1nn(O)and 2nn(O)denote the first and second nearest neighboring Fe atoms of O atom.(b)1nn(O2)refers to the first nearest neighboring Fe atom of O2 atom and 2nn(O1)denotes the second nearest neighboring Fe atom of O1 atom.

3.3.Interactions of a vacancy with C and O

When a vacancy is introduced into a bcc Fe cell separately with n(n=1,2,...,6)FIAs(FIA refers to C or O),their corresponding possible configurations are obtained as shown in Fig.8. In these configurations,a vacancy is substituted for the body-centered Fe atom.For n=1,2,...,6,the interactions of a vacancy with n C/O atoms will be discussed below,respectively.

When both an FIA and a vacancy stay in bcc Fe,four configurations are considered as shown in Fig.8 and Table 5.In the configuration,the FIA occupies the first nearest neighbor octahedral interstitial site of the vacancy.There are six equivalent sites in bcc Fe,i.e.,six face-centered sites.In the configurationthe FIA occupies the second nearest neighbor octahedral interstitial site of the vacancy.There are twelve equivalent sites in bcc Fe,i.e.,middle points of twelve edges. In the configurationthe FIA stays in the vacancy.In the configurationthe FIA is midway between the vacancy and its first nearest neighbor Fe atom along the?111?direction.

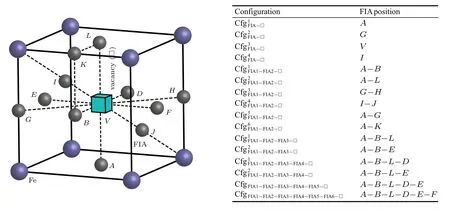
Fig.8.Possible configurations of a vacancy in a bcc Fe cell with n(n=1,2,...,6)FIAs(FIA refers to C or O).

Table 5.Configurations,figures,interaction energy values(in unit eV)and distances of an FIA(FIA refers to C or O)to vacancy in bcc Fe.There are twodistances in units of lattice parameter a0,the first one is that before relaxation,and the second one is that after relaxation.and our interaction energy values are compared with those of Akshay et al.,[76]given after comma.

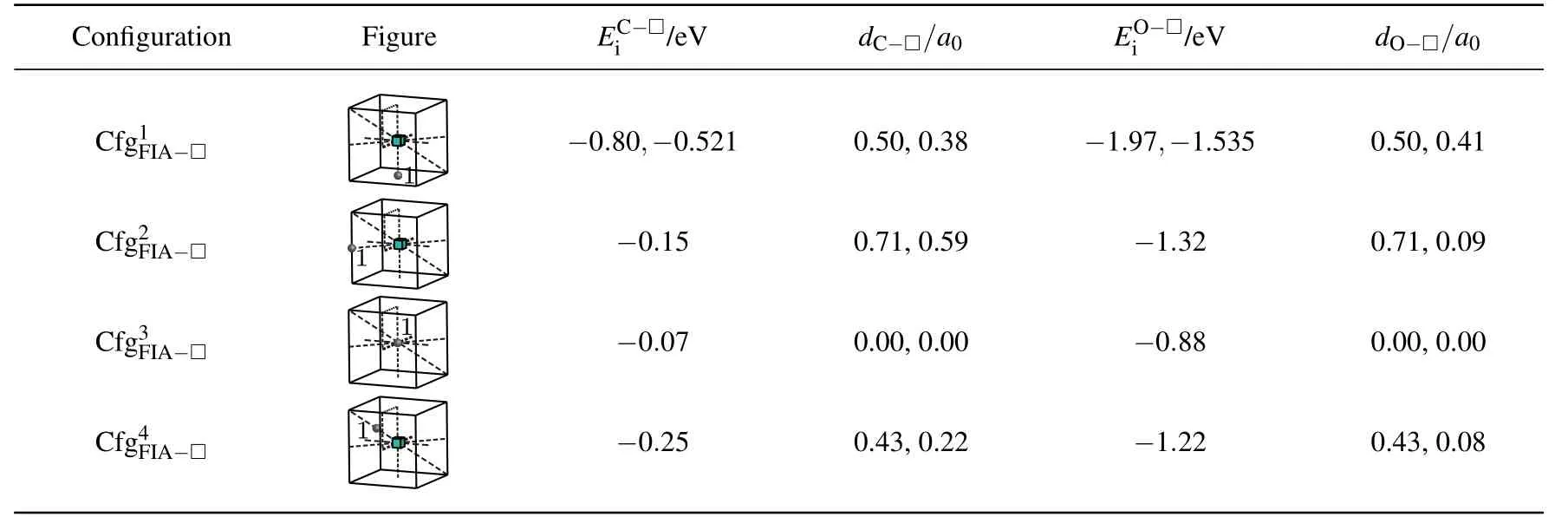
Table 5.Configurations,figures,interaction energy values(in unit eV)and distances of an FIA(FIA refers to C or O)to vacancy in bcc Fe.There are twodistances in units of lattice parameter a0,the first one is that before relaxation,and the second one is that after relaxation.and our interaction energy values are compared with those of Akshay et al.,[76]given after comma.

A vacancy and two FIAs can form six configurations in bcc Fe as shown in Fig.8 and Table 6.The FIA in the first nearest neighboring to vacancy stays preferentially at its first nearest neighbor octahedral interstitial site as shown in the configurationi=1,2,5,and 6. The second FIA is also the first nearest neighbor to the vacancy as shown in the configurationi=1 and 2.In the configurationsandthe two FIAs in the first nearest neighboring to vacancy are aligned along the?110?and?001?directions,respectively.The second FIA stays possibly at the octahedral interstitial site in the second nearest neighboring to vacancy as shown in the configurationsandMoreover,two configurationsandare also considered in our work.In the configurationthe two FIAs are the second nearest neighbors to the vacancy and aligned along thedirection. In the configurationthe two FIAs neighboring to vacancy are aligned along thedirection.

As shown in Table 6,all the interaction energy values of a vacancy with two FIAsare negative.Therefore,a vacancy can attract two C atoms,or two O atoms,or a C atom and an O atom,and they can form stable,andconfigurations.

Nevertheless,the most stable configurations are different forandThe greatest negative interaction energy ?1.83 eV is obtained for the configuration.The configurationis the most stable fori.e.,two C atoms are situated at the first nearest neighbor octahedral interstitial site of the vacancy and aligned along thedirection. The greatest negative interaction energy values ?2.61 eV,?2.61 eV,and ?3.89 eV are obtained forandin the configurationrespectively. The configurationis the most stable for,andi.e.,two FIAs are situated at the first nearest neighbor octahedral site and two sides of the vacancy,and aligned along thedirection.

In Table 7 summarized are the number,population,and length(in unit)of FIA–Fe(FIA is C or O)bonds for each of the configurations,andas shown in Fig.8,Tables 5 and 6.

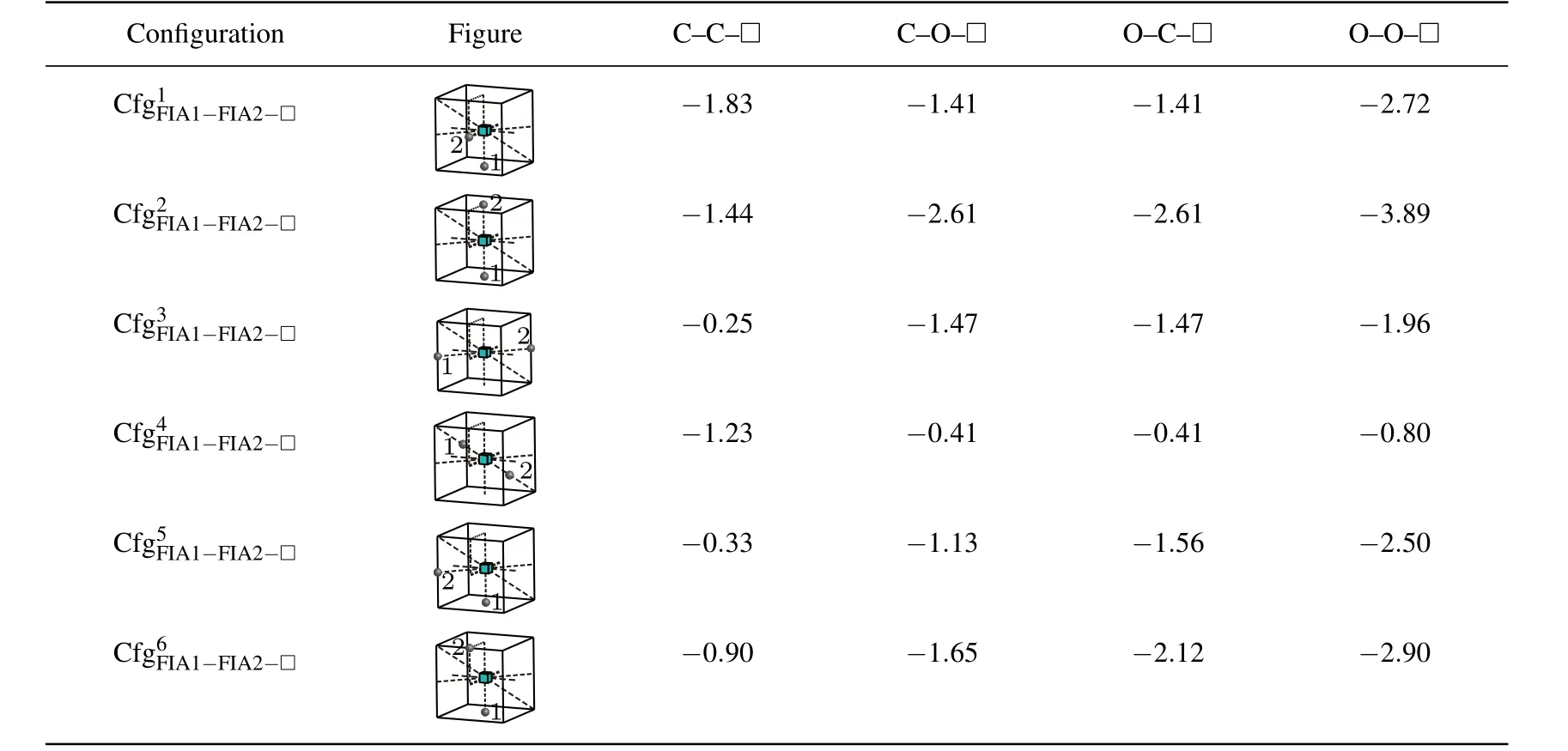
Table 6.Configurations,figures,and interaction energy values(in unit eV)of vacancy with two FIAs for bonds C–C,C–O,and O–O.

Table 7. Number,population,and length(in unit ?A)of FIA–Fe(FIA refers to C or O)bonds in configurations ,andas shown in Fig.8,Tables 5 and 6.

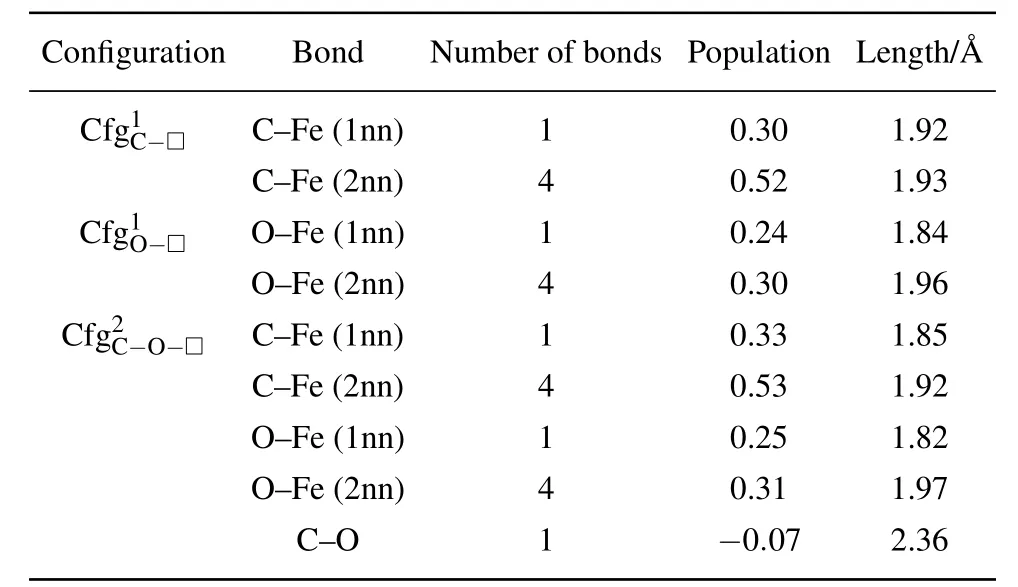
Table 7. Number,population,and length(in unit ?A)of FIA–Fe(FIA refers to C or O)bonds in configurations ,andas shown in Fig.8,Tables 5 and 6.

The properties of FIA–Fe bond in configurationsandare similar,and they have no significant difference.Due to the interaction of C–O in the configuration,the length of C–Fe(1nn)bond shortens from 1.92in the configurationto 1.85 ?A in the configuration

In Table 8 summarized are the electronic distributions in different orbits,the values of charge(e)and magnetic moment(μB)of O atom and its neighbor Fe atom in the configurationsand

For the Fe atom in the first nearest neighboring to O atom in the configurationthe electron numbers in s and p orbits decrease,respectively,from 0.68 to 0.66 in s orbit and from 0.69 to 0.66 in p orbit,the electron number in d orbit increases from 6.62 to 6.69.The total electron number,charge,and magnetic moment of the Fe atom(1nn)are 8.00,0.00,and 2.76μB,respectively.

For the Fe atom in the second nearest neighboring to O atom in the configuration,the electron numbers in s and d orbits decrease,respectively,from 0.68 to 0.60 in s orbit and from 6.62 to 6.61 in p orbit,and the electron number in p orbit increases from 0.69 to 0.71.The total electron number,charge,and magnetic moment of the Fe atom(2nn)are 7.92,0.08,and 4.60μB,respectively.

Table 8.Electronic distributions in different orbits,values of charge(e),and magnetic moment(μB)of O atom and its neighbor Fe atoms in configurations and

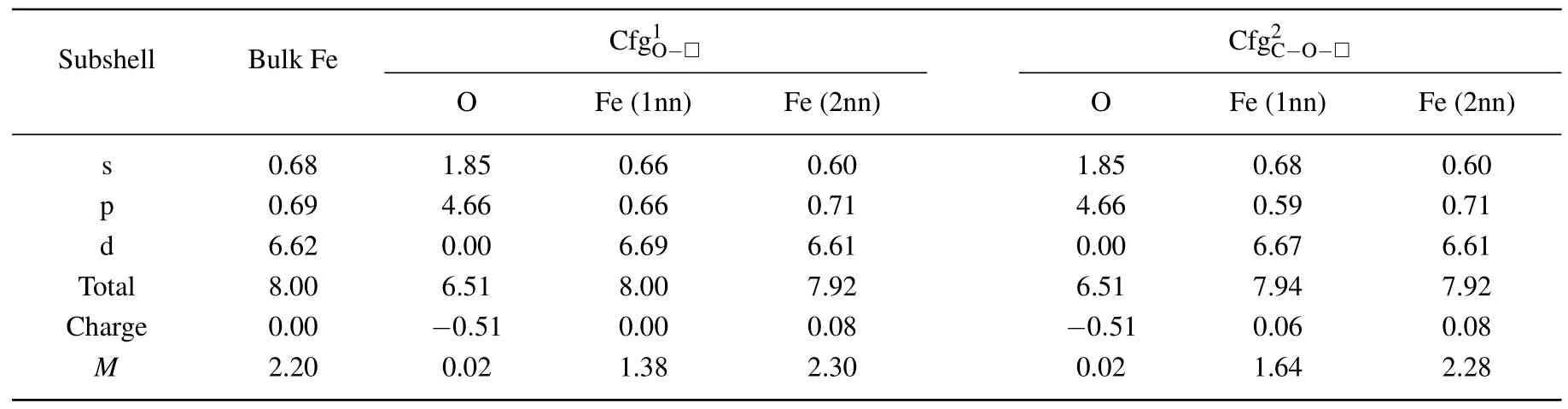
Table 8.Electronic distributions in different orbits,values of charge(e),and magnetic moment(μB)of O atom and its neighbor Fe atoms in configurations and

For the Fe atom in the first nearest neighboring to O atom in the configurationthe electron number in p orbit decreases from 0.69 to 0.59 in p orbit and the electron number in d orbit increases from 6.62 to 6.67.The total electron number,charge,and magnetic moment of the Fe atom(1nn)are 7.94,0.06,and 3.28μB,respectively.

For the Fe atom in the second nearest neighboring to O atom in the configuration,the electron numbers in s and d orbits decrease,respectively,from 0.68 to 0.60 in s orbit,and from 6.62 to 6.61 in p orbit,and the electron number in p orbit increases from 0.69 to 0.71.The total electron number,charge,and magnetic moment of the Fe atom(2nn)are 7.92,0.08,and 4.56μB,respectively.

The changes of electronic distribution around C/O and its neighbor Fe atoms in the configurationsandcan be observed from electron density difference maps.The electron density difference maps ofplane in the configurationsandare represented in Fig.9.

As shown in Figs.9(a)–9(c),the changes of electronic density around C/O and its neighbor Fe atoms in the configurationare very similar to those in the configurationsand. Thedistance is 0.42 a0in the configuration,which is subtly greater than that(0.41 a0)in the configuration.Thedistance is also 0.42 a0in the configurationwhich is slightly greater than that(0.38 a0)in the configurationThe electronic distribution around O atom is significantly different from that around C atom.The electronic distribution around the O atom is localized and looks like a“diamond ring”.The electronic density is significantly greater in the part of“diamond”than in the other parts of the“diamond ring”.The electronic distribution around the C atom is non-localized and relatively uniform between the C atom and its neighbor Fe atoms.

According to the above calculations,one or two FIAs neighboring to a vacancy preferentially occupy the first nearest neighbor,octahedral site,as shown in the configurationand are aligned in the?110?in the configurationor the?001?direction in the configurationsandWhen the third FIA is incorporated into bcc Fe with a vacancy,it also occupies the first nearest neighbor,octahedral site,of the vacancy,thus possibly forming two configurations as shown in Fig.8 and Table 9. The three FIAs around the vacancy stay on the plane{100}in the configurationor{111}in the configurationIn the configurationthe sites marked as 1 and 3 are equivalent to each other. In the configuration,all the three sites denoted as 1,2,and 3 are equivalent to each other.

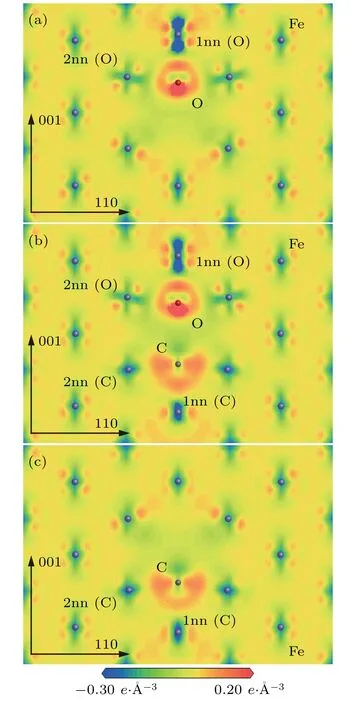
Fig.9.Electron density difference maps ofplane in configurations(a)and.1nn(FIA)and 2nn(FIA)refer to the first and second nearest neighboring Fe atoms of FIA(FIA represents C or O)atom.

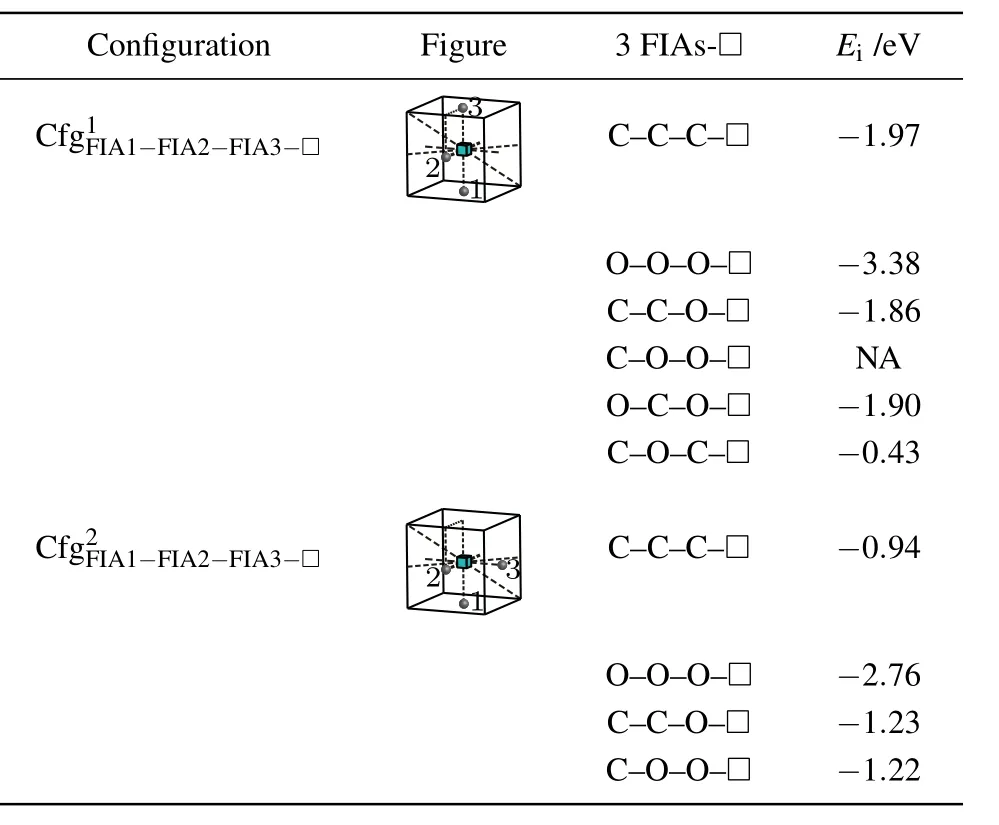
Table 9. Configurations,figures,and interaction energy values of a vacancy with 3 FIAs.NA,whose value is not shown here,denotes corresponding unstable configuration.

For a vacancy,two C atoms and an O atom in bcc Fe,three configurationsandare considered as shown in Table 9.The greatest negative interaction energy ?1.86 eV is obtained,i.e.,is the most stable configuration,and can be formed.

Similarly,for a vacancy,a C atom and two O atoms in bcc Fe,three configurationsandare considered as shown in Table 9.The configurationis unstable,the O atom at the site marked as 3 goes farther away from the octahedral interstitial site.The greatest negative interaction energy ?1.90 eV is obtained,i.e.,is the most stable configuration,and can be formed.

Consequently,a vacancy and three FIAs prefer to stay on a plane{010}for,and O–in the configurationas shown in Fig.8 and Table 9.

When the fourth FIA is introduced into the configurationthe two configurationsandare possibly formed as shown in Fig.8 and Table 10.

For a vacancy and 4C atoms in bcc Fe,the two configurationsandare considered.A positive interaction energy 0.53 eV is obtained for the configurationi.e.,this configuration is not stable and cannot be formed.The configurationhas negative interaction energy ?1.40 eV,i.e.,it is stable and possibly formed.Therefore,a vacancy can attract four C atoms and forms the configurationas shown in Fig.8 and Table 10.

For a vacancy and 4O atoms in bcc Fe,two configurations having the same bond asare also calculated.Nevertheless,the results are different.Two negative interaction energy values ?0.86 eV and ?2.79 eV are obtained for the configurationsandi.e.,the two configurations are stable and formed possibly.A vacancy can attract four O atoms and form a more stable configuration

For the case where a vacancy,three C atoms,and an O atom approach to each other in bcc Fe,three configurations are considered as shown in Table 10. The configurationis unstable,the O atom goes farther away from the octahedral interstitial site. Two negative interaction energy values(?0.75 eV for,and?0.15 eV for)are obtained. That is,the two configurations are formed possibly,yet the configurationis a more stable configuration.

For the case where a vacancy,three O atoms and a C atom approach to each other in bcc Fe, three configurations are considered as shown in Table 10. A positive and two negative interaction energy values(0.44 eV for?1.02 eV forand?0.97 eV for)are obtained.That is,the configurationis not stable and cannot be formed.The other two configurations are formed possibly,yet the configurationis the most stable configuration.

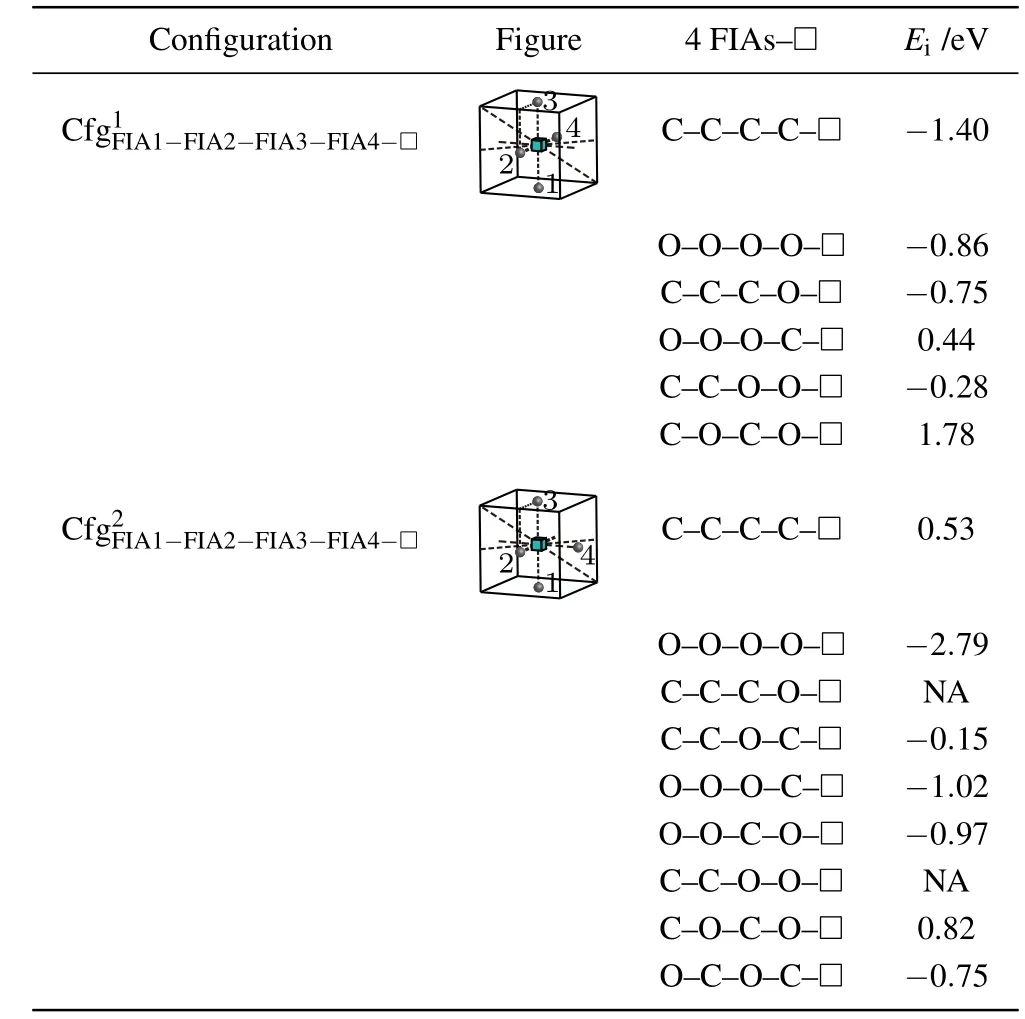
Table 10.Configurations,figures,and interaction energy values of a vacancy with 4 FIAs in bcc Fe.NA,whose values are not shown here,denotes unstable corresponding configuration.

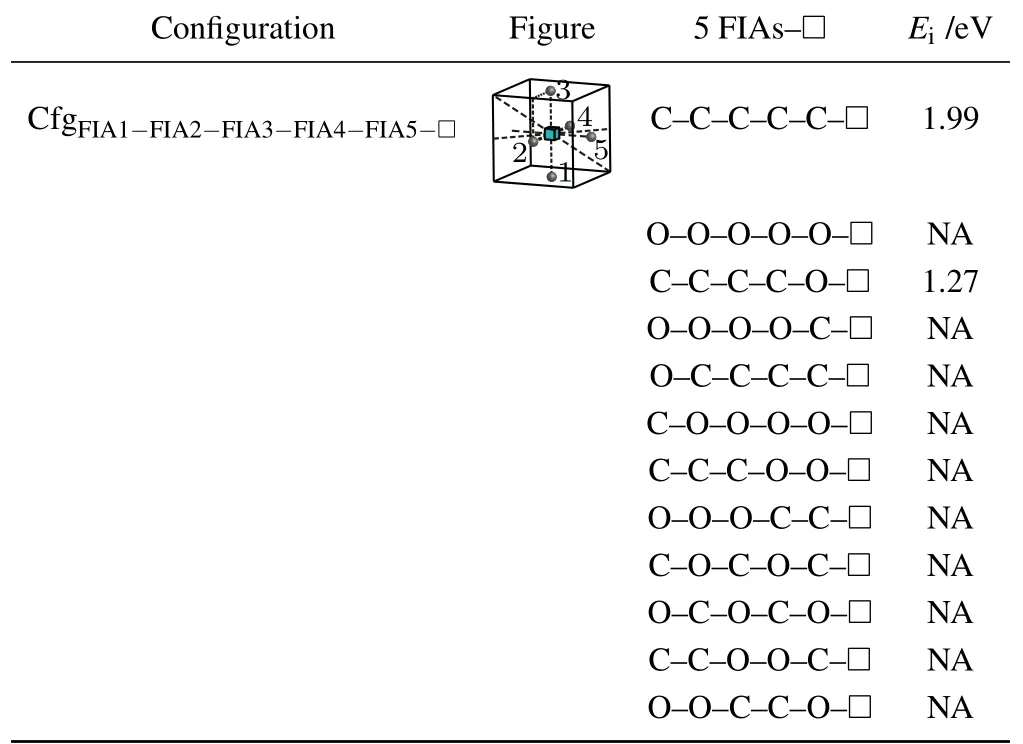
Table 11.Configuration,figure,and interaction energy values of a vacancy with 5 FIAs in bcc Fe. NA,whose values are not shown here,denotes corresponding unstable configuration.

For the case where a vacancy,two C atoms,and two O atoms approach to each other in bcc Fe,five configurations are considered as shown in Table 10. The configurationis unstable,two C atoms go farther away from the octahedral interstitial site. Four interaction energy values(?0.28 eV for,1.78 eV for,0.82 eV forand ?0.75 eV for)are obtained.That is,the two configurationsandare not stable and cannot be formed. The other two configurations are formed possibly,yet the configurationis more stable.

For a vacancy and five FIAs in bcc Fe,a configurationis considered in this work as shown in Fig.8 and Table 11.

Two positive interaction energy values(1.99 eV for the configurationand 1.27 eV for the configuration)are obtained,which indicates repulsive interactions between the five FIAs and the vacancy.For our considered other 10 configurations of a vacancy and five FIAs in bcc Fe,they are unstable and cannot be formed.During the relaxations of the 10 configurations,some of the five FIAs go farther away from the octahedral interstitial sites.

For a vacancy and six FIAs in bcc Fe,a configurationis considered in this work as shown in Fig.8 and Table 12.

Table 12.Configuration,figure,and interaction energy values of a vacancy with 6 FIAs in bcc Fe.NA,whose values are not shown here,denotes corresponding unstable configuration.

Five positive interaction energy values(3.14 eV for the configuration, 5.15 eV for the configuration7.28 eV for the configuration8.49 eV for the configurationand 4.08 eV for the configurationare obtained,which indicates repulsive interactions between the six FIAs and the vacancy. For our considered other 3 configurations of a vacancy and six FIAs in bcc Fe,they are unstable and cannot be formed.During the relaxations of the 3 configurations,some of the six FIAs go farther away from the octahedral interstitial sites.

Interaction energy values of a vacancy with n(n=1,2,...,4)FIAs(FIA refers to C or O)are summarized in Fig.10,in which included are the most possibly formedconfigurations in bcc Fe.

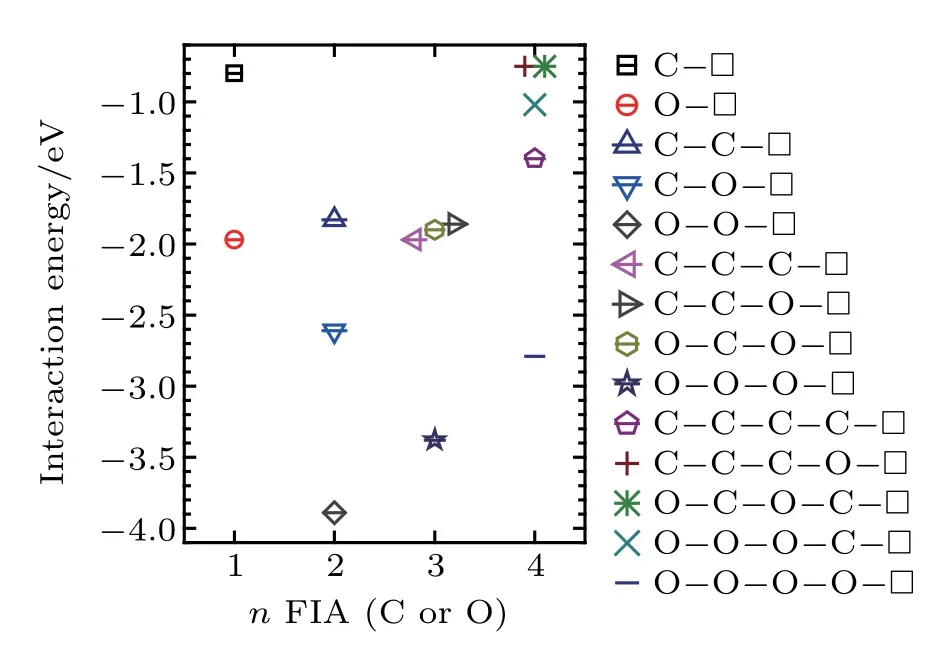
Fig.10.Interaction energy values of a vacancy in a bcc Fe with n(n=1,2,3,and 4)FIAs(FIA refers to C or O).

When n=1,a vacancy and an FIA can form a stable configurationwith interaction energy value of?0.80 eV forand ?1.97 eV forIn the configurationthe FIA stays in the first nearest neighbor,octahedral interstitial site of the vacancy.

When n=2,a vacancy and two FIAs can form stable configurations,which arewith interaction energy of ?1.83 eV,with interaction energy of ?2.61 eV,andwith interaction energy of ?3.89 eV,respectively.When a C atom is incorporated into the configurationthe configurationcan be formed,and is the most stable in our consideredconfigurations.In the configurationthe two C atoms stay at the first nearest neighboring octahedral interstitial site of the vacancy and are aligned along the?110?direction.Theinteraction energy(?1.83 eV)in the configurationis less than twointeraction enegy value(?0.80×2=?1.60 eV)inA configurationis more stable than two configurationsWhen an O atom is incorporated into the configurationthe configurationcan be formed,and is the most stable in our consideredconfigurations.In the configurationthe two O atoms stay at the first nearest neighboring octahedral interstitial site of the vacancy,and are aligned along the?001?direction.Theinteraction energy(?3.89 eV)inis greater than twointeraction energy values(?1.97×2=?3.94 eV)inTwo configurationsare more stable than a configuration.When an O atom is incorporated into the configurationor a C intothe configurationcan be formed,and is the most stable in our consideredconfigurations.In the configuration,a C and an O atom stay at the first nearest neighboring octahedral interstitial site of the vacancy and are aligned along the?001?direction.interaction energy(?2.61 eV)in the configurationis greater thanandinteraction energy values(?0.80+?1.97=?2.77 eV)in the configurationTwo configurationsandare more stable than a configuration.Except forall bigcomplexes are less stable than small

When n=3,a vacancy and three FIAs can form stable configurations,which arewith interaction energy of ?1.97 eV,with interaction energy of?3.38 eV,with interaction energy of ?1.86 eV,andwith interaction energy of ?1.90 eV,respectively.In the configuration,the vacancy and the three FIAs in the first nearest neighboring to the vacancy stay on the plane{010},and the two FIAs marked as FIA1 and FIA3 are equivalent to each other.

When n=4,a vacancy and four FIAs can form stable configurations,which arewith interaction energy value of ?1.40 eV,with interaction energy value of ?2.79 eV,with interaction energy value of ?0.75 eV,of ?1.02 eV,andwith interaction energy value of ?0.75 eV,respectively. In the configurationsandthe vacancy and the four FIAs in the first nearest neighboring to the vacancy stay on the plane{010}.In the configuration,the four FIAs are all the first nearest neighbors of the vacancy,and theline is perpendicular to the plane of

In Subsections 3.2 and 3.3,the interactions of O–C andare obtained.Accordingly,to study the migration of O in bcc Fe in the presence of C and vacancy,the O–C andinteraction should be taken into consideration.

4.Conclusions

In this work,the behaviors of a single FIA(foreign interstitial atom,i.e.,C or O)in bcc Fe and interactions of FIA1–FIA2 and oxygen–carbon–vacancy are calculated by first principles calculations based on the density functional theory.

Octahedral interstitial site is the most stable position for an O atom in bcc Fe.A C atom in bcc Fe is more stable than an O atom in bcc Fe.Migration energy of an O atom in bcc Fe obtained from the method of transition state search(TSS)is 0.46 eV.The most possible migration path of an O atom in bcc Fe is from one octahedral interstitial site to its first nearest neighbor octahedral interstitial site,in which a tetrahedral site is just in the middle between the two sites.The strengths of FIA–Fe(1nn)bonds(0.50 for C and 0.32 for O)are greater than that of the Fe–Fe metallic bond(0.26).The strength of the material is enhanced after a small number of C or O atoms are incorporated into iron-based alloy and a dilute solid solution is formed.And the strengthening effect of C atom is more significant than that of O atom.The length of O–Fe bond is greater than that of C–Fe bond.

The interaction energy values for C–C,O–O,and C–O complex are all positive,which implies the repulsive interaction of C–C,O–O,and C–O in bcc Fe with different reconfigurations.The repulsion is the greatest in C–O,is the smallest in O–O,is in the middle in C–C.As the FIA1–FIA2 distance is less than a0before relaxation,the FIA1–FIA2 distance becomes greater after relaxation.Compared with the DOS of Fe atom in bcc Fe without O atom,the DOS of the Fe atom first nearest neighboring to O has the changes as follows.(i)An obvious depletion for the highest peak is existent.(ii)Two hybridizations occur.In the configuration of O–O complex,each hybridization peak of DOS for O atom is split into two parts.

When the concentration of FIA(FIA refers to C or O)is relatively high,a vacancy can attract four FIAs and form stablecomplex.Except forall bigcomplexes are less stable than smallThe most stable position of a C or O atom around a vacancy is the first nearest neighbor octahedral interstitial site of the vacancy.The FIA–attraction makes the distance between both smaller,i.e.,it shortens from 0.50 a0to 0.38 a0forand to 0.41 a0for O–In the most stable configuration ofcomplex,two C atoms are situated at the first nearest neighbor octahedral interstitial site of the vacancy,and aligned along the?110?direction.In the most stable configuration oforcomplex,two FIAs are situated at the first nearest neighbor octahedral site and two sides of the vacancy,and aligned along the?001?direction.In the most stable configuration ofcomplex,the electronic distribution around O atom is localized and looks like a“diamond ring”.The electronic density is significantly greater in the part of“diamond”than in other parts of the“diamond ring”.The electronic distribution around C atom is non-localized and relatively uniform between the C atom and its neighbor Fe atoms.