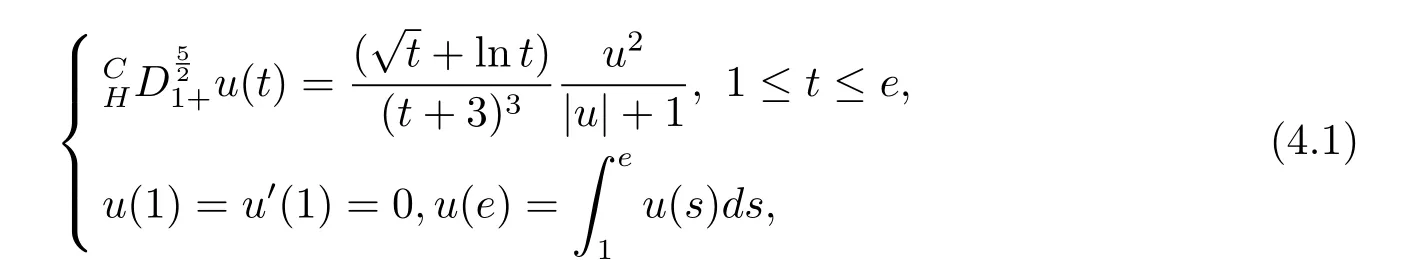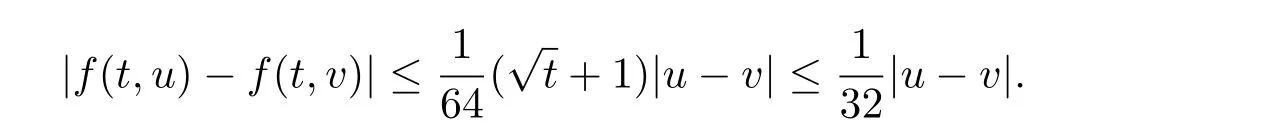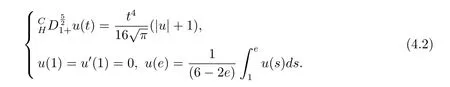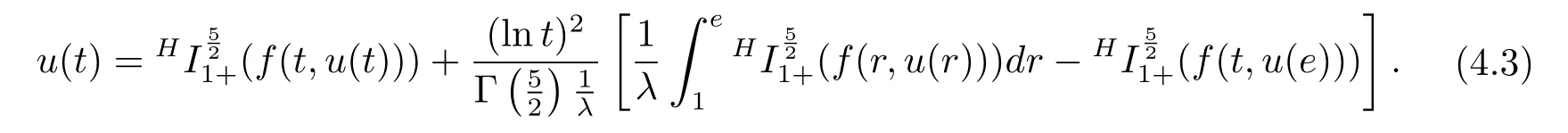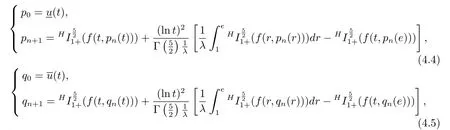EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR CAPUTO-HADAMARD TYPE FRACTIONAL DIFFERENTIAL EQUATIONS
SHI Lin-fei,LI Cheng-fu
(School of Mathematics and Computational Science,Xiangtan University,Xiangtan 411105,China)
Abstract:In this paper,we study a class of Caputo-Hadamard fractional differential equations with boundary value problems. By using Banach fixed point theorem and the method of upper and lower solutions method,the existence and uniqueness results of the solutions are obtained,which generalizes some results about ordinary differential equations with boundary value problems.As an application,two examples are given to illustrate our main results.
Keywords: fractional differential equations;Caputo-Hadamard derivatives;Banach fixed point theorem;upper and lower solutions method
1 Introduction
Over the past few decades,the fractional calculus made great progress,and it was widely used in various fields of science and engineering. There were numbers applications in electromagnetics,control theory,viscoelasticity and so on.There was a high-speed development in fractional differential equations in recent years,and we referred the reader to the monographs Podlubny[1],Kilbas et al.[2]and Zhou[3].In the current theory of fractional differential equations,much of the work is based on Riemann-Liouville and Caputo fractional derivatives,but the research of Caputo-Hadamard fractional derivatives of differential equations is very few,which includes logarithmic function and arbitrary exponents.Motivated by this fact,we consider a class of Caputo-Hadamard fractional differential equations with boundary value problems(BVPs).
Nowadays,some authors studied the existence and uniqueness of solutions for nonlinear fractional differential equation with boundary value problems.For the recent development of the topic,we referred the reader to a series papers by Ahmad et al.[4–6],Mahmudov et al.[7]and the references therein.Details and properties of the Hadamard fractional derivative and integral can be found in[8–12].
Wafa Shammakh[13]studied the existence and uniqueness results for the following three-point BVPs
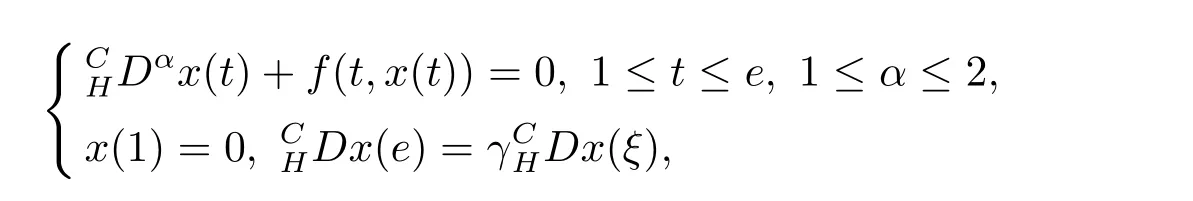
Yacine Arioua and Nouredine Benhamidouche[14]studied the existence of solutions for the following BVPs of nonlinear fractional differential equations
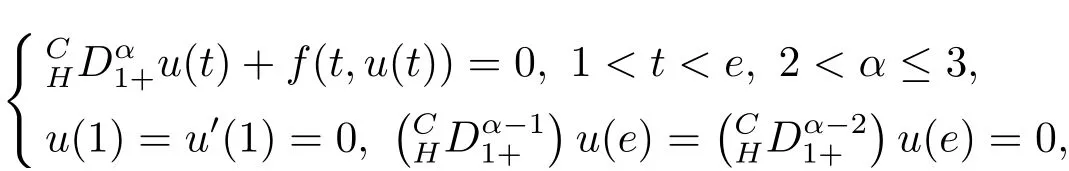
Yunru Bai and Hua Kong[15]used the method of upper and lower solutions,proved the existence of solutions to nonlinear Caputo-Hadamard fractional differential equations
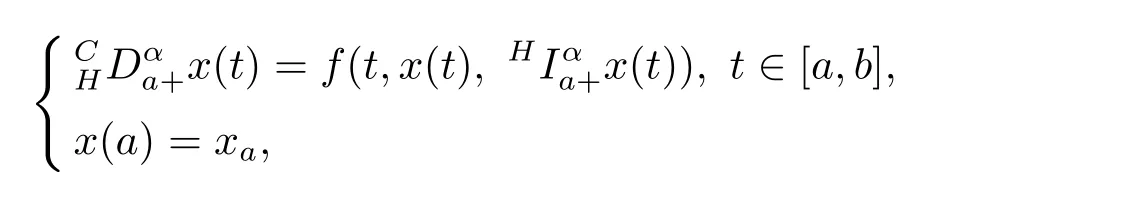
The purpose of this paper is to discuss the existence and uniqueness of solutions for nonlinear Caputo-Hadamard fractional differential equations
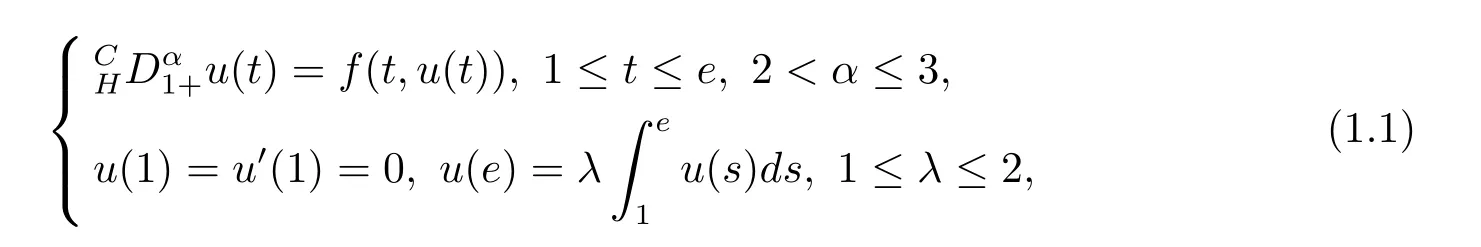
2 Preliminaries
In this section,we introduce some necessary definitions,lemmas and notations that will be used later.
Definition 2.1[2]The Hadamard fractional integral of order α ∈R+for a continuous function g:[1,∞)→R is given by
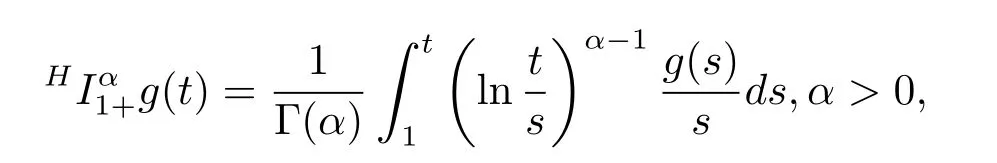
where Γ(·)stands for the Gamma function.
Definition 2.2[2]The Hadamard fractional derivative of order α ∈R+for a continuous function g:[1,∞)→R is given by
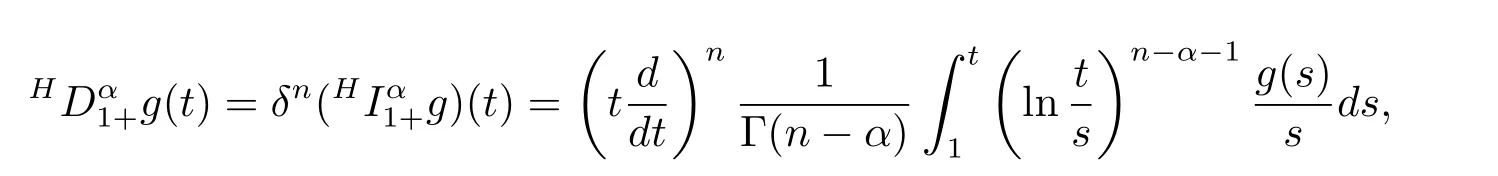
where n?1<α Definition 2.3[16,17]The Caputo-Hadamard fractional derivative of order α ∈R+for at least n-times differentiable function g:[1,∞)→R is defined as Lemma 2.4[16,17]Let([1,e],R),then Lemma 2.5Let h ∈C([1,e],R),u ∈([1,e],R). Then the unique solution of the linear Caputo-Hadamard fractional differential equation is equivalent to the following integral equation ProofIn view of Lemma 2.4,applyingto both sides of(2.2), where c0,c1,c2∈R. The boundary condition u(1)=u'(1)=0 implies that c0=c1=0.Thus Substituting(2.5)in(2.4),we obtain(2.3).This completes the proof. Based on Lemma 2.5,the solution of problems(1.1)–(1.2)can be expressed as Let E:=C([1,e],R)be the Banach space of all continuous functions from[1,e]to R with the normDue to Lemma 2.5,we define an operator A:E →E as It should be noticed that BVPs(1.1)has solutions if and only if the operator A has fixed points. First,we obtain the existence and uniqueness results via Banach fixed point theorem. Theorem 3.1Assume that f:[1,e]×R →R is a continuous function,and there exists a constant L>0 such that (H1)|f(t,u)?f(t,v)|≤L|u ?v|,?t ∈[1,e],u,v ∈R.If then problem(1.1)has a unique solution on[1,e]. ProofDenotewe set Br:={u ∈C([1,e],R):u≤r}and choosewhere Obviously it is concluded that which implies that ABr?Br.Let u,v ∈Br,and for each t ∈[1,e],we have Therefore, From assumption(3.2),it follows that A is a contraction mapping.Hence problem(1.1)has a unique solution by using Banach fixed point theorem.This completes the proof. Next,we will use the method of upper and lower solutions to obtain the existence result of BVPs(1.1). Definition 3.2Functionsare called upper and lower solutions of fractional integral equation(2.6),respactively,if it satisfies for any t ∈[1,e], Define Theorem 3.3Let f ∈C([1,e]×R,R). Assume that∈C([1,e],R)are upper and lower solutions of fractional integral equation(2.6)withfor t ∈[1,e]. If f is nondecreasing with respect to u that is f(t,u1)≤f(t,u2),u1≤u2,then there exist maximal and minimal solutionsinmoreover,for each,one has ProofConstructing two sequences{pn},{qn}as follows This proof divides into three steps. Step 1Finding the monotonicity of the two sequences,that is,the sequences{pn},{qn}satisfy the following relation for t ∈[1,e]. First,we verify that the sequence{pn}is nondecreasing and satisfies Since f is nondecreasing respect to the second variable,this implies that This deduces Therefore,we assume inductively In view of definition of{pn},{qn},we have By means of the monotonicity of f,it is obvious that We show that Analogously,we easily conclude from the monotonicity of f with respect to the second variables that In a similar way,we know that the sequence{qn}is nonincreasing. Step 2The sequences constructed by(3.3),(3.4)are both relatively compact in C([1,e],R). According to that f is continuous and∈C([1,e],R),from Step 1,we have{pn}and{qn}also belong to C([1,e],R).Moreover,it follows from(3.5)that{pn}and{qn}are uniformly bounded. For any t1,t2∈[1,e],without loss of generality,let t1≤t2,we know that approaches zero as t2?t1→0,where W>0 is a constant independent of n,t1and t2,|f(t,pn(t))|≤W. It implies that{pn}is equicontinuous in C([1,e],R). By Arzelà-Ascoli theorem,we imply that{pn}is relatively compact in C([1,e],R). In the same way,we conclude that{qn}is also relatively compact in C([1,e],R). Step 3There exist maximal and minimal solutions in The sequences{pn}and{qn}are both monotone and relatively compact in C([1,e],R)by Step 1 and Step 2. There exist continuous functions p and q such that pn(t)≤p(t)≤q(t)≤qn(t)for all t ∈[1,e]and n ∈N. {pn}and{qn}converge uniformly to p and q in C([1,e],R),severally.Therefore,p and q are two solutions of(2.6),i.e., for t ∈[1,e].However,fact(3.5)determines that Finally,we shall show that p and q are the minimal and maximal solutions inrespectively.For anythen we have Because f is nondecreasing with respect to the second parameter,we conclude Taking limits as n →∞into the above inequality,we have which means that uL=p and uM=q are the minimal and maximal solutions inThis completes the proof. Theorem 3.4Assume that assumptions of Theorem 3.3 are satisfied.Then fractional nonlinear differential equation(1.1)has at least one solution in C([1,e],R). ProofBy the hypotheses and Theorem 3.3,we inductthen the solution set of fractional integral equation(2.6)is nonempty in C([1,e],R). It follows from the solution set of(2.6)together with Lemma 2.5 that problem(1.1)has at least one solution in C([1,e],R).This completes the proof. In this section,we present two examples to explain our main results. Example 1Consider the following nonlinear Caputo-Hadamard fractional differential equation Therefore LQ<1.Thus all conditions of Theorem 3.1 satisfy which implies the existence of uniqueness solution of the the boundary value problem(4.1). Example 2Consider the problem ProofWheret ∈[1,e],f is continuous and nondecreasing with respect to u.Thus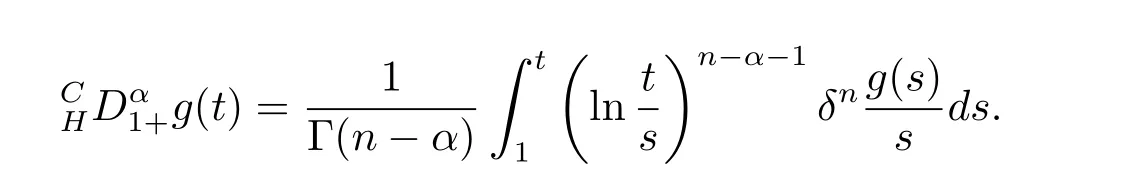
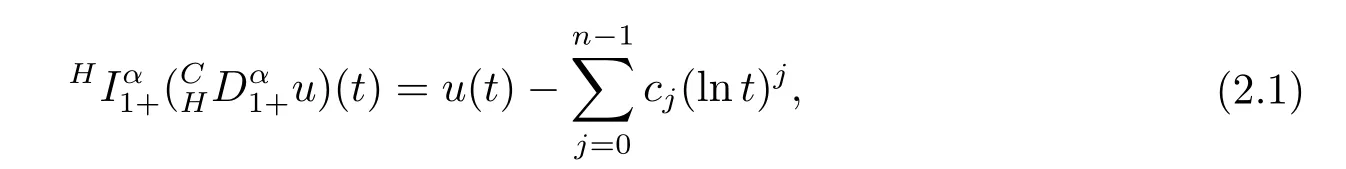
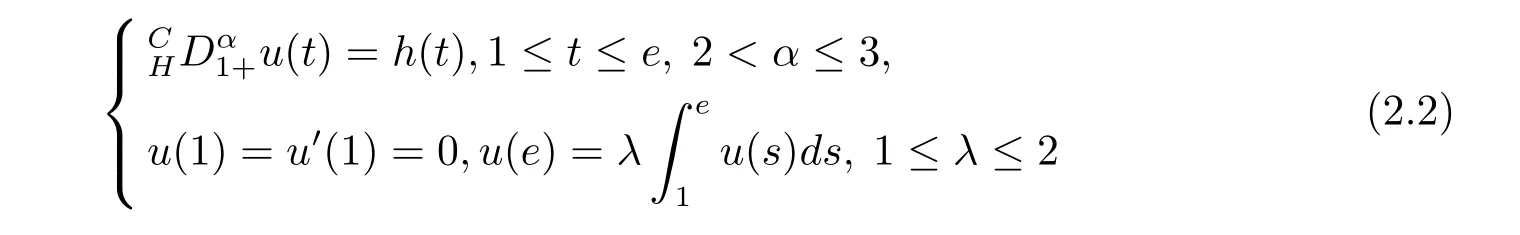
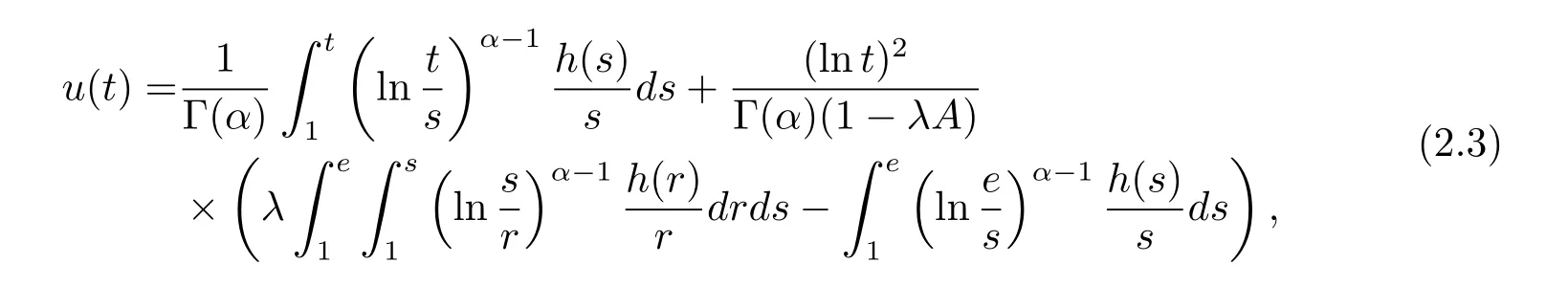


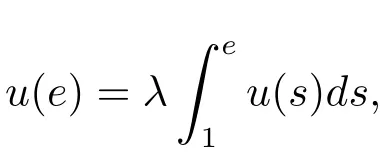
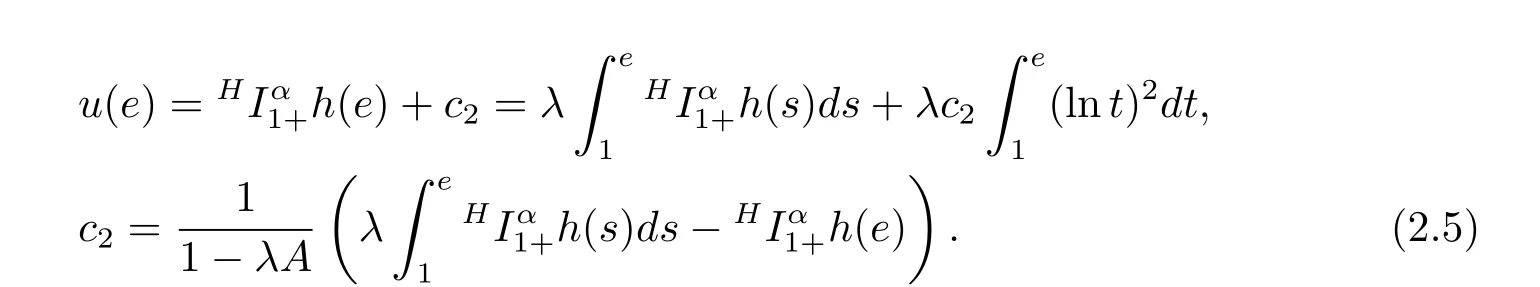
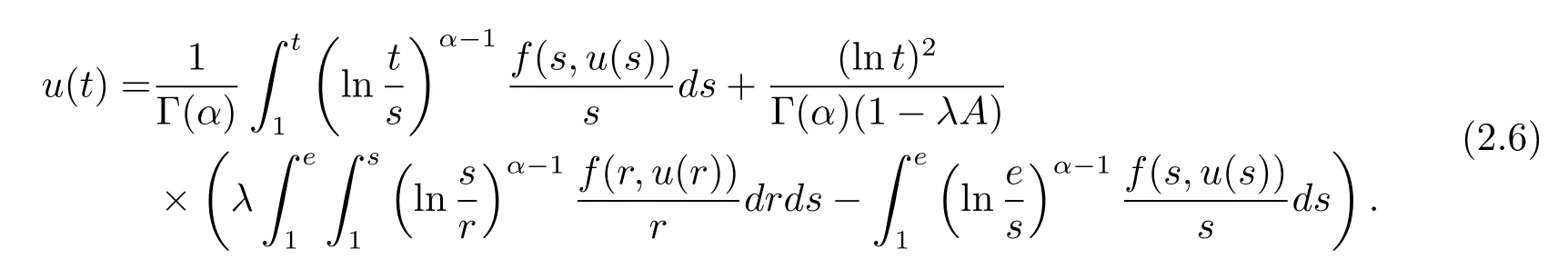
3 Main Results
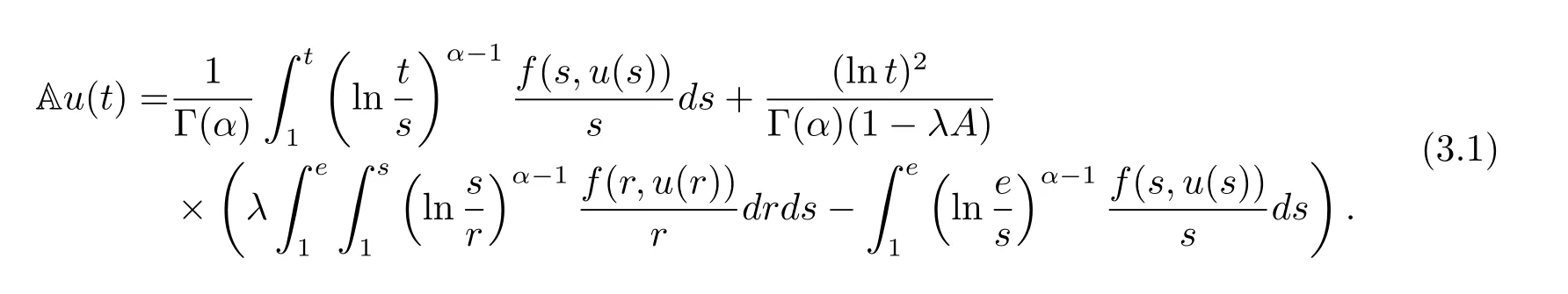
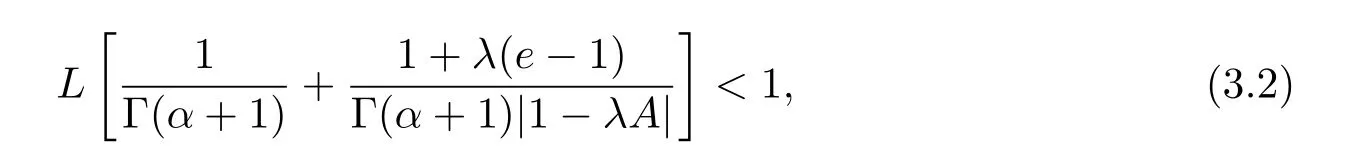
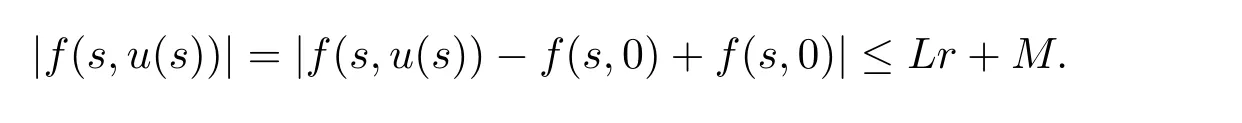
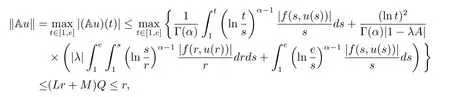
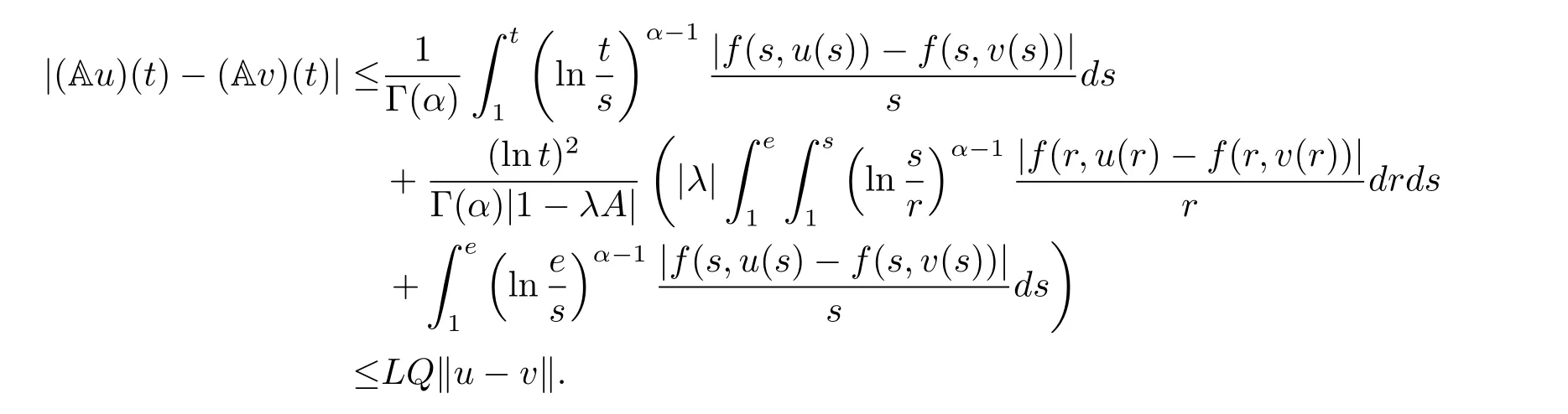
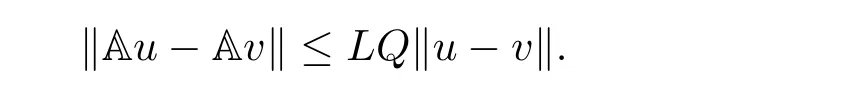
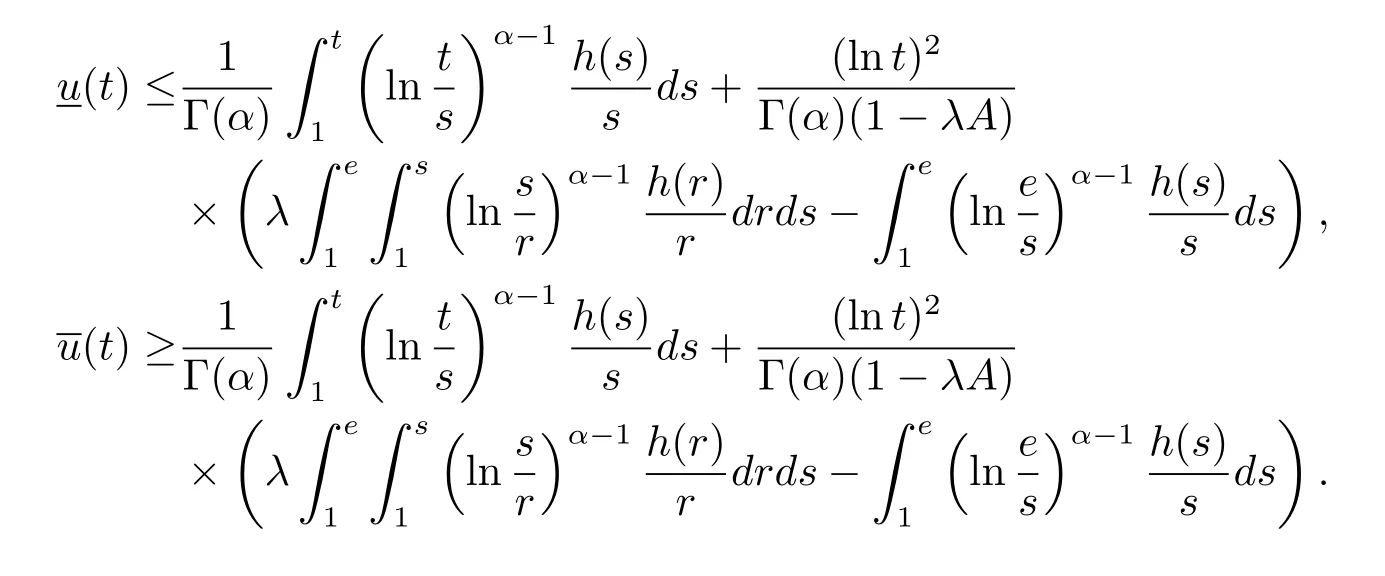
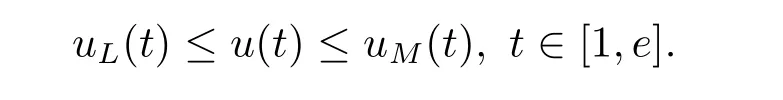
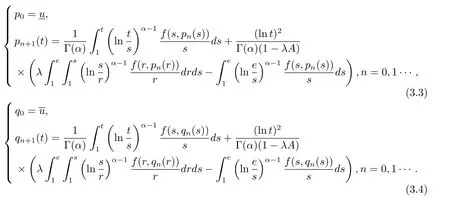
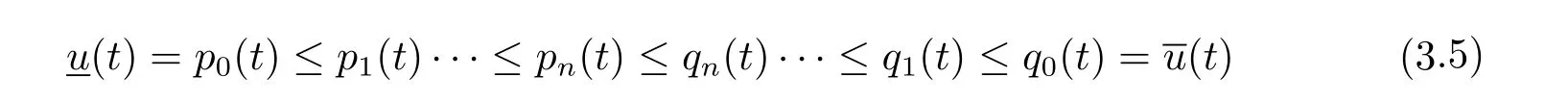
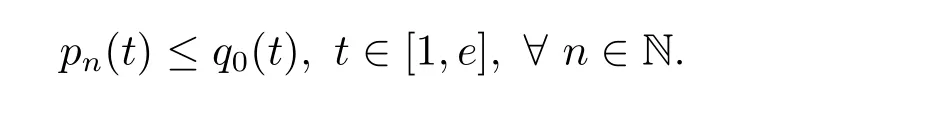
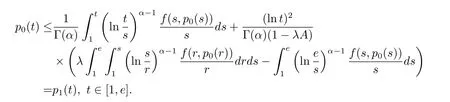
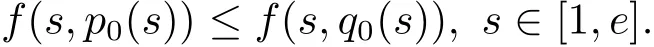
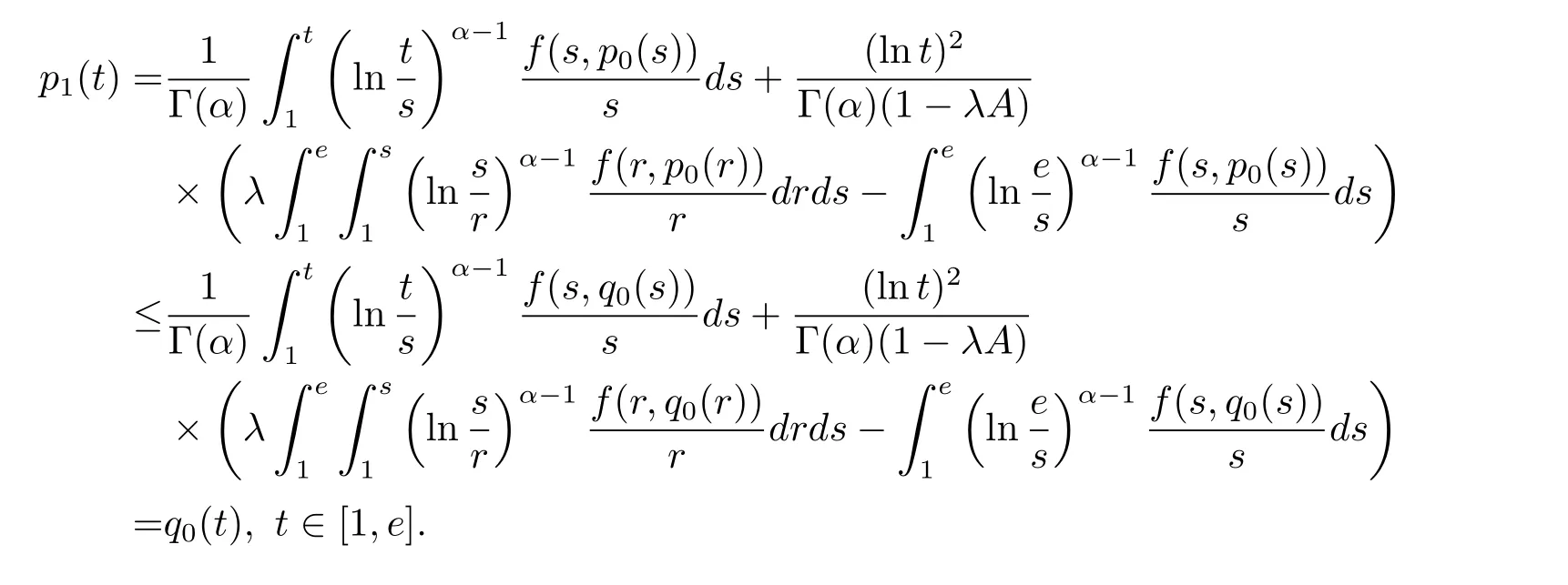

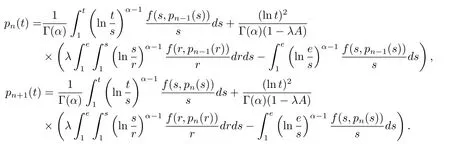
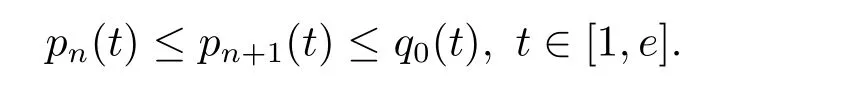
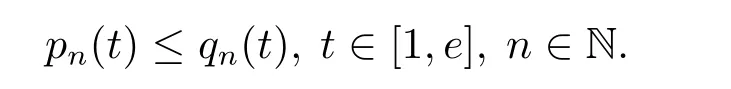
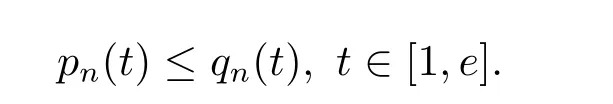
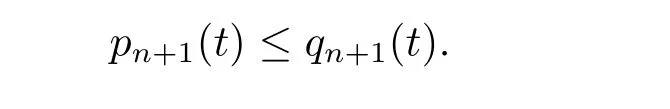

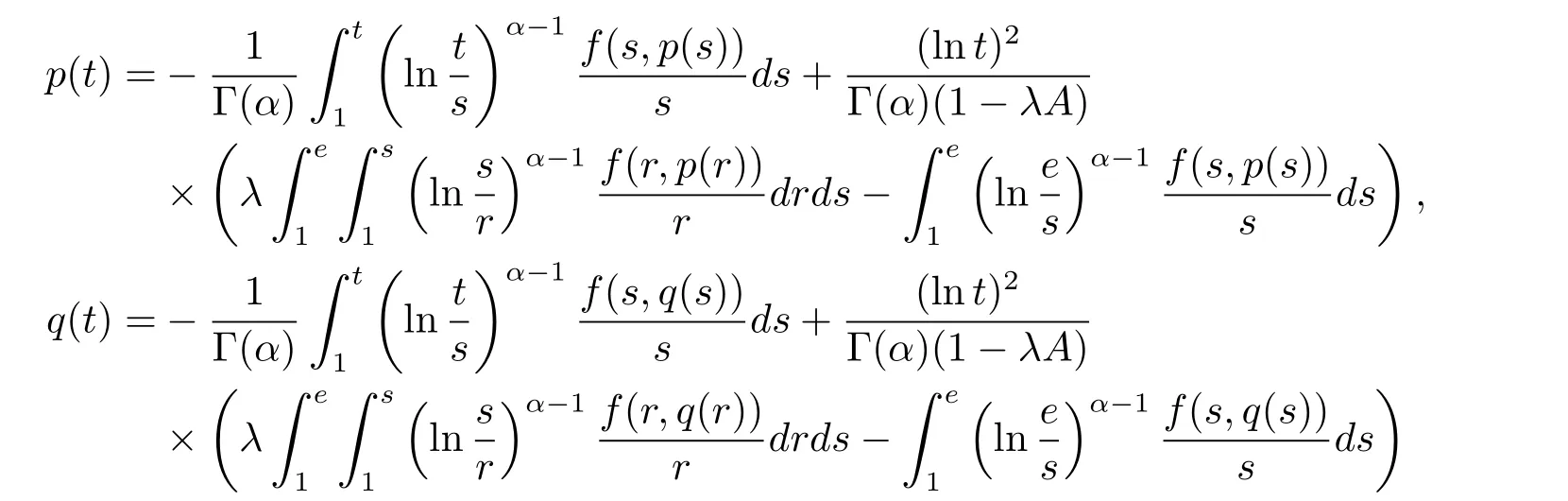
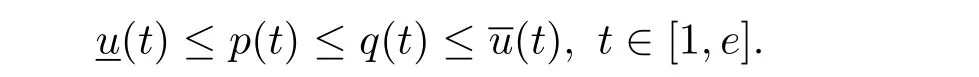
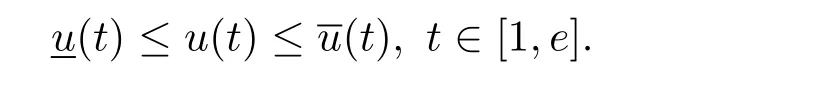
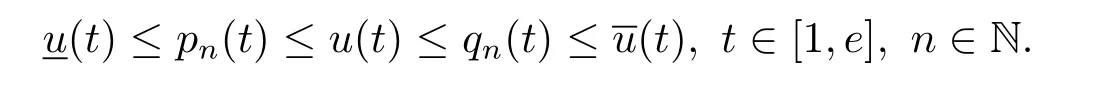
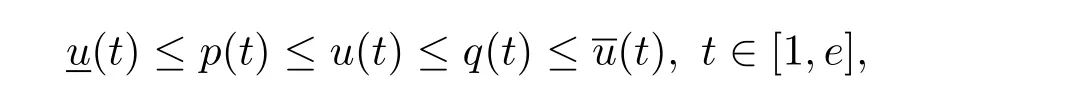
4 Examples