Analysis on Lump,lumpoffand Rogue Waves with Predictability to a Generalized Konopelchenko-Dubrovsky-Kaup-Kupershmidt Equation?

Wen-Hao Liu(劉文豪),Yu-Feng Zhang(張玉峰), and Dan-Dan Shi(石丹丹)

School of Mathematics,China University of Mining and Technology,Xuzhou 221116,China

AbstractIn this paper,we investigate a(2+1)-dimensional generalized Konopelchenko-Dubrovsky-Kaup-Kupershmidt equation.The lump waves,lumpoffwaves,and rogue waves are presented based on the Hirota bilinear form of this equation.It is worth noting that the moving path as well as the appearance time and place of the lump waves are given.Moreover,the special rogue waves are considered when lump solution is swallowed by double solitons.Finally,the corresponding characteristics of the dynamical behavior are displayed.

Key words:Konopelchenko-Dubrovsky-Kaup-Kupershmidt equation,lump waves,lumpoffwaves,rogue waves

1 Introduction

The study of nonlinear science has emerged as a powerful tool to understanding of many natural phenomena.In the past few decades,the soliton solutions have attracted more and more scholars’attention due to their crucial role in many branches of physics and engineering.Especially in Bose-Einstein condensations(BECs),nonlinear control, fluid dynamics and so on.[1?7]In recent years,the solitons and other related issues of nonlinear evolution equations(NLEEs)have become a hot topic.[8?11]It is worth noting that lump waves have been found by many researchers.Many methods to obtain soliton solutions of NLEEs are proposed with the deepening of research,[12?13]such as Hirota bilinear method,[14]inverse scattering transformation,[15]Darboux transformation(DT).[16]Lump waves can be observed in many fields,among which oceanics and nonlinear optics are the most common.[17?19]Numerous theoretical and experimental studies of lump waves are mentioned.[20?24]

In this paper,we consider the following(2+1)-dimensional generalized Konopelchenko-Dubrovsky-Kaup-Kupershmidt(gKDKK)equation[25]

where the coefficients hi(i=1,2,...,8)are the real parameters.When different special coefficient of hiare chose,the Bogoyavlensky-Konoplechenko equation,[26]the isospectral BKP equation[27]and the(2+1)-dimensional Sawada-Kotera equation[28]can be obtained,respectively.

It is no exaggeration to say that many physical phenomena can be described by Eq.(1).The(2+1)-dimensional gKDKK equation was investigated as long ago as 2016 by Feng,[25]and it is pointed out that Eq.(1)has periodic wave solutions and asymptotic behaviors,which can be used to describe certain situations from the fluid mechanics,ocean dynamics and plasma physics.Recently,Man and Lou put forward a new way of thinking to get the lump and lumpoff solutions of the NLEEs in Ref.[29].This result is very helpful for us to study some physical phenomena in engineering.The main aim of this paper is to investigate the lumps,lumpoffand the rogue waves with predictability of the gKDKK equation.

The rest of this paper is structured as follows.In Sec.2,the general lump solutions for(2+1)-dimensional gKDKK equation are obtained with the help of the dependent variable transformation u=12h1h?12(lnf)xxand the moving path of the lump waves is also described.In Sec.3,we discussed the lumpoffwaves based on the assumed equation Eq.(23).In Sec.4,the special rogue waves of the Eq.(1)and the time and place of its occurrence are provided.Finally,conclusions and discussions are provided in Sec.5.

2 General Lump Solutions for gKDKK Equation

In the present paper we consider a variable transformation

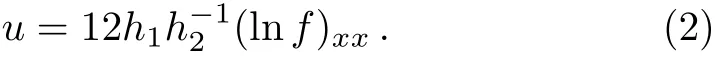
Substitution of Eq.(2)into Eq.(1),the Hirota bilinear form for the gKDKK equation can be expressed as[25]

Based on the results provided in Refs.[10,29–30],we can assume that f is a general quadratic function reads

with

in which A ∈ R4×4is a symmetric matrix,f0is a positive constant.In particular,putting x0=1,x1=x,x2=y,and x3=t,then f can be written as follows

From the properties of logarithmic function,it is easy to find that f must be positive.Therefore,we suppose that aijcan be represented as

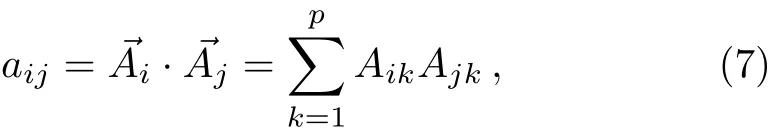
where

are p dimension vectors and lk,mk,nk,χkare real constants to be determined later.Moreover,if takeone can get

Thus f is always positive with aijdefined by Eq.(7).Substituting Eq.(6)into Eq.(3)and collecting all the coefficients of the same exponent of x,y,t,we can get a set of algebraic equations.By solving these objective equations,we find that these equations need only fi ve solutions as follows where a00,a01,a02,a11,a12,and a22are all arbitrary constants.Furthermore,inserting Eqs.(6)–(8)into the bilinear form Eq.(3),we can also find the following relationships

It means that these objective equations need only two constraint conditions under the constraint of Eqs.(10)and(11).

Then,according to the results in Ref.[29],taking p=3 forAi,the lump solutions of Eq.(1)will be more generalized than other values of p.That being said,the two constraint conditions can be written as

where lk,mk,χk(k=1,2,3)are all arbitrary parameters,and

By applying the transformation u=12h1h?12(lnf)xx,the general lump solution of the(2+1)-dimensional gKDKK equation has the following forms

in which

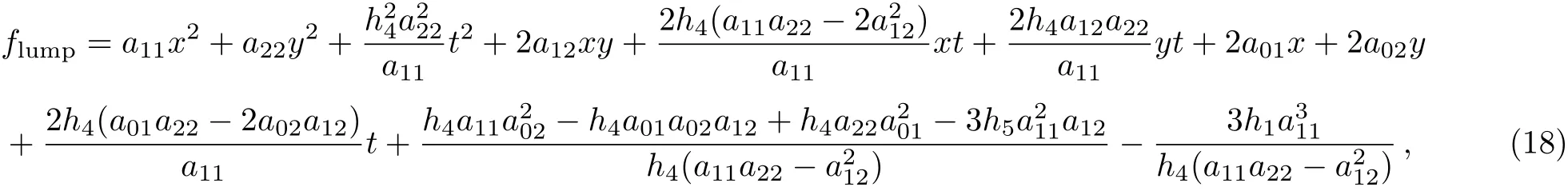
where aijconsists of lk,mk,nk,χkin Eq.(7)with Eq.(8),and nkis defined by lkand mk.

Especially,if we can find the critical point of the lump waves,the moving path of the lump waves can be described.Consider the case of fx=fy=0,we have

That is to say,the lump wave move along the straight line

The graphical representation of lump solution Eq.(17)is described in Fig.1 with the following special parameters:

Moreover,the moving path of lump waves is given by calculating the expression Eq.(19),one has

This observation can be clearly seen in Fig.1,the lump wave has the localized characteristic when t=0,and will propagate along a straight line as time changes.

Fig.1(Color online)Space diagrams(a)–(c)and density plots(d)–(f)of lump solution Eq.(17)for Eq.(1)with the parameters Eq.(21).(a),(d)t=?8;(b),(e)t=0;(c),(f)t=8.

3 lumpoff solutions for gKDKK Equation

The so-called lumpoff solution is the interaction between lump wave solutions and stripe soliton wave solutions.At one point in time,the two are separated from each other and exist alone.But as time goes on,the lump waves will be swallowed by the solitary soliton waves.Before the beginning of the structural lump solutions,we assume flumpoffcan be expressed as

where flumpis derived in Eq.(18),and k,l0,m0,n0,χ0are undetermined.The lump solutions and exponential solutions constitute the lumpoffwaves.It is not hard to find that the exponentiation part is dominant when

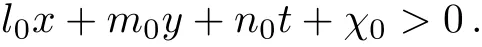
Otherwise,the lump solution only appears(that is l0x+m0y+n0t+χ0<0).

Substituting Eq.(23)into Eq.(1),we get

where a11,a12,a22are defined by Eq.(7)with Eq.(8),and k,χ0are free constants.The above results make us understand that l0and m0are completely determined by Eqs.(24)–(25).However,the n0is related to l0and m0.So what does that tell us the soliton waves are produced by lump waves.The existence of such lump waves in the soliton wave also exists.

Based on the condition above,substituting the flumpoffinto Eq.(2),the lumpoff solutions can be written as

where l0,m0,n0are given by Eqs.(24)–(26),and k,χ0are arbitrary constants.

Fig.2 (Color online)Space diagrams(a)–(c)and density plots(d)–(f)of lumpoffwaves Eq.(27)for Eq.(1)with the parameters Eq.(28).(a),(d)t=?2;(b),(e)t=4;(c),(f)t=12.

The corresponding dynamic characteristics of the lumpoffwaves are plotted in Fig.2 with the following special parameters:

Observation Eq.(23)is easy to find that the generation of lumpoffwaves is based on the premise that the lump part is unchanged.The moving path of lumpoff solution is given by calculating the expression Eq.(19)and has the following forms

Figure 2 shows the process of evolution for different selections of parameter.Obviously,the lump wave is cut by the soliton.We also notice that the lump waves appear when l0x+m0y+n0t+χ0<0 and covered by soliton in the end.

4 Rogue Waves with Predictability for gKDKK Equation

In the section,the special rogue wave solutions of Eq.(1)are considered.Its particularity lies in that the arising time and space can be predicted.In fact,the lump waves can be regarded as a special rogue waves.Next,we construct the rogue wave solutions for the gKDKK equation as follows

where flumpis shown in Eq.(18),and the specific expression of l0,m0,n0are provided by Eqs.(24)–(26),μ and λ0being two arbitrary constants to be determined.

By observing Eq.(30),it is easy to find that the rogue wave frogueis composed of two parts of lump wave and exponential part.In Eq.(30),the cosh part is obviously dominant.In other words,if and only if the following conditions are satisfied

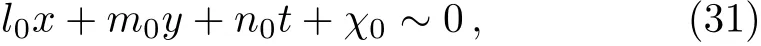
the lump wave is emerge.That is to say,only soliton wave appears and lump wave will appear.Substituting Eq.(30)into Eq.(3)and collecting all relevant coefficients of x,y,t,cosh,sinh,a series of equations have been obtained.Based on the previous computational results,we have

where a11,a12,a22are given by Eq.(7)with Eq.(8),andμis a free constant.

Via expressions(2),the rogue solution of gKDKK equation can be written as

where l0,m0,n0are defined by Eqs.(24)–(26),and a01,a11,a12,a13are defined by Eqs.(7)–(8). μ and χ0are all free constants.

In addition,we can see clearly from our results that the path and the emerge time of the rouge wave may be predict.Because the rogue wave will disappear with the loss of dominance,and it will appear only when l0x+m0y+n0t+χ0～0.Therefore,on the basis of the moving path of lump waves Eq.(17),we can predict the appearance time and place of the special rogue waves by utilizing the center line l0x+m0y+n0t+χ0=0 of a pair of resonance stripe soliton waves.The time t reads

and the place x,y read

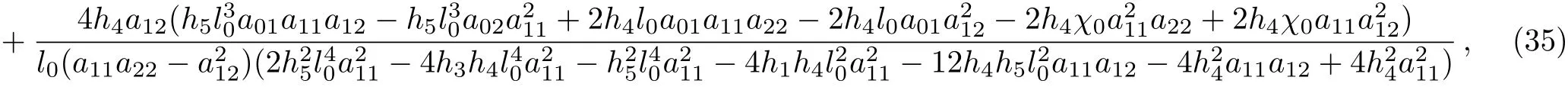
where χ0is free parameter,and l0is given in Eq.(24).

In order to analyze the propagation characteristics of the rogue wave in detail,we choose the following appropriate parameters to plot Fig.3:

Figure 3 describes the rogue wave will appear when t is at a special value.But with the change of time t,the rogue waves will eventually be covered by the solitary waves.

Fig.3 (Color online)Space diagrams(a)–(c)and density plots(d)–(f)of rogue waves Eq.(33)for Eq.(1)with the parameters Eq.(36).(a),(d)t=?1;(b),(e)t=0;(c)(f)t=1.

5 Conclusions and Discussions

In this paper,we mainly investigated the lump waves,lumpoffand rogue waves of the(2+1)-dimensional generalized Konopelchenko-Dubrovsky-Kaup-Kupershmidt equation. First,by constructing the special quadratic function Eq.(6)with a symmetric matrix,we have obtained the general lump solutions based on transform Eq.(2).It is worth emphasizing that the moving path of the lump waves Eq.(15)are given.Second,with the help of the ansatz Eq.(23),the lumpoff solution is also considered.Besides,the soliton is induced by the lumps,and so we say that the existence of the lump waves determines the existence of soliton.Furthermore,the rogue waves with predictability are derived when double solitons are induced by the lumps,we display the appearance time and place of the special rogue waves in Eqs.(34)–(35).Finally,the dynamic properties of these solutions are discussed by some 3-dimensional plots and contour plots with choices some special parameters.The lump waves and lumpoff are expected to play an increasingly important role in mathematical physics and engineering.