一類帶Hardy-Sobolev臨界指數(shù)的非局部問題正解的存在性

王躍,葉紅艷,索洪敏

(貴州民族大學(xué)數(shù)據(jù)科學(xué)與信息工程學(xué)院,貴州 貴陽550025)

1.引言和主要結(jié)果

本文研究如下一類帶Hardy-Sobolev 臨界指數(shù)的非局部問題

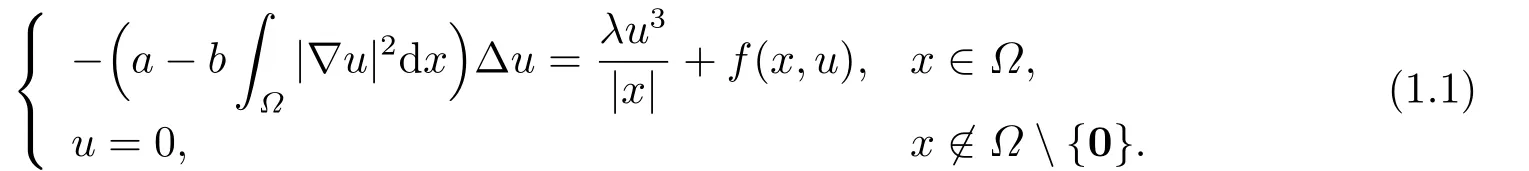
其中?是R3中的光滑有界域,常數(shù)a,b>0,參數(shù)λ>0,f(x,u) 是?×R 到R 的連續(xù)函數(shù).

含Hardy-Sobolev 臨界指數(shù)的問題在國內(nèi)外已有大量的研究成果.例如,問題

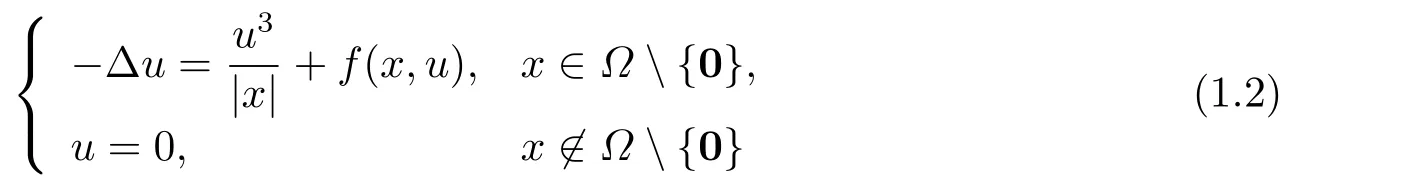
正解的存在性在[1-3]等文獻(xiàn)中都有研究,?通常是RN中的光滑有界域或等于RN(N是正整數(shù)).當(dāng)取a=λ=1,b=0時(shí),問題(1.2)便成問題(1.1)的一種特殊情形,因此問題(1.1)在理論上具有一定的研究意義.更多帶有Hardy-Sobolev臨界指數(shù)時(shí)正解的存在性及多重性問題的最新研究還可以從文[4-6]及其引用文獻(xiàn)中找到.另一方面,問題

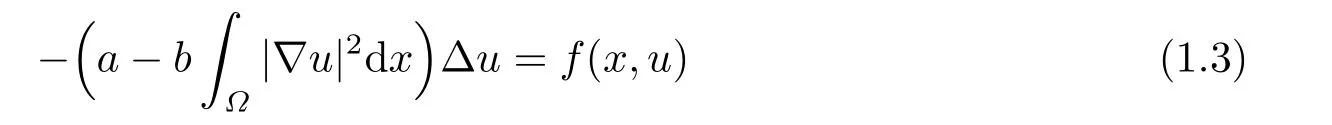
仍然含有非局部項(xiàng).通過文獻(xiàn)檢索,Dirichlet 邊界條件下問題(1.3) 的研究近年來很受關(guān)注.如文[7]通過變分方法和山路引理獲得f(x,u) =|u|p?2u時(shí)非平凡非正解和非平凡非負(fù)解的存在性,其中? ?RN是光滑有界域,N ≥3 時(shí)N= 1,2時(shí)2?= +∞;文[8]考慮了f(x,u) =fλ(x)|u|p?2u時(shí)解的多重性,其中? ?RN(N ≥3) 是光滑有界域,文中獲得fλ(x)∈L∞且1

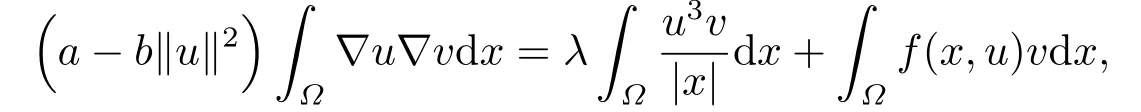
則把u定義為問題(1.1)的弱解(簡稱解),其中? ?u?vdx=?u,v?表示H10(?) 上的內(nèi)積,本文的主要結(jié)果如下:

定理1假設(shè)a,b,λ>0 且f(x,u) 滿足如下條件:

(f1)如果f(x,u)≥0且存在s<5使對x ∈?一致成立;

(f2)存在μ>4使|u|>0時(shí)對x ∈?有那么,問題(1.1)至少有一個(gè)正解.

2.預(yù)備知識

考慮泛函

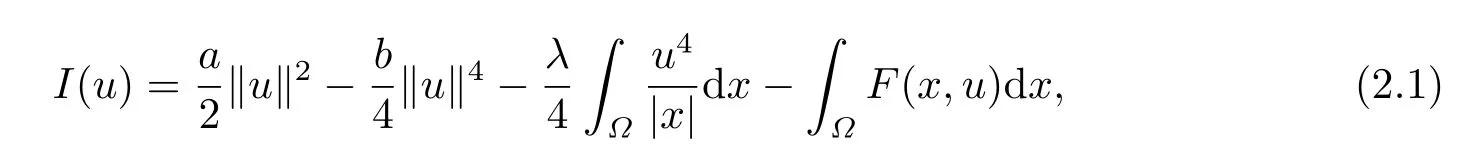
則對任意的v ∈H10(?) 有

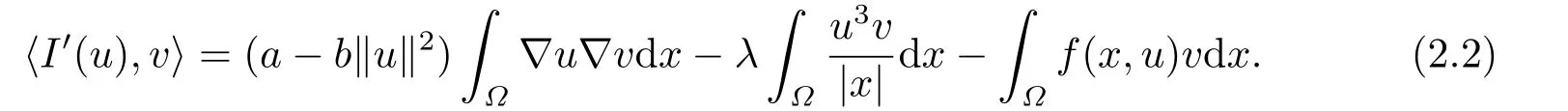
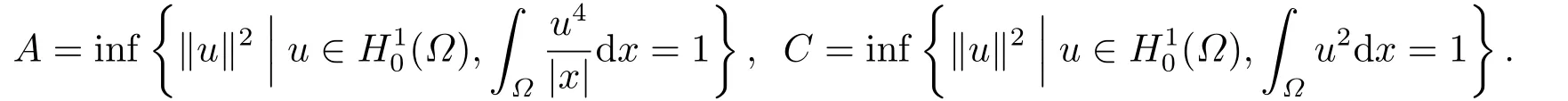
根據(jù)文[3]中定理3.1可知?= R3時(shí)A可取到.通過截?cái)嗉记芍苯佑?jì)算可得,對任意的正實(shí)數(shù)ε都存在對應(yīng)的函數(shù)及正常數(shù)C1,C2,C3滿足

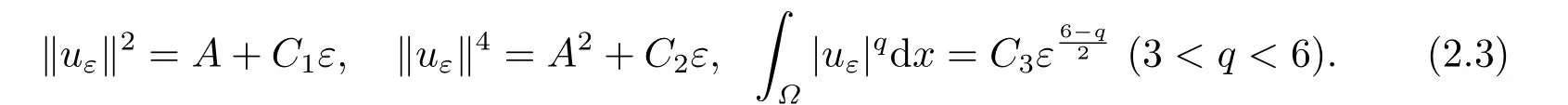
引理2.1若a,b,λ>0,(f1)和(f2)成立,那么對任意I滿足(PS)c條件.

證設(shè){un}是I的(PS)c序列,則有

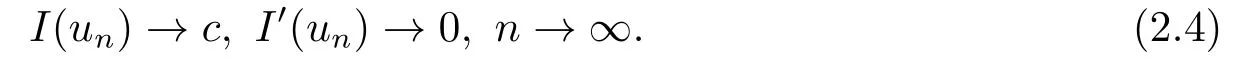
再由條件(f2)有

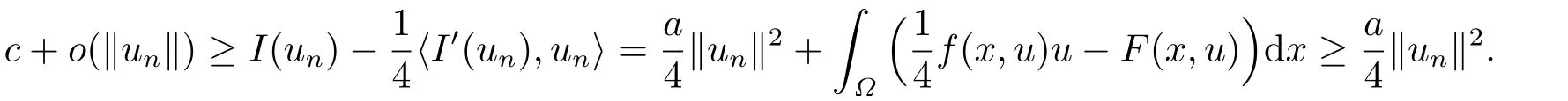
因此由Sobolev嵌入不等式可知{un}有界,從而存在u ∈H10(?) 及{un}的子列(不妨仍記為{un})使得n →∞時(shí): 在H10(?)中un ?u;在Lp(?)(1≤p <6)中un →u;對任意x ∈?,幾乎處處有un(x)→u(x).由(f1),對任意ε>0,存在常數(shù)mε,M >0,sε >s+1 使得

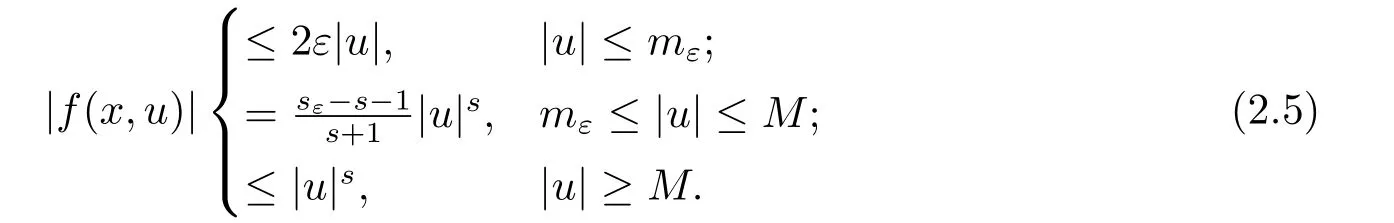
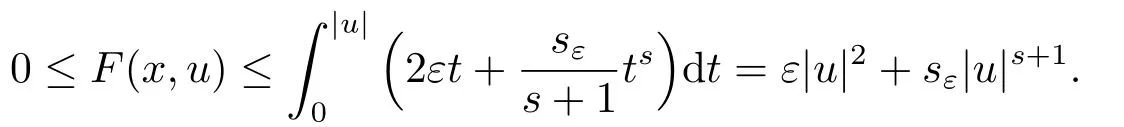
根據(jù)un ?u和Lebesgue 控制收斂定理(文[13]第27頁),對任意ε>0 都有

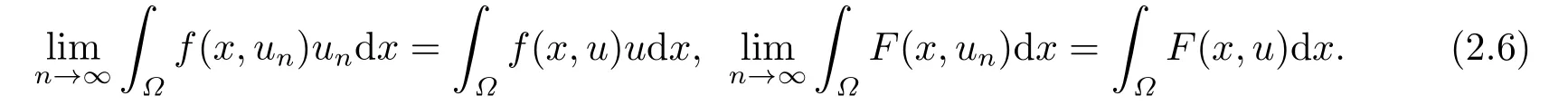
設(shè)ωn:=un ?u,則n →∞時(shí)‖ωn‖→0.若不然,總可以假設(shè)存在一個(gè){ωn}的子列(不妨仍記為{ωn}) 使得并且

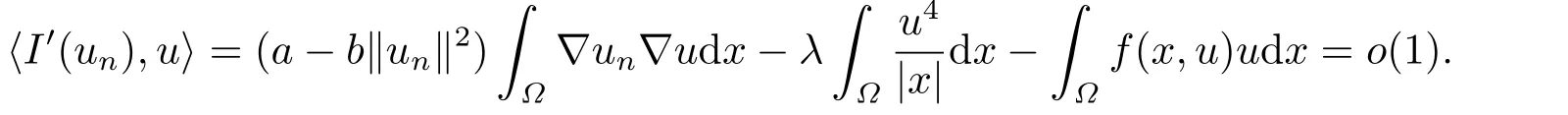
由Br′ezis-Leib引理(文[14]定理1) 和文[3]的引理4.3可知

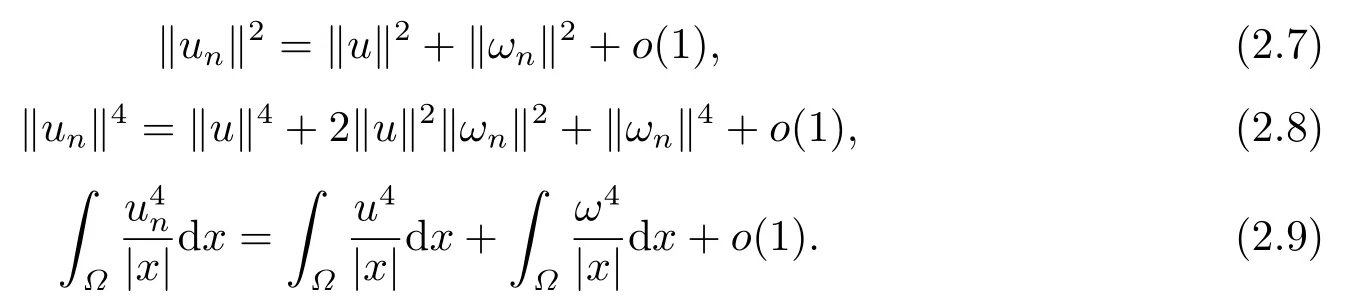
根據(jù)(2.4)-(2.9)式可得

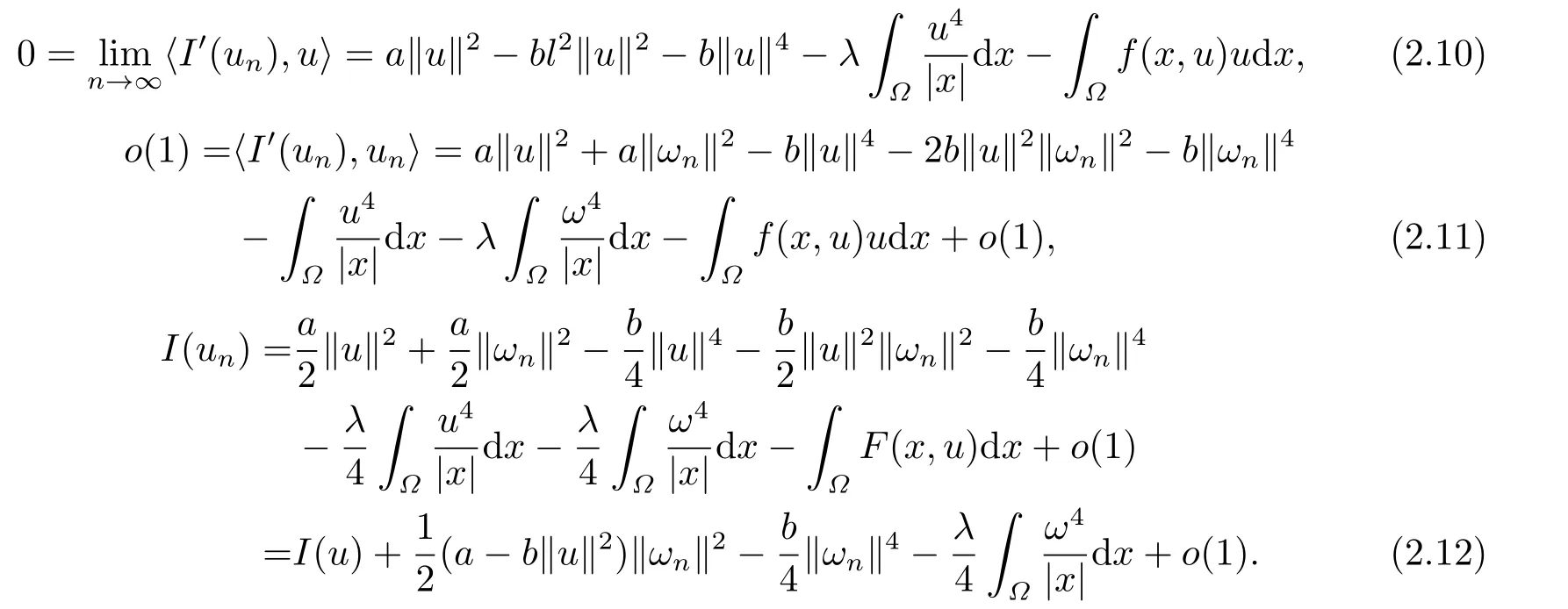
再由(2.10)-(2.11)式,Hardy-Sobolev 嵌入不等式及(f2) 可得

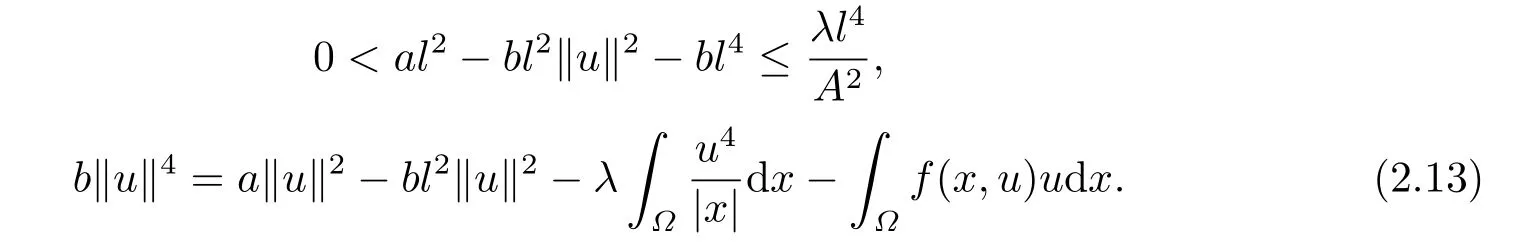
因此

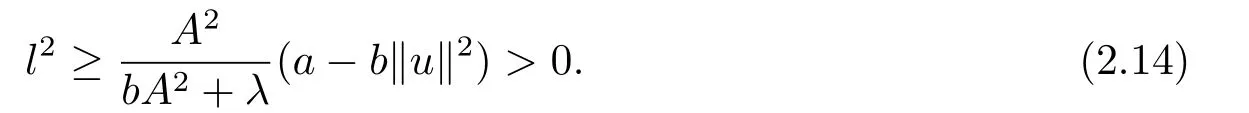
根據(jù)條件(f2),可取ε >0 較小使得當(dāng)|u| ≤ε時(shí)當(dāng)|u|>ε時(shí)f(x,u)u ?4F(x,u)>0,從而將(2.13)式代入泛函(2.1)得

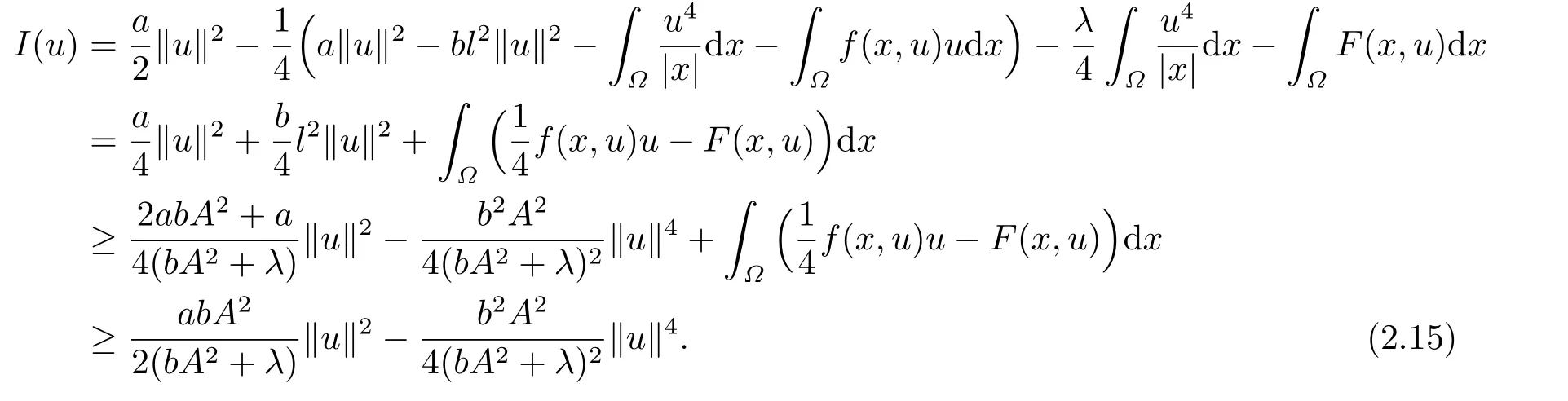
另外,從(2.12)-(2.14)式和Hardy-Sobolev嵌入不等式可得出

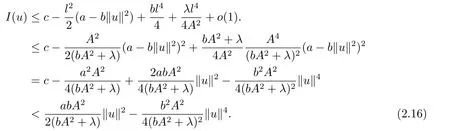
引理2.2如果a,b,λ>0,(f1) 和(f2) 成立,則存在常數(shù)ε0>0,對任意的ε ∈(0,ε0) 及t ∈R 總有

證顯然成立.當(dāng)|u|>0 且|t|>0 時(shí)由條件(f2) 可知,存在正常數(shù)C4使得F(x,u)≥C4|u|μ,再根據(jù)(2.3),存在正常數(shù)C5,C6使得

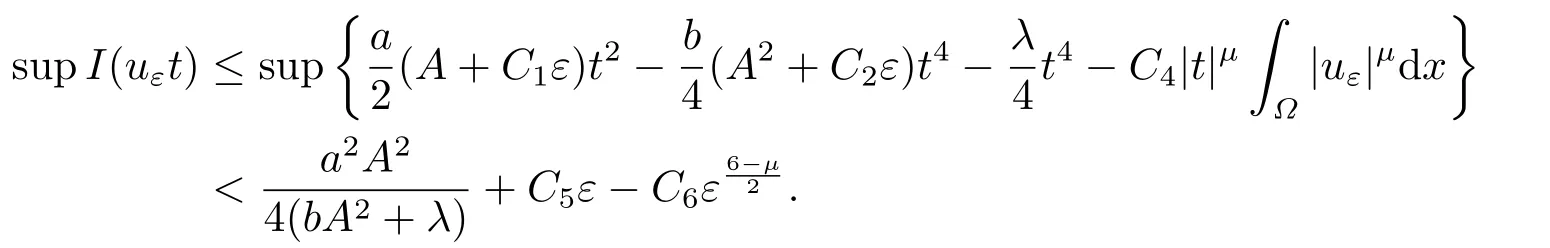
根據(jù)條件(f2)可知μ>4,故存在對任給的ε ∈(0,ε0),總有從而

3.定理1的證明

由(f1),當(dāng)|t|較小時(shí)有從而存在時(shí)有

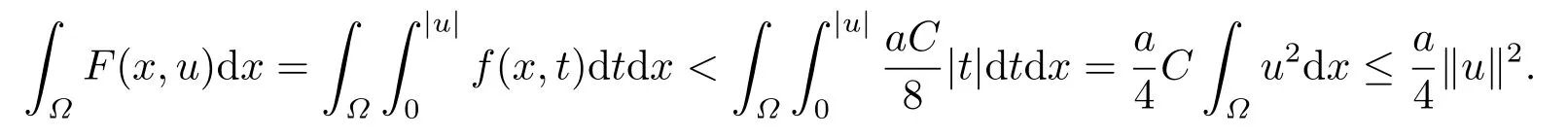
此時(shí)

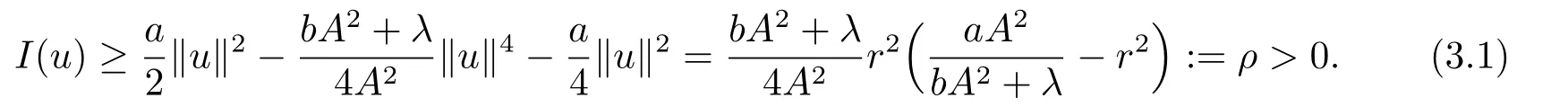
由(f2)有而故存在e ∈H10(?)滿足使得

從而泛函I滿足山路結(jié)構(gòu).設(shè)

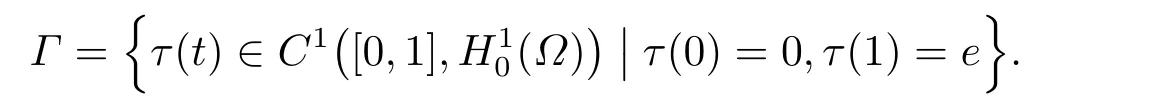
由(3.1)和(3.2)可知I(τ(0))=0,I(τ(1))≤0.而(2.1)-(2.2)表明I(τ(t))∈C1([0,1],H10(?)),從而因此通過引理2.2可得

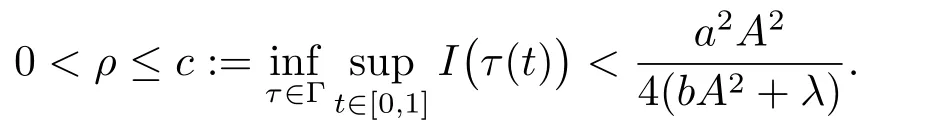
根據(jù)山路引理(文[15]定理2.1,定理2.4),存在{un}?H10(?)使得n →∞時(shí)I(un)→c,I′(un)→0.再由引理2.1可知I滿足(PS)c條件,因此c是I的一個(gè)臨界值.即存在u ∈H10(?)使得I(u) =c>0,I′(u)=0.從而u是問題(1.1)的一個(gè)非平凡解.此時(shí)在(2.2)中取v=u有0,而根據(jù)條件(f1)可得f(x,u)≥0,因此再根據(jù)極大值原理可得出u可以為正解.定理證畢.