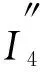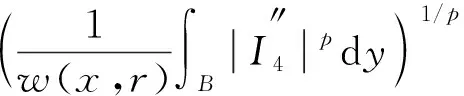廣義Morrey空間上H?rmander象征的 雙線性擬微分算子的交換子
陶雙平, 李巧霞
(西北師范大學 數(shù)學與統(tǒng)計學院, 蘭州 730070)
1 引言與主要結果
設T是雙線性算子,a(x)是n上的函數(shù), 雙線性交換子定義為
[T,a]1(f,g)=T(af,g)-aT(f,g), [T,a]2(f,g)=T(f,ag)-aT(f,g).
當T是單線性擬微分算子時, Calderón[1]證明了核為(-n-1)階齊次時,T與Lipschitz函數(shù)生成的交換子在Lebesgue空間上是有界的, 即
‖[T,a](f)‖Lp‖a‖Lip1‖f‖Lp, 1 (1) 設ρ,δ≥0,m∈, 如果(x,ξ)∈2n且對所有多重指標α,β, 都成立(1+|ξ|)m+δ|α|-ρ|β|, 則稱象征σ(x,ξ)屬于H?設相應的線性擬微分算子定義為 定義1[17]設w:n×(0,+∞)→(0,+∞), 1≤p<∞, 廣義Morrey空間Lp,w(n)定義為 其中B(x,r)表示以x為心、r為半徑的開球. 易見, 當w(x,r)=rλ,λ∈(0,n)時,Lp,w(n)即為經(jīng)典的Morrey空間Lp,λ(n). 文獻[18-19]進一步完善了Morrey空間的相關結果. 定義2[20]設b∈Lloc(n), 如果則稱b∈BMO(n). 其中: 本文主要結果如下: 取w(x,r)=rλ(0<λ 推論1在定理1的條件下, 交換子[Tσ,a]j(j=1,2)從Lp1,λ(n)×Lp2,λ(n)到Lp,λ(n)是有界的. 推論2在定理2的條件下, 交換子[[Tσ,a]j,b]i(i,j=1,2)是從Lp1,λ(n)×Lp2,λ(n)到Lp,λ(n)上的有界算子. 記AB表示A≤CB, 其中C是不依賴于主要函數(shù)或參量的常數(shù), 在不同之處可取不同的值.E?n, 用χE表示集合E的特征函數(shù). 1≤p≤∞,p′表示p的對偶指標, 即1/p+1/p′=1. K(x,y,z)=?eiξ·(x-y)eiη·(x-z)σ(x,ξ,η)dξdη, K1(x,y,z)=(a(y)-a(x))K(x,y,z),K2(x,y,z)=(a(z)-a(x))K(x,y,z). 引理1[6]當x≠y或x≠z時, 成立 |Kj(x,y,z)|‖a‖Lip1(|x-y|+|x-z|+|y-z|)-2n, 對交換子[Tσ,a]j(j=1,2)做如下分解: 由引理2, 有 下面估計I2. 設x∈B,y∈(2B)c,z∈2B, 注意到 |x-y|+|x-z|+|y-z|~|x-y|+|x-z|≥|x-y|, 由引理1和引理2及H?lder不等式, 有 因此 對于I3, 類似于I2的估計, 易得 最后估計I4. 設x∈B,y∈(2B)c,z∈(2B)c, 注意到 |x-y|+|x-z|+|y-z|~|x-y|~|x-z|, (2) 由引理1和H?lder不等式, 得 因此 綜合上述估計, 可得‖[Tσ,a]j‖Lp,w‖a‖Lip1‖f‖Lp1,w1‖g‖Lp2,w2(j=1,2). 定理1證畢. 引理3[20]若b∈BMO(n), 則對0 類似定理1的證明, 有 這里只證明i=1的情形,i=2的情形類似. 對I1, 由引理2有 下面估計I2. 將I2分解為 I2, 設x∈B,y∈(2B)c,z∈2B, 注意到|x-y|+|x-z|+|y-z|~|x-y|, 由引理1和H?lder不等式得 從而由引理3, 有 同理, 有 因此, 于是得I2的估計: 與I2的估計方法類似可得I3的估計: 最后估計I4. 將I4分解為 I4. 設x∈B,y∈(2B)c,z∈(2B)c, 注意到式(2), 應用H?lder不等式, 得 從而有 綜合上述估計, 有‖[[Tσ,a]j,b]1(f,g)‖Lp,w‖a‖Lip1‖b‖BMO‖f‖Lp1,w1‖g‖Lp2,w2. 定理2證畢.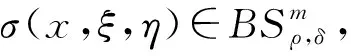
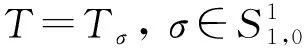
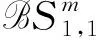
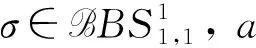
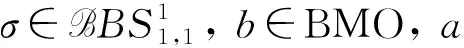
2 定理的證明
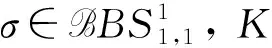
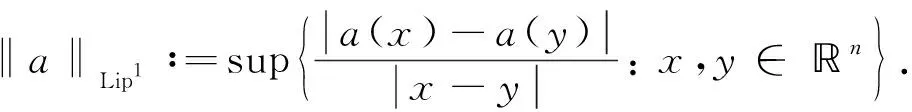
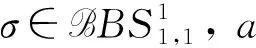
2.1 定理1的證明
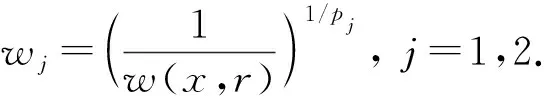
2.2 定理2的證明