分?jǐn)?shù)布朗運(yùn)動(dòng)下帶交易費(fèi)用和紅利的兩值期權(quán)定價(jià)

韋才敏,林先偉,范 衠

(1.汕頭大學(xué)數(shù)學(xué)系,廣東汕頭 515063)

(2.汕頭大學(xué)數(shù)字信號(hào)與圖像處理技術(shù)重點(diǎn)實(shí)驗(yàn)室,廣東汕頭 515063)

1 引言

期權(quán)定價(jià)的研究是數(shù)理金融的核心內(nèi)容之一.自從1973年著名的Black-Scholes模型和結(jié)果發(fā)表后,期權(quán)定價(jià)理論和應(yīng)用得到了迅速發(fā)展[1].但是經(jīng)典Black-Scholes模型過(guò)于理想化,與實(shí)際存在很大程度的摩擦.而分?jǐn)?shù)布朗運(yùn)動(dòng)具有金融市場(chǎng)所需要的長(zhǎng)時(shí)間相關(guān)性和自相似性等特征,其已經(jīng)成為描述標(biāo)的資產(chǎn)價(jià)格過(guò)程的一個(gè)有力工具.1989年P(guān)eter[2]提出了將資產(chǎn)價(jià)格的變化用分?jǐn)?shù)布朗運(yùn)動(dòng)來(lái)刻畫,并論證了資產(chǎn)價(jià)格服從幾何分?jǐn)?shù)布朗運(yùn)動(dòng)則其收益率服從分形分布;Ducan[3]研究了關(guān)于分?jǐn)?shù)布朗運(yùn)動(dòng)的隨機(jī)積分理論;Elliot和Hoke[4]研究了在Hurst指數(shù)在情況下的分?jǐn)?shù)布朗運(yùn)動(dòng),他們通過(guò)Wick積的方法得到了Girsanov定理和分?jǐn)?shù)It?o公式;Hu和?ksendal[5]通過(guò)Wick積分和分?jǐn)?shù)白噪聲分析進(jìn)一步發(fā)展了分?jǐn)?shù)布朗運(yùn)動(dòng)積分理論,證明了It?o型分?jǐn)?shù)Black-Scholes市場(chǎng)無(wú)套利且完備的;Christian和Bender[6]將其推廣到任意Hurset指數(shù).

交易成本對(duì)于期權(quán)定價(jià)來(lái)說(shuō)是一個(gè)重要的因素,許多學(xué)者對(duì)此做了很多研究.Leland[7]提出了將修正的波動(dòng)率應(yīng)用在解決有交易費(fèi)用的Black-Scholes模型的對(duì)沖誤差;Gaussion[8]證明了在分?jǐn)?shù)布朗運(yùn)動(dòng)下任何正的成比例交易成本大小能夠消除套利機(jī)會(huì).Zhang和Pan[9]給出了分?jǐn)?shù)布朗運(yùn)動(dòng)模型下帶交易費(fèi)用和紅利的亞式期權(quán)定價(jià)公式.Wang[10]解決了在分?jǐn)?shù)布朗運(yùn)動(dòng)下離散時(shí)間的含有交易費(fèi)用期權(quán)定價(jià)問(wèn)題.此外,隨著交易市場(chǎng)的不斷成熟,由標(biāo)準(zhǔn)的看漲期權(quán)和看跌期權(quán)衍生出的非標(biāo)準(zhǔn)化產(chǎn)品日益增多,這些產(chǎn)品稱之為新型期權(quán).兩值期權(quán)就是新型期權(quán)的一種.目前關(guān)于兩值期權(quán)的研究有:Thavaneswaran等人[11]用模糊理論研究?jī)芍灯跈?quán)的定價(jià)問(wèn)題;袁國(guó)軍[12]在半離散化CEV過(guò)程中得到兩值期權(quán)價(jià)格的差分格式;Hofer和Leitner[13]研究了兩值期權(quán)的相對(duì)定價(jià)問(wèn)題;吳云和何建敏[14]推導(dǎo)了兩值期權(quán)的解析解并闡述了二叉樹方法在兩值期權(quán)定價(jià)中的應(yīng)用;孫天宇[15]研究了標(biāo)準(zhǔn)布朗運(yùn)動(dòng)下帶交易費(fèi)用和紅利的兩值期權(quán)定價(jià)問(wèn)題.然而,在標(biāo)準(zhǔn)布朗運(yùn)動(dòng)下研究?jī)芍灯跈?quán)定價(jià),并不符合實(shí)際的金融市場(chǎng).

本文在上述研究的基礎(chǔ)上,將標(biāo)準(zhǔn)布朗運(yùn)動(dòng)下帶交易費(fèi)用和紅利的兩值期權(quán)定價(jià)問(wèn)題推廣到Hurst指數(shù)為的分?jǐn)?shù)布朗運(yùn)動(dòng)更一般的情況.假設(shè)標(biāo)的資產(chǎn)服從幾何分?jǐn)?shù)布朗運(yùn)動(dòng),通過(guò)無(wú)風(fēng)險(xiǎn)套利原則和分?jǐn)?shù)It?o公式建立了分?jǐn)?shù)布朗運(yùn)動(dòng)環(huán)境下兩值期權(quán)的定價(jià)模型.利用偏微分方程的相關(guān)知識(shí)求解此模型,得到了現(xiàn)金或無(wú)值看漲期權(quán)(CONC)和資產(chǎn)或無(wú)值看漲期權(quán)(AONC)的定價(jià)公式,并由此推出了現(xiàn)金或無(wú)值看跌期權(quán)(CONP)和資產(chǎn)或無(wú)值看跌期權(quán)(AONP)的定價(jià)公式.

2 基本模型

兩值期權(quán)(binary option)是合同條款變化產(chǎn)生的新型期權(quán),具有不連續(xù)收益的特點(diǎn)[16].一般分為兩種類型:

(1)現(xiàn)金或無(wú)值看漲期權(quán)(cash-or-nothing call)(簡(jiǎn)寫為CONC):在到期日,若股票價(jià)格低于執(zhí)行價(jià)格,則期權(quán)價(jià)值為零;若大于執(zhí)行價(jià)格,則按規(guī)定支付現(xiàn)金1元.

(2)資產(chǎn)或無(wú)值看漲期權(quán)(asset-or-nothing call)(簡(jiǎn)寫為AONC):在到期日,若股票價(jià)格低于執(zhí)行價(jià)格,則期權(quán)價(jià)值為零;若大于執(zhí)行價(jià)格,則按規(guī)定支付股價(jià).

引理1(分?jǐn)?shù)It?o公式[9])假設(shè)V=V(St,t)是一個(gè)關(guān)于St和t的二元函數(shù),隨機(jī)過(guò)程St滿足以下隨機(jī)微分方程

從而得到

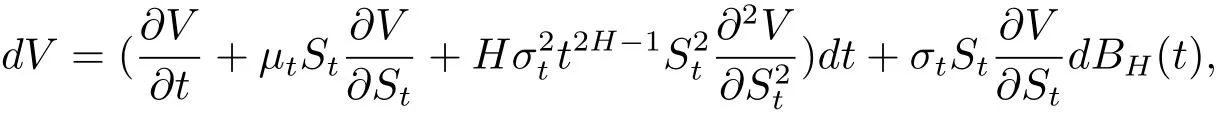
其中μt,σt分別表示漂移項(xiàng)和擴(kuò)散項(xiàng),BH(t)={BH(t),t≥0}是一個(gè)帶有Hurst指數(shù)H(0＜H＜1)的分?jǐn)?shù)布朗運(yùn)動(dòng).

定義1[10]假設(shè)(?,F,P)是一個(gè)完備的概率空間,Hurst指數(shù)為H(0＜H＜1)的分?jǐn)?shù)布朗運(yùn)動(dòng)BH(t)={BH(t),t≥0}是一個(gè)連續(xù)的高斯過(guò)程,且滿足

(1)BH(0)=E(BH(t))=0;

風(fēng)險(xiǎn)資產(chǎn)(如股票)價(jià)格St滿足下列隨機(jī)微分方程dSt=(μt?qt)Stdt+σtStdBH(t),其中μt,qt,σt分別表示預(yù)期收益率,紅利率和波動(dòng)率,BH(t)={BH(t),t≥0}是一個(gè)帶有Hurst指數(shù)H(0＜H＜1)的分?jǐn)?shù)布朗運(yùn)動(dòng).

考慮標(biāo)的資產(chǎn)支付紅利,紅利率為qt,到期日為時(shí)間T,敲定價(jià)格為K,作以下假設(shè)

(1)假設(shè)標(biāo)的資產(chǎn)(股票)價(jià)格St服從幾何分?jǐn)?shù)布朗運(yùn)動(dòng)

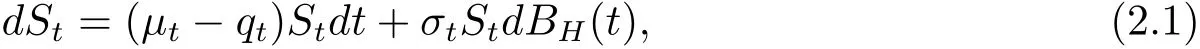
這里μt,qt,σt分別表示預(yù)期收益率,紅利率和波動(dòng)率,它們都是關(guān)于t的已知函數(shù),BH(t)={BH(t),t≥0}是一個(gè)帶有Hurst指數(shù)的分?jǐn)?shù)布朗運(yùn)動(dòng);

(2)沒有稅收,允許賣空;

(3)沒有無(wú)風(fēng)險(xiǎn)套利機(jī)會(huì);

(4)投資組合的預(yù)期收益率等于無(wú)風(fēng)險(xiǎn)利率;

(5)投資組合被每個(gè)δt修正,其中δt是有限的,固定的,小的時(shí)間間隔;

(6)有成比例交易成本.設(shè)k表示每單位股價(jià)的雙向交易成本.假設(shè)以價(jià)格St買入(νt＞0)或賣出(νt＜0)νt份股票,那么買入或賣出的交易成本為其中k 為常數(shù).

令V=V(St,t)表示CONC(或AONC)在時(shí)刻t的價(jià)格.構(gòu)造一個(gè)投資組合:一份CONC(或AONC)多頭,Δt份標(biāo)的資產(chǎn)空頭.在時(shí)刻t投資組合的價(jià)值為Πt=V?ΔtSt.應(yīng)用分?jǐn)?shù)It?o公式,在[t,t+δt]時(shí)間段內(nèi),

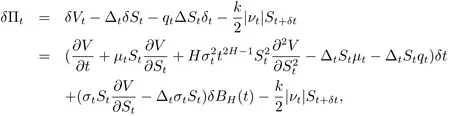
其中 νt= Δt+δt? Δt.

為了使投資組合Πt在[t,t+δt]無(wú)風(fēng)險(xiǎn),取,從而可得

其中

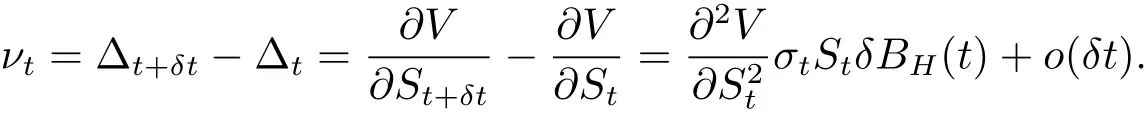
由于股票價(jià)格St滿足(2.1)式,則得

因此,可得交易費(fèi)用如下

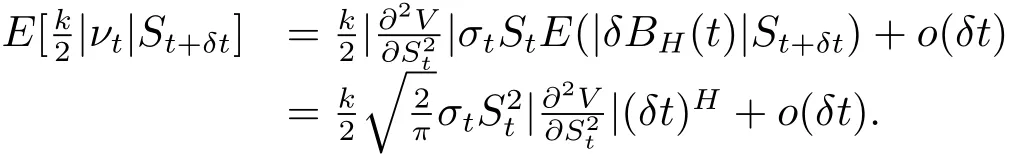
忽略高階項(xiàng)o(δt),有

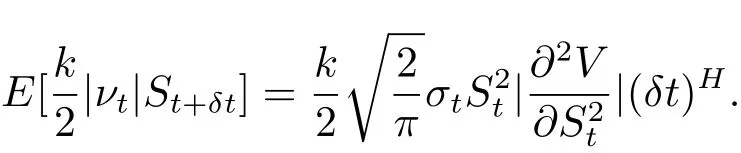
因此

由假設(shè)(4),得到

將(2.2)式代入(2.3)式,得到

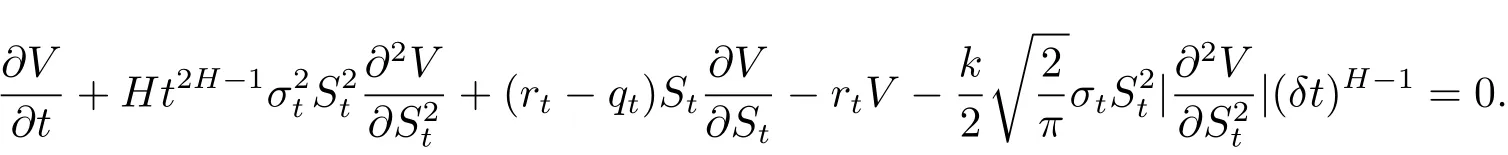
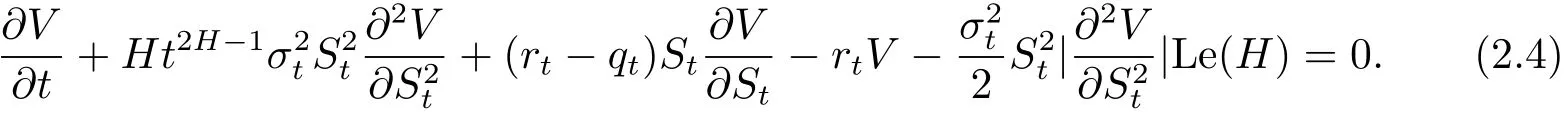
將(2.4)重寫如下

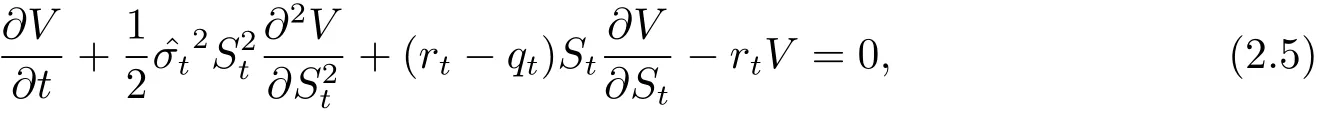
其中

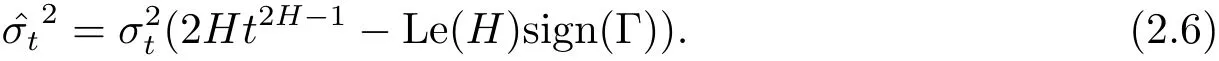
注1

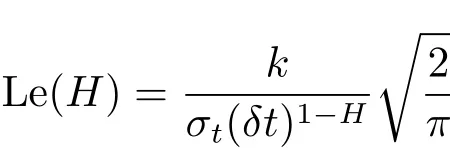
稱為分?jǐn)?shù)次Leland數(shù).

注2對(duì)于做空的單個(gè)歐式兩值期權(quán),也可以得到(2.5)式,若修正波動(dòng)率如下

注3對(duì)于做多的單個(gè)歐式兩值期權(quán),到期日的收益為(ST?K)+或(K?ST)+.由于它們是凸函數(shù),所以Γ＞0.然而,對(duì)于做空的單個(gè)歐式兩值期權(quán),到期日的收益為?(ST?K)+或?(K?ST)+.它們是凹函數(shù),所以Γ＜0.因此,對(duì)于單個(gè)的歐式兩值期權(quán),(2.6)和(2.7)式能夠做如下表示

從而得到在分?jǐn)?shù)布朗運(yùn)動(dòng)下帶交易費(fèi)用和紅利的兩值期權(quán)定價(jià)模型如下

這里H?(ξ)是 Heviside函數(shù).如果 ξ≥ 0,那么 H?(ξ)=1.否則,H?(ξ)=0.

3 兩值期權(quán)定價(jià)公式

3.1 現(xiàn)金或無(wú)值期權(quán)定價(jià)公式

定理1假設(shè)股票價(jià)格滿足(2.1)式,在時(shí)刻t帶有交易費(fèi)用和紅利的現(xiàn)金或無(wú)值看漲期權(quán)的定價(jià)公式為

證 由方程組(2.8)可以得到現(xiàn)金或無(wú)值看漲期權(quán)定價(jià)模型如下

因此,轉(zhuǎn)化為Cauchy問(wèn)題

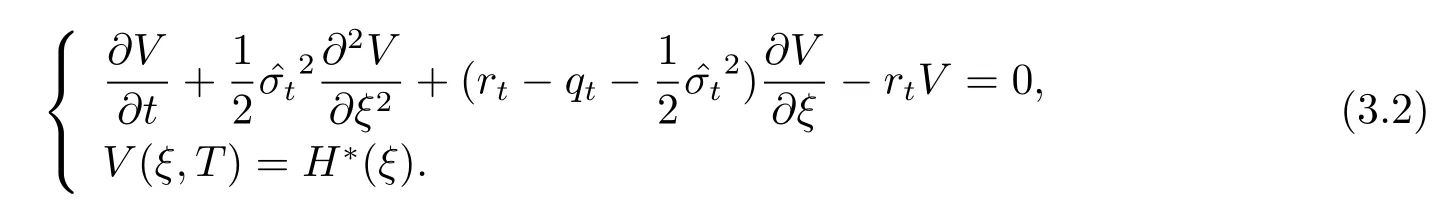
為求解Cauchy問(wèn)題,作函數(shù)變換W=V eβ(t),η=ξ+α(t),τ=γ(t),可得

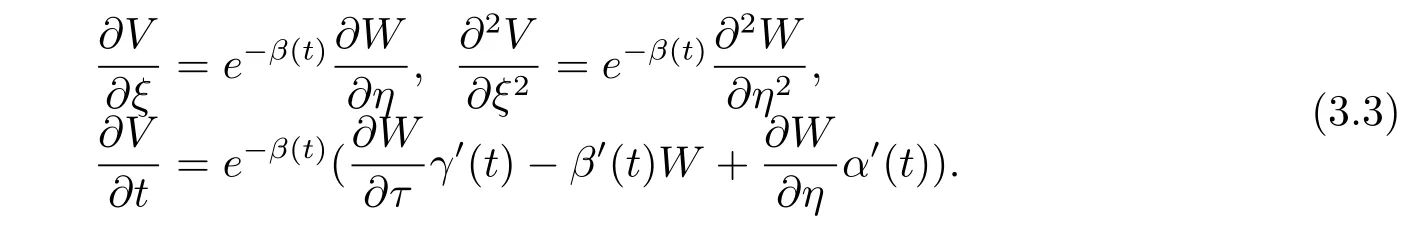
將式(3.3)代入上述方程(3.2),得到

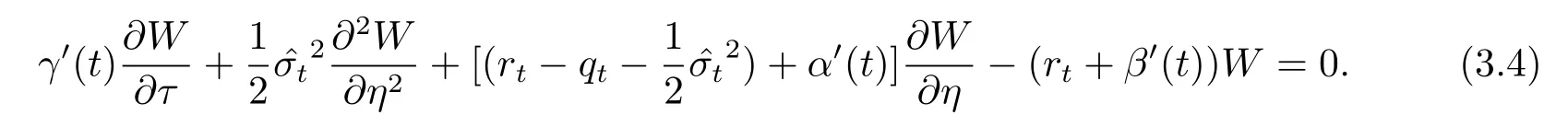
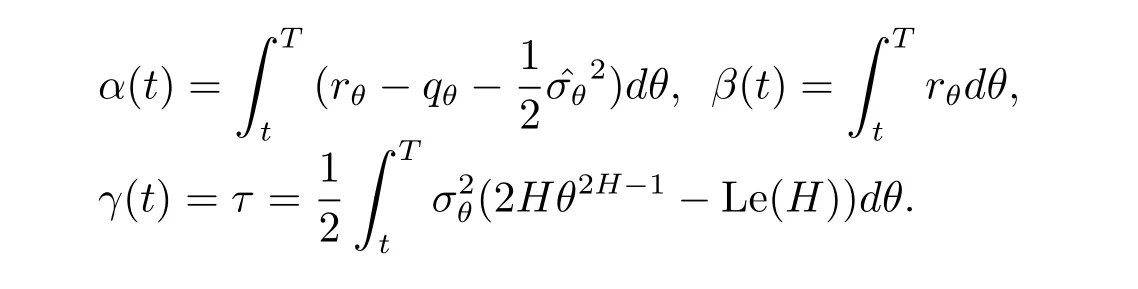
因此,方程組(3.2)轉(zhuǎn)化為如下行形式

方程組(3.5)的解可以用Possion公式如下表示

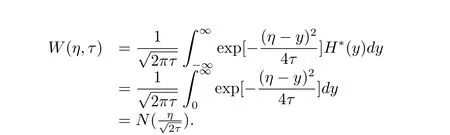
經(jīng)過(guò)變量代換,有

推論1 假設(shè)股票價(jià)格滿足(2.1)式,在時(shí)刻t帶有交易費(fèi)用和紅利的現(xiàn)金或無(wú)值看跌期權(quán)的定價(jià)公式為

3.2 資產(chǎn)或無(wú)值期權(quán)定價(jià)公式

定理2假設(shè)股票價(jià)格滿足(2.1)式,在時(shí)刻t帶有交易費(fèi)用和紅利的資產(chǎn)或無(wú)值看漲期權(quán)的定價(jià)公式為

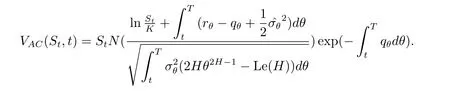
證 由方程組(2.8)可以得到資產(chǎn)或無(wú)值看漲期權(quán)定價(jià)模型如下

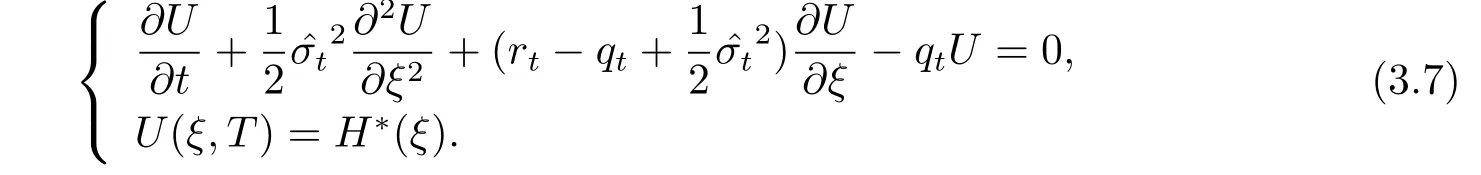
為求解Cauchy問(wèn)題,作函數(shù)變換W=Ueβ(t),η=ξ+α(t),τ=γ(t),可得

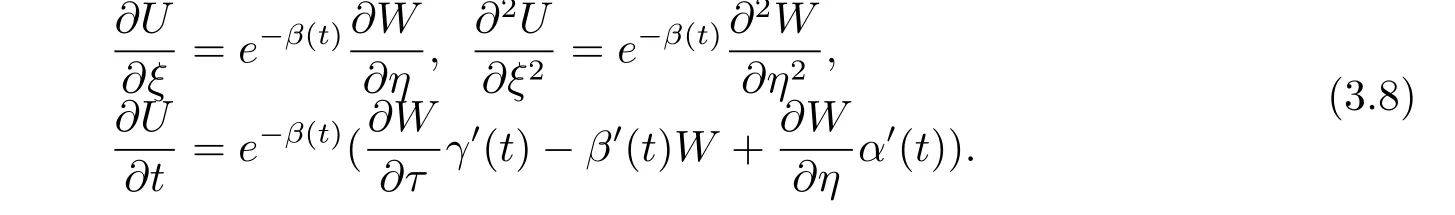
將式(3.8)代入(3.7)式,得到

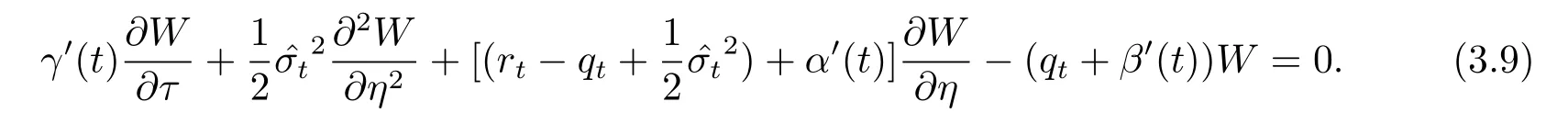
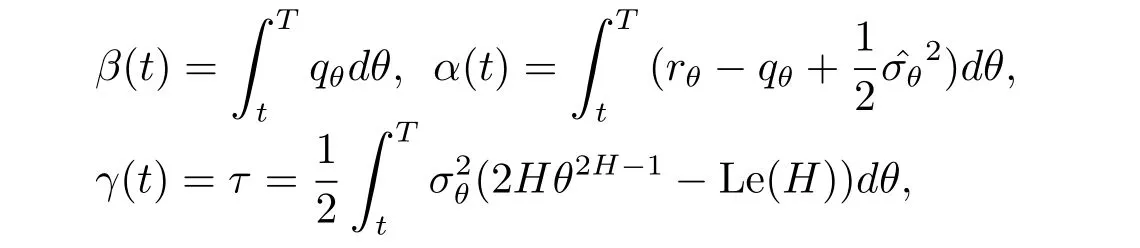
從而得到

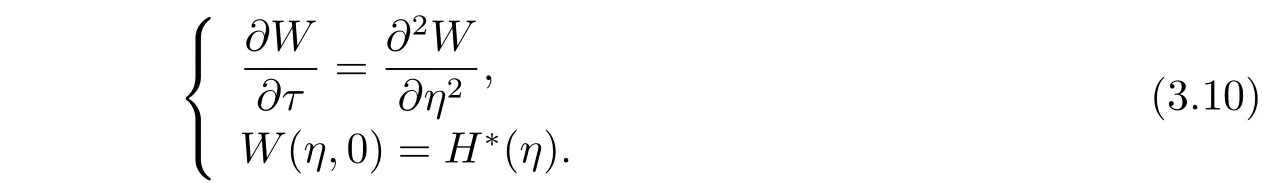
推論2 假設(shè)股票價(jià)格滿足(2.1)式,在時(shí)刻t帶有交易費(fèi)用和紅利的資產(chǎn)或無(wú)值看跌期權(quán)的定價(jià)公式為

注4對(duì)于單個(gè)歐式兩值期權(quán),如果做多頭,因?yàn)棣＃?,Leland數(shù)有可能大于2Ht2H?1,即當(dāng)

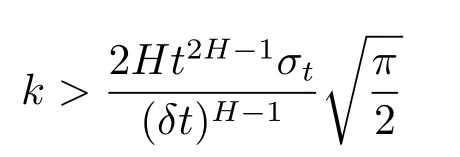
時(shí),方程(2.8)變成正向拋物型方程的終值問(wèn)題;因?yàn)檎驋佄镄头匠痰慕K值問(wèn)題是一個(gè)不適定問(wèn)題.所以為了使定解問(wèn)題(2.8)是適定問(wèn)題,必須要假定

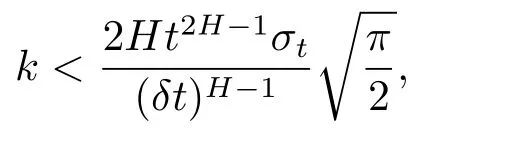
這表明交易費(fèi)用比較小,或者對(duì)沖風(fēng)險(xiǎn)的過(guò)程不能太頻繁,否則應(yīng)用Leland模型求解有交易費(fèi)用的期權(quán)價(jià)格是不正確的.

本文研究了在分?jǐn)?shù)布朗運(yùn)動(dòng)下帶交易費(fèi)用和紅利的兩值期權(quán)定價(jià)問(wèn)題,將標(biāo)準(zhǔn)布朗運(yùn)動(dòng)下的帶交易費(fèi)用的兩值期權(quán)定價(jià)問(wèn)題推廣到Hurst指數(shù)為分?jǐn)?shù)布朗運(yùn)動(dòng)的情況下.根據(jù)兩值期權(quán)的分類分為現(xiàn)金或無(wú)值期權(quán)和資產(chǎn)或無(wú)值期權(quán)兩種情況.通過(guò)利用無(wú)風(fēng)險(xiǎn)套利原則和分?jǐn)?shù)It?o公式,得到與之對(duì)應(yīng)的數(shù)學(xué)模型.求解此模型得到了現(xiàn)金或無(wú)值看漲期權(quán)和資產(chǎn)或無(wú)值看漲期權(quán)的定價(jià)公式,并在此基礎(chǔ)上得到了現(xiàn)金或無(wú)值看跌期權(quán)和資產(chǎn)或無(wú)值看跌期權(quán)的定價(jià)公式.在這個(gè)領(lǐng)域還有很多問(wèn)題去研究,比如在Levy過(guò)程,混合分?jǐn)?shù)布朗運(yùn)動(dòng)下討論此類問(wèn)題.