Double Wronskian Solutions for a Generalized Nonautonomous Nonlinear Equation in a Nonlinear Inhomogeneous Fiber?

Xi-Yang Xie(解西陽) and Gao-Qing Meng(蒙高慶)

Department of Mathematics and Physics,North China Electric Power University,Baoding 071003,China

AbstractA generalized nonautonomous nonlinear equation,which describes the ultrashort optical pulse propagating in a nonlinear inhomogeneous fiber,is investigated.N-soliton solutions for such an equation are constructed and verified with the Wronskian technique.Collisions among the three solitons are discussed and illustrated,and effects of the coefficients σ1(x,t),σ2(x,t),σ3(x,t)and v(x,t)on the collisions are graphically analyzed,where σ1(x,t),σ2(x,t),σ3(x,t)and v(x,t)are the first-,second-,third-order dispersion parameters and an inhomogeneous parameter related to the phase modulation and gain(loss),respectively.The head-on collisions among the three solitons are observed,where the collisions are elastc.When σ1(x,t)is chosen as the function of x,amplitudes of the solitons do not alter,but the speed of one of the solitons changes.σ2(x,t)is found to affect the amplitudes and speeds of the two of the solitons.It reveals that the collision features of the solitons alter with σ3(x,t)= ?1.8x.Additionally,traveling directions of the three solitons are observed to be parallel when we change the value of v(x,t).

Key words:inhomogeneous fiber,generalized nonautonomous nonlinear equation,bright N-soliton solution,double-Wronskian solution

1 Introduction

As the solution of the nonlinear evolution equations(NLEE),soliton has caused many interests,since it plays an important role in some fields of science and engineering such as the nonlinear optics,Bose-Einstein condensates, fluid mechanics and plasma physics.[1?5]Soliton is self-localized,robust,long-lived,and preserves the identity,when it travels in a nonlinear,dispersive medium.[6?7]

N-soliton solutions can be derived with the Hirota method and Darboux transformation,and they can be expressed as an N-th order polynomial in the N exponentials.[8?10]However,it is difficult to verify such N-soliton solutions,but the solutions in the Wronskian-form are relatively easier to be differentiate.[8?9,11]Therefore,the Wronskian solutions can be verified by virtue of the direct substitution into bilinear forms of the NLEE.[11?12]

It has developed the classical soliton concept for the nonlinear and dispersive systems that have been autonomous,which means that the time is the only factor that plays the role of the independent variable,and the solitary waves in nonautonomous nonlinear and dispersive systems can propagate in the form of nonautonomous solitons.[13?15]Under investigation in this paper is the following generalized nonautonomous nonlinear equation,[16?18]

which describes the ultrashort optical pulse propagating in the nonlinear inhomogeneous fiber,where t and x are the retarded time and normalized distance,respectively,ψ(x,t)is the complex envelope of the electrical field in a comoving frame,the coefficients σ1(x,t),σ2(x,t)and σ3(x,t)are the first-,second-and third-order dispersion parameters,respectively,ρ(x,t)is the Kerr nonlinear parameter,r(x,t)is the time-delaying effect parameter and v(x,t)is an inhomogeneous parameter related to the phase modulation and gain(loss).[16]Darboux transformation and soliton solutions for Eq.(1)have been investigated analytically.[16]Rogue-wave solutions for Eq.(1)have been derived via the generalized Darboux transformation.[17]Bright one-and two-soliton solutions for Eq.(1)have been studied.[18]

However,the N-soliton solutions for Eq.(1)with the Wronskian technique have not yet been reported yet,and the purpose of the present work will be to investigate the N-soliton solutions for Eq.(1).In Sec.2,we will derive the explicit N-soliton solutions for Eq.(1)in the form of the double-Wronskian determinant.In Sec.3,based on those solutions,the three-soliton solutions will be analyzed graphically.

2 Wronskian Form of theN-Soliton Solutions

Bilinear forms for Eq.(1)have been derived in Ref.[18]:

via the dependent variable transformation

under the constraints[16]

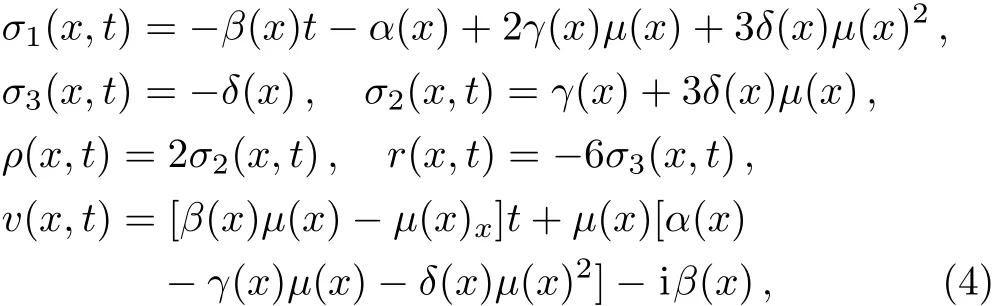
where g(x,t)is a complex function of x and t,and f(x,t)is a real one,while α(x),β(x),γ(x),μ(x),and δ(x)being the functions of x,Dxand Dtbeing the bilinear differential operators.[8]

The double-Wronskian determinant is defined as

with

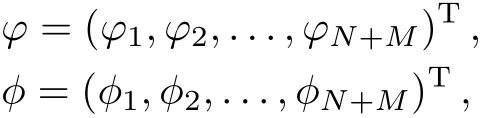
where φnand ?n(n=1,2,...,N+M)are all the complex functions of x and t,T represents the vector transpose,and N and M are both the integers.For convenience,WN,Mwill be written as

Considering the Lax pair of Eq.(1),we assume that

where

with

where ξjare all the complex constants.Then,we derive

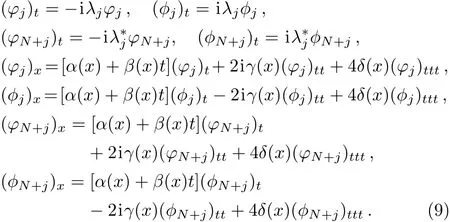
Based on the Wronskian technique,it can be proved that g and f defined in the double-Wronskian-form(6)indeed satisfy the Bilinear forms(2).Firstly,the derivatives of g and f with respect to x and t can be given as follows:

Based on the double-Wronskian determinant identities in the Appendix A,substituting the derivatives of g and f into the Bilinear forms(2),we derive

where the bold type denotes the contributions from the second half of the determinant.

Up to now,we have verified that g and f defined in the doubele-Wronskian-form(6)indeed satisfy the Bilinear forms(2).Therefore,N-soliton solutions for Eq.(1)can be expressed as

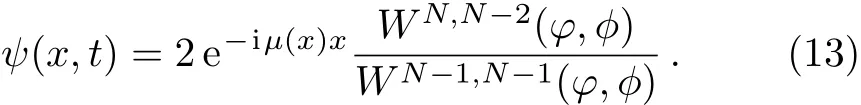
3 Discussions and Conclusion

For N=1,the bright one-soliton solution is given as

For N=2,the two-soliton solutions are shown as

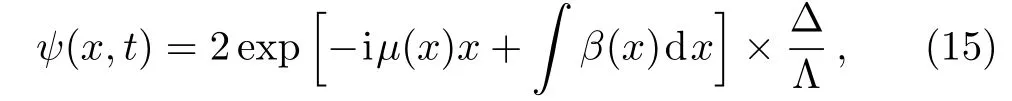
with

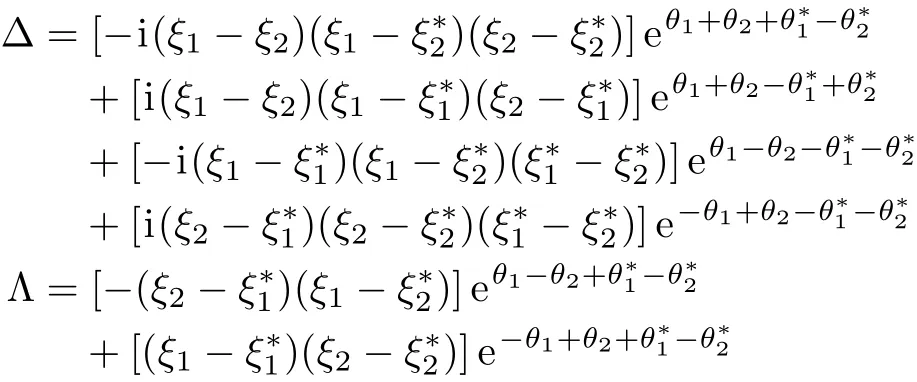
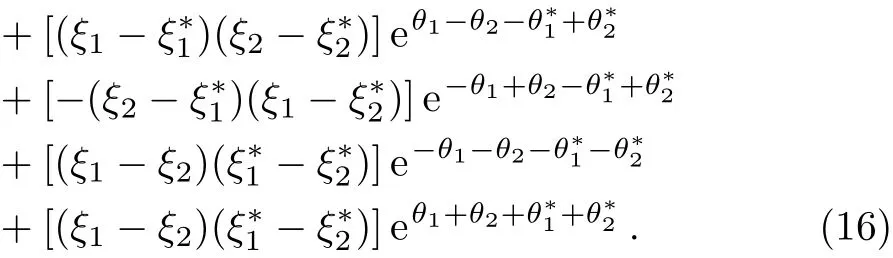
Similarly,we can obtain the expressions of the threeand four-soliton solutions,even the N-soliton solutions for Eq.(1).

Since the propagation of the one solitons and collisions between the two solitons have been investigated in Ref.[18],we will study the collisions among the three solitons in this section.Also,in fluences of σ1(x,t), σ2(x,t),σ3(x,t)and v(x,t)on the collisions are graphically discussed.

In Fig.1(a),we observe the head-on collision among the three solitons,where the solitons keep their shapes unchanged before and after the collision,which means the collision is elastc.When σ1(x,t)is chosen as the function of x,head-on collision also occurs in Fig.1(b),and amplitudes of the solitons do not alter,while the speed of one of the solitons changing,compared with Fig.1(a).In Fig.1(c),σ2(x,t)is found to affect the amplitudes and speeds of the two of the solitons.Figure 2(a)reveals that the collision features of the solitons alter with σ3(x,t)= ?1.8x.As shown in Fig.2(b),traveling directions of the three solitons are observed to be parallel.

In conclusion,a generalized nonautonomous nonlinear equation(i.e.,Eq.(1)),which describes the ultrashort optical pulse propagating in the nonlinear inhomogeneous fiber,has been investigated analytically in this paper.Via the Wronskian technique,the bright N-soliton solutions in the double-Wronskian-form for Eq.(1)have been constructed under the Constraints(4).In this paper,we have only studied the collisions among the three solitons,as the properties of the one and two solitons have been investigated.Also,in fluences of σ1(x,t), σ2(x,t), σ3(x,t)and v(x,t)on the collisions have been graphically analyzed.Our study may be helpful for investigating the soliton propagation and collision in the nonlinear inhomogeneous fiber theoretically and experimentally.Furthermore,higher-order effects such as the third-order dispersion and nonlinearity could lead to state transitions between breather and soliton,[19?21]which will be the focus of our future research.

Fig.1 (a)Collision among the three solitons via Solutions(13)with ξ1=1+0.9i, ξ2=1+i, ξ3=1+0.8i,σ1(x,t)=1,σ2(x,t)=1,σ3(x,t)=1 and v(x,t)=0;(b)The same as(a)except σ1(x,t)=7x;(c)The same as(a)except σ2(x,t)=x.

Fig.2 The same as Fig.1(a)except that(a)σ3(x,t)= ?1.8x;(b)v(x,t)= ?1.3i.

Appendix A

Some double-Wronskian determinant identities are given below:

Also,the following determinant identity is utilized:

where M is an N×(N?2)matrix with a,b,c and d denoting the N-dimensional column vectors.