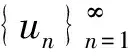右端項為L1時具退化強(qiáng)制橢圓方程弱解的存在性

李 仲 慶

(吉林師范大學(xué) 數(shù)學(xué)學(xué)院, 吉林 四平 136000)

1 引言與主要結(jié)果

假設(shè)條件：

(H1)a(x,s)是Ω×上的Carathéodory函數(shù), 滿足

(1)

其中0≤θ<1;

(H2)g(x,s,ξ)是Ω××N上的Carathéodory函數(shù), 滿足如下增長條件:

(2)

且

γ<α(1-θ);

(3)

(H3) 函數(shù)ρ(x),f(x)∈L1(Ω), 且存在Q>0, 使得對幾乎處處的x∈Ω, 有

|f(x)|≤Qρ(x).

(4)

考慮如下具退化強(qiáng)制的橢圓方程：

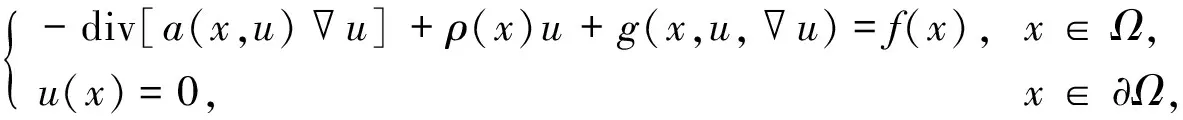
(5)

其中:Ω是N中具有光滑邊界?Ω的有界域; 假設(shè)條件(H1)～(H3)成立.

當(dāng)s→∞時,a(x,s)可能取0, 因此條件(H1)表明問題(5)是退化強(qiáng)制的, 故無法直接用經(jīng)典的一致型橢圓方程[1-2]的結(jié)論. 問題(5)的另一個特點是右端項f僅在L1中. 當(dāng)方程右端項的可積性較低時, 應(yīng)考慮Renormalized解或Entropy解[3-4], 因為可能不存在弱解. 下面以Laplace方程為例進(jìn)行說明. 考慮Laplace方程：

2 定理1的證明

下面分4步證明定理1.

1) 逼近方程.

首先給出問題(5)對應(yīng)的逼近方程:

(6)

其中: 截斷函數(shù)

Tk(s)=max{-k,min{k,s}}[7];

結(jié)合式(2)和式(9), 有

|gn(x,un,un)|≤n,

且

(10)

|fn(x)|≤Qρn(x).

(11)

2) 一致最大模估計.

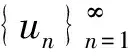
‖un‖L∞(Ω)≤C,

其中常數(shù)C僅依賴于θ,Q,γ,α,N,‖f‖L1(Ω), 但不依賴于n.

證明: 令

Gk(s)=s-Tk(s).

受文獻(xiàn)[6,9]的啟發(fā), 取GQ(H(un))作為問題(6)的一個檢驗函數(shù), 可得

① 根據(jù)式(1)對L1估計如下:

② 在集合{x∈Ω: |H(un)|>Q}上,un和GQ(H(un))的符號相同, 并由|H(s)|≤|s|, 有

(14)

④ 運(yùn)用式(11)可得

(16)

綜合①～④, 可得

(17)

式(17)及式(3)蘊(yùn)含: 對幾乎所有的x∈Ω和所有的n, 均有|H(un)|≤Q. 注意到

于是可得un是一致L∞有界的. 證畢.

3) 能量估計.

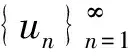
證明: 選取H(un)作為問題(6)的一個檢驗函數(shù), 可得

① 由式(1)和H(s)的表達(dá)式, 可得

② 因為s與H(s)的符號相同, 所以積分項I2非負(fù);

③ 對梯度項I3的估計如下:

④ 對右端項I4估計如下：

綜合①～④, 可得

利用un的L∞有界性可得

(18)

4) 極限過程.

引理3在假設(shè)條件(H1)～(H3)下, 在L2(Ω;N)中,u.

證明: 受文獻(xiàn)[6]啟發(fā), 選取

vn=(e2λ|un-u|-1)sign(un-u)

① 對A1做如下處理:

② 估計梯度項A2, 由式(10)可得

綜合①,②, 可得式(23)的估計為

根據(jù)Vitali定理[10], 式(24)右端4個積分項為n→∞時的無窮小量. 再由λ的定義, 可得

即在L2(Ω;N)中,u. 證畢.