Influence of Non-linear Radiation Heat Flux on Rotating Maxwell Fluid over a Deformable Surface:A Numerical Study
M.Mustafa,A.Mushtaq,T.Hayat,and A.Alsaedi
1School of Natural Sciences(SNS),National University of Sciences and Technology(NUST),Islamabad 44000,Pakistan
2Research Centre for Modeling and Simulation(RCMS),National University of Sciences and Technology(NUST),Islamabad 44000,Pakistan
3Department of Mathematics,Quaid-I-Azam University 45320,Islamabad 44000,Pakistan
4Department of Mathematics,Faculty of Science,King Abdulaziz University,P.O.Box 80257,Jeddah 21589,Saudi Arabia
1 Introduction
Fluid flow problems in rotating frame have been proven fascinating as well as challenging and these are met in numerous engineering applications such as rotor-stator systems,atmospheric and oceanic circulations,rotatingdisk systems,transport engineering(automobile breaks),geothermal extraction and many others.Viscous flow in rotating frame developed by linearly stretched plate was firstly explored by Wang.[1]He derived series solutions for velocity pro files by using perturbation in rotation-strength parameter.Rajeswari and Nath[2]examined time dependent flow past a stretchable surface in a revolving fluid.Nazar et al.[3]provided numerical approximations for unsteady flow over an impulsively stretched plate in rotatingfluid using Keller-box method.They also derived asymptotic solutions valid from large time,which were shown to be consistent with the numerical findings.Boundary layer flow of Ostwald-de-Waele(power-law)fluid in rotating frame was addressed by Kumari et al.[4]for broad range of power-law index.An analytical study for rotating flow of an electrically conducting second grade fluid past a porous shrinking sheet was presented by Hayat et al.[5]Abbas et al.[6]addressed the unsteadiness in revolving flow bounded by a stretchable wall using Keller-box method.Javed et al.[7]numerically explored the revolvingflow by an exponentially stretching sheet considering space dependent angular velocity in rotating frame.Later,Zaimi et al.[8]studied t?h′eflow induced by stretching surface in rotating Walters?aAZB liquid using a numerical scheme.Khan et al.[9]reported numerical simulations for nanofluidflow by a deformable surface in rotating frame considering two different thermal conductivity models.Recently,Mustafa et al.[10]described rotational effects on the laminar flow of Fe3O4-water ferrofluid caused by stretchable surface.In another recent article,exponentially stretchedflow of Maxwell fluid in rotating frame was modeled by Mustafa et al.[11]
Fluids which deform non-linearly upon the application of shearing forces are frequently encountered in industrial processes.Non-Newtonian behavior manifests itself in a number of ways.Shear-thinning/thickening effect is an interesting characteristic which is frequent amongst fluids such as blood,paints,polymers,colloidal solutions etc.Power-law model is a generalized Newtonian fluid model that has been widely applied for description of shearthinning or shear-thickening phenomenon. Some well-documented boundary layer problems concerning powerlaw fluids can be stated through the studies.[12?14]Another important property of non-Newtonian liquids is the retention of fading memory upon the elimination of shearing force known as fluid elasticity.Viscoelastic behavior refers to the situation in which motion of the material element not only depends on the current stress state but also on the deformation history of the element. Suchfluids display significant deviation from the Newtonian limit in terms of both physical behavior and computational complexity.Upper-convected Maxwell model is a viscoelastic fluid model that has been consistently used by the researchers due to its simplicity.Harris[15]presented the boundary layer equations for two-dimensionalflow of upper-convected Maxwell fluid.Sadeghy et al.[16]used these equations to explore Maxwell fluid flow driven by a moving rigid plate in stationary fluid.They employed numerical and perturbation approaches to determine the velocity distribution above the plate.Finite difference approach was found to be effective here in comparison to the other employed methods as it solved the problem for Deborah number as large as 2.4.Kumari and Nath[17]analyzed the Maxwell fluid flow in a region of stagnationpoint utilizing finite difference method.It was found that viscoelastic fluid parameter gives resistance to momentum transport phenomenon.Abel et al.[18]discussed the stretched flow of viscoelastic Maxwell fluid in the existence of Lorentz force.Hayat et al.[19]analytically explored the Maxwell fluid flow in the vicinity of stagnation-point with melting effects.Shateyi[20]proposed a numerical approach for tackling the Maxwell fluid flow with mixed convection and chemical reaction.Recent material in this direction can be stated through Refs.[21–30].
The objective of this paper is to investigate non-linear radiative heat transfer over a deformable surface placed in revolving Maxwell fluid.In many papers,the authors made use of linearized Rosseland formula to attain a linear energy equation,which brings no additional computational effort(see,for example Refs.[31–33]).Here the inclusion of non-linear flux provides strongly non-linear system,which enables one to determine the features of small/large temperature differences(see Refs.[34–37]for details).Accurate similar solutions are found for broad range of embedded parameters.Emphasis has given to the effects of viscoelasticity,rotating frame and radiative heat transfer on the solutions.
2 Problem Formulation
Consider a laminar flow above a stretchable surface placed in a rotating viscoelastic fluid obeying upperconvected Maxwell model.The surface lying in the plane z=0 is stretched with velocity uw=ax in which a>0 denotes the stretching rate and x stands for the distance measured from the origin.Fluid rotates about the vertical axis with uniform angular velocity ω(see Fig.1).We take into account the non-linear Rosseland formula for thermal radiation.The surface temperature Twis assumed to be greater than the ambient fluid temperature T∞.Under these assumptions,conservation equations for Maxwell fluid flow and heat transfer in rotating frame are:
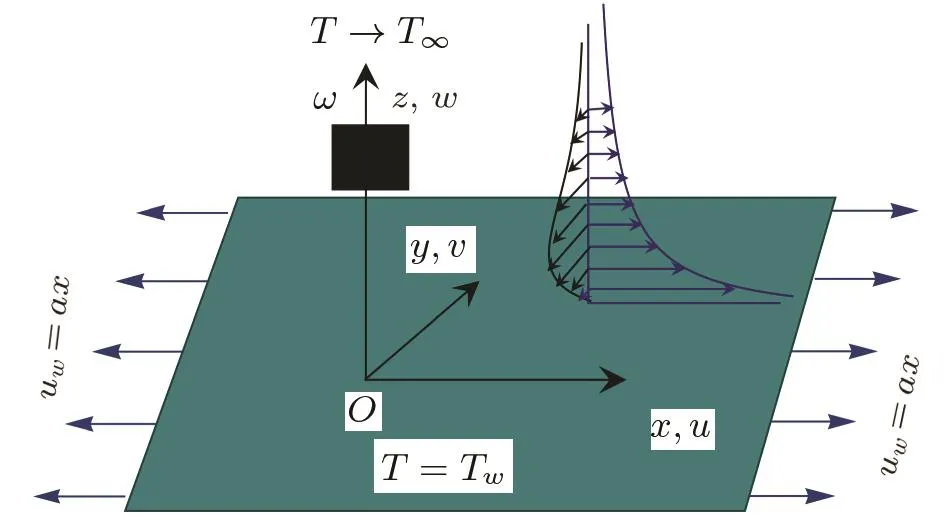
Fig.1 Physical con figuration and coordinate system.
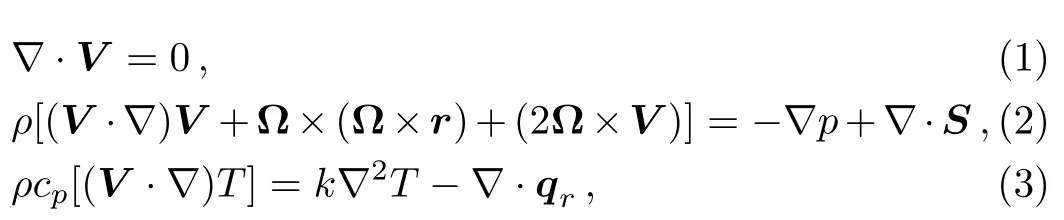
where ρ represents fluid density,cpdenotes the specific heat of fluid,k stands for thermal conductivity,? = [0,0,ω]the angular velocity vector and qr=?(4/3aR)grad(eb)is the heat flux due to radiation in which aR[m?1]represents the mean absorption coefficient and eb[W·m?2]the black body emissive power,which is related with the absolute temperature T by the Stefan-Boltzmann law as eb= σ?T4,with σ?=5.7 × 10?5W ·m?2·K?4as Stefan-Boltzmann constant.In Eq.(2),the term(2?×V)is due to the coriolis acceleration while the expression(? × (? × r))= ??(ω2r2/2)embodies centrifugal acceleration,which balances with the pressure gradient??p.The extra stress tensor S in Maxwell fluid obeys the following relation:
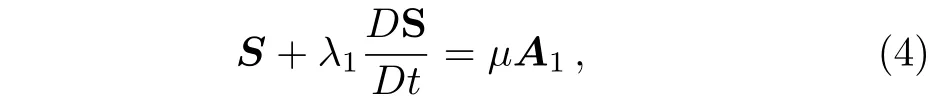
in which λ1is the fluid relaxation time,A1=(?V)+(?V)tthe first Rivlin-Ericksen tensor and D/Dt the upper-convected time derivative.Thus,component forms of Eqs.(1)–(3)under usual boundary layer approximations are given below:

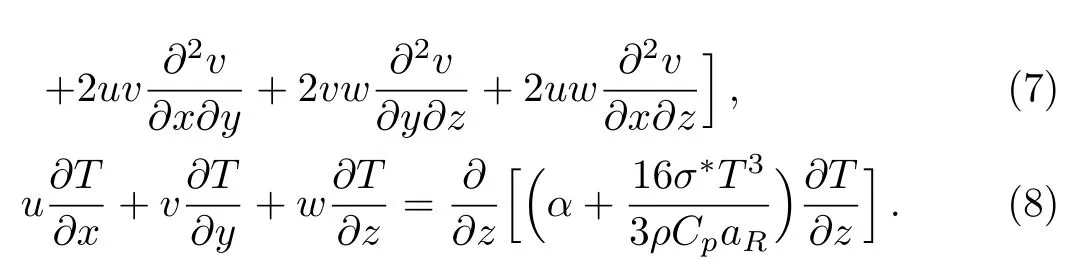
The boundary conditions in the present problem are as below:
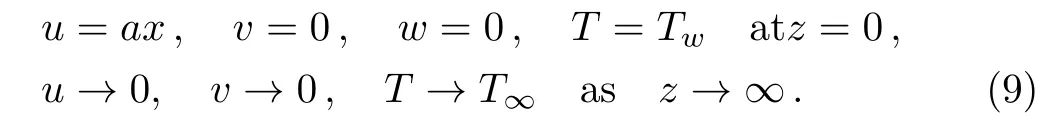
Introducing the following dimensionless variables
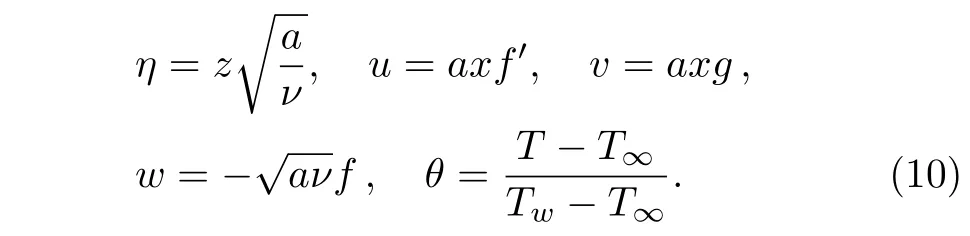
Equation(5)is identically satis fied and Eqs.(6)–(9)become
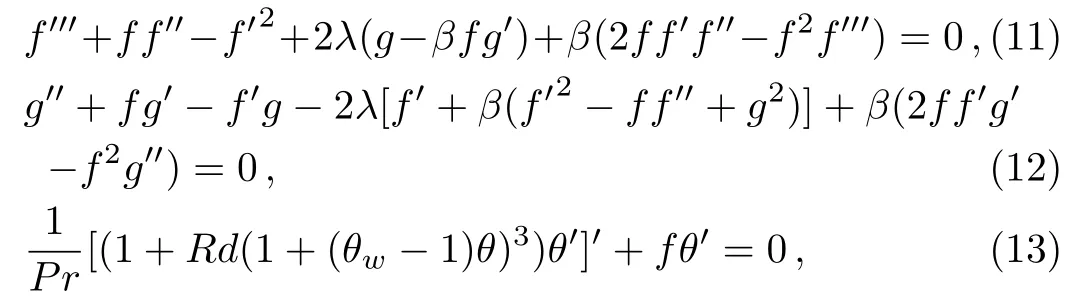
with transformed boundary conditions
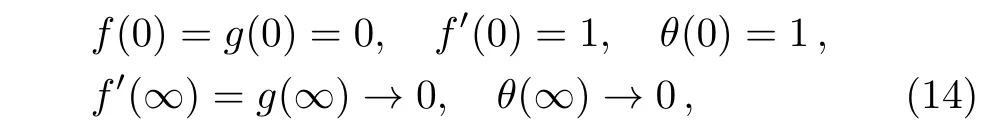
in which λ = ω/a is rotation-strength parameter,β = λ1a denotes the Deborah number,Pr= ν/α represents the Prandlt number,Rd=16σ?T3∞/3kaRstands for thermal radiation parameter and θw=Tw/T∞measures wall to ambient temperature ratio.When λ=0,the differential system(11)–(14)correspond to the case of non-rotating frame as discussed by Mushtaq et al.[18]Further,the case of Newtonian fluid is achieved by setting β=0. As pointed out in Ref.[29],present model reduces to linear radiation case when Rd is sufficiently small and θwapproaches unity.We define the local Nusselt number Nuxwith an aid of Fourier law as follows:
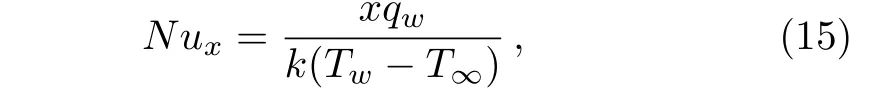
where qwis the wall heat flux at the surface due to both convection and radiation effects.It is given by:
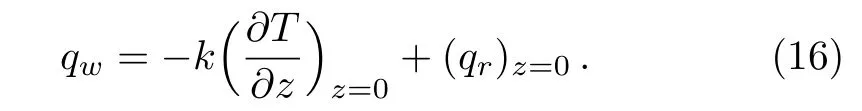
Now using(16)in Eq.(15)and then invoking the transformations Eq.(10),we get
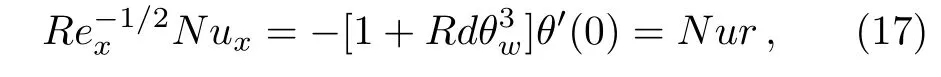
where Rex=uwx/ν is the local Reynolds number.
3 Numerical Results and Discussion
We employ the standard shooting technique to treat the coupled non-linear differential system comprising of Eqs.(11)–(14)numerically.The values of missing slopes f′′(0),g′(0),and θ|prime(0)are iteratively estimated through Newton-Raphson method.The validity of numerical scheme is ascertained by comparing the values of f′′(0)and g′(0)with those of already published papers in viscous fluid case(see Table 1).Table 1 shows that current computations almost match exactly with the results of previous studies at all values of rotation-strength parameter λ.Computational results of local Nusselt number Re?1/2xNux,which is related with the heat flux from the surface,are obtained for different values of λ,θwand β in Table 2.It is clear that the wall heat flux is reduced due to the inclusion of viscoelastic effects.We also observe a significant growth in heat transfer coefficient as the difference(Tw?T∞)enlarges.Moreover,like the viscoelasticity,fluid rotation also adversely affects the heat transfer from the plate.
The curve of f′related with the u-velocity component is computed for a variety of Deborah numbers in Fig.2.By definition,Deborah number signifies the ratio of fluid memory duration(relaxation time)to its characteristic time scale.It is encouraging that computational treatment proposed in this work can furnish convergent results up to Deborah number 1.8.It is evident that curve f′begins from unity at η =0 and tends to zero as η → ∞.Another noticeable behavior is that the velocity u approaches to zero at smaller distance from the sheet when β becomes large.In other words,hydrodynamic boundary layer shrinks as the stress relaxation duration enlarges.This result is consistent with the findings of previously published articles(see Abel et al.,[18]Shateyi,[20]Hsiao[21]etc.for details).In accordance with Ref.[21],an increasing trend in surface velocity gradient f′′(0)is apparent for growing values of Deborah number β.This follows from the fact that increasing values of parameter β implies slower recovery process,which in turn slows down the development of boundary layer.
Figure 3 predicts the influence of rotation-strength parameter λ on the function f′.The parameter λ compares the rotation and stretching rates.It is realized that velocity field f′decreases exponentially with an increase in η in non-monotonic fashion when larger values of λ are employed.More precisely,we observe oscillatory pro file of f′for large value of λ.Further,the pro files shift towards the stretching boundary when λ enlarges indicating that boundary layer thickness is reduced due to the consideration of rotating frame.
In Fig.4,velocity pro file is plotted at different values of Deborah number β for a specified value of rotationstrength parameter λ.The velocity component g(η)is non-zero and it has a negative value signaling that fluidflows in negative y-direction only.This outcome is anticipated due to the inclusion of rotational effect.It is also clear that function g(η)has an oscillatory decaying pro file for any non-zero value of λ.The envelope of oscillations grows further as the angular velocity is enhanced.A cross over is apparent in the pro files of g(η)illustrating that velocity in y-direction increases near the wall and decreases far from the wall as parameter β enlarges.This outcome is different from the effect of viscoelastic parameter of second grade fluid.
In Fig.5,the change in velocity pro file g(η)with the variation in λ is observed.This figure shows that the function g(η)has pro file analogous to the function ?ηexp(?η)for smaller values of λ while it decays oscillatory when larger values of λ are considered.This outcome has also be noticed by Nazar et al.[3]and Zaimi et al.[8]

Table 1 Comparison of results for f′′(0)and g′(0)with those of Wang[1]and Zaimi et al.[8]for various values of λ when β =0.
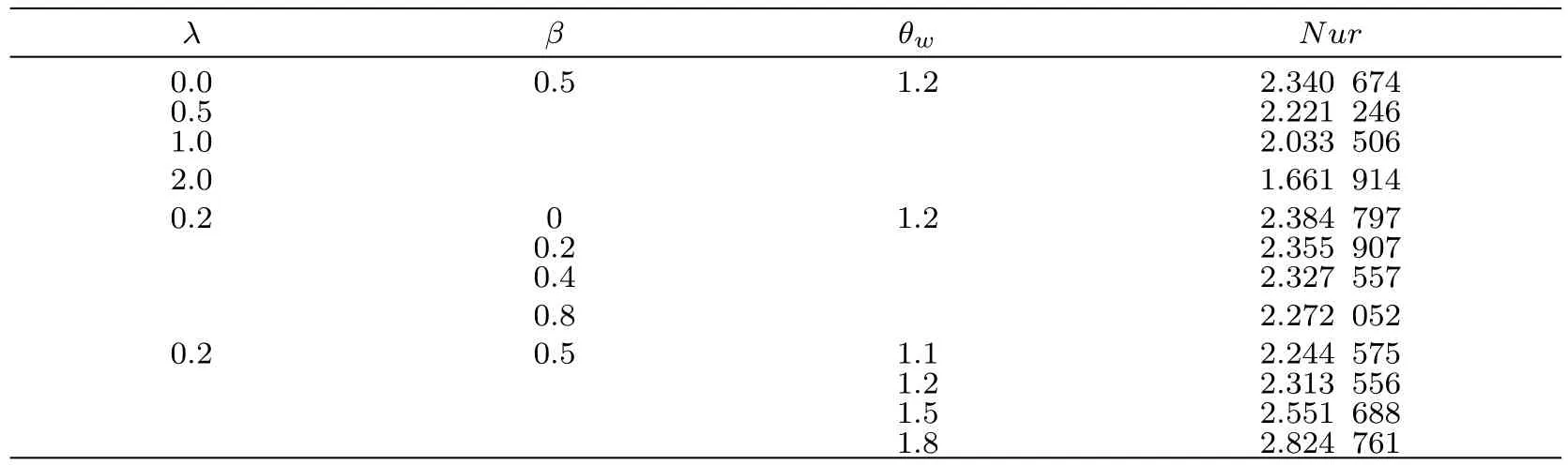
Table 2 Computational results of local Nusselt number Nur= ?[1+Rdθ3w]θ′(0)for different values of λ, β,and θwwhen Rd=0.5 and Pr=7.
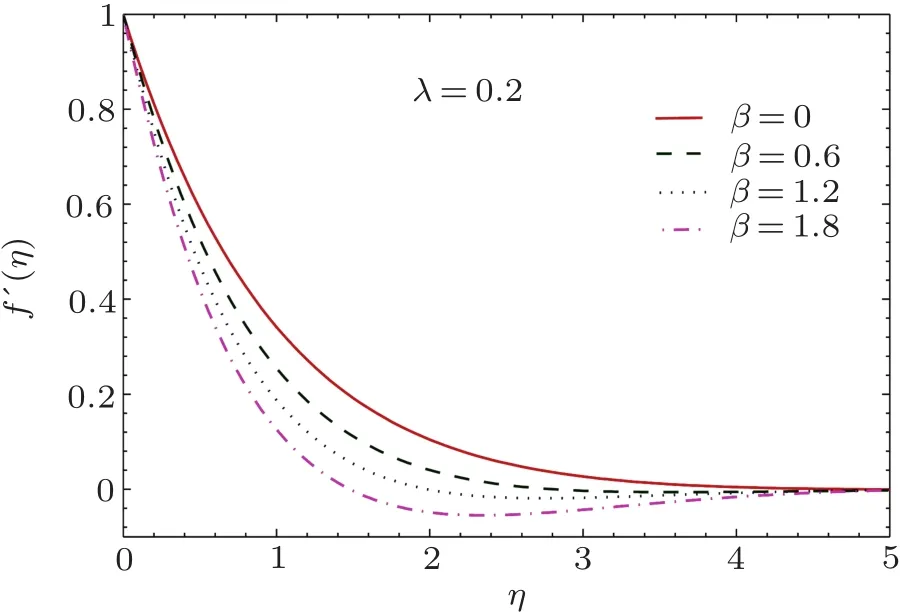
Fig.2 Curves of velocity field f′(η)for different values of β.
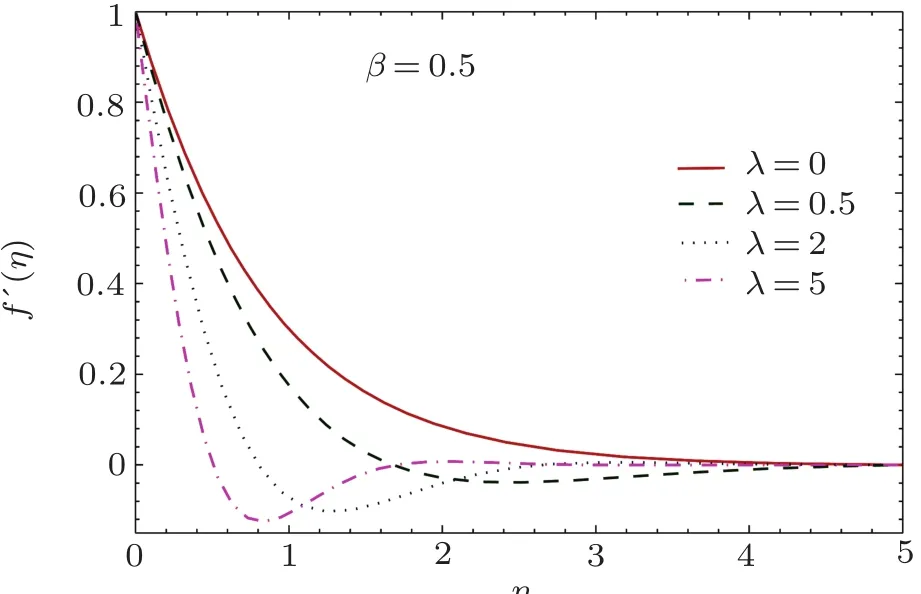
Fig.3 Curves of velocity field f ′(η)for different values of λ.
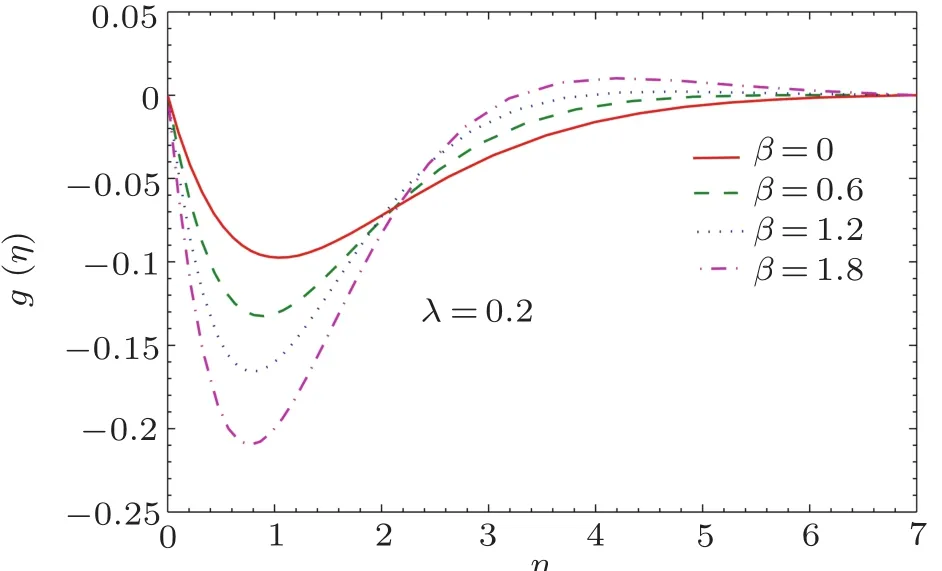
Fig.4 Curves of velocity field g(η)for different values of β.
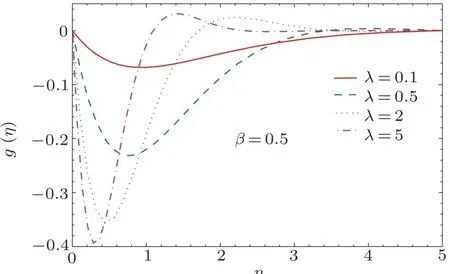
Fig.5 Curves of velocity field g(η)for different values of λ.
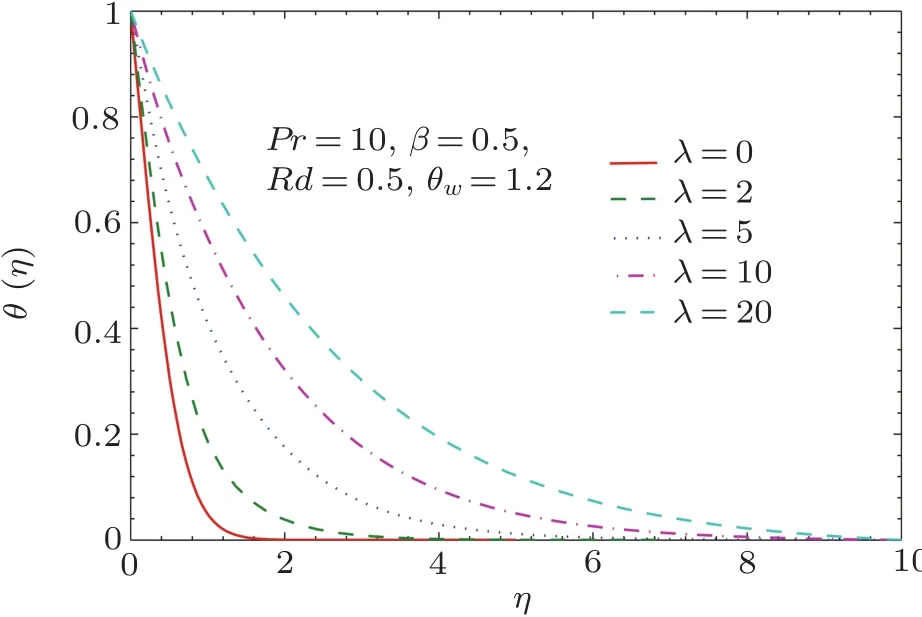
Fig.6 Pro files of temperature θ(η)for different values of λ.
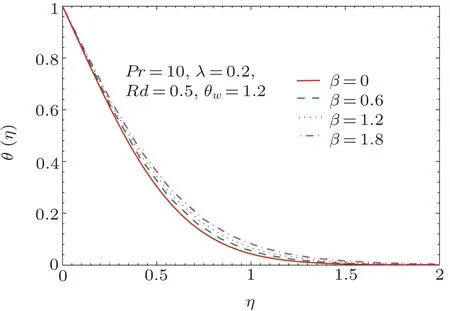
Fig.7 Pro files of temperature θ(η)for different values of β.
Figure 6 portrays temperature pro file θ at various values of rotation-strength parameter λ.There is a significant rise in temperature θ when rotation-strength parameter is varied from λ =0 to λ =10.The resistance to the fluid motion o ff ered by the rotating frame enhances the temperature.As demonstrated in Wang,[1]the entrainment velocity decreases for increasing values of λ.Thus intensity of cold fluid drawn towards the stretching surface reduces with increasing λ.As a consequence,thermal boundary layer expands when larger values of λ are accounted.
On the other hand,temperature θ slightly rises and penetration depth grows when Deborah number β is incremented(see Fig.7).Moreover,slope of temperature pro file near the wall appears to decrease upon increasing β.This behavior is described as follows.Our computations revealed that vertical velocity is inversely proportional to the Deborah number β.It is therefore anticipated that amount of cold drawn in the vertical direction will reduce when parameter β enlarges.This in turn leads to the thickening of thermal boundary layer and enhancement in surface heat transfer rate.

Fig.8 Pro files of temperature θ(η)for different values of θw.
Figure 8 elucidates the behavior of temperature ratio parameter θwon the temperature pro file.As θwenlarges,that is,the parameter related with the ratio of wall temperature to the ambient temperature increases,the temperature pro file increases. From Eq.(10),it can be noticed that effective thermal diffusivity αeff=(α +16σ?T3/3ρCpk?)is temperature dependent due to the inclusion of non-linear heat flux.As also observed in Refs.[34-36],temperature distribution has S-shaped pattern against the similarity variable in the limiting case as θw→ ∞.Thus governing system(13)–(16)correspond to the adiabatic case(θ′(0)=0)when ratio(Tw/T∞)tends to in finity.
Figure 9 shows the temperature pro files for varying radiation parameter Rd.Temperature pro files become thicker and temperature gradient at the surface enlarges when Rd is incremented.Similar behavior of radiation parameter was also figured out by Hsiao.[32?33]In linear radiation situation,temperature distribution approaches a constant finite value as Rd→0.However,such effect is not preserved in non-linear radiation model.
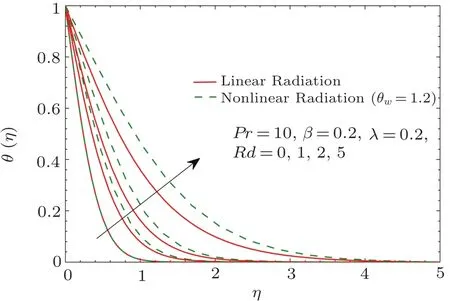
Fig.9 Pro files of temperature θ(η)for different values of Rd.
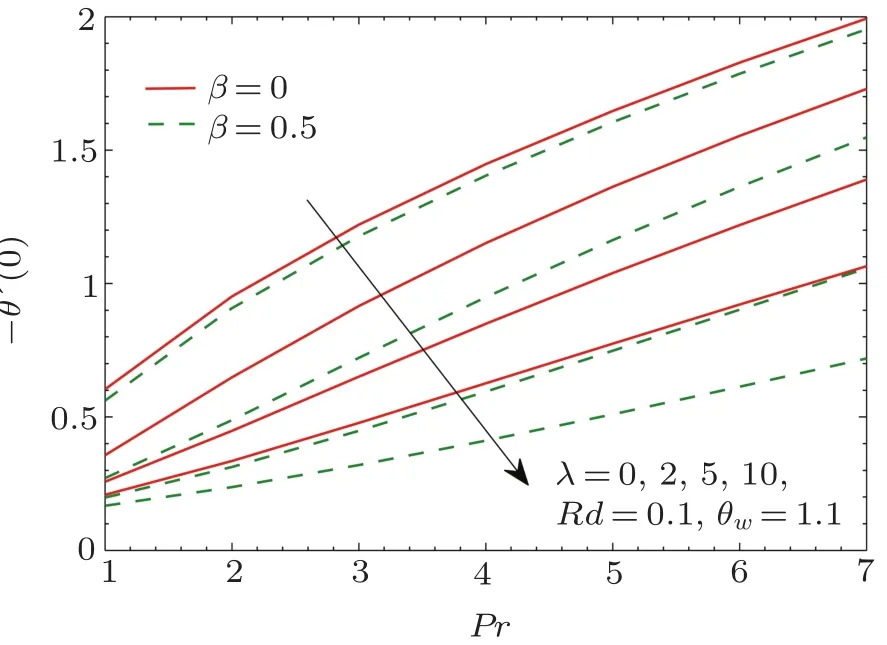
Fig.10 Pro files of local Nusselt number ?θ′(0)for different values of λ.
In Fig.10,we plot wall temperature gradient θ′(0)as a function of Prandtl number Pr at different values of λ.Larger Prandtl number fluids are effective in heat convection compared to pure conduction.Due to this reason θ′(0)shows an increasing trend when Pr is increased and it tends to zero for vanishing Pr.Furthermore,there is a decrease in θ′(0)as β increases from β =0 to β =0.5.Interestingly,this change becomes pronounced when rotation rate becomes larger in comparison to the stretching rate.
4 Conclusion
In this study,Maxwell fluid flow in rotating frame is discussed in the existence of non-linear thermal radiation.Similarity solutions are found for a broad range of thermal radiation parameter.The key aspects of this work are summarized below:
(i)Present numerical results are consistent with the previously published results for all values of rotationstrength parameter λ when β =0.
(ii)An increase in rotation-strength parameter leads to an enhancement in the heat penetration depth.
(iii)Dissimilar to the non-rotating frame,the decay in f′(η)with η is exponentially non-montonic.Indeed,there is an oscillatory pattern in the pro files of f′and g for non-zero values of λ.
(iv)As wall and ambient temperature difference becomes,a decrease in wall heat transfer coefficient and an increase in heat penetration depth occurs.Also,temperature distribution becomes S-shaped or θ′(0) → 0 as θw→∞.
(v)Fluid velocity in z-direction far from the stretching wall is reduced when rotation-strength parameter is increased.
(vi)The amount of cold fluid drawn in the vertical direction towards the stretching surface reduces for increasing values of β.This in turn leads to a reduction in heat transfer rate.
[1]C.Y.Wang,Zeitschrift fur Angewandte Mathematik and Physik 39(1988)177.
[2]V.Rajeswari and G.Nath,Int.J.Eng.Sci.30(1992)747.
[3]R.Nazar,N.Amin,and I.Pop,Mech.Res.Commun.31(2004)121.
[4]M.Kumari,T.Grosan,and I.Pop,Tech.Mech.1(2006)11.
[5]T.Hayat,T.Javed,and M.Sajid,Phys.Lett.A 372(2008)3264.
[6]Z.Abbas,T.Javed,M.Sajid,and N.Ali,J.Taiwan Inst.Chem.Eng.41(2010)644.
[7]T.Javed,Z.Abbas,M.Sajid,and N.Ali,Int.J.Numer.Meth.Heat and Fluid Flow 21(2011)903.
[8]K.Zaimi,A.Ishak,and I.Pop,Appl.Math.Mech.-Engl.Ed.34(2013)945.
[9]J.A.Khan,M.Mustafa,and A.Mushtaq,Int.J.Heat Mass Transf.94(2016)49.
[10]M. Mustafa, A. Mushtaq, T. Hayat, and A. Alsaedi, PLoS ONE 11 (2016) e0149304,doi:10.1371/journal.pone.0149304.
[11]M.Mustafa,R.Ahmad,T.Hayat,and A.Alsaedi,Neural Comput.&Appl.29(2018)493.
[12]Y.Lin,L.Zheng,and X.Zhang,Int.J.Heat Mass Transf.77(2014)708.
[13]Y.Lin,L.Zheng,X.Zhang,et al.,Int.J.Heat Mass Transf.84(2015)903.
[14]S.Xun,J.Zhao,L.Zheng,et al.,Int.J.Heat Mass Transf.103(2016)1214.
[15]J.Harris,Rheology and Non-Newtonian Flow,Longman Publishing Group(1977).
[16]K.Sadeghy,A.H.Naja fi,and M.Saffaripour,Int.J.Nonlinear Mech.40(2005)1220.
[17]M.Kumari and G.Nath,Int.J.Non-linear Mech.44(2009)1048.
[18]M.S.Abel,J.V.Tawade,and M.M.Nandeppanavar,Meccanica 47(2012)385.
[19]T.Hayat,M.Mustafa,S.A.Shehzad,and S.Obaidat,Int.J.Numer.Meth.Fluids 68(2012)233.
[21]K.L.Hsiao,Arabian J.Sci.Eng.39(2014)4325.
[22]A. Mushtaq, M. Mustafa, T. Hayat, and A. Alsaedi, J. Aerosp. Eng. 27 (2014) doi:org/10.1060/(ASCE)AS.1943-5525.0000361.
[23]J.A.Khan,M.Mustafa,T.Hayat,and A.Alsaedi,PLoS ONE 9(2015)doi:10.1371/journal.pone.0137363.
[24]M.Awais,N.Muhammad,T.Hayat,and A.Alsaedi,Int.J.Non-linear Sci.Numer.Simul.16(2015)123.
[25]M.Mustafa,J.A.Khan,T.Hayat,and A.Alsaedi,AIP Advances 5(2015)doi:10.1063/1.4916364.
[26]T.Salahuddin,M.Y.Malik,A.Hussain,et al.,J.Mag.Magnet.Mater.401(2016)991.
[27]A.Mushtaq,S.Abbasbandy,M.Mustafa,et al.,AIP Advances 6(2016)doi:10.1063/1.4940133.
[29]K.L.Hsiao,Appl.Therm.Eng.112(2017)1281.
[30]A.Mushtaq,M.Mustafa,T.Hayat,and A.Alsaedi,Int.J.Non-linear Mech.79(2016)83.
[31]L.Zheng,C.Zhang,X.Zhang,and J.Zhang,J.Franklin Inst.350(2013)990.
[32]K.L.Hsiao,Energy 59(2013)494.
[33]K.L.Hsiao,Comp.Fluids 104(2014)1.
[34]A.Pantokratoras and T.Fang,Meccanica 49(2014)1539.
[35]M.Mustafa,A.Mushtaq,T.Hayat,and B.Ahmad,PLoS ONE 9(2014)doi:10.1371/journal.pone.0103946.
[36]M.Mustafa,A.Mushtaq,T.Hayat,and A.Alsaedi,J.Taiwan Inst.Chem.Eng.47(2015)43.
[37]A.Mushtaq,M.Mustafa,T.Hayat,and A.Alsaedi,Int.J.Numer.Meth.Heat Fluid Flow 26(2016)1617.
 Communications in Theoretical Physics2018年4期
Communications in Theoretical Physics2018年4期
- Communications in Theoretical Physics的其它文章
- Effects of Low Anisotropy on Generalized Ghost Dark Energy in Galileon Gravity
- Numerical Study of Mixed Convective Peristaltic Flow through Vertical Tube with Heat Generation for Moderate Reynolds and Wave Numbers
- Melting Heat in Radiative Flow of Carbon Nanotubes with Homogeneous-Heterogeneous Reactions
- Controlling Thermal Conduction by Graded Materials?
- Direct Urca Processes Involving Proton1S0Superfluidity in Neutron Star Cooling?
- Effects of a Weakly Interacting Light U Boson on Protoneutron Stars Including the Hyperon-Hyperon Interactions?
