Developing Mathematics Games in Anaang

Itoro Michael

University of Uyo, Nigeria

Mfon Brownson Ekpe

University of Calabar, Nigeria

1. Introduction

Anaang is a non-major linguistic group but, with a rich socio-cultural heritage. Its culture exists dominantly in oral form. Only very few aspects of the cultural heritage have been documented, while the greater part has gone into extinction, with many more aspects endangered. This is owing to the attitude of the people toward indigenous culture, due to the influence of the high level of shift toward the cultures of developed countries.One of the aspects of Anaang culture that is highly endangered is its indigenous games,specifically, the mathematics games.

Mathematics games are aspects of Anaang verbal art that are used by both children and adults for learning, entertainment and recreation. In other words, they are a form of folk ideas that are embedded in African verbal art. Mathematics games are regarded as verbal art because this genre is yet to be fully documented and whatever is in existence does not have any form of authorship (Michael, 2013; Finnegan, 2012). Since they exist dominantly in an oral form, there is a tendency for some of the games to degenerate with time if they are not documented. Although games themselves are central to the humanities,some elements of calculation are involved to make the games competitive. In other words,some games require the knowledge of some interesting aspects of mathematics, hence the term ‘mathematics games’. This paper therefore sets out to analyse selected games in Anaang that have certain concepts of mathematics with the main aim of providing insights into the interaction between mathematics concepts and culture.

It should be noted that mathematics is exclusively a genre of science, while game is exclusively a genre of humanities studies. Nevertheless, mathematics ideas like calculation, numeration, addition, subtraction, multiplication, fractions, ratios, Highest Common Factor (HCF), Least Common Multiple (LCM), number facts, etc., are explored and used in various activities of games.

The general notions of games in both Western and African cultures have received high levels of research. Most of the games are well documented in both electronic and print media. The Western games are well developed and used for both formal and informal activities (Ferdig, 2009). However, mathematics games are a more restricted aspect of games which have not received wider research or documentary attention in Nigerian culture. This has resulted in the degeneration of most of these games. That being said,scholars have made some positive effort towards the development of African mathematics games, which can be found in research journals and monographs. Some of these publications include: Amstrong and Bamgbose (1971), Adenegan and Adedoye (2017),and Etuk (1967) for Yoruba, Bohannan (1953) for Tiv, Crowe (1982) for Benin, and Musa(1987), Mohammed, Ibrahim, and Hatiru (2010) for Hausa. We also have publications by Ascher (1990), Crowe (1982), Doregowski (1972), Booth (1975), Campbell (1977), and Mereku (2012) on African mathematics games.

With the introduction of the theory of ethnomathematics, the use of African mathematical games in formal settings is gradually being unraveled by researchers.

This is evidenced in recent publications by Sumbi and Bassey (2013), Mereku (2012),Stephen and Carry (1994), and Habibu (2015). Publications such as these have triggered a high level of interest in mathematics games. Comparatively, the Western mathematical games/rhymes seem to dominate formal settings even in Africa, while African games are restricted to informal settings, probably because of the availability of a wide range of the print/electronic materials of Western games. It should, however, be emphasized that although African games exist dominantly in oral form, the genre has certain aspects that relate directly to mathematics concepts. These aspects contribute greatly to outdoor mathematics activities. According to Bishop (1988), the use of concepts in activities like counting, locating, measuring, designing, playing and explaining in games is culturally universal. Therefore, these activities can be applied to make mathematics meaningful and interesting. This idea also echoed in Orey and Rosa (2006), Davis et al. (2008), and Zhang and Zhang (2010). These authors are all of the view that these activities are vital in the development of mathematical ideas in African games for indoor activities. There is therefore the need to develop more African mathematics related games for indoor activities, including the learning of mathematics, especially in a developing linguistic area, such as Anaang. Therefore, the objectives of this research are:

To unravel the mathematics ideas inherent in the selected games and the relevance of these games in the understanding of some aspects of mathematics like numeration, calculation,factorization and number facts.

To relate the relevance of mathematics ideas to cultural development in Anaang vis-à-vis Africa, and to harness the relevant activities of African culture with mathematical concepts.

To analyse the steps employed in the performances of Anaang mathematics games. Since this research is interdisciplinary in nature, it will go a step further to bridge the gap between language, recreation and science.

It should, however, be observed that since children are fast to assimilate numbers, words,sentences and figures in short songs/rhymes and games, the development and adoption of the concepts of mathematics related games will add flair to the understanding of mathematics by children, thereby making mathematics recreational for both outdoor and indoor activities.This will, in turn, enhance more interests in research, learning and publications, preserve these games from extinction, strengthen the endangered games and open avenues for intergenerational transmission/ transposition of the rich African cultural heritage.

Although this work is purely descriptive and presentation based, the theory of ethnomathematics, which centres on the interface between mathematics and culture, is adopted for analysis.

2. Mathematics Games

Mathematics game is a concept derived from the combination of the concepts of mathematics and game. While mathematics is an aspect of applied science, games are a genre of culture. These two ideas stem from the theory of ethnomathematics. The word ‘game’contains a variety of notions, which include recreation, competition, sportsmanship,winning, and losing, among others (Mereku, 2012; Gerdes, 1989). It also cuts across the concepts of children’s play, puzzles, team sports, board games and card games (Asher,1990). As observed by some scholars (Bishop, 1988; Zhang & Zhang, 2010), mathematics games involve games whose rules, strategies, and outcomes are defined by clear mathematical parameters. This shows that there is an interplay between mathematical ideas and culture in such a way that they cannot be separated from each other.

James (1982) looked at mathematics games as puzzles that require solutions, and put forward that it is the act of solving these puzzles that adds fun to this genre. He therefore defined this concept as a form of puzzles, magic tricks, or any mathematical activity that provides amusement, joy, and reduces tension or boredom (p. 27). His focus was on the pedagogic implications of these games. Contrary to this view, Gerdes (1989) noted that mathematics games at some point are different from mathematics puzzles. Mathematics puzzles require specific mathematical expertise to complete the puzzle, whereas mathematics games do not require deep knowledge of mathematics for participation.

As observed earlier, the important aspect of a game is fun, without which it would be very boring and highly discouraging. There is a high level of involvement in games coupled with excitement, motivation, concentration, positive thinking, steady memorization and quick understanding. As observed by James (1982) and Zaslavsky(1973), mathematics ideas cut across indigenous culture in areas such as recreation,language, and craft. In other words, indigenous culture interacts with mathematics for the building of knowledge. For instance, some aspects of traditional bargaining in markets require a fair knowledge of mathematics. The acts of multiplying the unit cost with the quantity, cash payment, partial payment, balance payment, and measuring of clothing materials, beef, chicken, and crayfish require the knowledge of the culture of the people.This in essence shows that there is an interaction between mathematics and culture. There are specific aspects of the African as well as Anaang culture that are highly entertaining,recreational and brain awakening. These aspects manifest highly in songs, dances, tales,arts, crafts, sports and games. Unfortunately, most of these aspects are extinct; many more are endangered, while a greater number are threatened.

Generally, mathematics ideas in culture are not explicit mathematics. They are often intertwined with arts, crafts, riddles, puzzles, games, graphics, and other aspects of verbal art. These aspects, as observed by Gerdes (1994), hide the traditional mathematics ideas. Although these ideas are said to be hidden, they are useful in the development and patterning of mathematics concepts like number facts, time, brain awakening, and pattern production. The genre is also seen as a useful tool for edge-cutting and river-crossing(Ascher, 1990; Booth, 1975; Crowe, 1975). This shows that mathematics games are an interdisciplinary genre that bridges the gap between science (mathematics) and culture(games). We shall therefore present data in Anaang on selected mathematics games,using the theory of ethnomathematics for our analysis, to bridge the gap between African culture and mathematics with an emphasis on Anaang culture.

3. Theoretical Approach

The learning of mathematics entails the interaction of mathematical ideas, signs, objects,and the construction of meanings using language as a medium. This entails a multimodal approach. Although mathematics’ meaning seems to be relative to the individual’s understanding, the object of mathematics is treated as ‘conceptual forms of historically,socially, and culturally embodied reflective, mediated activity’. In this case, Hoffman(2006) concludes that the learning of mathematics actually involves ‘concepts of activity’.

The activity of mathematics is performed by means of visible signs, while the knowledge of mathematics is developed by interpreting and transforming signs, which is central to semiotics. In semiotic studies, meaning depends on interpretation. By emphasizing the dependence of meaning on interpretation, Hoffman (2006) observed that this will create the assumption that all mathematical meanings seem to be relative to the individual’s interpretation of mathematical signs. The common grounds in this paper therefore centres on how the concepts of culturally mediated symbols in African games and their representation can be related to the knowing, interpreting, and learning of certain mathematical concepts.

Communication and interaction are central in the interpretation of games.Interpreting games is defined as ‘a(chǎn) constructed interpretation process’ by classroom participants (Otte, 2003, p. 211). Therefore, getting students engaged in interpreting games is one of the major challenges confronting the teaching of mathematics games.In mathematics, children learn to operate with signs and objects. As observed by Otte(2003), communication, interaction, and interpretation in mathematics are mediated by a set of signs, rules of sign production, and a set of representation between the signs and their meanings (p. 210). The learning of mathematics is not only a cognitive process, it also entails activities performed in social interaction. In view of the importance of signs and representation for mathematics, mathematics is therefore seen as a genuinely semiotic science (Hoffman, 2006). To learn mathematics from a semiotic perspective, the problem of the interpretation of signs must be taken into consideration. The field of semiotics relates meaning to the concepts of mathematics inherent in the selected African games as presented in section 4 of this work, using the framework of ethnomathematics.

The theory of ethnomathematics proposed by D’Ambrosio (1977) is adopted here for the description and analysis of Anaang mathematics games. Since the development of the theory of ethnomathematics in the 1970s, more and more researchers have applied it in diverse perspectives, leading to the invention of diverse but related concepts. For instance,D’Ambrosio (1982, 1984, 1985) defined ethnomathematics as a form of mathematics which is practiced among identifiable cultural groups, such as national-tribal societies,labour groups, children of certain age brackets and professional classes. He used the term ‘spontaneous mathematics’ to drive home the fact that the games are developed in a spontaneous form, but one that is relative to the culture of the people. Other terms used for his genre are ‘street mathematics’, ‘informal mathematics’, and ‘oral mathematics’(Carraher, 1988; Ascher & Ascher, 1981; Davis et al., 2008). This implies the fact that ethnomathematics is learned outside of formal classroom settings. In other words, this form of mathematics is practiced in an informal setting. The ideas are yet to be properly documented, hence the term ‘oral mathematics’ (Carraher, 1988; Kani, 1992). In its application, the ideas used for this mathematics are adopted from folk concepts, which therefore gives room to the term ‘indigenous mathematics’ (Gay & Cole, 1967; Zaslavsky,1973). Orey and Rosa (2006) looked at ethnomathematics as the people’s mathematics,based on the fact that it is culture-based, while Gerdes (1984, 1985, 1986, 1990, 2000),called it hidden or frozen mathematics, in the sense that traditional mathematical ideas are not explicitly expressed in games. He added the term ‘suppressed/oppressed mathematics’to support the view that traditional mathematical ideas have been completely suppressed by the colonial occupation of the third world. If the genre is not revitalised, it can go into extinction, decay, or die, especially where there is no intergenerational transmission.

Ethnomathematics or ethnomathematicology (Gerdes, 1985, 1994) is the field of inquiry that studies mathematical ideas in their histo-cultural contexts, including understanding the role and embodiment of mathematical thinking both in the invention and(re)production of decorative patterns. For him, mathematical thinking is as pan-human as using language or music to play, listen, and feel, which is seen as a product of culture.

Generally, ethnomathematics is a term which is used to show the relationship between mathematics and culture. It is seen as the mathematical ideas of the people in traditional cultures, since it is a form of mathematics without any written expression, practiced among identifiable cultural societies ranging from distinct numerical mathematical systems to cultural mathematics education. In the following section, we shall adopt this theory for the description of mathematics-related games in Anaang.

4. Anaang Mathematics Games

As mentioned elsewhere in this paper, the notion of mathematics games here is restricted to selected games that have some elements of mathematics-related concepts in Anaang.The games are:eto (rhythm in stick-beat game), tinka (yes/silence game),mkainuun mkpainuun (pebble-in-fist game), nsa(airborne pebble game), nsa ikpe(pebble-in-circle game), and nsa(messenger pebble game). The presentation is purely diagrammatic, without any pictures. The essence is that the data was not collected for documentary purposes. This is part of an on-going larger research on Anaang folklore;therefore the omitted details shall be the focus in further research.

4.1 Game 1. (Rhythm in stick-beat game)

This game is a singing game which makes use of stick-beats to produce a uniform rhythm.

It involves a minimum of five players and short sticks as shown in fig. 1. The number of the sticks is in equal proportion with the number of players.

Figure 1. A representation of the positions of the players numbering 1-5 in the game

The leader is player number 1 (pl 1) followed by pl 2, pl 3, pl 4, while the last person is pl 5. The arrow shows the direction of the stick movements.

The leader holds all the sticks and chantswhile all others will respond

The song is followed by a rhythm produced by the stamping of the palms on the floor.The leader releases the sticks one by one to the nearest person to his right. The stick is passed on to the next person, who passes it to the next person in that direction. The leader continues to release all the sticks while the following persons continue to pass them on.

When the leader is left with only one stick, the evaluation starts, in the sense that everybody has, at that instance, been given equal opportunity to compete. As the rhythm heightens, all the players are expected to have one stick each in their hands. The passing continues, following the rhythm of the song. The stick is not passed on to the next person at random, it is done in a uniform way, in order to maintain the steady rhythm.

The laws of the game are:

? Nobody should have more than one stick in his hand.

? The stick should be passed in an anti-clockwise direction.

? All players must maintain a uniform pattern of the tap-and-beat in order to produce a rhythm.

? At the peak of the game, any player that misses the beat/rhythm will end up with more than one stick. This will result in the disruption of the passing pace/distribution, thereby robbing the next person of a stick-beat.

? The one who has more than one stick is declared a loser and is dropped, while others continue in the competition.

? The disqualification of a candidate triggers the reduction in the numbers of the sticks. More and more sticks are dropped based on the numbers of candidates that are disqualified.

When a candidate is disqualified, there is a brief pause before the game resumes. The game continues in that pattern until a winner emerges. It should, however, be noted that as candidates are disqualified, they can devise means to distract others in a way that many candidates are bound to violate the laws of the game because of the distractions, and become disqualified. The fun lies in the lyrics of the song, which is composed in the form of tongue twisters. The stick-beat is highly rhythmic and as such adds flair to the game.

4.1.1 Mathematics implication

The game has both mathematical and theoretical undertones.

i. First, it could be applied in the teaching of the calculation of counting, and the concept of the Least Common Multiple (LCM). For instance, if eleven persons are involved, it also involves the use of eleven sticks.

ii. The sticks must first be counted to match with the number of participants, and shared between the number of participants at the ratio of 1:1. At the point of sharing, the Least Common Factor there, is 1, 11. One can therefore multiply one stick by the eleven (number of players), to arrive at the total numbers of the required sticks.

iii. The numbers of sticks continue to decrease in proportion to the numbers of persons that are disqualified from playing. This is an example of subtraction and deduction methods.

iv. The game starts with a rhythm produced by the stamping of the palms on the floor. All the players continue to stamp their palms, while getting ready to grab the stick. The last person can tell the number of moves the stick makes by counting the number of beats he has made before the stick reaches his position.

v. The children could be made to count from 1-20 using sticks. They could also use the same set of sticks for division, manipulation of numbers, multiplication and numbering. The leader numbers the sticks to rhyme with the numbers of the players, and divides them into the numbers of the players to arrive at the number fact, which must be in equal proportionto the numbers of players.

The fun becomes heightened at the point of the violation of the rules of the game, as defaulters continue to be dropped. The rhythmic and the anti-clockwise uniform passing of the sticks are highly recreational for both participants and spectators. The wordis an ideophone, which depicts the sound of the movement of the sticks. Children derive joy at the sound of the stick-beat movement and the rhythm. Full concentration is paid by the audience and participants in order to maintain the steady flow of the game with minimal disruptions and to spot defaulters.

4.1.2 Theoretical implication

The role of the game is likened to the concepts of ranking and evaluation in the Optimality Theory formulated by Prince and Smolensky (1993) in theoretical linguistics. It’s a competitive process where all candidates are involved in the game. Each candidate is entitled to one stick. There are a set of constraints, ranked in order of hierarchy. The higher ranked constraint in this game involves a ‘mandatory one-stick maximum’, followed by the anti-clockwise movement of the sticks, stick-beat rhythm, no empty palm, while singing and the rolling of the sticks are the least in the hierarchy. The hierarchy is ranked as shown:

one stick maximum ＞ anti-clockwise movement of the sticks ＞ stick-beat rhythm ＞ no empty palm ＞ rolling the stick.

The violation of the rhythm is not as fatal as the violation of the number of sticks in one’s hand. Failure is based on the violation of the higher ranked constraint. The candidate with the highest violation of the rule is eliminated from the game. The elimination continues as more and more violations are committed.

The candidate that complies with the rules of the game to the end emerges as the winner in the competition.

4.2 Game 2.(Yes/silence game)

This game is a question/response rhyme played by a minimum of five players. The response is either yes or no. The items used for the query are ‘flying icons, and mammals’. The question is ‘can … fly?means yes, ‘silence’ means no. The next question is ‘can… give birth? The leader must have a list of animals, insects, and birds in his mental lexicon and use that to verbalise the rhyme.

There is no ordered way of listing, but the leader must design his tokens to make them melodious by taking two to three flying objects at the beginning before mixing them up.

The game starts with a salutation’ and the response isThe leader greets the group and the group responds to show their readiness. The leader verbalises the call, while other participants respond. (This is shown in example 2.)

The items in the series are: fowl, bush fowl, goat, bird, dog, cockroach, toad, hawk,tortoise, lion, cow, crow, and fly.

When an object is mentioned, the participant will affirm that it belongs to that set by either responding ‘tinˉka’ or keeping silent to refute the query. As the game progresses, the players introduce more tongue twisters like lai lai/kpai kpai for ‘no’ to add colour to the game. Any player who gives a wrong response is fired.

The question can move from flying objects to mammals as shown:

The items are: goat, lion, pig, bird, antelope, cockroach, hawk, cat, and dog. The query is‘can any of these objects give birth?’ The response is still either yes or no. The leader will continue until there is a loser. A player who keeps silent for ‘yes’ or breaks the silence for‘no’ is the loser and takes over as the leader. One can say that the game is highly exciting.

It involves a proper understanding of the structure of the object mentioned in order to get the right answer. The difference between the mammal and the bird is that mammals can give birth, but birds lay eggs.

The game requires some brain work and full listening attention to capture the icons used for the query and give the correct answer in order to win. It shows a form of word productivity by children. The tone of the game is that of the tongue twisterslai lai, kpai kpai’. These words have some form of cultural meaning. For the purpose of this game,is an affirmation, while ‘lai lai and kpai kpai’ are used to refute the queries. Other cultures will use different responses for the expression of this same game.Therefore the language of the game is culture specific. Other cultures may use something other than flying objects and mammals. The choice of what constitutes the components or the contents of this game depends on the cultural background of the people.

4.2.1 Mathematics concepts in the game

The technique in playing this game involves the identification of numbers. When an object with two legs is mentioned, the participants should know that it can fly, but if the object has four legs, they should know that it cannot fly. If a player misses the calculation,he is fired. On the other hand, an animal that has two legs does not carry pregnancy and as such cannot give birth. Two-legged objects belong to the family of birds and can lay eggs,while four-legged animals give birth.

The game is played by using number facts. Numbers that sum up to four are ‘no’,while two is a ‘yes’ for flying objects. The reverse form is used for perfection in number identification in mammals. At the same time, the leader is made to mention up to eight,ten, or twelve names of animals. The process of itemization of animals in the pairs of 2:4 legs is used for the identification of animals in a particular group. Using number facts makes the rhyme to be very exciting and brain stimulating as the children verbalise their calculation in order to win. The leader also applies number skills to mix up the list of the tokens used in order to beat other participants.

4.3 Game 3.

This is a form of guessing game. It involves the pairing of players. The two players stand facing each other, with a pebble in the palm of only one of the pairs. The player with the pebble starts the game, by moving his hands backward. At that point, he moves the pebble from one hand to another, while chanting the rhyme in example 4.

The leader continues moving the pebble from one hand to the other. When he is convinced that the pebble is hidden from his opponent, he folds his fingers into a fist to conceal the pebble from being easily sighted and stretches his hands for the opponent to make a guess. This action is taken in order to confuse the partners, by not letting them know in which fist the pebble is hidden. When the partner makes a guess by touching the fist, the leader opens his fist with a smile to show excitement.

If the guess is correct, this is counted as a point, but if it is wrong, the point is given to the leader as a bonus. The player continues to hide the pebble until the partner has a correct guess before s/he takes over. At the end, the scores are added and a winner is declared based on the aggregate.

4.3.1 Mathematics strategy

The strategy involved in the game is a form of guessed identification. Only one pebble is used. The pebble is hidden in one of the fisted hands. A correct guess earns a score of 1 point, while a wrong guess attracts zero. The game is repeated several times for an accumulated score. The game is therefore used for the learning of probability and addition. The probability shows the number of total rounds played and the number of rounds led by each player, compared to the total number of rounds. The leader cannot hand over the role to the next player until s/he makes a correct guess.

This is illustrated on a table as shown:

Table 1. A representation of the activities in the game

Table 1. A representation of the activities in the game

Rounds Leading Guessing Hidden pebble Guess Scores Guessing points Ime Ini 1 Ime Ini Left Left 0 1 Correct 2 Ini Ime Left Right 0 1 Correct 3 Ini Ime Right Right 1 0 Wrong 4 Ime Ini Left Left 0 1 Correct 5 Ini Ime Right Right 1 0 Wrong 6 Ime Ini Right Left 0 1 Correct 7 Ime Ini Left Left 0 1 Correct 8 Ini Ime Left Left 1 0 Wrong 9 Ime Ini Left Right 1 0 Wrong 10 Ime Ini Right Left 1 0 Wrong 11 Ini Ime Right Left 0 1 Correct 12 Ini Ime Left Right 0 1 Correct Rounds 12 Ime=6 rounds Ini=4 Ini=6 guesses Ime=4 5 points 7 points

The calculation involves:

How many rounds was the game played?

How many times did each person lead?

How many rounds did each player guess?

How many times did each player guess correctly?

How many times did each player guess wrongly?

What is the probability of guessing to leading for each player?

What is the total points for each player compared to each round of guessing?

The recording and calculation processes are very vital for the learning of mathematics.The children should be able to record numbers (scores), and calculate the total rounds,and total numbers of guesses/rounds leading for each person compared to the total scores. This could be highly exciting when they can recall the rounds, and number of guesses vs rounds leading. Therefore, the game has positive implications for number facts, subtraction, and addition. The final processes of total scores for guessing/leading compared to the numbers of rounds requires the mathematics processes of addition,subtraction, and division.

4.4 Game 4.(Airborne pebble game)

The game involves a careful and calculated picking up of pebbles while avoiding the interaction of the pebble(s) with any other pebble on the floor. Seven pebbles are selected,one serving as the air-borne pebble while other six being focused on and picked up. These processes take seven rounds for a winning point.

The game is played by a minimum of two persons. If the participants are more than two, the turns in playing rotates in an anti-clockwise direction. The first player collects the seven pebbles, throws them on the floor, selects the airborne pebble and picks up the pebbles on the floor as follows:

1. Pick up only one pebble at a time and use it to catch the airborne pebble, without allowing it to land on the floor. Put that particular pebble aside and pick up another one, using the same format. Continue picking up the pebbles in that order until s/he complete the picking up process without any left over.

If the pebble or the finger(s) of the player interacts with any other pebble on the floor,and if the player does not catch the airborne pebble properly in each round, the player has committed a foul and is the next player’s turn. If the player succeeds at this stage, he moves into the second round.

2. Using the same throwing process in (1), pick up two pebbles and use them to catch the selected airborne pebble. Put the two pebbles aside, continue picking up another set of two pebbles, until s/he completes the picking up process in that round, following the rules in round one. If the player commits a foul, the player to his right takes the next turn. On the other hand, the player moves to round three if s/he does not violate any rule.

3. Throw the seven pebbles on the floor, select the airborne pebble and throw it upward. Pick up three pebbles and use them to catch the airborne pebble. Put the three pebbles aside and pick up the remaining three, using the same format. If the player succeeds, he moves to round four.

4. At this point, the picking up process involves four pebbles. Put the four pebbles aside and pick up the remaining two.

5. Pick up five pebbles to catch the airborne pebble, and then pick up the remaining one pebble. If the player does not commit any foul, s/he moves to round six.

6. Throw the seven pebbles on the floor. Then, select the airborne pebble. When the airborne pebble is selected, six pebbles are left. Throw the airborne pebble into the air, catch it while picking up the six pebbles without allowing any to drop out. Round six is played once, since there are no other pebbles on the floor after picking up the six.

7. The seventh round is the final, and the scoring level. The processes in this round are different from that in rounds one to six. The (seven) pebbles all serve as the airborne pebbles. Two hands are used to catch the airborne pebbles. The throwing is done with one palm, while the back of the two hands are used in catching the pebbles.

8. Throw the seven airborne pebbles into the air and catch them all at once, using the back of the hands rather than the palms. This is done by interlocking the thumbs to join the two hands, after throwing the pebbles into the air. If any of the pebbles falls on the floor, it is counted as a foul against the player. The game at that point moves to the next player. On the other hand, upon the completion of the final round by the successful player s/he gets seven points and still hands over to the next player.

The completion of all the stages earns seven points. A foul committed at any stage earns zero points. This means that even if the foul is committed at the first or final round, the player’s score is zero. The score is seven points multiplied by the number of completed successful turns. The candidate with the highest score is declared the champion of the game. The process is presented in Table 2.

Table 2. Rounds and selection process in

Table 2. Rounds and selection process in

1. Rounds 2. Airborne pebble 3. Number of pebbles selected at each round 4. Pebbles gathered at each selection 5. Selection methods used 1 1 1:1:1:1:1:1 2:2:2:2:2:2 7-1/1=6 2 1 2:2:2 3:3:3 7-1/2=3 3 1 3:3 4:4 7-1/3=2 4 1 4:2 5:2 7-1/4=4.2 5 1 5:1 6:2 7-1/5=5.1 6 1 6. 0 7 7-1/6=1 7 1 7.0 7 7-0=7

In each round, the number of pebbles selected is presented in column 2. This is added to the airborne pebble in column 3 to get the total catch as shown in column 4. The selected pebble(s) are dropped, while the airborne pebble continues to be added to each selection (column 4) in each round.

This game is used for the development of a child’s sense of focus, concentration,and action. It involves an interaction with the earth, space, and time. The player has to calculate the space and speed of the airborne pebble and measure it with the time spent in separating the pebbles on the floor and the time involved in catching the airborne pebble.

4.4.1 Mathematics concepts in the game

The game is used for the learning of counting, subtraction, simple proportions, division,and addition. The whole number is seven.

? The first stage involves the subtraction of one (i.e. the airborne) pebble from seven. The answer is six (7-1=6).

? The second stage involves division. The remaining six pebbles are divided into six, and each person has one pebble. The sharing method moves from one to two in stage two, three in stage three, and increases in that order until the final stage which involves seven numbers.

? The airborne pebble remains as a constant number that is added to each selection, which marks the difference between the numbers in columns 3 and 4. At the final stage, all the pebbles are used for the airborne pebble and the player must catch all at the same time,using the butt of palms.

? The game of multiplication is at the result stage. As observed earlier, the completion of the final stage/round attracts seven points. The score of the optimal candidate is calculated by the multiplication of seven by the number of successfully completed rounds.

The game is therefore useful in the teaching of the multiplication of seven, division of six, ratios, LCM, fractions, subtraction, and addition.

The children have fun in throwing the airborne pebble into the air and catching it after picking the selected pebbles up from the floor. The sound produced when the airborne pebble interacts with the selected pebbles is exciting, too. The game demands a high level of concentration in order to separate and pick up the correct numbers in each round,while timing the movement of the airborne pebble all at the same time. Mathematics requires full attention from the students for quick understanding. Therefore, the attention given in this game could be applied to the learning of mathematics in a formal setting.Number facts are important aspects of this game, which is the first stage in the learning of mathematics.

The number ‘seven’ is highly significant in Anaang culture. It represents completeness. This explains why the final round involves the use of the seven pebbles without any subtraction, to show the completeness of the game. The butt of the palm is used for catching these pebbles to express the belief that after seven rounds of rebirth,you turn your back and bid the earth a final goodbye, since you have completed your life circle.

4.5 Game 5. Nsa ikpe (Pebble-catching game)

This is a game of guessing and calculation. The contents of the game comprise fortyeight pebbles and twelve circles designed in six columns and two rows. The circles could be carved in wood for mobility or bored into the sand using a spherical stone. Each hole contains four marbles. This is illustrated in Table 3.

Table 3. A diagrammatic representation of

Table 3. A diagrammatic representation of

?

Two players are involved at a time. Others sit and watch, while waiting for their turn and taking over when one of the partners loses. The two players face each other.

A coin is tossed to kick-start the game. The game requires a careful calculation of where to start in order to emerge the winner.

The laws of the game are as outlined:

? There must be four seeds in each circle.

? The first person can take the four seeds from any circle.

? Release only one seed at a time into the following circles in an anti-clockwise manner.

? Continue until the last seed is released.

? The seed must end in an empty pit/circle.

? The winning position is four seeds on either side of the rows.

? If the last seed is dropped into a circle that is not empty, continue to remove all and keep on filling other circles by dropping only one seed at a time until the last seed falls into an empty circle.

If the player drops the last seed into a circle that has an existing three seeds, the player simply collects the four seeds from that circle as a bonus and pauses for the partner to take over. At the same time, if the last seed is dropped into an empty pit, the second partner takes over. The game continues in that order and the two partners continue to win by taking the seeds from their rows when a pit has up to four seeds. The game ends when both partners have no seed in their circles or when there are only four seeds remaining with only one of the partners.

As the player drops the seeds, each partner gets a point if there are up to four seeds in any of the circles on his row. He can also get a bonus point from the side of his partner if his last seed lands in any circle other than his own. In the process of filling, if any circle has up to four seeds/pebbles, the partner that is assigned to that row claims it. The first round ends when all the circles are empty.

Each player refills the circles on his rows with the winning seeds. Scores are calculated per circle. If the partner does not have enough seeds to refill his row, it means the empty circle(s) are ceded to his opponent. In other words, if a partner has an empty circle, it means the opponent has an added advantage over him, takes over the empty pit,and demarcates it. The winner will have to break into the side of his partner and claim those circles. The game continues until the opponent reclaims his circles or continues to give way until he has only four seeds, which is equivalent to one out of the six circles(1/6). The partner with more seeds/circles is declared the winner.

4.5.1 Using the game for the learning of mathematics

The game has much to do with calculation, number facts, multiplication, subtraction, and addition.

? The total number of seeds used = four multiplied by the twelve circles for a total of fortyeight (4x12=48).

? The seeds are further divided into two rows for a total of twenty-four (48/2=24).

? The next stage is filling the six circles on your row with four seeds each. This involves dividing twenty-four by four (24/4=6).

? The process of filling the circle involves an additional process of counting to ensure that each pit has four and only four seeds.

? The next stage is the actual playing of the game.

? It requires careful calculation of the terminal point in order to know where to begin. If a partner knows the number of seeds in his target pit and where the last seed will fall, he is likely to have higher chances of beating his opponent.

? The total number of seeds used is forty eight. The children could use this for counting from one to forty-eight.

? The number of circles is twelve.

? The circles are further divided into two (12/2=6). This is a clear example of division.Therefore, the LCM of the numbers 48, and, 24 could be 12, 6, 4, 2, 1. The number facts here are derived as follows:

? 48=total number of seeds

? 24=seeds in each row

? 12=total number of circles

? 6=number of circles in each row

? 4=number of seeds in each circle/wining number

? 2=two rows/ two players

? 1=movement of the seeds at a time

It is easy for children to use this game in calculating these numbers and use them for the learning of LCM, division, multiplication, subtraction, factorization, ratios and even fractions.

The game involves brain drills, calculations, and fast reasoning. The player has to calculate his starting point prior to his finishing point. He will do a kind of mental calculation of the number of pebbles in a circle, and also calculate the number of moves and the terminal point in each round. He has set goals which determine the expected outcome as he drops the pebbles. This guides him to preempt his total target catch. The calculation process following Gerdes (2014) and, Azuka and Adeyemi (2012) is a higher level of mathematics thinking.

4.6 Game 6. (Pebble-picking game)

This play is more of a logical calculation game, which requires the wisdom and the attention of the player for success. The game is played in a group of three partners or more.

The contents are made up of the player and the pebbles/gravel/seeds.

The player is called the father while the seeds are the soldiers and messengers.

It is a narrative, and also participatory game:

The father has gathered his children at home to narrate an ordeal with his messengers in his palace. He had twelve workers/soldiers and three messengers. He sent two of his workers on an errand, but the three messengers volunteered to go. Later the messengers came back with no positive result.

He then sent another two workers out, the same three messengers volunteered to do the job, but returned to tell the master that they did not see anything.

The master continued sending additional pairs of workers out and the messengers continued volunteering and returning with disappointing messages, until the master sent the last batch. The three messengers volunteered as usual and also returned without accomplishing the mission. The illustration is presented in Table 4 below.

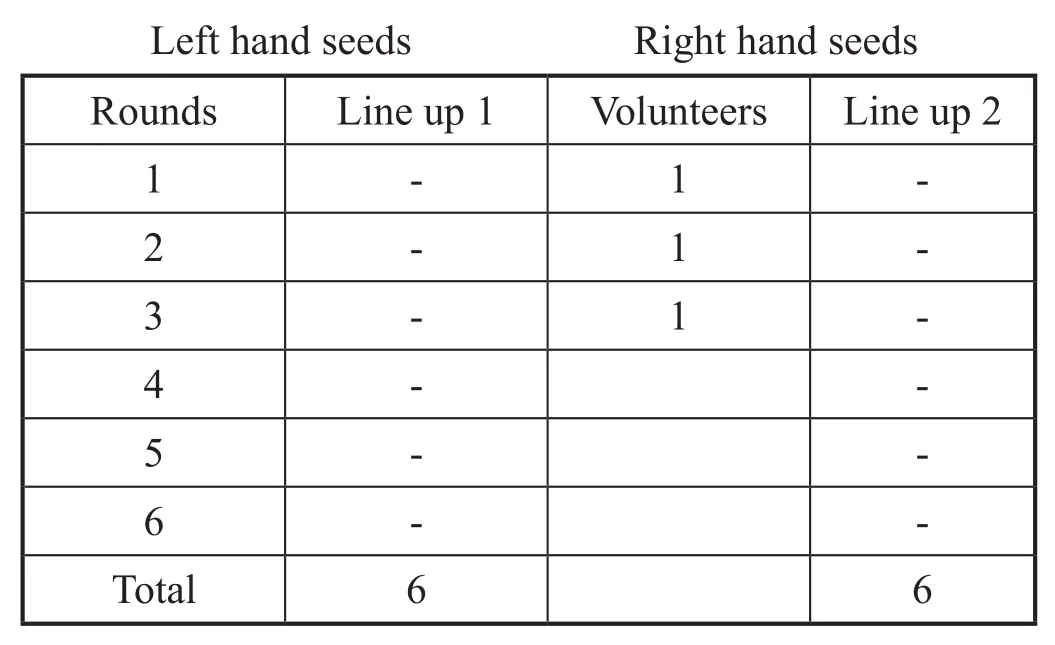
Table 4. An illustration of the rounds and the volunteers that later returned

The ‘dashes’ are used to show that the workers did not come back, while (1) in the centre column shows that the volunteers actually returned.

? The seeds in the first column are picked up with the left hand, those in the third column are picked up with the right hand.

? Round 1 represents the first set of workers for the errand.

? The three central seeds are picked up one after the other, using the left, right, then left hand,to show their exit. The three messengers came back with negative report. This is indicated by dropping back the central seeds one by one, starting from the right hand, the left, and then the right again.

? The main workers did not come back as indicated with the ‘-’ so he moves to round two and send out another pair of workers. In the process of sending, he picks up another pair of seeds in the same format.

? The same batch of messengers volunteers. This is indicated with the picking up of the middle seeds. They all come back with failures. Then he moves to the next round.

? The same method of picking is used to tell the story until the last round; when the three messengers came back with failure as usual, the three central seeds are dropped to show their return.

? All the seeds picked up are hidden in the leader’s fist.

The participatory aspect goes this way:

The father is the leading player and the narrator at the same time.

The children are all the other players.

The soldiers are the twelve seeds, arranged in two vertical lines.

The messengers are the three seeds arranged in the centre column.

The first three seeds have three columns, others are arranged in two columns.

The game involves the picking up of all the seeds one by one, using both hands simultaneously.

The leader picks two seeds (the soldiers), one with the left and the other with the right hand, and chants ‘I sent these two soldiers on an errand’.

The next stage involves pointing at the three central seeds, and picking them up one after the other, chanting, ‘this one said I shall go, this one said I shall go, this one said I shall go’.

Picking the seeds up one by one with the right, left, and then right hand, he continues with his chants.

The third stage is the dropping of the central seeds one after the other, starting with the left hand, right, then left, he continues chanting, ‘this one said I have not seen it, this one said I have not seen it, this one said I have not seen it’.

The chanting, picking up, and the dropping continue until all the seeds are picked up and the three seeds dropped at the final stage to show their failure. In the end, he folds his hands into fists letting the children to guess the number of seeds in each. If the guess is correct, it is counted for that person as a point and the partner takes over as the father.Even if his guess is wrong, and he is declared a loser, the loser takes over from the leader.

The leader is expected to have only one seed in his left hand and eleven seeds in his right. If this number does not tally with what he has, then the leader can not win.

4.6.1 Mathematics ideas in the game

The game first involves counting from one to fifteen, subtraction of three from fifteen,and division of twelve into two.

The centre seeds are added and used for the learning of fractions and calculations.

The picking up and dropping are used for the calculation of ratios.

The calculation involves dividing fifteen by two, and subtraction of three.

The picking up and dropping method is used for addition, subtraction, and fractional calculation.

The idea of arranging the seeds in rows and columns is relevant in the learning of the representation of numbers on a table. Logical calculation is needed in the picking up and dropping stages in order to arrive at a correct number of seeds in each palm. The result is 1:11, whereas the number of moves is the same for both hands. The player should determine the hand that should move first at each round and the hand that should first drop the returning messengers. This requires learning the rules of the game, which plays a vital role in mathematics. Mathematics involves step by step calculation before arriving at the result, which is the final answer. If there is a mix-up along the way, the answer will be wrong. Using this game therefore exposes children to logical calculation in order to get the correct answer.

5. Discussion and Conclusion

The selected games are not exclusively Anaang based, they cut across other African culture. The only difference is just in the name. For instance, the game ‘nsa ikpe’ is called‘a(chǎn)yo’ in Yoruba, ‘okwe’ in Igbo, ‘wari’ in Senegal and ‘mancala’ in Arabic. This portrays the existence of the basis of universal activities in all cultures.

The games have fixed sets of rules, but the goals and scoring points vary from culture to culture. For instance, Ghana uses five pebbles in airborne pebble game (Mereku &Mereku, 2014), while Anaang uses seven. All the games in this research deal with the classification and solution of mathematics problems posed by the games and explore the possibilities of transmitting the ideas in these games to the learning of mathematics.

There are several moves used in each of the selected games, but the benchmark of the moves is specific to each game. The moves determine the scoring points and overall results of the game. Based on this, each player develops hidden skills/tactics for his success. The skills involve rethinking of mathematical ideas involved in the game,and a mastering of how to apply these ideas effectively. For instance, the game ‘pebble messengers’ requires logical calculation of the first and second moves in each round in order to have just one pebble in one hand and eleven in the other hand.

The core activities in the selected games evolve around mathematical ideas such as number facts, fractions and calculations. The contents of the games also involve mathematics icons like counting sticks, pebbles, and circles. At the onset of the game,the pebbles/sticks are first counted to certify the required number of tokens used. The numbers vary according to the type of games involved. The numbers in the selected games include: 1 for (mkpainuun),, 48 (nsa ikpe),however, the game ‘-tinka’ makes use of concepts rather than concrete objects. This is in line with the fact that mathematics games are used for the consolidation of mathematics concepts (Mereku & Mereku, 2014).

The relationship between visual memory and concentration are the main factors for success in African games. The spirit of concentration is also the key to success in mathematics. If children are exposed to the mathematics ideas involved in the games at their early stage, it is possible for them to transfer the interest acquired in the playing of game to the concentration required in mathematics. This will help deleting the feelings of boredom in the mental activities of mathematics by children.

The set rules of the game constitute the basis of theoretical approach in the selected mathematics games. The rules marry mathematics concepts with cultural ideas, leading to the adoption of an interdisciplinary theoretical approach for the crossing of the bridge between sciences (mathematics) and humanities (games) disciplines. This, therefore shows the survival of a mental interaction of culture with mathematics.

In conclusion, there is a high level of interaction between African languages and mathematics learning which relates relevant ideas of culture to mathematics-related concepts. Despite the relevance of games to the study of mathematics, the awakening interest by scholars to develop African mathematics-related games for indoor activities is very weak compared with the interest toward developing games from Western cultures.At the same time, there exist few texts on African mathematics games in general and Nigerian games in particular, and texts on games from Anaang are non-existant.

Mathematics games deal with the classification and solution of mathematics problems and explore the possibilities of using these solutions for success in the games. Therefore,mathematics does not exist in isolation; it is tightly connected with culture. For instance,the principles of mathematics involve calculation of all forms, and the application of these calculations for the solution of problems in society including gains and losses in business culture. We therefore posit that aspects of African traditional mathematics, which are embedded in diverse indigenous games, should be developed to trigger more interests in mathematics, and formal indoor and outdoor activities, both for the preservation of culture and to save the rich African as well as Anaang heritage from cultural suicide.

Adenegan, K. E., & Adedoye, A. Z. (2017). Mathematical games development, effects and application on teaching and learning mathematics. A case study of some selected schools in Ondo West Local Government Area, Ondo State, Nigeria.Science and Technology, 3,70-84.

Amstrong, R. G., & Bamgbose, A. (1971).Mathematical concepts in Yoruba. A manual of Yoruba teachers.Ibadan: University Press.

Ascher, M. (1990). A river-crossing problem in cross-cultural perspective.Mathematics Magazine,63, 26-29.

Ascher, M. (1991).Ethnomathematics: A multicultural view of mathematics ideas. Pacific Grove:Brooks/Cole.

Ascher, M., & Ascher, R. (1981).Code of the Quipu: A study in media, mathematics and culture.Ann Arbor: The University of Michigan Press.

Azuka, F., & Adeyeye, A. (2012). Developing and use of mathematical games.Mathematical Theory and Modeling, 2(8),10-16.

Bishop, A. (1988).Mathematical enculturation, a cultural perspective on mathematics education.Doedrechet: Kluwer.

Bohannan, P. (1953). Concepts of time among the Tiv of Nigeria. South Western Journal of Anthropology, 9,251-263.

Booth, N. (1975). Time and change in African traditional thought.Journal of Religion in Africa,7(2), 81-91.

Campbell, P. (1977). An experimental course of African mathematics.Historia Mathematica, 3,467-478.

Carraher, T. (1988). Street mathematics and school mathematics.Proceedings of the 12th International Conference of Psychology of Mathematics Education, 1-23.

Crowe, D. (1975). The geometry of African art 11, A catalogue of Benin patterns.Historica Mathematica, 2, 253-277.

Crowe, D. (1982). Symmetry of African art.Ba Shiru Journal of African Languages & Literature,3,57-71.

D’Ambrosio, U. (1977). Mathematica e sociedade.Scie^ncia e Cultura, 28,1418-1422.

D’Ambrosio, U. (1982).Mathematics for rich and poor countries. Paramaribo: Carimath.

D’Ambrosio, U. (1984).The intercultural transmission of mathematical knowledge: Effects on mathematics education. Campinas: Unicamp.

D’Ambrosio, U. (1985).Socio-cultural basis for mathematics education.Campinas: Unicamp.

Davis, E., Bishop, A. J., & Tiong Seah, W. (2008). Gaps between inside school and out-of-school mathematics in Ghana.Mathematics Connection, 8, 1-15.

Doregowski, J. (1972). The role of symmetry in pattern production by Zambian children. Journal of Cross Cultural Psychology, 3(3), 303-317.

Etuk, E. (1967). The development of number concepts. An examination of Piaget’s theory with Yoruba Nigerian children.Columbian teachers college manual.

Ferdig, R. (2009).Learning and teaching with electronic games. Chasapeake, VA: Association for the Advancement of Computing in Education.

Finnegan, R. (2012).Oral literature in Africa. United Kingdom: Open Book Publishers.

Gay, J., & Cole, M. (1967). The new mathematics and the old culture: A study of learning among the Kpelle of Liberia.NY: Holt, Rinehart & Winston.

Gerdes, P. (1984).Ethnomathematics: A new research field, illustrated by studies of mathematical ideas in African history.Aramaribo: Carimath.

Gerdes, P. (1985). Conditions and strategies for emancipatory mathematics education in undeveloped countries.For the Learning of Mathematics, 5(3),10-17.

Gerdes, P. (1986). How to recognize hidden geometrical thinking: A contribution to the development of anthropological mathematics.For the Learning of Mathematics, 6,10-17.

Gerdes, P. (1989). Reconstruction on the extension of lost symmetric: Examples from the Tamil of South India.Computers and Mathematics With Applications,17(2), 45-59.

Gerdes, P. (1990). On the mathematical elements in the Tchokwe drawing tradition: Discovery and innovation.Journal of African Academy of Sciences, 3,29-36.

Gerdes, P. (1994). On mathematics in the history of Sub-Saharan Africa.Historia Mathematica,21,345-376.

Gerdes, P. (2000).Culture and the awakening of geometrical thinking: Anthropological, historical and philosophical considerations. An ethnomathematical study.Minneapolis: MEP Press.

Gerdes, P. (2014).Mathematics education in Mozambique. Papers in the early 1980s.Mozambique: ISTEG-University Boane.

Habibu, B. (2005).Ethnomathematics. The case of mallam Na Barkin kogi. Nigeria: BUK Press.

Hoffman, M. H. (2006). What is a ‘semiotic perspective’, and what could it be? Some comments on the contributions to this special issue.Educational Studies in Mathematics,61, 279-291.

James, R. (1982). How students can own mathematics.Journal of Ethnomathematics,5, 23-40.

Kani, E. A. (1992). Arithmetic in the pre-colonial central Sudan. In G. Thomas-Emeagwali (Ed.),Science and technology in African history with case studies from Nigeria, Sierra Leone,Zimbabwe, and Zambia(pp. 33-39). Lewiston: Edwin Mellin Press.

Mereku, C. W. K. (2012).Wesing and learn: A legacy of songs for Ghanaian schools.Winneba:University of Education, Winneba.

Mereku, D., & Mereku, C. (2014). Ghanaian case study of singing games in ethnomathematics.Journal of African Culture and International Understanding, 6,16-24.

Michael, I. (2013). A socio-phonological description of Anaang proverb-riddles.JLL, 4(2), 77-89.

Mohammed, W. Y., Ibrahim, S., & Hathiru, A. (2010). Ethnomathematics (A mathematics game in Hausa culture).International Journal of Mathematical Science Education, 3,36-42.

Musa, M. (1987).The mathematics heritage of the Hausa people: A resource guide for mathematics teaching.Zaria: ABU.

Orey, D. C., & Rosa, M. (2006). Ethnomathematics: Cultural assertions and challenges towards pedagogical action.The Journal of Mathematics and Culture,1, 57-78.

Otte, M. (2003). Mathematic, Zeichen und takigkeit. In M. Hoffman (Ed.),Mathematik verstchen:semiotische perspektiven(pp. 206-241). Franzbecker: Hildescheneim.

Prince, A., & Smolensky, P. (1993).Optimality theory: Constraint interaction in generative grammar. Boulder: Rutgers University and University of Colorado.

Stephen, P., & Carry, S. (1994). Designing and evaluating games for teaching science and mathematics: An illustration from coordinate geometry.Summer Education,16(3), 37-50.

Sumbabi, U. T., & Bassey, U. E. (2013). Mathematical games and simulation on senior secondary school student’s interest in geometry.JORIND, 11(2),330-344.

Zaslavsky, C. (1998). Ethnomathematics and multicultural mathematics education. Teaching Children Mathematics, 4(9), 502-513.

Zhang, W., & Zhang, Q. (2010). Ethnomathematics and its integration within the mathematics curriculum.Journalof Mathematics Education, 3(1), 151-157.