Singular Solutions to Conformal Hessian Equations
Nikolai NADIRASHVILI Serge
(Dedicated to Professor Haim Brezis on the occasion of his 70th birthday)
1 Introduction
In this paper,we study a class of fully nonlinear second-order elliptic equations of the form

defined in a domain of Rn.Here D2u denotes the Hessian of the function u,with Du being its gradient.We assume that F is a Lipschitz function defined on a domain in the space Sym2(Rn)×Rn×R,with Sym2(Rn)being the space of n×n symmetric matrices,and that F satisfies the uniform ellipticity condition,i.e.,there exists a constant C=C(F)≥1(called an ellipticity constant),such that

for any non-negative definite symmetric matrix N.Ifthen this condition is equivalent to

Here,uijdenotes the partial derivative
ijA function u is called a classical solution to(1.1)if u ∈ C2(?)and u satisfies(1.1).Actually,any classical solution to(1.1)is a smooth Cα+1-solution,provided that F is a smooth Cαfunction of its arguments.
More precisely,we are interested in conformal Hessian equations(see,e.g.,[9,pp.5–6]),i.e.,those of the form

with f being a function on Rninvariant under permutations of the coordinates,and

being the eigenvalues of the conformal Hessian in Rn:

where n≥3,u>0.In fact,in our setting the functionψ(u,x)is identically 0.
If F has this form,it is invariant under conformal mappings,i.e.,transformations which preserve angles between curves.In contrast to the case n=2,for n≥3,any conformal transformation of Rnis decomposed into a finitely many family of M?bius transformations,that is,mappings of the form

with x,z∈Rn,k∈R,a∈{0,2}and an orthogonal matrix A.In other words,each T is a composition of a translation,a homothety,a rotation and(may be)an inversion.If T is a conformal mapping and,where JTdenotes the Jacobian determinant of T,then F[v]=F[u].
We are interested in the Dirichlet problem

where??Rnis a bounded domain with a smooth boundary??andφis a continuous function on ??.
Consider the problem of existence and regularity of solutions to the Dirichlet problem(1.4)which has always a unique viscosity(weak)solution for fully nonlinear elliptic equations.The viscosity solutions satisfy the equation(1.1)in a weak sense,and the best known interior regularity(see[1–2,8])for them is C1+εfor some ε >0.For more details,see[2–3].Recall that in[4],the authors constructed a homogeneous singular viscosity solution in 5 dimensions for Hessian equations of orderδfor anyδ∈]1,2],that is,of any order compatible with the mentioned interior regularity results.In fact,we proved in[4]the following result.
Theorem 1.1The function

is a viscosity solution to a uniformly elliptic Hessian equation F(D2w)=0 with a smooth functional F in a unit ball B?R5for the isoparametric Cartan cubic form

with
It proves the optimality of the interior C1+ε-regularity of viscosity solutions to fully nonlinear equations in 5 and more dimensions.
In this paper,we show that the same singularity result remains true for conformal Hessian equations.
Theorem 1.2Letδ=1+ε∈]1,2[,ε∈]0,1[.The function
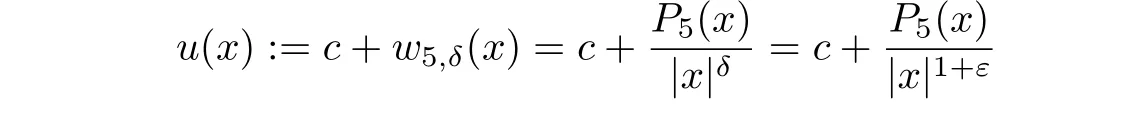
is a viscosity solution to a uniformly elliptic conformal Hessian equation(1.1)in a unit ball B?R5for a sufficiently large positive constant c(c=106is sufficient for
The idea behind this choice of u(x)is that the conformal Hessian of u has the form cD2w plus a term which does not depend on c,that is,the conformal Hessian is(relatively)very close to cD2w for large enough c>0 which permits to use a very precise information on the spectrum of cD2u obtained in a previous paper(see[4]).
Notice also that the result does not hold forδ=1,and we do not know how to construct a non-classical C1,1-solution to a uniformly elliptic conformal Hessian equation.
The rest of the paper is organized as follows.In Section 2,we recall some necessary preliminary results,and we prove our main result in Section 3.To simplify the notation,we suppose thatin Section 3.For anyδ,the proof is along the same line,but more cumbersome.However,we give also some indications for a generalδ.In fact,all proofs but one(Lemma 3.4 which is more cumbersome)remain valid for any δ∈]1,2[.In our proofs of Sections 2–3,we used MAPLE to verify some algebraic identities.However,these calculations of derivatives and eigenvalues do not exceed human capacities and could be verified by a hardworking reader.
2 Preliminary Results
Notation 2.1For a real symmetric matrix A,we denote by|A|the maximum absolute value of its eigenvalues.
Let u be a strictly positive function onDefine the map

where λ(S)={λi:λ1≥ ···≥ λn} ∈ Rnis the ordered set of eigenvalues of the conformal Hessian

Denote Σnthe permutation group of{1,···,n}.For any σ ∈ Σn,we denote by Tσthe linear transformation of Rngiven by
Let a,b∈ B1and letμ1(a,b)≥ ···≥ μn(a,b)be the eigenvalues of the difference Au(a)?Au(b).The following ellipticity criterion can be proved similarly to Lemma 2.1 of[5].However,note that in the present setting,one needs the positivity of u which we suppose everywhere below.
Lemma 2.1Suppose that the family


is uniformly hyperbolic,i.e.,if{μ1(a,b,O) ≥ ···≥ μn(a,b,O)}is the ordered spectrum of M(a,b,O)0,then for some constant C>1.Then w is a viscosity solution in B1to a uniformly elliptic conformal Hessian equation(1).
We recall then some properties of the function,and of its Hessian D2w proved in[4].
Lemma 2.2There exists a 3-dimensional Lie subgroup GPof SO(5),such that P is invarant under its natural action and the orbitof the circle

under this action is the whole
This result permits to parametrize the values of w5,δ(x)and the spectrum Specby a single number p∈ [0,1],where x lies in the orbit of
Lemma 2.3.(i)Letand let x∈GP(p,0,0,r,0)with p2+r2=1.
Then2and

for

where

(ii)Letλ1≥ λ2≥ ···≥ λ5be the ordered eigenvalues of D2w5,δ(x).Then
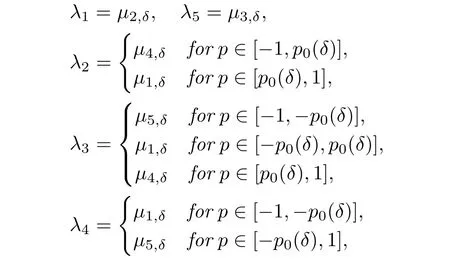
where

Remark 2.1Notice the oddness property of the spectrum:

Proposition 2.1LetSuppose thatand let O∈O(5)be an orthogonal matrix s.t.

DenoteΛ1≥ Λ2≥ ···≥ Λ5the eigenvalues of the matrix Nδ(a,b,O).Then

forone can choose C=1000.
As an immediate consequence we get the following result.
Corollary 2.1In the notation of Proposition 2.1 we have

We need also the following classical Hermann Weyl’s result.
Lemma 2.4Let AB be two real symmetric n×n matrices with the eigenvaluesrespectively.Then for the eigenvalues Λ1≥ Λ2≥ ···≥ Λnof the matrix A?B,we have

3 Proofs
Let n=5,u(x)=c+w5,δ(x).We begin with δ=1 and show that the result is false in this case.Indeed,letThen
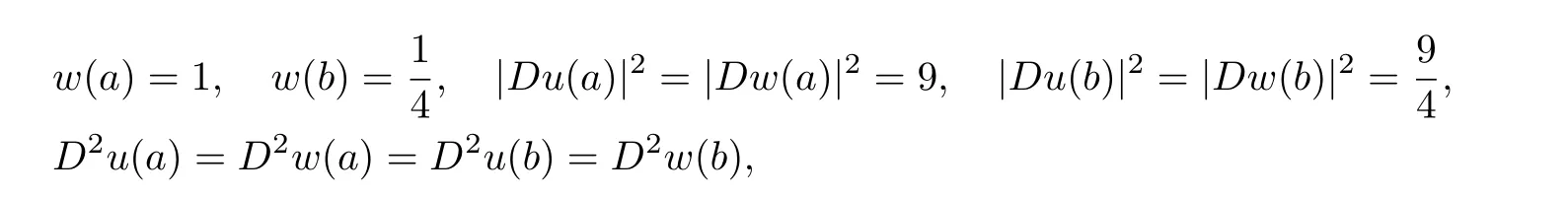
and

which is negative since the spectrum of D2w(a)is(2,2,2,?7,?7).The reason is clearly that D2w(a)forδ=1 is homogeneous order 0 and does not depend on|a|.
Remark 3.1More generally,the same argument applied to the points

for small enoughλ>0 shows that a solution of the form c+v for a constant c and an order 2 homogeneous function v is impossible for a conformal Hessian equation.
Suppose now thatδ∈]1,2[.We formulate below the results which we need to prove the main theorem for anyδ∈]1,2[,but give detailed proofs only for(and c=106).However,we point out how to modify the arguments for a generalδ∈]1,2[.First we spell out Lemma 2.3 for
Lemma 3.1(i)Let,and let x∈GP(p,0,0,r,0)with p2+r2=1.Then

for

(ii)Letλ1≥ λ2≥ ···≥ λ5be the ordered eigenvalues of Spec(D2u(x))=Spec(D2w(x)).Then

where

We will need also the derivatives of the eigenvalues.
Lemma 3.2 LetThen


For the generalδ∈]1,2[,we give only the two most complicated derivatives:
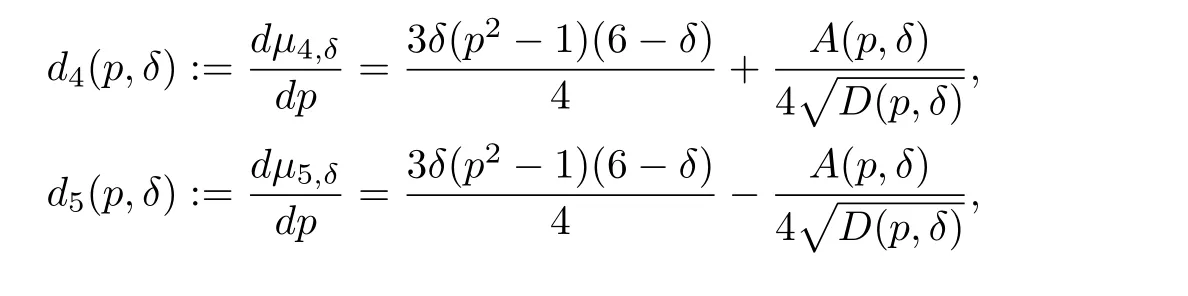
where

and D(p,δ)is defined in Lemma 2.3.
Simple calculus gives the following result.
Corollary 3.1Define

Then

for an absolute constant d>0(one can take d=100).For,one has

Below we denotethe relation of Di(p)and di(p)is clear from Lemma 3.1(ii);for example,D1(p)=d2(p),D5(p)=d3(p).
The proof of Theorem 1.2 is based on some auxiliary lemmas which use the following notation.Let us take two points

and letBelow we use the following quantity K depending on the pair(a,b):

and work with the following matrices depending on(a,b)and on an orthogonal matrix O(and also onδ):

Lemma 3.3There holds

with C1(δ)=c1(2? δ)for an absolute constant c1.Forwe can take
ProofNotice first that|Du(a)|2=|Dw(a)|2,|Du(b)|2=|Dw(b)|2.Since P=P5(x)can be represented as the generic traceless norm in the Jordan algebra Sym3(R),it verifies the eiconal equation|DP(x)|2=9|x|4(see,e.g.,[7]).Then letAn easy calculation gives

sinceThus

Same calculation gives for the generalδ,

Repeating the argument,we obtain the conclusion.
Lemma 3.4Let.Then

for a positive constant C2(δ)depending only on δ.Forcan take
ProofIf one replaces a byand b bythe quantity M gets bigger and K gets smaller.Therefore,we can suppose that|a|=s=1.Then we have

By Lemma 2.4,we have

Let thenSuppose first p≥q.Ifthen

(by a simple calculation using the explicit formulas for D1,λ1).Therefore,

If q

Then suppose that q

and thus

which finishes the proof for p≥q.The case q≥p is treated similarly(replaceλ1byλ5andλ2byλ4).
For the generalδ∈]1,2[,the argument is similar,but more cumbersome.It shows that we can take C2(δ)=c2(2 ? δ)2for an absolute constant c2>0(say,c2=0.001).
Remark 3.2Notice that Lemma 3.4 is false forδ=1.
Lemma 3.5Let
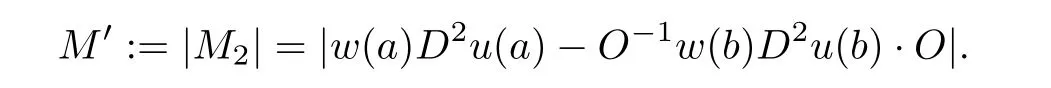
Then

for a positive constant C3(δ)depending only on δ.Forwe can take
ProofIndeed forThen by homogeneity,

For the generalδ,the argument remains valid and permits to take
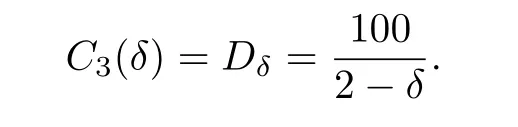
End of Proof of Theorem 1.2Wecan now prove the uniform hyperbolicity of M(a,b,O),and thus the theorem.In fact,forone can take C=2000 in Lemma 2.1 for c=106.
Indeed,we have

Therefore,

and

Thus

sinceTherefore,for a sufficiently large c,we get

since M ≥ C2(δ)K which finishes the proof.Taking forthe values


AcknowledgementsThe authors are deeply grateful to the anonimous referee whose advise permitted to ameliorate significantly our exposition.
[1]Caffarelli,L.,Interior a priory estimates for solutions of fully nonlinear equations,Ann.Math.,130,1989,189–213.
[2]Caffarelli,L.and Cabre,X.,Fully nonlinear elliptic equations,American Mathematical Society Colloquium Publications,43,Amer.Math.Soc.,Providence,RI,1995.
[3]Crandall,M.G.,Ishii,H.and Lions,P.-L.,User’s guide to viscosity solutions of second order partial differential equations,Bull.Amer.Math.Soc.(N.S.),27,1992,1–67.
[4]Nadirashvili,N.and Vlǎdut?,S.,Singular solutions of Hessian elliptic equations in five dimensions,J.Math.Pures Appl.,100(9),2013,769–784.
[5]Nadirashvili,N.and Vlǎdut?,S.,Singular solutions of Hessian fully nonlinear elliptic equations,Adv.Math.,228,2011,1718–1741.
[6]Nadirashvili,N.,Tkachev,V.G.and Vlǎdut?,S.,Nonlinear elliptic equations and nonassociative algebras,Math.Surv.and Monogr.,200,Amer.Math.Soc.,Providence,RI,2014.
[7]Tkachev,V.G.,A Jordan algebra approach to the eiconal,J.of Algebra,419,2014,34–51.
[8]Trudinger,N.,H?lder gradient estimates for fully nonlinear elliptic equations,Proc.Roy.Soc.Edinburgh Sect.A,108,1988,57–65.
[9]Trudinger,N.,Fully nonlinear elliptic equations in geometry.CBMS Lectures,October 2004 draft.http://maths?people.anu.edu.au/e neilt/RecentPapers/notes1.pdf
 Chinese Annals of Mathematics,Series B2017年2期
Chinese Annals of Mathematics,Series B2017年2期
- Chinese Annals of Mathematics,Series B的其它文章
- CR Geometry in 3-D?
- A Third Derivative Estimate for Monge-Ampere Equations with Conic Singularities
- Symmetrization for Fractional Elliptic and Parabolic Equations and an Isoperimetric Application?
- The Mathematical Theory of Multifocal Lenses?
- Convergence to a Single Wave in the Fisher-KPP Equation?
- Negative Index Materials and Their Applications:Recent Mathematics Progress
