A new non-specificity measure in evidence theory based on belief intervals
Yng Yi,Hn Deqing,Jen Dezert
aSKLSVMS,School of Aerospace,Xi'an Jiaotong University,Xi'an 710049,China
bCenter for Information Engineering Science Research,Xi'an Jiaotong University,Xi'an 710049,China
cONERA,The French Aerospace Lab,Chemin de la Hunie`re,F-91761 Palaiseau,France
A new non-specificity measure in evidence theory based on belief intervals
Yang Yia,Han Deqiangb,*,Jean Dezertc
aSKLSVMS,School of Aerospace,Xi'an Jiaotong University,Xi'an 710049,China
bCenter for Information Engineering Science Research,Xi'an Jiaotong University,Xi'an 710049,China
cONERA,The French Aerospace Lab,Chemin de la Hunie`re,F-91761 Palaiseau,France
In the theory of belief functions,the measure of uncertainty is an important concept,which is used for representing some types of uncertainty incorporated in bodies of evidence such as the discord and the non-specificity.For the non-specificity part,some traditional measures use for reference the Hartley measure in classical set theory;other traditional measures use the simple and heuristic function for joint use of mass assignments and the cardinality of focal elements.In this paper,a new non-specificity measure is proposed using lengths of belief intervals,which represent the degree of imprecision.Therefore,it has more intuitive physical meaning.It can be proved that our new measure can be rewritten in a general form for the non-specificity.Our new measure is also proved to be a strict non-specificity measure with some desired properties.Numerical examples,simulations,the related analyses and proofs are provided to show the characteristics and good properties of the new non-specificity definition.An example of an application of the new nonspecificity measure is also presented.
1.Introduction
The theory of belief functions1is an important tool for uncertainty modeling and reasoning.It can distinguish the'unknown'and the'imprecision'and provides a method forfusing different evidences by using the commutative and associative Dempster's rule of combination.The theory of belief functions has been widely used in the fields of information fusion,2pattern classification,3–5and multiple attribute decision making,6,7etc.Some modified or extended frameworks including the transferable belief model(TBM)8and Dezert-Smarandache theory(DSmT)9were also proposed by researchers in the past decades.
The measure of uncertainty10–12is very crucial in all kinds of theories of uncertainty.The concept of uncertainty is intricately connected to the concept of information.Therefore,to describe the uncertainty,measures in information theory are often used for reference.E.g.,in probability theory,the Shannon entropy13is developed.In fuzzy set theory14and its related applications,15,16some entropy-alike measures also are proposed to represent the uncertainty.17Also,in the theory of belief functions,many entropy-alike measures are proposed such as the ambiguity measure(AM),10the aggregated uncertainty(AU)measure18to measure the total uncertainty in a basic belief assignment(BBA).Actually,in a BBA,there are two types of uncertainty.10One is the discord(or randomness or conflict).Another is the non-specificity.They can be unified under the term ambiguity.
Forthediscord part,many Shannon entropy-alike measures were introduced by researchers.19Nonspecificity10,18,20–22means two or more alternatives are left unspecified,which represents a degree of imprecision.It only focuses on those focal elements with cardinality larger than 1.Non-specificity is a distinctive uncertainty type in the theory of belief functions when compared with the probability theory.Therefore,in this paper,we focus on the non-specificity part.There are also some non-specificity measures proposed.21,23,24The most typical one23is a generalization of the Hartley measure,25which is originally for the classical set theory.In probability theory,there is only discord(or randomness or conflict).10Other available non-specificity measures21,24use the simple and heuristic function for joint use of mass assignments and the cardinality of focal elements.
In this paper,we aim to design a new non-specificity measure without using the measure of classical set theory or using heuristic joint use of mass assignments and the cardinality of the focal elements,but to design using intuitive physical explanations of the uncertainty in the theory of belief functions.As aforementioned,the non-specificity actually represents a kind of imprecision.In the theory of belief functions,the precision is often modeled by lengths of the belief intervals.The mean of the belief intervals' lengths for all singletons is defined as the non-specificity.Therefore,our new definition can be considered as an averaging imprecision of different singletons.Furthermore,the new measure can be rewritten to a general form of non-specificity measure and it has several desired properties for uncertainty measures.
The rest of this paper is organized as follows.In Section 2,the essentials of the theory of belief functions are introduced.Some available uncertainty measures,especially the nonspecificity measures in the theory of belief functions are briefly introduced in Section 3.In Section 4,a novel non-specificity measure is proposed.Some desired properties are provided together with related proofs.In Section 5,we use some numerical examples and simulations to show the rationality of the proposed new non-specificity measure,where the comparisons between the available measures and the new one are provided.Also,an example of the application of the new non-specificity measure is given in Section 6.Section 7 concludes this paper.
2.Basics of the theory of belief functions
In the theory of belief functions,also called Dempster–Shafer evidence theory(DST)1,the basic concept is the frame of discernment(FOD),which is a discrete and finite set.The elements in FOD are mutually exclusive and exhaustive.Given an FOD Θ,on its power set 2Θ,a BBA m:2Θ→ [0,1]can be defined satisfying
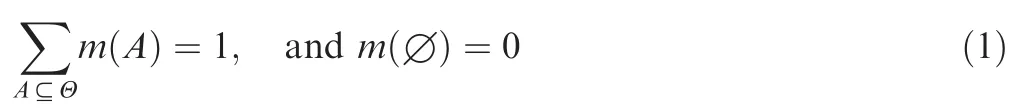
A BBA is also called a mass function.All the A with m(A)gt;0 are called focal elements of a BBA m(.).The set of all the focal elements denoted byfand their corresponding mass assignments m constitute a body of evidence(BOE):(F,m).Based on the definition of BBA in Eq.(1),the belief function(Bel)and the plausibility function(Pl)are defined for any A?Θ as follows1:

The belief function and plausibility function can be interpreted as a lower and a upper bound of the probability P(A),respectively,i.e.,P(A)∈[Bel(A),Pl(A)],which is a belief interval of the focal element A.The length of the belief interval Len(A)=Pl(A)-Bel(A)represents the degree of imprecision for A.1
The mass assignment for the total set Θ,i.e.,m(Θ)represents the degree of ignorance(or unknown)for a given BBA m.Therefore,the theory of belief functions can discriminate the''imprecisionquot;and the''ignorancequot;.
In the theory of belief functions,independent BBAs(m1,m2)are combined using Dempster's rule of combination as follows1:

where Aiand Bjdenote the focal element of m1and m2,respectively.K denotes the conflict coefficient between m1and m2.Note that the BBAs to be combined using Dempster's rule should be independent.The research related to the dependent BBAs can found in Ref.26Dempster's rule of combination is both associative and commutative.There exist many other alternative combination rules,see details in Refs.9,27
DST has been argued for its drawbacks in past decades.28–31Some modified or improved frameworks were also proposed including the TBM8and DSmT.9
3.Uncertainty measures in the theory of belief functions
There are various kinds of uncertainty,10e.g.,the fuzziness,randomness(or discord or conflict),non-specificity,which can be represented and processed by different types of uncertainty theories.10,11In the theory of belief functions,a BBA has two types of uncertainty,i.e.,the discord and the nonspecificity,hence ambiguity.10Many uncertainty measures were proposed for the discord,the non-specificity,and the total uncertainty(including both two parts).
3.1.Measures for discord in the theory of belief functions
Measures for discord is to depict the randomness(or discord or conflict)in a BOE.Available measures for discord in the theory of belief functions are listed below.Although with different names,they are all for the discord part of the uncertainty in the theory of belief functions.
(1)Confusion measure(1982)
The confusion measure is proposed by Hohle32as

(2)Dissonance measure(1983)
The dissonance measure is proposed by Yager21as

(3)Discord measure(1990)
The discord measure Disc is proposed by Klir and Ramer33as
(4)Strife measure(1992)
The strife measure Strif is proposed by Klir and Parviz34
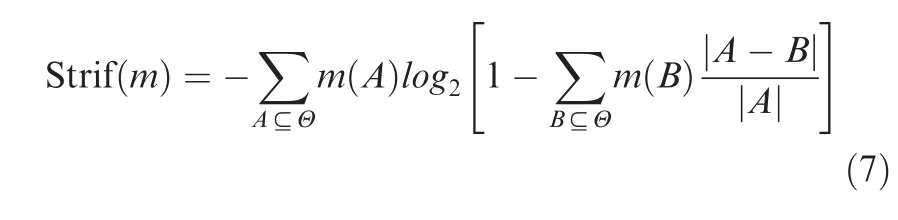
As we can see,they are all Shannon entropy-alike measure.The differences and relationships between the measures above can be found in Refs.19,34
3.2.Measures for non-specificity in the theory of belief functions
Non-specificity20,21,23,35means two or more alternatives are left unspecified.It represents a degree of imprecision and only focus on those focal elements with cardinality larger than one.Non-specificity is a distinctive uncertainty type in the belief functions framework when compared with the probabilistic framework.So,the non-specificity is mainly concerned here.The available non-specificity measures are as follows.
(1)Duboisamp;Prade's non-specificity23

It is a generalized Hartley measure25from the classical set theory to the belief functions framework.When the BBA m(.)is a Bayesian BBA,i.e.,it only has singleton focal elements,it reaches the minimum value 0.When BBA m(.)is a vacuous BBA,i.e.,m(Θ)=1,it reaches the maximum value log2(|Θ|).In fact,due to log21=0,the mass assignments of singletons are nuisances in the computation of NSDP.This definition was proved to have the uniqueness by Ramer22,that is,it satisfies all the expected requirements of the nonspecificity measure.20,22
(2)Yager's specificity21

The maximum value is 1(when the BBA is Bayesian);the minimum value is 1/|Θ|(when the BBA is vacuous).One can use 1-SY(m)to denote the non-specificity.
Actually,here the mass assignments of singletons are involved in the computation.
(3)Korner's non-specificity24

The maximum value is|Θ|(vacuous BBA);the minimum value is 1(Bayesian BBA).Actually,here the mass assignments of singletons are involved in the computation.
(4)In Korner's work,a general form of the non-specificity(or specificity)measure is proposed as

As referred in Ref.24,if a measure satisfies Eq.(11),it is a non-specificity measure(function).
3.3.Measures for total uncertainty in the theory of belief functions
(1)AU18
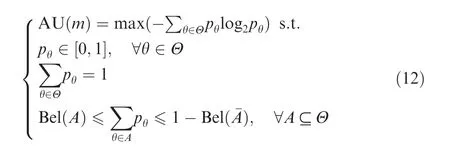
It is also called the''upper entropyquot;.AU is an aggregated total uncertainty(ATU)measure,which can capture both non-specificity and discord.AU satisfies all the requirements for uncertainty measure including probability consistency,set consistency,value range,subadditivity and additivity for the joint BBA in Cartesian space.35
(2)AM

Note that non-specificity can also be de fined in the framework of fuzzy sets37or intuitionistic fuzzy sets.38Here what we are concerned is the non-specificity in the theory of belief functions.
4.Novel non-specificity measure based on the length of the belief intervals
As we can see in the previous section,traditional nonspecificity measures are either the generalization of the Hartley measure in classical set theory,or the one heuristically built from the joint use of the cardinality and the mass assignment of the BBA.We do not prefer such expedient ways and aim to design a new non-specificity measure directly using the intuitive concept of uncertainty in the framework of belief functions.The new measure is introduced below.
4.1.Definition of new non-specificity measure in the theory of belief functions
Non-specificity is in fact a kind of imprecision for different propositions in FOD.In the framework of belief functions,the degree of imprecision for each proposition A is represented by the length of the corresponding focal element's belief interval[Bel(A),Pl(A)].Given an FOD Θ ={θ1,θ2,...,θn},the belief interval for each singleton{θi},i.e.,[Bel({θi}),Pl({θi})]can be obtained together with n belief intervals' lengths Len(i)=Pl({θi})-Bel({θi}).We define the mean of all the n belief intervals' lengths as the new non-specificity as follows.

Here,BI denotes the belief interval.NSBI(m)represents the averaging imprecision in m,i.e.,the non-specificity.To avoid the redundant use of the imprecision for each singleton,here we only use the belief intervals of singletons.
Since

then,?i=1,2,...,n,

Therefore,the non-specificity definition in Eq.(14)can be rewritten as

So,it is actually the weighted summation of the normalized cardinality size of the focal elements except for singletons,where the weights are their mass assignments.That is to say in computation of our belief interval-based non-specificity,there is no need to calculate the belief intervals but to just follow the final step in Eq.(17)with simple multiplication and summation operations.Eq.(17)can be further rewritten as

where δ(.)is the Dirac delta function defined as

Eq.(18)satisfies the general form in Eq.(11)if

So,the definition in Eq.(14)is a non-specificity measure.According to Eqs.(14)and(18),obviously,NSBI(m)reaches its minimum value 0,when m is a Bayesian BBA;NSBI(m)reaches its maximum value 1,when m is a vacuous BBA.It should be noted that our new measure expressed by Eq.(17)has two differences with that in NSK,although the Eqs.(10)and(17)have closely similar expressions.The first difference is that in our new definition in Eq.(17),singletons are not involved in computation.Actually,the mass assignments are canceled in the calculation of the singletons' belief intervals' lengths.However,in NSK,mass assignments of singletons are used.The second difference is that,our definition has a normalization factor n while NSKhas no such a factor.
Note that NSBI(m)has many desired properties for an uncertainty measure as analyzed in the next subsection.
4.2.Desired properties of new non-specificity measure
(1)Range
As aforementioned,NSBI(m)reaches its minimum value 0,when m is a Bayesian BBA;NSBI(m)reaches its maximum value 1,when m is a vacuous BBA.This means that a Bayesian BBA corresponds to a maximally precise statement,while a BBA expressing total ignorance represents the most non-specific(or the most imprecise)statement on the FOD.20
Our new non-specificity measure in Eq.(14)satisfies the monotonicity.See the proof below.
Proof.If ?A∈P(Θ):Bel1(A)≥Bel2(A),Pl1(A)≤Pl2(A),then there exists

Therefore,

End of Proof□
(3)Symmetry If two BBAs m1,m2assign the same summation of mass assignment values to focal elements with the same cardinality,then the non-specificity values of the two BBAs are equal.This is called symmetry.22
Our new non-specificity measure in Eq.(14)satisfies the symmetry.See the proof below.

End of Proof□
(4)Multiplicativity for joint BBAA joint BBA10m:P(ΘXXΘY)→[0,1]is a BBA defined on the Cartesian product of two sets(two distinct FODs)ΘXwith cardinality nΘXand ΘXwith cardinality nΘY,where P(ΘXXΘY)is the power set of ΘXX ΘY.Suppose that f is a set of focal elements of the joint BBA on the joint FOD ΘXXΘY,and S∈ F.
The projections of S on to ΘXis denoted by Sx={x ∈ΘX|(x,y)∈S,?x ∈ΘX}.The projections of S on to ΘYis denoted by Sy={y∈ΘY|(x,y)∈S,?y∈ΘY}.Then,the marginal BBAs can be defined as10

If m(.)=mΘXXmΘYis a joint BBA on ΘXX ΘY,and two independent marginal BBAs are mΘX(.)and mΘY(.)then
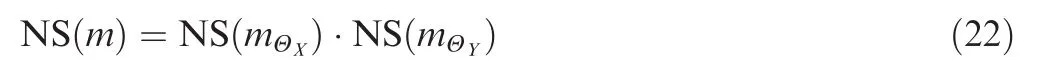
This is called the property of multiplicativity.
Our new non-specificity measure in Eq.(14)satisfies the multiplicativity.20See the proof below.
Proof.

End of Proof□
(5)Sub-multiplicativity for joint BBAIfis a joint BBA on ΘXX ΘY,and its marginal BBAs mΘX(.)andwhich are unknown to be independent or not,then,This is called the property of sub-multiplicativity.The''=quot;holdsonly when mΘX(.)and mΘY(.)are independent.
Note that the physical meaning of sub-multiplicativity is in essential the conservation of information,i.e.,the amount of uncertainty in a joint BBA is no greater than the total amount of uncertainty of its corresponding marginal BBAs.The equation holds if and only if the corresponding marginal BBAs are independent,i.e.,there is not correlated part.If two marginal BBAs are dependent,then the double counting uncertainty amount should be removed,therefore,the total amount of uncertainty in the joint BBA is larger than the total amount in marginal BBAs.
Proof.Suppose that S is the focal element in Cartesian space ΘXXΘY;proj(S;ΘX)=Sxand proj(S;ΘY)=Syrepresent the projections of S on ΘXand ΘY,respectively.
The non-specificity NSBIof two marginal BBA mΘX(.)and mΘY(.)are

The multiplication of the NSBIfor two marginal BBAs are

End of Proof□
It should be noted that Duboisamp;Prade's non-specificity in Eq.(8)also satisfies all the properties including the monotonicity,the symmetry,the additivity(which is the counter-part of the multiplicativity here),and the sub-additivity(which is the counter-part of the sub-multiplicativity here).20Here we provide detailed explanations for the additivity and sub-additivity.
If m(.)is a joint BBA on ΘXXΘY,and the associated marginal BBAsmΘX(.)and mΘY(.)are independent,then NSDP(m)=NSDP(mΘX)+NSDP(mΘY)because of log function involved in the definition of NS measure in Eq.(8).This is called the property of additivity.The additivity is in essential equivalent to the multiplicativity,i.e.,they both describe the relationship between the non-specificity of a joint BBA and their corresponding independent marginal BBAs.
If the marginal BBAs mΘX(.)and mΘY(.)are unknown to be independent or not,then NSDP(m)≤ NSDP(mΘX)+NSDP(mΘY).This is called the property of sub-additivity.The sub-additivity is in essential equivalent to the sub-multiplicativity.
Therefore,both Duboisamp;Prade's non-specificity in Eq.(8)and our new measure in Eq.(14)strictly satisfy all the requirements(properties)of a non-specificity measure.Not all the requirements or properties can be satisfied for Yager's definition and Kornor's definition.Our new definition in Eq.(14)and Duboisamp;Prade's definition in Eq.(8)can both be used as a strict non-specificity measure.Our new measure can be a good alternative of the traditional strict NSDP.We want to emphasize that the theoretic consistency is an very important issue when one defines some measure under a given theoretic framework.Our proposed measure keeps the consistency,thus,it is not the generalization of any measure in other frameworks.In the next section,some illustrative examples and simulations are provided to show the rationality of our new non-specificity measure.
5.Illustrative examples and simulations
5.1.Example 1
Suppose that the FOD Θ ={θ1,θ2,θ3}.A BBA defined on Θ is m(A)=1,?A= Θ.At each step,m(Θ)has a decrease of Δ =0.05 and each singleton mass m({θi}),i=1,2,3 has an increase of Δ/3.At the final step,m(Θ)becomes zero and m({θi})=1/3,i=1,2,3.At each step,Duboisamp;Prade's non-specificity (NSDP), Yager's non-specificity (NSY),Kornor's non-specificity(NSK),our proposed belief interval based non-specificity(NSBI),total uncertainty measure AU and AM(they also include the non-specificity part according to their definitions)are calculated.The changes of these uncertainty values at different steps are illustrated in Fig.1.
As shown in Fig.1,all non-specificity measures decrease with the increase of the mass assignments for singletons and the decrease of the mass assignment for Θ.All the non-specificity measures compared here reach their minimum value when m becomes a Bayesian BBA,and they reach their maximum value when m is a vacuous BBA.They all provide rational behavior.Our proposed NSBI∈[0,1]has natural normalization.Such a value range is more preferred as an uncertainty measure.Both of the minimum values of NSYand NSDPare 0.Therefore,by using normalization factor,they can have the value range of[0,1].However,the minimum value of NSKis 1 but not 0,which is not preferred.

Fig.1 Change of different non-specificity measures and total uncertainty measures in Example 1.
For the total uncertainty measure AU and AM,they never change in the whole procedure(at their maximum value).Although AU and AM declare that they can also depict the non-specificity part in the total uncertainty,they cannot discriminate the changes of BBAs at each step.This is because they are defined based on some probabilistic transformation from BBAs.In this example,for the probabilistic transformation used in AM and AU,the results are always a uniformly distributed probability mass function(p.m.f.)P(θi)=1/3,i=1,2,3,therefore AM and AU will never change here.According to our opinion,it is not judicious to define total uncertainty measure in the theory of belief functions by using for reference the uncertainty measure in probability framework,i.e.,Shannon entropy.It should be better not to switch the framework but to directly design in the framework of belief functions.This is also our concerns and motivations for the design of belief interval based non-specificity measure.
5.2.Example 2
Suppose that the FOD Θ ={θ1,θ2,θ3}.A BBA defined on Θ is m(A)=1,?A= Θ.At each step,m(Θ)has a decrease of Δ =0.05 and one singleton mass m({θ1})has an increase of Δ.In the final step,m(Θ)becomes zero and m({θ1})=1.The changes of these uncertainty values(including NSDP,NSY,NSK,NSBI,AU and AM)at different steps are illustrated in Fig.2.

Fig.2 Change of different non-specificity measures and total uncertainty measures in Example 2.
At the first step,the BBA is a vacuous one,and at the last step,the BBA is a categorical one.So,each uncertainty measure changes from their maximum value to the minimum value.In this example,AM and AU can also bring intuitive results because at each step the probabilistic transformation results are not always uniformly distributed p.m.f.
Although in this simple case,all compared measures perform well,it should be noted that some traditional measures will bring counter-intuitive behaviors as shown in the following examples.
5.3.Example 3
Suppose that the FOD is Θ ={θ1,θ2,θ3,θ4}.A BBA defined on Θ is m(A)=1,?A={θ1,θ2}.At each step,m(A)has a decrease of Δ=0.05,and the other focal elements with cardinality of 2(including{θ1,θ3},{θ1,θ4},{θ2,θ3},{θ2,θ4},{θ3, θ4})increase Δ/5=0.01.At the final step,m(B)=1/6,?|B|=2.The changes of these uncertainty values(including NSDP,NSY,NSK,NSBI,AU and AM)at different steps are illustrated in Fig.3.
Since in the whole procedure,all the focal elements'cardinality is 2,all the non-specificity measures do not change.The total uncertainty AM and AU increase at each step and reach their maximum value finally.This is because that the probabilistic transformations of the BBAs gradually approach a uniformly distributed p.m.f.with the change of the BBA at each step.
5.4.Example 4
Suppose that the FOD Θ ={θ1,θ2}.A BBA defined on Θ is m({θ1})=a,m({θ2})=b,m(Θ)=1-a-b,where a,b ∈[0,0.5].We calculate all the uncertainty values(including NSDP,NSY,NSK,NSBI,AU and AM).The change of different uncertainty measures with the change of a and b is illustrated in Fig.4.

Fig.3 Change of different non-specificity measures and total uncertainty measures in Example 3.
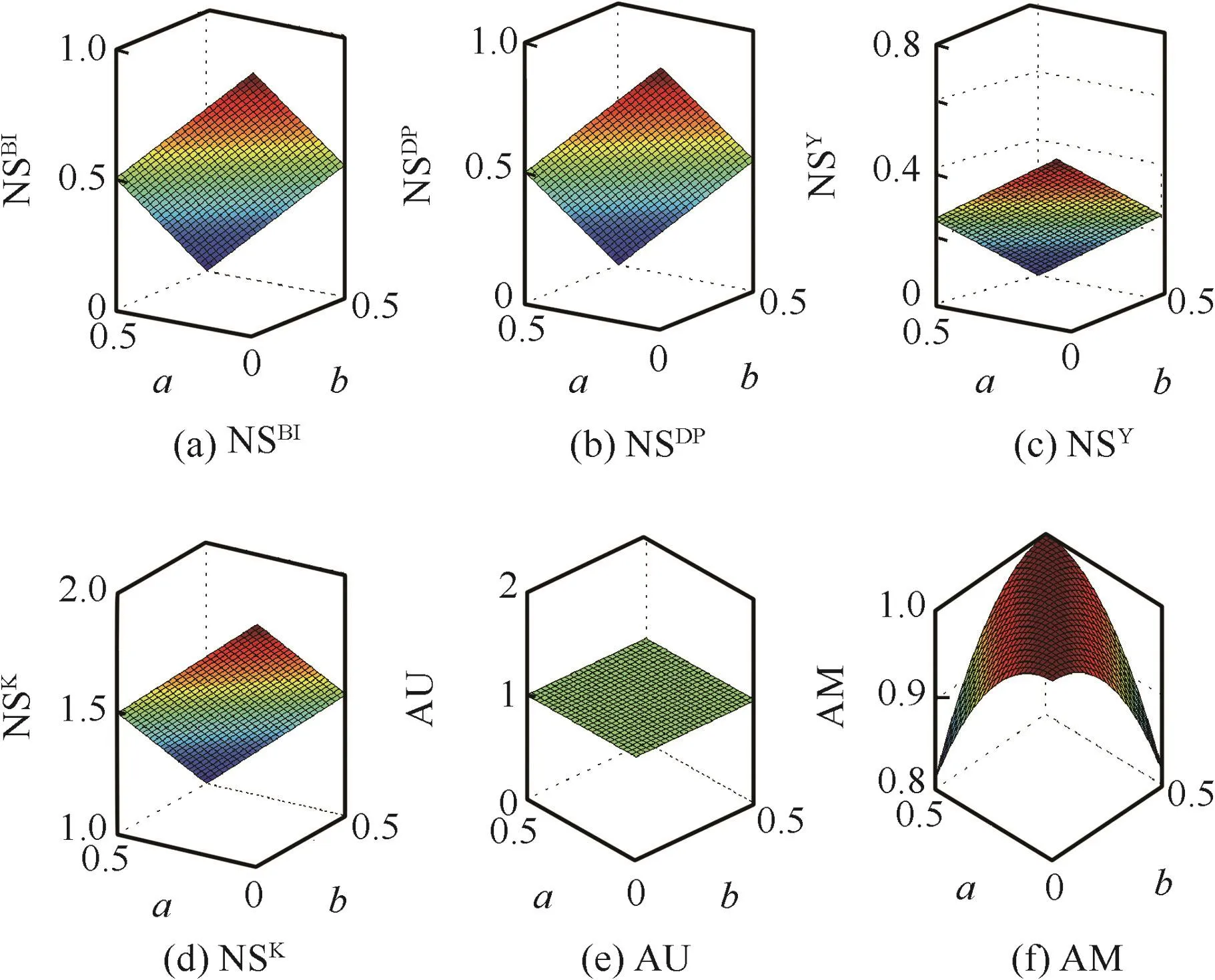
Fig.4 Change of different non-specificity measures and total uncertainty measures in Example 4.
As shown in Fig.4,the values of NSDPand NSBIare the same,because log2|A|=|A|/2,?|A|=2.All non-specificity measures reach their maximum values when a=b=0,i.e.,m(Θ)=1, and reach their minimum values when a=b=0.5,i.e.,m(Θ)=0.Since AU tries to find a p.m.f.with maximum Shannon entropy,and the uniformly distributed P(θ1)=P(θ2)=0.5 always satisfies the constraints above(because a,b∈[0,0.5]),no matter how a and b change,therefore,P(θ1)=P(θ2)=0.5 is always picked up when calculating AU and thus,AU always equals log22=1.AM reaches its maximum value when a=b,because for a=b,the corresponding pignistic probability of the BBA is uniformly distributed.
5.5.Example 5
This example is used for reference from.10Given the size of the FOD |Θ|=5.Randomly generate 10 BBAs with k(1≤k≤31)focal elements according to algorithm39in Table 1.Here,we set the number of focal elements to a fixed value 15.
These generated 10 BBAs(m1,m2,...,m10)are then combined one by one using Dempster's rule of combination,respectively. At each combination instant t:where t=1,2,...,9,and we start withThe values for NSDP,NSY,NSK,NSBI,AU and AM of the combination result at t are calculated forThe whole procedure is repeated 100times and the average values of different uncertainty measures at different instants are shown in Fig.5.

Table 1 Algorithm:Random generation of BBA.
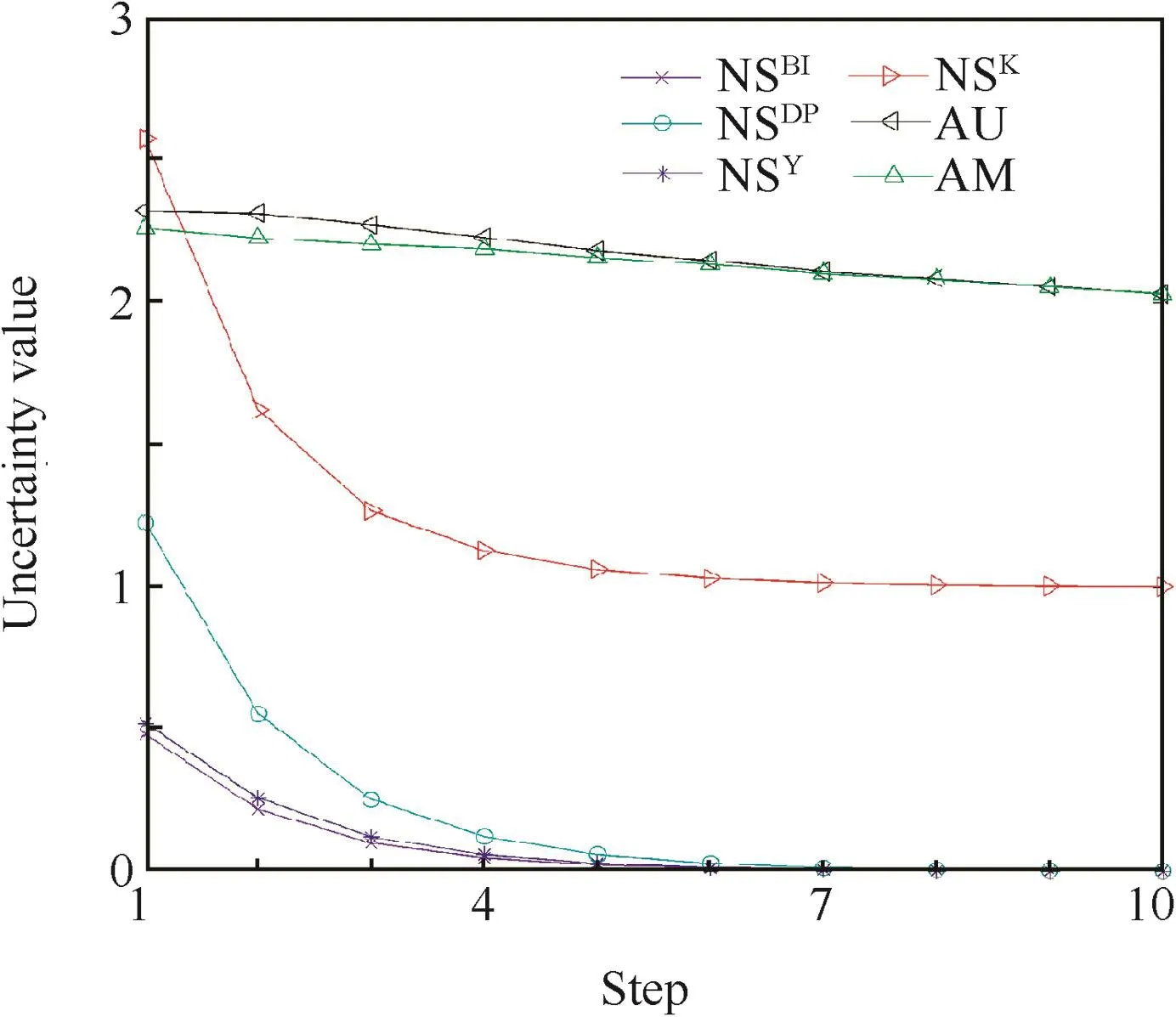
Fig.5 Change of different non-specificity measures and total uncertainty measures in Example 5.
As shown in Fig.5,all the uncertainty measures compared here decrease with the increase of the combination steps.This makes sense,because it is intuitive that the uncertainty decreases in the information fusion procedure like the evidence combination.The non-specificity measures drop faster and more significantly than the total uncertainty measures.This is because that in the evidence combination based on Dempster's rule,the focal elements are split into focal elements with smaller cardinality.
As we can see in the above examples,our new proposed belief interval-based non-specificity measure is rational and effective in representing the non-specificity in BBAs.
6.Application of belief interval-based non-specificity measure
Uncertainty measures including the non-specificity measure have be used in many applications such as the weighted evidence combination.40,41Here we provide an example of using our new non-specificity in feature evaluation for pattern recognition to further show the rationality of the proposed measure.
We artificially generate three classes of samples.Each class has 100 samples.Each sample has 3 dimensions.In each class,each dimension of the samples is Gaussian distributed with different mean and standard deviation(Std)values as illustrated in Fig.6 and Table 2.

Table 2 Gaussian distribution parameters of the samples.
As we can see in Fig.6 and Table 2,the class discrimination capability of Feature 2 is the best,because the three Gaussian probability density functions(PDFs)are quite well separated;that of Feature 3 is the worst,and that of the Feature 1 is in the middle.This can also be verified by using the discrimination criterion as follows.

where tr(.)denotes the trace of a matrix.Suppose that there are C classes and each class Cihas Nisamples.The degree of inner class cohesion Swand the degree of inter-class separability Sbare as follows.42

where X is feature(s)of a sample and

is the mean of all the classes' centroids.If J of some feature(or set of features)in Eq.(23)is smaller,then such a feature(or set of features)is more crisp and discriminable.
For our artificially generated samples J(1)=0.2557,J(2)=0.1013,J(3)=326.8135,which means that Feature 2 is the best,Feature 3 is the worst,and Feature 1 is in the middle.
First,we use the following way43to generate BBAs for each sample xqon different feature i∈{1,2,3}.

Fig.6 Probability density function of different features of the samples belonging to three classes.

Fig.7 Illustration of BBA generation.

where dqjdenotes the distance between the query sample xqand the class Aj.Parameters α =1,β =2 as suggested in Ref.43It should be noted that in the original form in Ref.43,there exists the mass assignment for the emptyset ?representing the possibility of xqto be an outlier.In this paper,we only concern the closed-world assumption,i.e.,there is no mass assignment for?.Here we give an illustrative example in Fig.7.
In Fig.7,three different colors represent three different classes.c1denotes the centroid of samples in Class 1;c1,2denotes the centroid of samples in Class 1 and Class 2;c1,2,3denotes the centroid of samples in Class 1,2,and 3.Calculate the distance d between xqand those centroids of single classes and compound classes.Then according to Eq.(26),the BBA can be generated.
Second,we calculate NSBIfor all the BBAs generated.Then calculate the average values of NSBIfor different featureias

The averaging non-specificity of a feature is larger,then it is more discriminable.
For our artificially generated samples illustrated in Fig.6 and Table 2,

This is consistent with the intuition and the feature evaluation based on the discrimination criterion in Eq.(23).
7.Conclusions
A novel strict non-specificity measure in the theory of belief functions is proposed with several desired properties.It should be noted that the new measure is defined directly in the framework of belief functions.There is no need to switch(and thus lose information)from belief functions to the classical probabilistic framework.Numerical examples,simulations,and the application of the new measure are also provided,which show that the new measure can well measure the non-specificity in a BBA and can be effectively used in applications such as feature evaluation.
In future work,we attempt to apply our new measure in other applications such as the weighted evidence combination,etc.We will also research on the other part of uncertainty,i.e.,the discord,and the total uncertainty directly in the framework of belief functions(not transforming to the probability framework).There are already some related tentative related works on this.44–46
Acknowledgements
This work was supported by the Grant for State Key Program for Basic Research of China(No.2013CB329405),National Natural Science Foundation of China(No.61573275),Foundation for Innovative Research Groups of the National Natural Science Foundation of China(No.61221063),Science and Technology Project of Shaanxi Province of China(No.2013KJXX-46),Specialized Research Fund for the Doctoral Program of Higher Education of China(20120201120036),and Fundamental Research Funds for the Central Universities of China(No.xjj2014122).
1.Shafer G.A mathematical theory of evidence.Princeton,NJ:Princeton University Press;1976.p.35–60.
2.Lin GP,Liang JY,Qian YH.An information fusion approach by combining multigranulation rough sets and evidence theory.Inf Sci 2015;314:184–99.
3.Dong GG,Kuang GY.Target recognition via information aggregation through Dempster–Shafer's evidence theory.IEEE Geosci Remote Sensing Lett 2015;12(6):1247–51.
4.Liu ZG,Pan Q,Mercier G,Dezert J.A new incomplete pattern classification method based on evidential reasoning.IEEE Trans Cybernetics 2015;45(4):635–46.
5.Lian C,Ruan S,Den?ux T.An evidential classifier based on feature selection and two-step classification strategy.Pattern Recogn 2015;48(7):2318–27.
6.Han D,Dezert J,Tacnet J-M,Han C.A fuzzy-cautious OWA approach with evidential reasoning.2012 15th international conference on information fusion(FUSION);2012 July 9–12;Singapore.Piscataway,NJ:IEEE Press;2012.p.278–85.
7.Liu JP,Liao XW,Yang JB.A group decision-making approach based on evidential reasoning for multiple criteria sorting problem with uncertainty.Eur J Oper Res 2015;246(3):858–73.
8.Smets P,Kennes R.The transferable belief model.Artif Intell 1994;66(2):191–234.
9.Smarandache F,Dezert J.Advances and applications of DSmT for information fusion-collected works-Volume 3. Rehoboth,USA:American Research Press;2009.
10.Jousselme AL,Liu CS,Grenier D,Bossé é.Measuring ambiguity in the evidence theory.IEEE Trans Syst Man Cybernetics Part A 2006;36(5):890–903.
11.Klir GJ.Uncertainty and information measures for imprecise probabilities:an overview.1999 1st international symposium on imprecise probabilities and their applications(ISIPTA);1999 June 29–July 2;Ghent,Belgium.1999.p.234–40.
12.Bronevich A,Klir GJ.Measures of uncertainty for imprecise probabilities:an axiomatic approach.Int J Approximate Reasoning 2010;51(4):365–90.
13.Shannon CE.A mathematical theory of communication.Bell Syst Tech J 1949;27(3):379–423.
14.Zadeh LA,Klir GJ,Yuan B.Fuzzy sets,fuzzy logic,and fuzzy systems:selected papers.River Edge,NJ,USA:World Scientific Publishing Co.Inc.;1996.p.1–20.
15.Zhang HG,Zhang JL,Yang GH,Luo YH.Leader-based optimal coordination control for the consensus problem of multiagent differential games via fuzzy adaptive dynamic programming.IEEE Trans Fuzzy Syst 2015;23(1):152–63.
16.Zhang HG,Cai LL,Bien Z.A fuzzy basis function vector-based multivariable adaptive controller for nonlinear systems.IEEE Trans Syst Man Cybernetics Part B 2000;30(1):210–7.
17.Hwang CM,Yang MS.On entropy of fuzzy sets.Int J Uncertainty Fuzziness Knowledge Based Syst 2008;16(4):519–27.
18.Harmanec D,Klir GJ.Measuring total uncertainty in Dempster–Shafer theory–a novel approach.Int J Gen Syst 1994;22(4):405–19.
19.Pal NR,Bezdek JC,Hemasinha R.Uncertainty measures for evidential reasoning I:A review.Int J Approximate Reasoning 1992;7(3):165–83.
20.Dubois D,Prade H.Properties of measures of information in evidenceand possibility theories.Fuzzy SetsSyst1987;24(2):161–82.
21.Yager RR.Entropy and specificity in a mathematical theory of evidence.Int J Gen Syst 1983;9(4):249–60.
22.Ramer A.Uniqueness of information measure in the theory of evidence.Fuzzy Sets Syst 1987;24(2):183–96.
23.Dubois D,Prade H.A note on measures of specificity for fuzzysets.Int J Gen Syst 1985;10(4):279–83.
24.Korner R,Nather W.On the specificity of evidences.Fuzzy Sets Syst 1995;71(2):183–96.
25.Hartley RV.Transmission of information.Bell Syst Tech J 1928;7(3):535–63.
26.Su XY,Mahadevan S,Xu PD,Deng Y.Handling of dependence in Dempster–Shafer theory.Int J Intell Syst 2015;30(4):441–67.
27.Liu ZG,Dezert J,Pan Q,Mercier G.Combination of sources of evidence with different discounting factors based on a new dissimilarity measure.Decis Support Syst 2011;52(1):133–41.
28.Zadeh LA.A simple view of the Dempster–Shafer theory of evidence and its implication for the rule of combination.AI Mag 1986;7(2):85.
29.Wang P.A defect in Dempster-Shafer theory.1994 10th international conference on uncertainty in artificial intelligence(UAI);1994 July 29–31;Seattle,Washington,USA.1994.p.560–6.
30.Voorbraak F.On the justification of Dempster's rule of combination.Artif Intell 1991;48(2):171–97.
31.Pearl J.Reasoning with belief functions:an analysis of compatibility.Int J Approximate Reasoning 1990;4(5):363–89.
32.Hohle U.Entropy with respect to plausibility measures.1982 12th IEEE international symposium on multiple valued logic(ISMVL);1982 May 24–27;Paris,France.Piscataway,NJ:IEEE Press;1982.p.167–9.
33.Klir GJ,Ramer A.Uncertainty in the Dempster–Shafer theory – a critical reexamination.Int J Gen Syst 1990;18(2):155–66.
34.Klir GJ,Parviz B.A note on the measure of discord.1992 8th annual conference on uncertainty in artificial intelligence;1992 July 17–19;Stanford,CA,USA.1992.p.138–41.
35.Abellan J,Masegosa A.Requirements for total uncertainty measures in Dempster–Shafer theory of evidence.Int J Gen Syst 2008;37(6):733–47.
36.Klir GJ,Lewis HW.Remarks on measuring ambiguity in the evidence theory.IEEE Trans Syst Man Cybernetics Part A 2008;38(4):995–9.
37.Garmendia L,González-del-Campo R,Yager RR.Recursively spreadable and reductible measures of specificity.InfSci 2016;326:270–7.
38.Song YF,Wang XD,Yu XD,Zhang HL,Lei L.How to measure non-specificity of intuitionistic fuzzy sets.J Intell Fuzzy Syst 2015;29(5):2087–97.
39.Jousselme AL,Maupin P.Distances in evidence theory:comprehensive survey and generalizations.Int J Approximate Reasoning 2012;53(2):118–45.
40.Han DQ,Han CZ,Yang Y.A modified evidence combination approach based on ambiguity measure.2008 11th international conference on information fusion(FUSION);2008 June 30–July 3;Cologne,Germany.Piscataway,NJ:IEEE Press;2008.p.1–6.
41.Han DQ,Deng Y,Han CZ,Hou ZQ.Weighted evidence combination based on distance of evidence and uncertainty measure.J Infrared Millimeter Waves 2011;30(5):396–400.
42.Bian ZQ,Zhang XG.Patternre cognition.2nded.Beijing:Tsinghua University Press;2000,p.178–84(Chinese).
43.Masson MH,Denoeux T.ECM:An evidential version of the fuzzy c-means algorithm.Pattern Recogn 2008;41(4):1384–97.
44.Smarandache F,Martin A,Osswald C.Contradiction measures and specificity degrees of basic belief assignments.2011 14th international conference on information fusion(FUSION).2011 June 5–8;Chicago,IL,USA.Piscataway,NJ:IEEE Press;2011.p.1–8.
45.Smarandache F,Han D,Martin A.Comparative study of contradiction measures in the theory of belief functions.2012 15th international conference on information fusion(FUSION);2012 July 9–12;Singapore.Piscataway,NJ:IEEE Press;2012.p.271–7.
46.Yang Y,Han DQ.A new distance-based total uncertainty measure in the theory of belief functions.Knowledge-Based Syst 2016;94:114–23.
Yang Yireceived the M.S.and Ph.D.degrees in control science and engineering from Xi'an Jiaotong University in 2005 and 2010 respectively,and then became a teacher there.Her main research interests are evidence theory,image processing and information fusion.
Han Deqiangis an associate professor and Ph.D.supervisor at School of Electronic and Information Engineering,Xi'an Jiaotong University,China.He received the Ph.D.degree from the Xi'an Jiaotong University in 2008.His current research interests are evidence theory,pattern classification and information fusion.
Jean Dezertreceived the electrical engineering degree from the école Franc?aise de Radioélectricité électronique et Informatique(EFREI),Paris,in 1985,the D.E.A.degree in 1986 from the University Paris VII(Jussieu),and his Ph.D.degree from the University Paris XI,Orsay,in 1990,all in Automatic Control and Signal Processing.Since 1993,he has been a Senior Research Scientist in the Information and Fusion Systems Research Unit,Information and Modeling and Processing Department(DTIM),ONERA.His current research interests include autonomous navigation,estimation theory,stochastic systems theory and its applications to multisensor-multitarget tracking(MS-MTT),information fusion and plausible reasoning.He has served as Local Arrangements Organizer for the 2000 3rd International Conference on Information Fusion(Fusion)in Paris,a Secretary for ISIF in 2001,an Executive Vice-President for ISIF in 2004,and President for ISIF in 2016.He has been involved in the Technical Program Committee of Fusion 2001–2015 International Conferences.He was a Board Member of the International Society of Information Fusion.He gave several invited plenary talks and seminars on information fusion in Europe,America,Australia and China during latest years.
31 July 2015;revised 1 February 2016;accepted 22 February 2016
Available online 10 May 2016
Belief interval;
Evidence theory;
Imprecision;
Non-specificity;
Uncertainty
?2016 Chinese Society of Aeronautics and Astronautics.Production and hosting by Elsevier Ltd.This is an open access article under the CCBY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).
*Corresponding author.Tel.:+86 29 82667971.
E-mail address:deqhan@mail.xjtu.edu.cn(D.Han).
Peer review under responsibility of Editorial Committee of CJA.
 CHINESE JOURNAL OF AERONAUTICS2016年3期
CHINESE JOURNAL OF AERONAUTICS2016年3期
- CHINESE JOURNAL OF AERONAUTICS的其它文章
- Optimization on cooperative feed strategy for radial–axial ring rolling process of Inco718 alloy by RSM and FEM
- Prediction of cutting forces in ball-end milling of 2.5D C/C composites
- Performance optimization of grooved slippers for aero hydraulic pumps
- Modeling of reliability and performance assessment of a dissimilar redundancy actuation system with failure monitoring
- Motion synchronization in a dual redundant HA/EHA system by using a hybrid integrated intelligent control design
- Remaining useful life prediction based on the Wiener process for an aviation axial piston pump
