Theory on Structure and Coloring of Maximal Planar Graphs(1)Recursion Formulae of Chromatic Polynomial and Four-Color Conjecture
XU Jin
?
Theory on Structure and Coloring of Maximal Planar Graphs(1)Recursion Formulae of Chromatic Polynomial and Four-Color Conjecture
XU Jin*
(School of Electronics Engineering and Computer Science, Peking University, Beijing 100871, China)(Key Laboratory of High Confidence Software Technologies, Peking University, Beijing 100871, China)
In this paper, two recursion formulae of chromatic polynomial of a maximal planar graphare obtained: when, letbe a 4-wheel ofwith wheel-centerand wheel-cycle, then; when, leta 5-wheel ofwith wheel-centerand wheel-cycle, then,,, where“”denotes the operation of vertex contraction. Moreover, the application of the above formulae to the proof of Four-Color Conjecture is investigated. By using these formulae, the proof of Four-Color Conjecture boils down to the study on a special class of graphs, viz., 4-chromatic-funnel pseudo uniquely-4-colorable maximal planar graphs.
Four-Color Conjecture; Maximal planar graphs; Chromatic polynomial; Pseudo uniquely-4-colorable planar graphs; 4-chromatic-funnel
1 Introduction
All graphs considered in this paper are finite, simple, and undirected. For a given graph, we use,,, andto denote the vertex set, the edge set, the degree of, and the neighborhood ofin(the set of neighbors of), respectively, which can be written as,,, andfor short. The order ofis the number of its vertices. A graphis a subgraph ofifand. For a subgraphof, wheneverare adjacent in, they are also adjacent in, thenis an induced subgraph ofor a subgraph ofinduced by, denoted by. Two graphsandare disjoint if they have no vertex in common. By starting with a disjoint union ofand, and adding edges joining every vertex ofto every vertex of, one obtains the join ofand, denoted by. We writeandfor the complete graph and cycle of order, respectively. The joinof a cycle and a single vertex is referred to as a wheel, denoted by(the examplesare shown in Fig. 1, whereis called the cycle ofand the vertex ofis called the center of. If, we also denote the cycle ofby. A graph is-regular if all of its vertices have the same degree. A 3-regular graph is usually called a cubic graph.
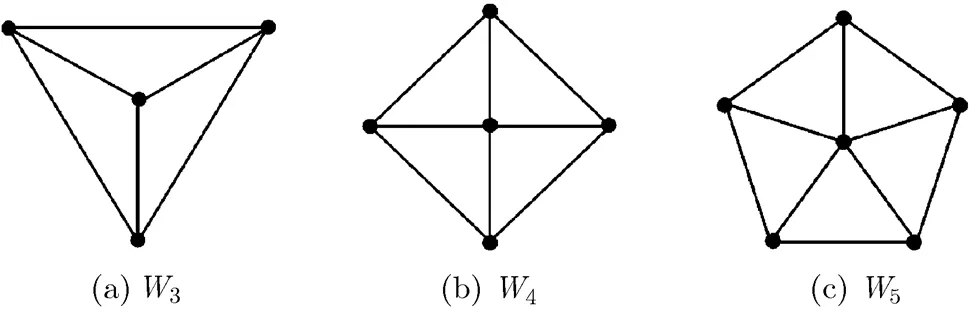
Fig. 1 Three wheels
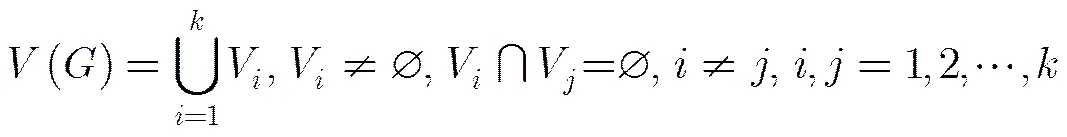
A graph is said to be planar if it can be drawn in the plane so that its edges intersect only at their ends. Such a drawing is called a planar embedding of the graph. Any planar graph considered in the paper is under its planar embedding. A maximal planar graph is a planar graph to which no new edges can be added without violating planarity. A triangulation is a planar graph in which every face is bounded by three edges (including its infinite face). It can be easily proved that maximal planar graphs are triangulations, and vice versa.
The planar graph is a very important class of graphs no matter which aspect, theoretical or practical, is concerned. In theory, there are many famous conjectures that have very significant effect on graph theory, even mathematics, such as the Four-Color Conjecture, the Uniquely Four- Colorable Planar Graphs Conjecture, the Nine- Color Conjecture, Three-Color Problem,[1]. In application, planar graphs can be directly applied to the study of layout problems[2], information science[3],.
Because the studying object of the well-known Four-Color Conjecture can be confined to maximal planar graphs, many scholars have been strongly attracted to the study of this typical topic. They did research on maximal planar graphs from a number of different standpoints, such as degree sequence, construction, coloring, traversability, generating operations,[4]. Moreover, many new conjectures on maximal planar graphs have been proposed, for instance, Uniquely Four-Colorable Planar Graphs Conjecture and Nine-Color Conjecture. These conjectures have gradually become the essential topics on maximal planar graphs.
In the process of studying Four-Color Conjecture, one important method, finding an unavoidable set of reducible configurations, was proposed. This method has been used in Kempe’s “proof”[5], Heawood’s counterexample[6], and the computer-assisted proof due to Appel and Haken. Using this method, Appel and Haken found an unavoidable set containing 1936 reducible configurations and proved Four-Color Conjecture. In 1997, Robertson,.[10,11]gave a simplified proof. They found an unavoidable set containing only 633 reducible configurations.
The research on unavoidable sets originated from Wernicke’s work[12]in 1904. The concept of reducibility was introduced by Birkhoff[13]in 1913. On the research for finding an unavoidable set of reducible configurations, the great contribution was made by German mathematician Heesch[14]. He introduced a method “discharging” to find an unavoidable set of a maximal planar graph, which lied the foundation for solving Four-Color Conjecture by electronic computer in 1976. Moreover, many researchers studied Four-Color Problem by this method, such as Franklin[15,16], Reynolds[17], Winn[18], Ore and Stemple[19], and Mayer[20].
However, these proofs were all computer- assisted and hard to be checked one by one by hand. Therefore, finding a mathematical method to concisely solve the Four-Color Problem is still an open hard problem.
Another incorrect proof of Four-Color problem[21]was given by Tait in 1880. His proof was based on an assumption: each 3-connected cubic plane graph was Hamiltonian. Because this assumption is incorrect, Tait’s proof is incorrect. Although the error in his proof was found by Petersen[22]in 1898, the counterexample was not given until 1946[23]. Then, in 1968, Grinberg[24]obtained a necessary condition, thus producing many non-Hamiltonian cubic planar graphs of 3-connected. Although the proof of Tait was incorrect, his work had a strong influence on the research on Graph Theory, especially edge-coloring theory.
In order to calculate the chromatic polynomial of a given graph, the basic tool is the Deletion- Contract Edge Formula.
The Deletion-contract Edge Formula. For a given graphand an edge, we have
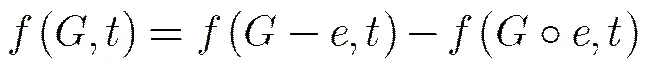
Moreover, XU etal.[32,33]obtained a recursion formula of chromatic polynomial by vertex deletion and a chromatic polynomial between a graph and its complement.
Perhaps for the perfect degree of Tutte’s work and his highly status in academia, once upon a time, it was thought that to attack the Four-Color Problem by chromatic polynomial is impossible. Nevertheless, our work below gives a new hope to solve the Four-Color Problem by chromatic polynomial.
2 Recursion Formulae of Chromatic Polynomial by Contracting Wheels
We first give two useful lemmas as follows.
Lemma 1[26]For any planar graph, it is 4-colorable if and only if
Lemma 2[25,27]Letbe the union of two subgraphsand, whose intersection is a complete graph of order. Then
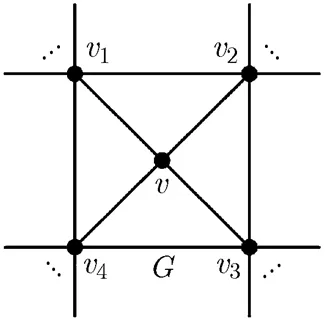
Fig. 2 A maximal planar graph with a 4-degree vertex
Proof In the following derivation, we representby. Now we first compute the chromatic polynomial of the graphby the Deletion-Contract Edge Formula. For the sake of understanding clearly, a method introduced by Zykov[34]is used here, where the chromatic polynomials are represented by the corresponding graphical graphs without. Notice that if there are at least two edges adjacent to two vertices, then only one remains and others are deleted excluding.
By Lemma 2, the chromatic polynomial of the first subgraph in Formula (4) is. Therefore,
Notice that the two graphs in Formula (6) denoteand, respectively. It is easily proved that they are both maximal planar graphs of order. Thus, we obtain that
namely
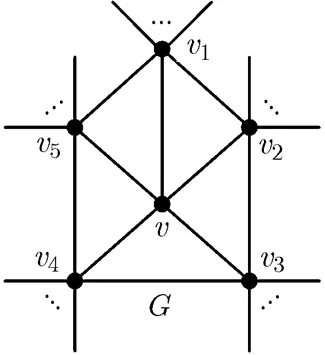
Fig. 3 A maximal planar graph with a 5-degree vertex
By Lemma 2, the chromatic polynomial of the first graph in Formula (10) is. Therefore, we can obtain that
Notice that the fourth graph in Formula (12), denoted by, contains a subgraph, and so. Thus, we can obtain that
Actually, the first graph in the first bracket of Formula (13) is; the first graph in the second bracket is; and the first graph in the third bracket is. The proof is completed.
3 Two Mathematical Ideas for Attacking Four-Color Conjecture Based on Theorem 2
It is well-known that mathematical induction is an effective method to prove Four-Color Conjecture, in which maximal planar graphs are classified into three cases by their minimum degrees. The case of minimum degree 3 or 4 is easy to prove by induction, but for the case of minimum degree 5 no mathematical method has been found. Based on Theorems 1 and 2, we give a new method to prove Four-Color Conjecture as follows.
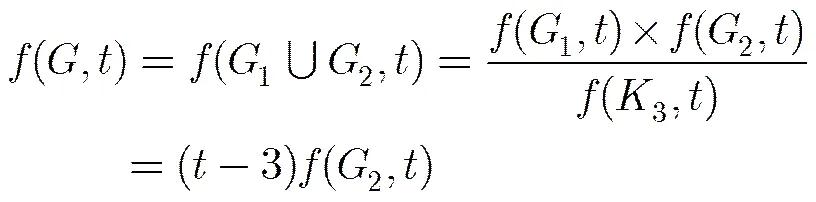
By the induction hypothesis,. Thus,.
Hence, the result is true when.
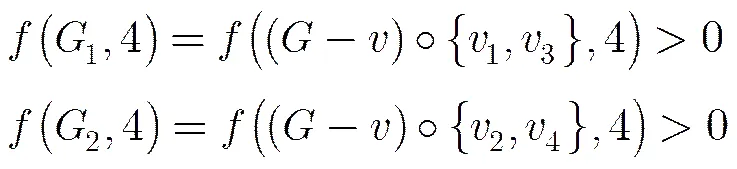
The key ingredient of the proof is the following Case 3.
The maximal planar graph of minimum degree 5 with fewest vertices is the icosahedron, depicted in Fig. 4(a), which has 12 vertices. Obviously, the icosahedron is 4-colorable. There is no maximal planar graph of minimum degree 5 with 13 vertices. Notice that for any maximal planar graphof order at least 14 and minimum degree 5, there exists a vertexsuch thatand, where(see Fig. 3). Hence, the graphin Theorem 2 is a 4-colorable maximal planar graph of minimum degree at least 4. Based on this evidence, we give two mathematical ideas to proveas follows.
The first idea is based on the fact that the value of each square bracket in Formula (9) is no less than zero. Hence, the Four-Color Conjecture can be proved if any square bracket’s value is greater than zero. The value of the first square bracket is greater than zero if and only if there existssuch thator. Therefore,if and only if each square bracket in Formula (9) is equal to zero. Moreover, the value of the first square bracket is zero if and only if for any,and, that is, for any, the colors of vertices of the funnel shown in Fig. 4(b) are pairwise different. Such maximal planar graphs are called 4-chromatic-funnel pseudo uniquely-4-colorable maximal planar graphs. For instance, each graph in Fig. 5 is a 4-chromatic- funnel pseudo-uniquely 4-colorable maximal planar graph.
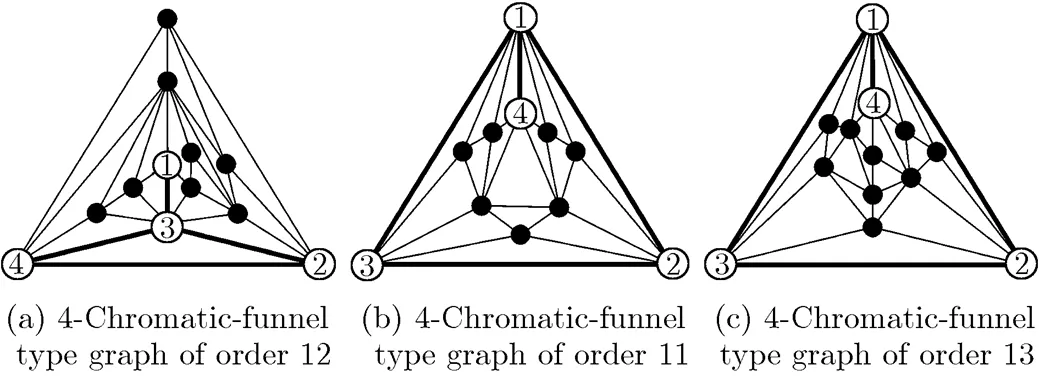
Fig. 5 Three 4-chromatic-funnel pseudo uniquely-
4-colorable maximal planar graphs
Now we give the second idea to prove. The maximal planar graphs,, andin Theorem 2 can be regarded as the graphs obtained fromby deleting a 5-degree vertexand contracting,, andinto a single vertex, respectively (see Fig. 6). Moreover, the 5-cycle consisting of the neighbors ofinis contracted to a funnel subgraphin,in, andin, respectively, where,, andare the new vertices obtained by contractingandrespectively.

Fig. 6 The processes of generating the three funnel subgraphs
By the induction hypothesis,,, andare 4-colorable. In order to prove, it is needed to prove that at least one of the funnel subgraphs,, andis not 4-chromatic.
Therefore, the second idea is to prove that for any maximal planar graphof minimum degree 5, there exists a 5-wheelinsuch that at least one of the funnel subgraphs,, andcorresponding to,, andis not a 4- chromatic-funnel. For instance, the graph in Fig. 5(a) can be regarded as the maximal planar graph obtained from the graph in Fig. 7 by the operation shown in Fig. 6. It is not difficult to prove that the other two graphs obtained from Fig. 7 by the operation shown in Fig. 6 have no 4-chromatic- funnel.
4 Conclusion
In this paper, we give two recursion formulae of chromatic polynomial on maximal planar graphs. Based on these formulae, we find: (1) two mathematical ideas for attacking Four-Color Conjecture; (2) a method to generate maximal planar graphs, called contracting and extending operational system, which establishes a relation between the structure and colorings of a maximal planar graph. For instance, the maximal planar graph in Fig. 5(a) can be obtained from the graph in Fig. 7 by the extending 5-wheel operation, in other words, the maximal planar graph in Fig. 7 can be obtained from the graph in Fig. 5(a) by the contracting 5-wheel operation. A detailed research on contracting and extending operational system of maximal planar graphs will be given in later articles.
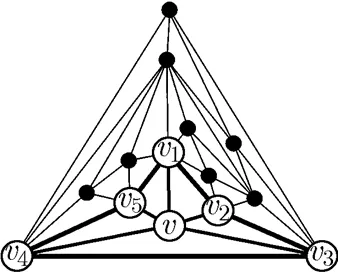
Fig. 7 A maximal planar graph that can be contracted to the graph in Fig. 5(a)

